高斯牛顿法和LM算法异同示例
LM(Levenberg-Marquardt)算法和高斯牛顿(Gauss-Newton)算法是两种用于非线性最小二乘问题的优化算法,它们也有一些相似之处:
-
迭代优化:LM算法和高斯牛顿算法都使用迭代的方式来优化参数值,以逐步减小拟合残差。
-
非线性拟合:这两种算法都适用于非线性函数的拟合任务,在拟合参数化模型与观测数据之间的差异时表现出良好的效果。
-
基于梯度的优化:高斯牛顿算法和LM算法都利用了目标函数的梯度信息。高斯牛顿算法使用一阶导数(Jacobian矩阵)来近似目标函数,而LM算法在梯度下降方向上引入了一个调节因子。
-
局部搜索:这两种算法都是局部搜索方法,即在每次迭代中更新参数值以接近局部最优解。
虽然LM算法和高斯牛顿算法在实现细节和收敛性质上存在差异,但它们都属于非线性最小二乘优化问题的常用方法,并且共享一些相似的思想和原理。
LM(Levenberg-Marquardt)算法和高斯牛顿(Gauss-Newton)算法都是用于非线性最小二乘问题的优化算法,它们在计算方式和收敛性质上存在一些区别。
-
计算方式:
- 高斯牛顿算法通过迭代地线性近似非线性函数,将非线性最小二乘问题转化为一系列线性最小二乘子问题。每次迭代,通过求解线性系统来更新参数值。
- LM算法则结合了高斯牛顿算法和梯度下降算法的思想。在每次迭代中,LM算法通过权衡高斯牛顿算法和梯度下降算法的更新步长,以更好地适应不同情况下的问题。
-
收敛性质:
- 高斯牛顿算法在参数空间中可能收敛到局部极小值,因为它依赖于二阶导数信息,而二阶导数矩阵的正定性不一定成立。
- LM算法通过引入一个调节因子(也称为阻尼因子),使得在接近极小值时能够更好地探索参数空间。这样的机制可以提供更好的全局收敛性,并且对初始参数的选择不太敏感。
总结起来,高斯牛顿算法是一种更简单和更快速的迭代方法,但可能收敛到局部极小值。而LM算法则更加复杂一些,在计算上稍微耗时,但具有更好的全局收敛性能。在实际应用中,可以根据问题的特点选择适合的优化算法。
以下是使用C++实现高斯牛顿法对一组数据进行拟合的示例代码:
#include <iostream>
#include <Eigen/Dense>using namespace Eigen;// 高斯函数模型
double gaussian(double x, double a, double b, double c) {return a * exp(-(x - b) * (x - b) / (2 * c * c));
}// 高斯牛顿拟合算法
void fitGaussian(const VectorXd& xData, const VectorXd& yData, double& a, double& b, double& c) {int n = xData.size();int m = 3; // 参数个数MatrixXd J(n, m); // 雅可比矩阵VectorXd residual(n); // 残差向量VectorXd delta(m); // 参数增量向量// 设定初始参数值a = 1.0;b = 0.0;c = 1.0;// 设置最大迭代次数和收敛阈值int maxIter = 100;double epsilon = 1e-6;for (int iter = 0; iter < maxIter; ++iter) {// 构造雅可比矩阵和残差向量for (int i = 0; i < n; ++i) {double xi = xData(i);double residual_i = yData(i) - gaussian(xi, a, b, c);J(i, 0) = -residual_i / a;J(i, 1) = residual_i * (xi - b) / (c * c);J(i, 2) = residual_i * (xi - b) * (xi - b) / (c * c * c);residual(i) = residual_i;}// 计算参数增量delta = (J.transpose() * J).inverse() * J.transpose() * residual;// 更新参数估计值a += delta(0);b += delta(1);c += delta(2);// 判断是否收敛if (delta.norm() < epsilon)break;}
}int main() {// 原始数据VectorXd xData(10);VectorXd yData(10);xData << 1, 2, 3, 4, 5, 6, 7, 8, 9, 10;yData << 0.98, 1.89, 3.02, 4.15, 4.97, 6.05, 6.92, 8.01, 8.94, 10.02;// 拟合参数double a, b, c;fitGaussian(xData, yData, a, b, c);// 输出拟合结果std::cout << "Fitted parameters:\n";std::cout << "a = " << a << "\n";std::cout << "b = " << b << "\n";std::cout << "c = " << c << "\n";return 0;
}
输出:1 3 2
在这个示例中,我们定义了一个高斯函数gaussian()用于描述高斯函数模型。fitGaussian()函数实现了高斯牛顿拟合算法,其中根据雅可比矩阵和残差计算参数增量,并根据增量更新参数估计值。主函数中给出了一组原始数据,然后调用fitGaussian()函数进行拟合。最后,输出拟合结果。
需要注意的是,这只是一个简单的示例,实际应用中可能需要根据具体情况来选择合适的模型和参数优化算。
以下是使用Levenberg-Marquardt (LM) 算法进行高斯函数拟合的示例代码:
#include <iostream>
#include <Eigen/Dense>
#include <unsupported/Eigen/LevenbergMarquardt>using namespace Eigen;// 高斯函数模型
struct GaussianModel {template<typename T>bool operator()(const T* const x, T* residual) const {T a = params[0];T b = params[1];T c = params[2];residual[0] = y - a * exp(-(x[0] - b) * (x[0] - b) / (2 * c * c));return true;}double y;Vector3d params;
};// 高斯牛顿拟合算法
void fitGaussian(const VectorXd& xData, const VectorXd& yData, double& a, double& b, double& c) {int n = xData.size();Vector3d params;params << 1.0, 0.0, 1.0; // 初始参数值// 定义 LM 算法参数NumericalDiff<GaussianModel> numericalDiff;LevenbergMarquardt<NumericalDiff<GaussianModel>> lm(numericalDiff);lm.parameters.maxfev = 100; // 最大迭代次数lm.parameters.xtol = 1e-6; // 收敛阈值// 构造问题并求解GaussianModel model;model.params = params;for (int i = 0; i < n; ++i) {model.y = yData(i);VectorXd x(1);x << xData(i);lm.minimize(x, model);params = model.params;}// 更新拟合结果a = params[0];b = params[1];c = params[2];
}int main() {// 原始数据VectorXd xData(10);VectorXd yData(10);xData << 1, 2, 3, 4, 5, 6, 7, 8, 9, 10;yData << 0.98, 1.89, 3.02, 4.15, 4.97, 6.05, 6.92, 8.01, 8.94, 10.02;// 拟合参数double a, b, c;fitGaussian(xData, yData, a, b, c);// 输出拟合结果std::cout << "Fitted parameters:\n";std::cout << "a = " << a << "\n";std::cout << "b = " << b << "\n";std::cout << "c = " << c << "\n";return 0;
}
在这个示例中,我们使用了Eigen库中的LevenbergMarquardt类来实现LM算法。首先定义了一个GaussianModel结构体,其中重载了括号运算符,该运算符计算残差并返回给LM算法。然后,在fitGaussian()函数中,构造了一个LevenbergMarquardt对象并设置了最大迭代次数和收敛阈值。接下来,使用该对象对每个数据点进行拟合,并更新参数估计值。最后输出拟合结果。
请注意,为了使用LM算法,需要在代码中添加Eigen库的相关头文件,并使用命令`-I /path
相关文章:

高斯牛顿法和LM算法异同示例
LM(Levenberg-Marquardt)算法和高斯牛顿(Gauss-Newton)算法是两种用于非线性最小二乘问题的优化算法,它们也有一些相似之处: 迭代优化:LM算法和高斯牛顿算法都使用迭代的方式来优化参数值&#…...

奥威BI财务数据分析方案:只做老板想看的
奥威BI财务数据分析方案是一套从老板的视角出发,做老板想看的财务数据分析报表,帮助老板更好地了解公司的财务状况和经营绩效的综合性智能财务数据分析方案,可实现财务数据分析可视化、灵活自主性,随时为老板提供最为直观的财务数…...

opencv进阶19-基于opencv 决策树cv::ml::DTrees 实现demo示例
opencv 中创建决策树 cv::ml::DTrees类表示单个决策树或决策树集合,它是RTrees和 Boost的基类。 CART是二叉树,可用于分类或回归。对于分类,每个叶子节点都 标有类标签,多个叶子节点可能具有相同的标签。对于回归,每…...

Unity通过TCP/IP协议进行通信
uinty项目中需要与C编写的硬件进行通信,因此采用TCP/IP协议进行通信,主要实现了与服务器的连接、通信内容的发送以及断开连接等功能。 根据确定好的协议格式,编写需要发送的内容,将其转为字节流(byte[])通过…...

基于VuePress搭建知识库
我这边需要搭建一个运维知识库,将项目的方方面面记录下来,方便新手接手运维。 准备环境 Nginx 1.19.0VuePress 1.xMinio RELEASE.2022-02-16T00-35-27Zvuepress-theme-vdoing主题 安装VuePress 根据官网步骤即可 # 创建目录 mkdir vuepress-starter…...

odoo安装启动遇到的问题
问题:在第一次加载odoo配置文件的时候,启动失败 方法: 1、先检查odoo.conf的内容,尤其是路径 [options] ; This is the password that allows database operations: ; admin_passwd admin db_host 127.0.0.1 db_port 5432 d…...
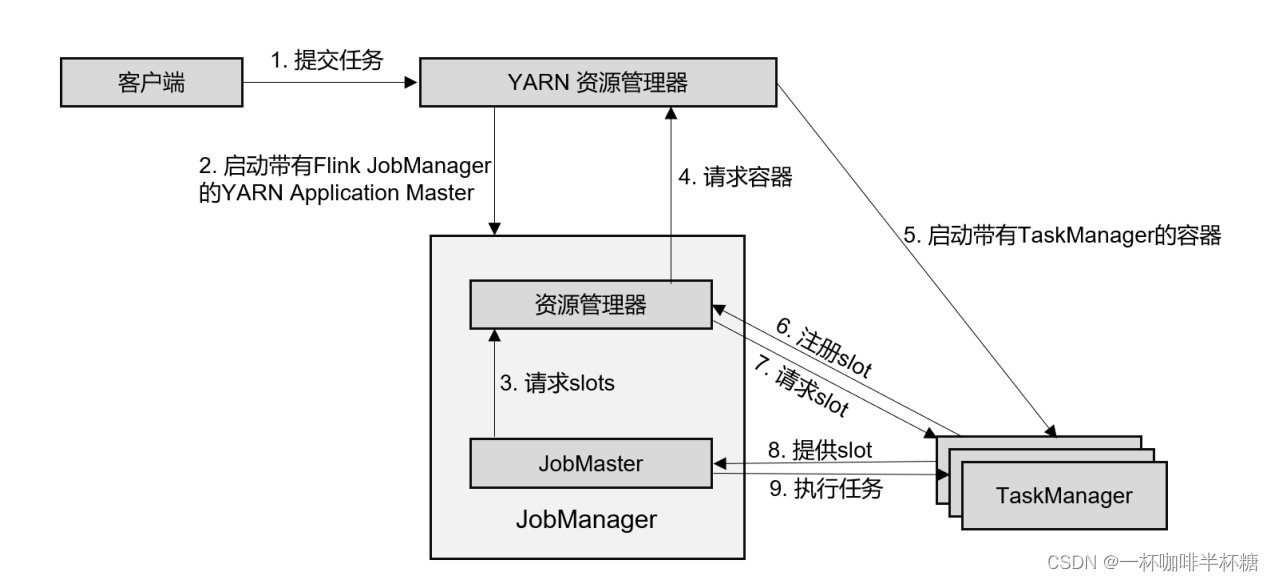
【Flink】Flink提交流程
我们通常在学习的时候需要掌握大数据组件的原理以便更好的掌握这个大数据组件,Flink实际生产开发过程中最常见的就是提交到yarn上进行调度,模式使用的Per-Job模式,下面我们就给大家讲下Flink提交Per-Job任务到yarn上的流程,流程图…...

哪种英特尔实感设备适合您?
原文链接 https://www.intelrealsense.com/which-device-is-right-for-you/ 无论您是深度和跟踪硬件的新手,还是经验丰富的专业人士,确定我们提供的众多英特尔实感产品中哪些产品适合您的项目仍然是一项挑战。在这篇文章中,我们将讨论英特尔…...

C++11的四种强制类型转换
目录 语法格式 static_cast(静态转换) dynamic_cast(动态转换) const_cast(常量转换) reinterpret_cast(重解释) 语法格式 cast-name <typename> (expression) 其中cast-name为static_cast、dynamic_cast、const_cast 和 reinterpret_cast之一…...
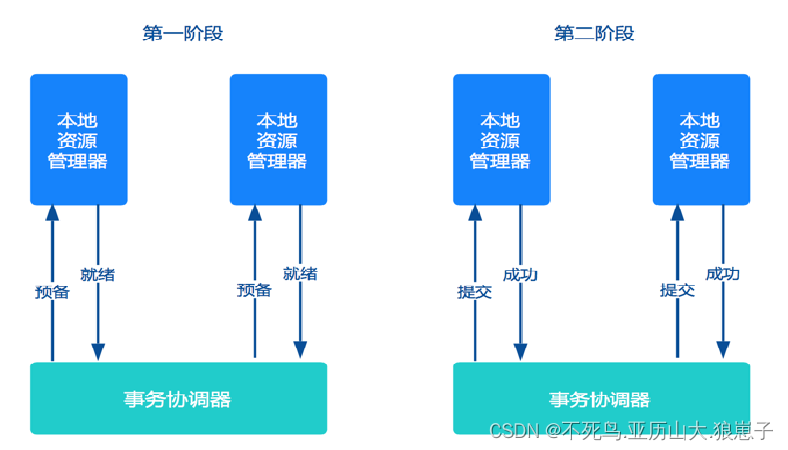
分布式事务(4):两阶段提交协议与三阶段提交区别
1 两阶段提交协议 两阶段提交方案应用非常广泛,几乎所有商业OLTP数据库都支持XA协议。但是两阶段提交方案锁定资源时间长,对性能影响很大,基本不适合解决微服务事务问题。 缺点: 如果协调者宕机,参与者没有协调者指…...
------ 实现多节点渲染【修改beginWork和completeWork】)
React源码解析18(9)------ 实现多节点渲染【修改beginWork和completeWork】
摘要 目前,我们已经实现了单节点的,beginWork,completeWork,diff流程。但是对于多节点的情况,比如: <div><span></span><span></span> </div>这种情况,我们还没有处…...

【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
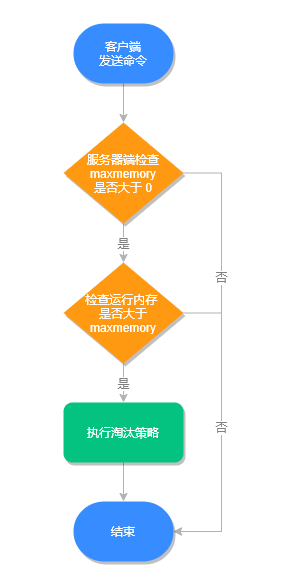
Redis 缓存满了怎么办?
引言 Redis 缓存使用内存来保存数据,随着需要缓存的数据量越来越大,有限的缓存空间不可避免地会被写满。此时,应该怎么办?本篇文章接下来就来聊聊缓存满了之后的数据淘汰机制。 值得注意的是,在 Redis 中 过期策略 和…...
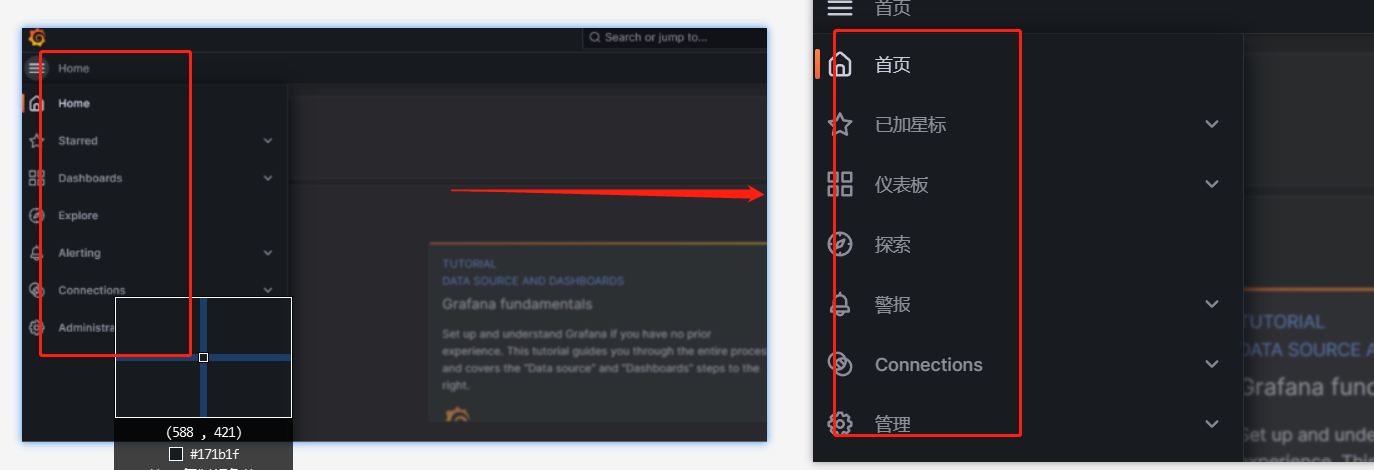
Grafana 安装配置教程
Grafana 安装配置教程 一、介绍二、Grafana 安装及配置2.1 下载2.2 安装2.2.1 windows安装 - 图形界面2.2.2 linux安装 - 安装脚本 三、Grafana的基本配置3.1 登录3.2 Grafana设置中文 四、grafana基本使用 一、介绍 Grafana是一个通用的可视化工具。对于Grafana而言࿰…...

【Linux】临界资源和临界区
目录 一、临界资源 二、如何实现对临界资源的互斥访问 1、互斥量 2、信号量 3、临界区 三、临界区 四、进程进入临界区的调度原则 一、临界资源 概念:临界资源是一次仅允许一个进程使用的共享资源,如全局变量等。 二、如何实现对临界资源的互斥访问 …...

拓扑排序Topological sorting/DFS C++应用例题P1113 杂务
拓扑排序 拓扑排序可以对DFS的基础上做变更从而达到想要的排序效果。因此,我们需要xy准备,vis数组记录访问状态,每一个任务都可以在dfs的过程中完成。 在使用拓扑排序方法时一些规定: 通常使用一个零时栈不会直接输出排序的节点…...
基于jenkins构建生成CICD环境
目录 一、安装配置jenkins 1、环境配置 2、软件要求 3、jdk安装(我是最小化安装,UI自带java要先删除rm -rf /usr/local/java 4、安装jenkins-2.419-1.1 二、Jenkins配置 1、修改jenkins初始密码 2、安装 Jenkins 必要插件 3、安装 Publish Over SS…...
在线图片怎么转换成PDF?在线图片转换成PDF步骤介绍
文件格式要转化不知道怎么办?想要网上下载文件格式转换软件,但是却不知道下载哪个好?今天小编小编就给大家分享一下靠谱的小圆象PDF转换器工具,想知道这款软件好不好用?在线图片怎么转换成PDF?那就进来看看吧。 在线图片怎么转换成PDF 小圆象PDF转换…...
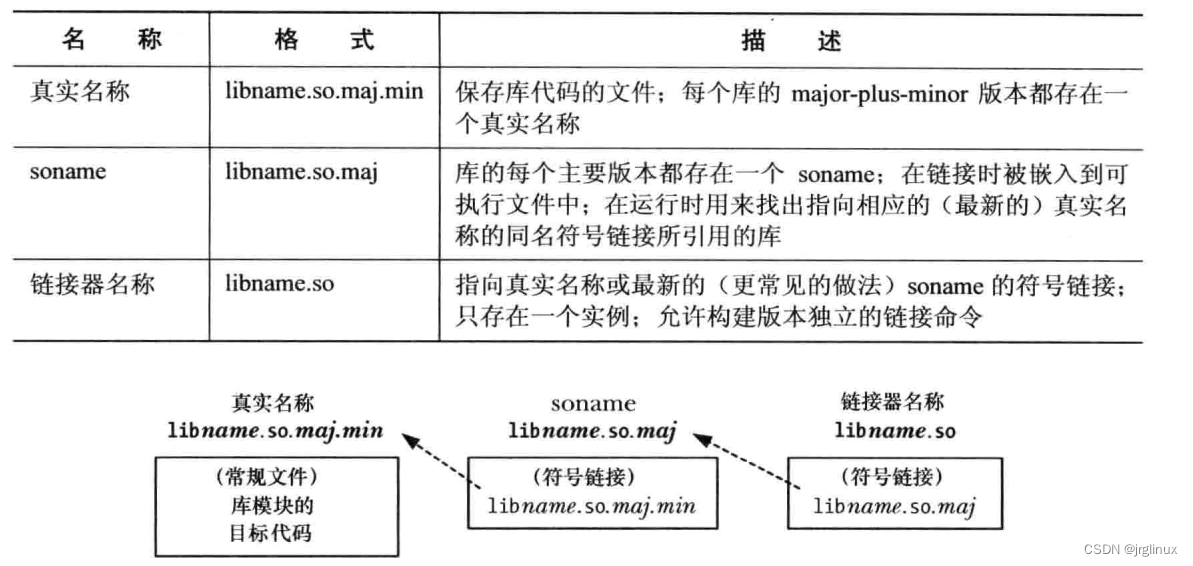
Linux共享库基础及实例
共享库是将库函数打包成一个可执行文件,使得其在运行时可以被多个进程共享。 目标库 回顾下构建程序的一种方式: 将每个源文件编译成目标文件,再通过链接器将这些目标文件链接组成一个可执行程序。 gcc -g -c prog.c mod1.c mod2.c gcc -g …...

java八股文面试[java基础]——final 关键字作用
为什么局部内部类和匿名内部类只能访问final变量: 知识来源 【基础】final_哔哩哔哩_bilibili...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
