代码随想录算法训练营day43 | LeetCode 1049. 最后一块石头的重量 II 494. 目标和 474. 一和零
1049. 最后一块石头的重量 II(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:把全部石头重量加起来,然后除以二,就等于背包的最大容量。然后就可以按照背包问题做,再将石头总质量减去背包最大容量得到的差减去背包里面的值,就是可以得到的最小结果。
int lastStoneWeightII(vector<int>& stones) {int sum = accumulate(stones.begin(), stones.end(), 0);int target = sum/2;vector<int> dp(target+1, 0);for(int i=0; i<stones.size(); i++){for(int j=target; j>=stones[i]; j--){dp[j] = max(dp[j], dp[j-stones[i]]+stones[i]);}}return (sum - dp[target]) - dp[target];
}494. 目标和(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:乍一看还以为是个排列组合题目,想用回溯法来做,但是结果会超时。所以还是用dp做,关键在于dp的构造,细想其实可以得到这个式子:left-right=targt, left+right=sum,可以推出left=(sum+target)/2,这就好办了,left即为我们的背包最大容量。dp[left]即为我们要求的最终结果。(但此题与其他不同的是,他不是每次都去比较拿最大值,而是一直做加法,我的理解是实际还是做的排列组合)
int findTargetSumWays(vector<int>& nums, int target) {int sum = accumulate(nums.begin(), nums.end(), 0);if((sum+target)%2==1) return 0;if(abs(target)>sum) return 0;int bagSize = (target+sum)/2;vector<int> dp(bagSize+1, 0);dp[0] = 1;for(int i=0; i<nums.size(); i++){for(int j=bagSize; j>=nums[i]; j--){dp[j] += dp[j-nums[i]];}}return dp[bagSize];
}474. 一和零(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:可以看作是两个背包合一起,要装一起装,要不都不装。
int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1, 0));for(string str : strs){int zeroNum=0, oneNum=0;for(char ch : str){if(ch=='0') zeroNum++;else oneNum++;}for(int i=m; i>=zeroNum; i--){for(int j=n; j>=oneNum; j--){dp[i][j] = max(dp[i][j], dp[i-zeroNum][j-oneNum] + 1);}}}return dp[m][n];
}相关文章:

代码随想录算法训练营day43 | LeetCode 1049. 最后一块石头的重量 II 494. 目标和 474. 一和零
1049. 最后一块石头的重量 II(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台) 思路:把全部石头重量加起来,然后除以二,就等于背包的最大容量。然后就可以按照背包问题…...
Linux安装jdk、mysql、并部署Springboot项目
😜作 者:是江迪呀✒️本文关键词:Linux、环境安装、JDK安装、MySQL、MySQL安装☀️每日 一言:知行合一! 文章目录 一、前言二、安装步骤2.1 安装JDK(1)创建文件夹(便于后…...
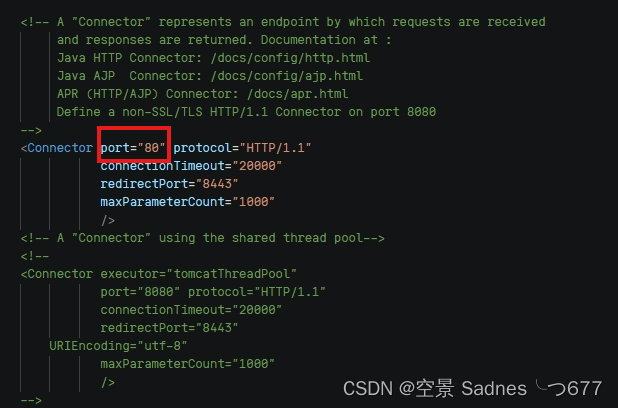
tomcat更改端口号和隐藏端口号
因为默认端口:8080不会自动隐藏,因此为了更显格调需要将其改为:80 进入tomcat的server文件 将其改为80,之后将tomcat重新启动即可 tomcat启动流程 [rootshang ~]# cd /usr/local/tomcat/apache-tomcat-8.5.92 [rootshang apache-tomcat-8.5.92]# cd b…...

生信分析Python实战练习 2 | 视频19
开源生信 Python教程 生信专用简明 Python 文字和视频教程 源码在:https://github.com/Tong-Chen/Bioinfo_course_python 目录 背景介绍 编程开篇为什么学习Python如何安装Python如何运行Python命令和脚本使用什么编辑器写Python脚本Python程序事例Python基本语法 数…...

wps设置其中几页为横版
问题:写文档的时候,有些表格列数太多,页面纵向显示内容不完整,可以给它改成横向显示。 将鼠标放在表格上一页的底部,点击‘插入-分页-下一页分节符’。 将鼠标放在表格页面的底部,点击‘插入-分页-下一页分…...

如何在Ubuntu 22.04上安装PHP 8.1并设置本地开发环境
引言 PHP是一种流行的服务器脚本语言,用于创建动态和交互式web页面。开始使用你选择的语言是学习编程的第一步。 本教程将指导您在Ubuntu上安装PHP 8.1,并通过命令行设置本地编程环境。您还将安装依赖管理器Composer,并通过运行脚本来测试您…...
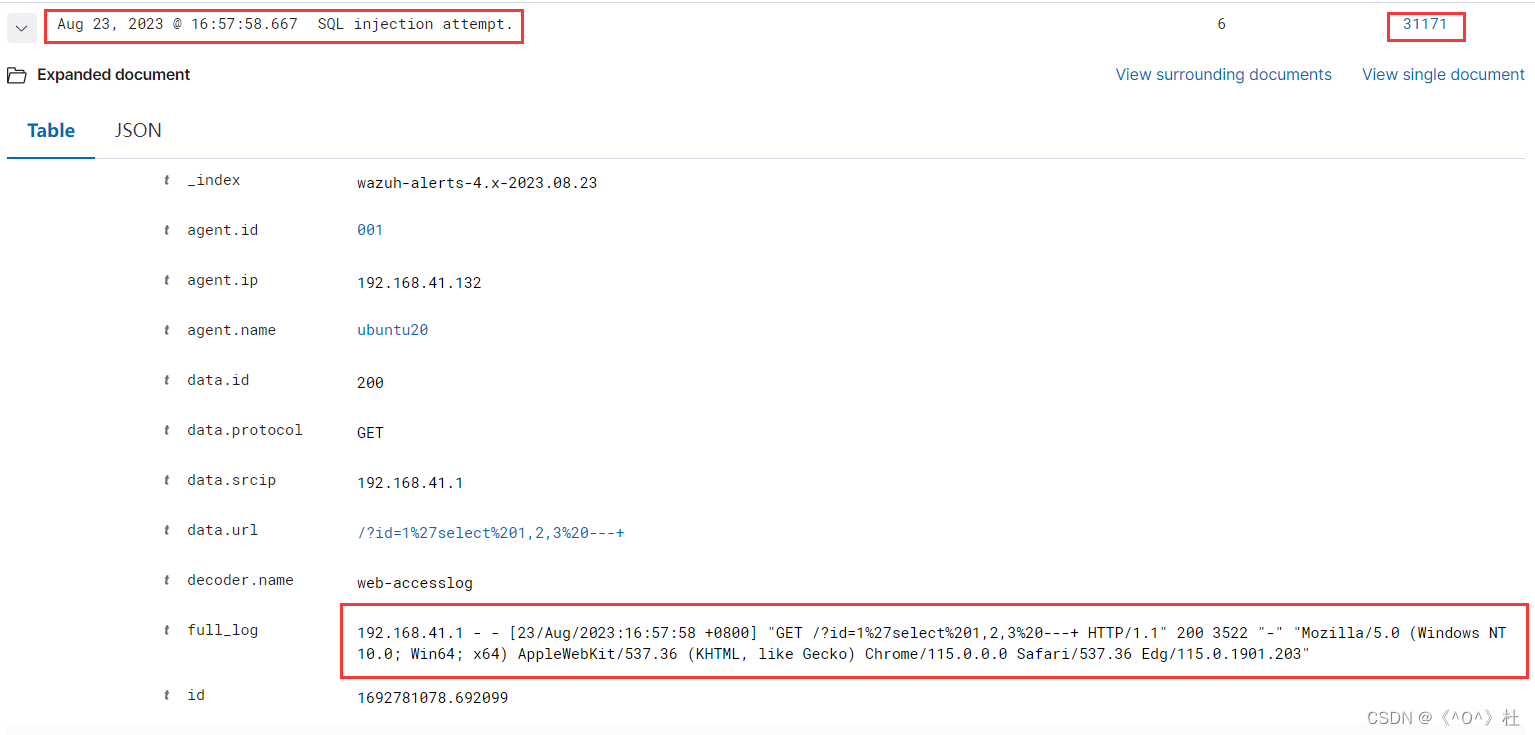
wazuh安装与使用
目录 一、wazuh安装 二、wazuh使用 一、wazuh安装 下载:https://wazuh.com 可以直接安装OVA这个,然后导入到Linux中就可以使用了。 导入完毕后开启,使用远程连接工具进行连接,出现以下画面则成功了。 之后可以看一下图形化界面…...

Vue 3 常见面试题汇总
前端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 前言 最近两年许多大厂都在实行“降本增效”、“优化组织架构”,然后“为社会输送了大量人才”,今年(2023ÿ…...
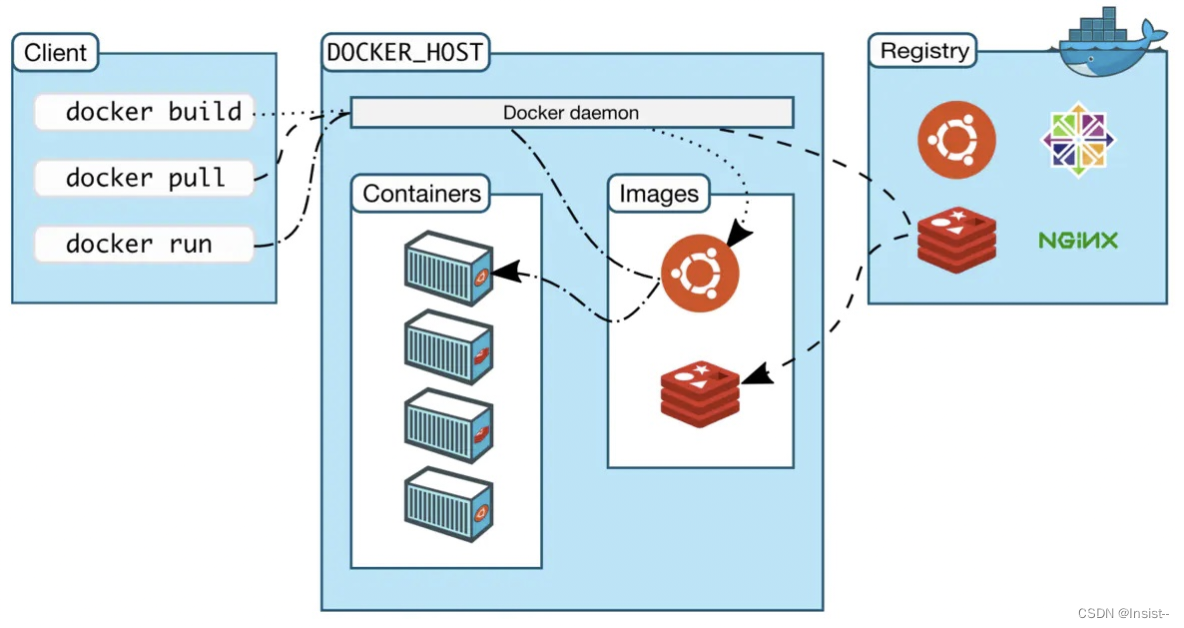
Docker是什么?详谈它的框架、使用场景、优势
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 目录 一、什么是 Docker? 二、Docker 的架构 1、Docker客户端 2、Docker守护进程 3、Docker镜像 4、Docker容器 5、Docker…...
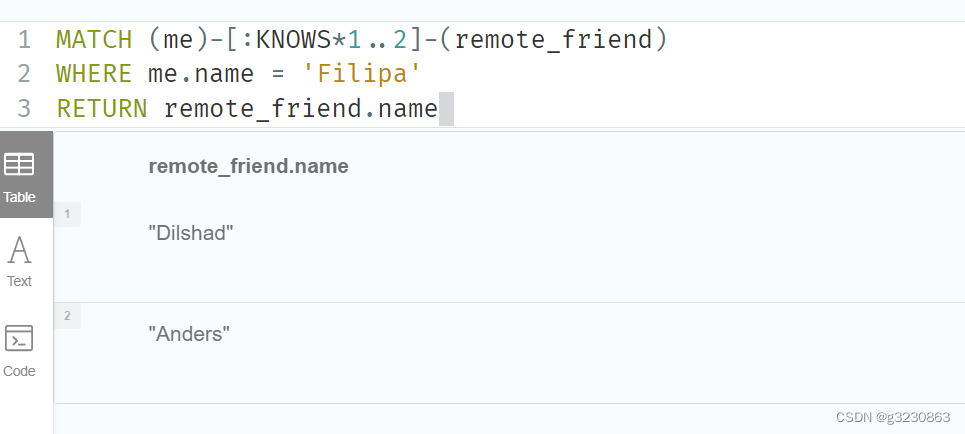
neo4j
UNWIND 将列表里的值展开 CREATE (N0:Person {name: Anders}) CREATE (N1:Person {name: Becky}) CREATE (N2:Person {name: Cesar}) CREATE (N3:Person {name: Dilshad}) CREATE (N4:Person {name: George}) CREATE (N5:Person {name: Filipa})CREATE (N0)-[:KNOWS]->(N3)…...
4.16 TCP通信实现(客户端))
【项目 计网5】 4.15 TCP通信实现(服务器端)4.16 TCP通信实现(客户端)
文章目录 4.15 TCP通信实现(服务器端)4.16 TCP通信实现(客户端) 4.15 TCP通信实现(服务器端) // TCP 通信的服务器端// TCP 通信的服务器端 #include <stdio.h> #include <arpa/inet.h> #incl…...
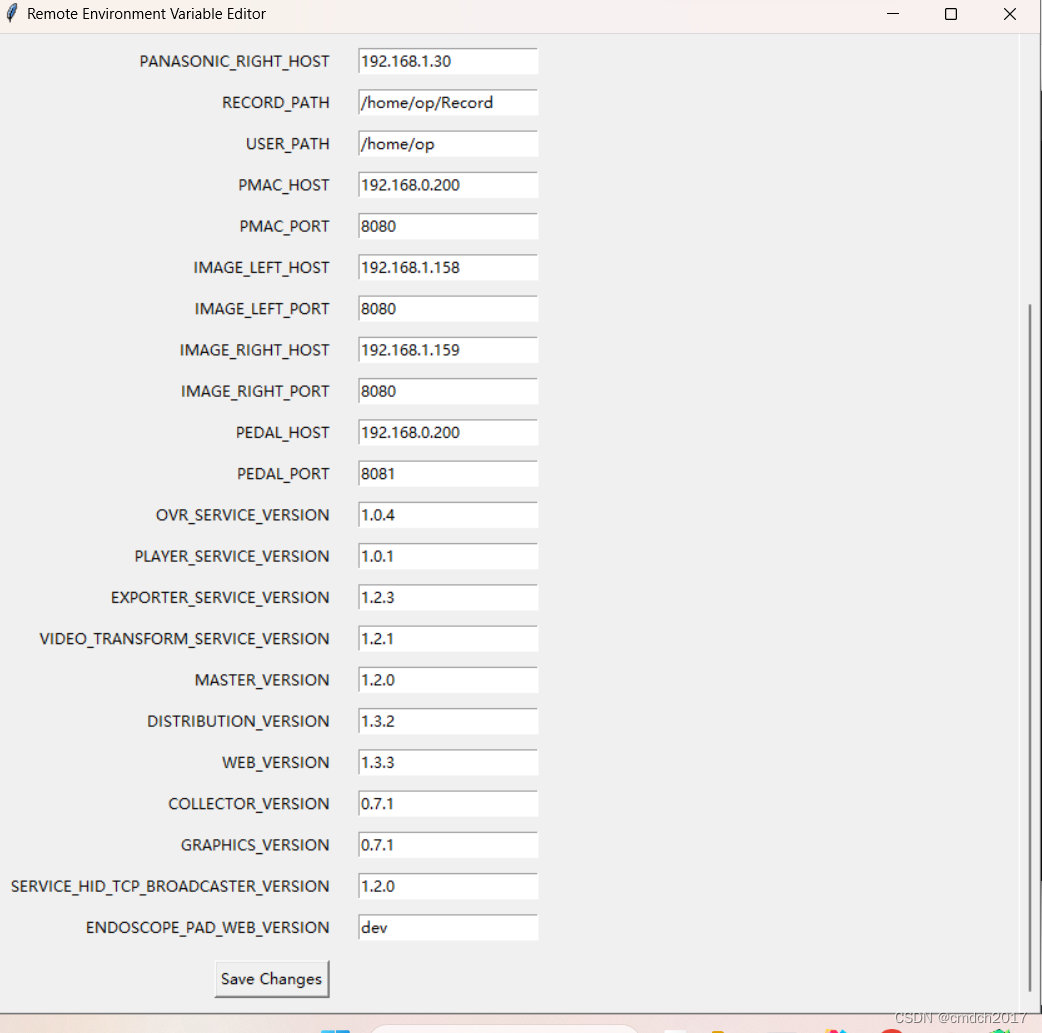
windows可视化界面管理服务器上的env文件
需求:在 Windows 环境中通过可视化界面编辑位于 Linux 主机上的 env 文件的情况,我现在环境是windows环境,我的env文件在linux的192.168.20.124上,用户是op,密码是op,文件绝对路径是/home/op/compose/env …...

自然语言处理在智能客服和聊天机器人中的应用
文章目录 1. 引言2. NLP基础2.1 词法分析2.2 语法分析2.3 语义理解2.4 情感分析 3. 智能客服中的应用3.1 自动问答3.2 意图识别3.3 情感分析与情绪识别 4. 聊天机器人中的应用4.1 对话生成4.2 上下文理解 5. 技术原理与挑战5.1 语言模型5.2 数据质量和多样性5.3 上下文理解 6. …...
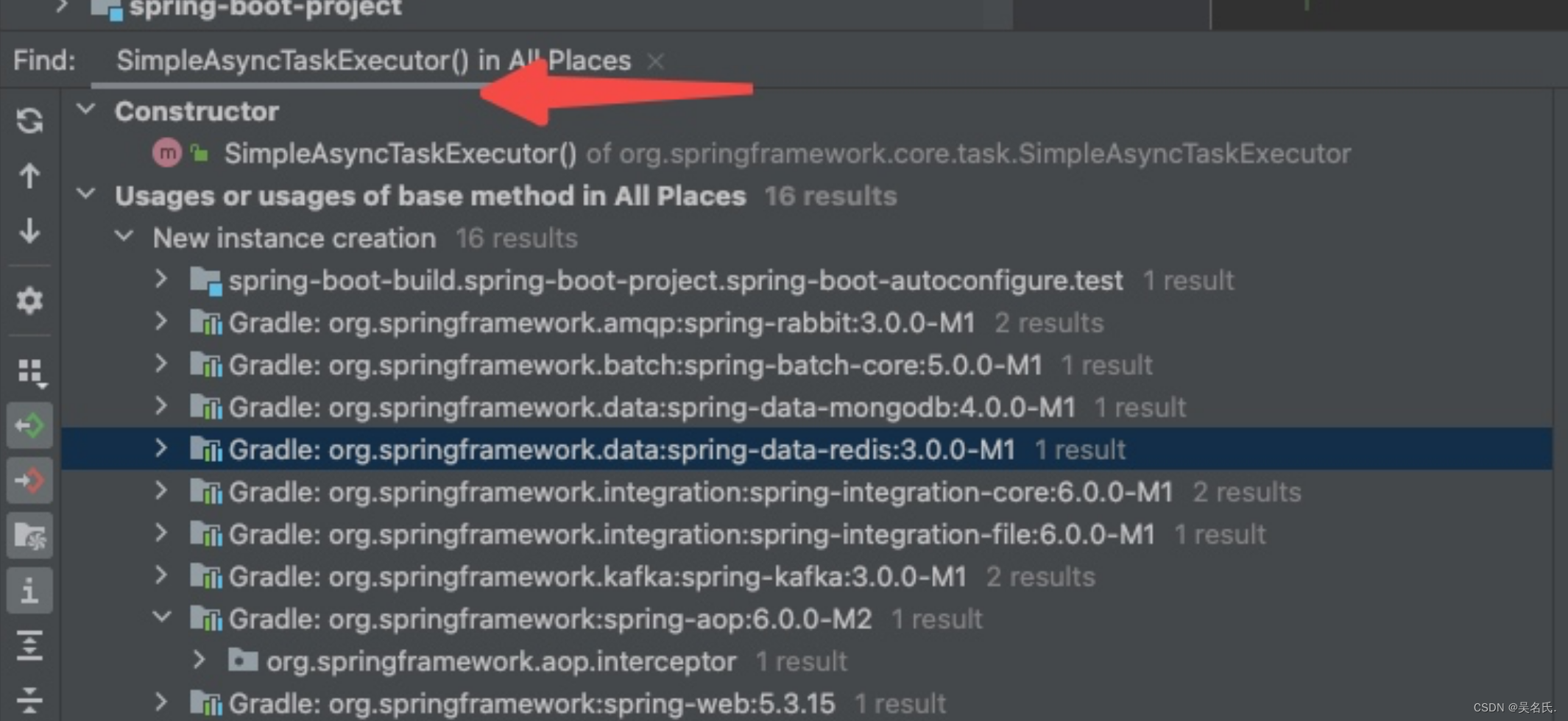
为什么不建议使用@Async注解创建线程
1 前言 在很久很久之前,我有一段痛苦的记忆。那种被故障所驱使的感觉,在我脑海里久久无法驱散。 原因无它,有小伙伴开启了线程池的暴力使用模式。没错,就是下面这篇文章。 夺命故障 ! 炸出了投资人! 我有必要简单的…...

更新Ubuntu18.04上的CUDA和GCC
问题: 有一台服务器的GPU是1080,有八张卡,已经好久没有人用了。cuda版本是10.1,我现在拿来复现一些论文的模型,经常遇到版本依赖问题,报错Driver is too old。所以要更新一下驱动。遇到的主要问题是gcc版本也太低了&am…...
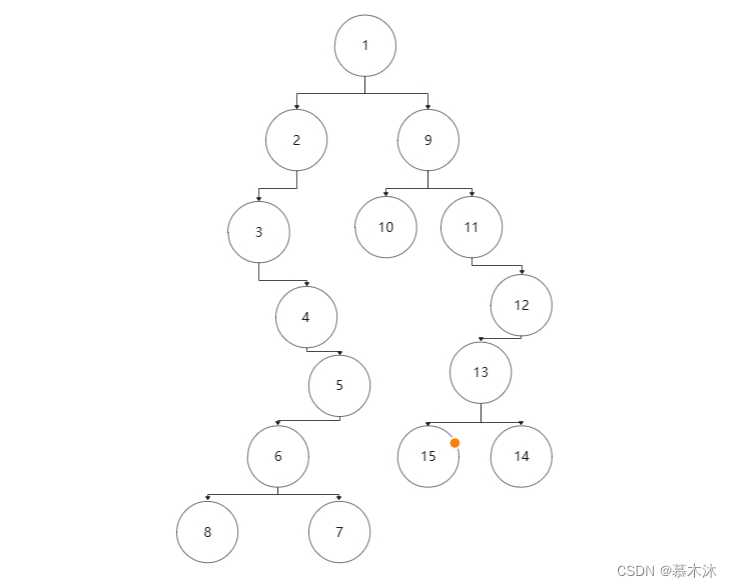
算法通过村第6关【青铜】| 如何通过中序和后序遍历恢复二叉树
中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1 通过这两个遍历顺序恢复二叉树 首先我们知道中序遍历顺序左中右,后序遍历顺序左右中 第一步: 由后序遍历确定根结点为1 > 由中序遍历…...

高斯牛顿法和LM算法异同示例
LM(Levenberg-Marquardt)算法和高斯牛顿(Gauss-Newton)算法是两种用于非线性最小二乘问题的优化算法,它们也有一些相似之处: 迭代优化:LM算法和高斯牛顿算法都使用迭代的方式来优化参数值&#…...

奥威BI财务数据分析方案:只做老板想看的
奥威BI财务数据分析方案是一套从老板的视角出发,做老板想看的财务数据分析报表,帮助老板更好地了解公司的财务状况和经营绩效的综合性智能财务数据分析方案,可实现财务数据分析可视化、灵活自主性,随时为老板提供最为直观的财务数…...

opencv进阶19-基于opencv 决策树cv::ml::DTrees 实现demo示例
opencv 中创建决策树 cv::ml::DTrees类表示单个决策树或决策树集合,它是RTrees和 Boost的基类。 CART是二叉树,可用于分类或回归。对于分类,每个叶子节点都 标有类标签,多个叶子节点可能具有相同的标签。对于回归,每…...

Unity通过TCP/IP协议进行通信
uinty项目中需要与C编写的硬件进行通信,因此采用TCP/IP协议进行通信,主要实现了与服务器的连接、通信内容的发送以及断开连接等功能。 根据确定好的协议格式,编写需要发送的内容,将其转为字节流(byte[])通过…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
