Docker是什么?详谈它的框架、使用场景、优势
作者:Insist--
个人主页:insist--个人主页
作者会持续更新网络知识和python基础知识,期待你的关注
目录
一、什么是 Docker?
二、Docker 的架构
1、Docker客户端
2、Docker守护进程
3、Docker镜像
4、Docker容器
5、Docker注册中心
三、Docker 的使用场景
1、开发
2、测试
3、部署
4、云
四、Docker 的优势
1、轻量级
2、可移植性
3、自动化部署
4、可扩展性
5、安全性
前言
Docker 的出现,让开发、测试和部署应用程序变得更加简单和高效。在本文中,我们将深入探讨 Docker 的概念、架构、使用场景以及优势。

一、什么是 Docker?
Docker 是一种开源的容器化技术,它使得开发、测试和部署应用程序变得更加简单和高效。 Docker 利用 Linux 内核的容器化技术(即 cgroups 和 namespace)来创建、部署和管理应用程序。这些容器可以在任何 Docker 环境中可预测地运行,无论是开发环境还是生产环境。
二、Docker 的架构
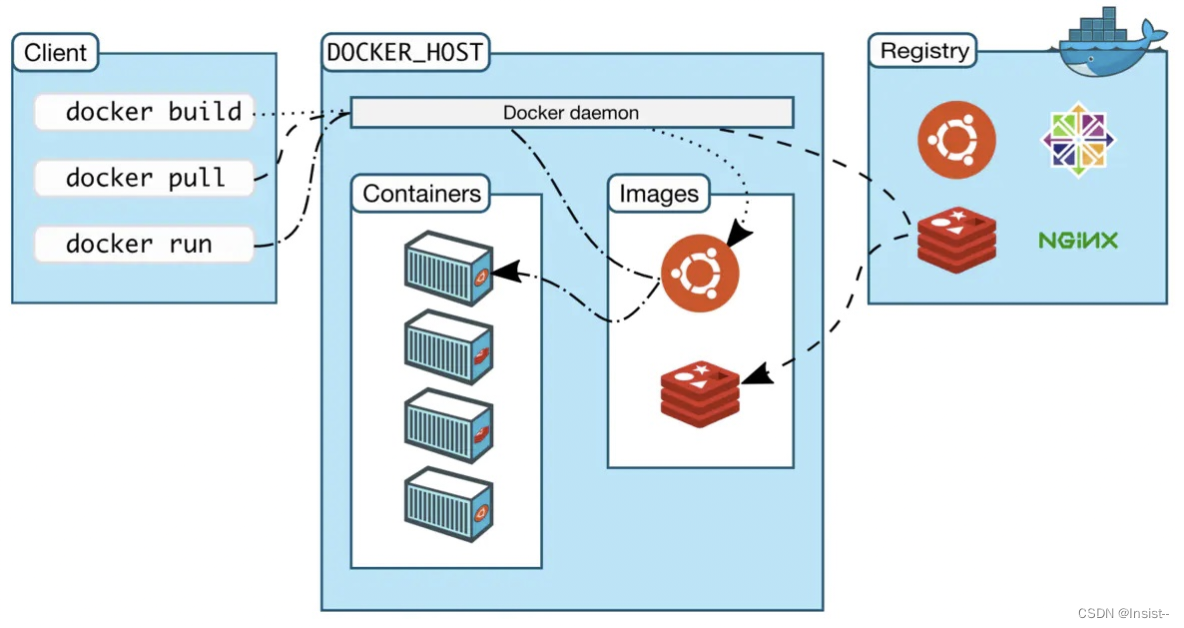
Docker的框架包括以下几个主要组成部分:
1、Docker客户端
提供给用户和开发者使用的命令行工具,可以通过API和Docker守护进程通信。用户可以使用docker命令来发出各种请求,例如docker images(列出所有的镜像),docker run(启动一个新的容器)等等。
2、Docker守护进程
是Docker架构中最重要的组件之一,负责管理Docker容器、镜像、网络等。Docker守护进程是一个长时间运行的进程,通过监听Docker客户端的请求并响应来工作。
3、Docker镜像
是Docker应用程序的构建块,是一个轻量级、可移植的打包格式。一个Docker镜像包含了一个完整的可运行环境,包括代码、运行时、库文件、环境变量等。
4、Docker容器
是Docker的核心概念之一,是由Docker镜像创建而来的一个运行实例。Docker容器是轻量级的,可以在几毫秒内启动和停止,可以实现快速部署和扩展。
5、Docker注册中心
是用来存储和管理Docker镜像的中央仓库。Docker Hub是一个公共的Docker注册中心,用户可以在这里分享和下载Docker镜像。
三、Docker 的使用场景
Docker 可以用于各种场景,比如说:
1、开发
Docker 可以使开发人员在不同的开发环境中快速地部署和测试应用程序。
2、测试
Docker 可以创建一致的环境,使得在任何地方都可以进行相同的测试。
3、部署
Docker 可以使部署变得更加简单和一致,因为它可以自动地处理应用程序的依赖项和配置。
4、云
Docker 可以使云提供商更加灵活,因为它可以在不同的云环境中轻松地部署和管理应用程序。
四、Docker 的优势
1、轻量级
Docker容器非常轻量级,可以快速地启动和停止,这使得它们在处理大量并发请求或需要快速部署和停运时非常有用。
2、可移植性
Docker可以使应用程序在不同的平台上可预测地运行,这使得跨平台开发和部署变得更加容易。例如 开发人员可以在本地使用Docker容器进行开发和测试,然后将其部署到云平台上。
3、自动化部署
Docker可以自动处理应用程序的依赖项和配置,这使得部署更加简单和一致。使用Docker,可以轻松地管理和更新应用程序的多个版本,而不会出现复杂的部署问题。
4、可扩展性
Docker可以轻松地扩展应用程序的性能,因为它可以自动地创建和停止容器。这使得在需要时增加或减少应用程序的容量变得非常容易,从而满足用户的需求。
5、安全性
Docker利用Linux的容器化技术来隔离应用程序,使得应用程序更加安全。另外,Docker还提供了其他安全特性,例如 加密和认证,以确保只有授权用户可以访问容器化的应用程序。更加安全。
相关文章:

Docker是什么?详谈它的框架、使用场景、优势
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 目录 一、什么是 Docker? 二、Docker 的架构 1、Docker客户端 2、Docker守护进程 3、Docker镜像 4、Docker容器 5、Docker…...
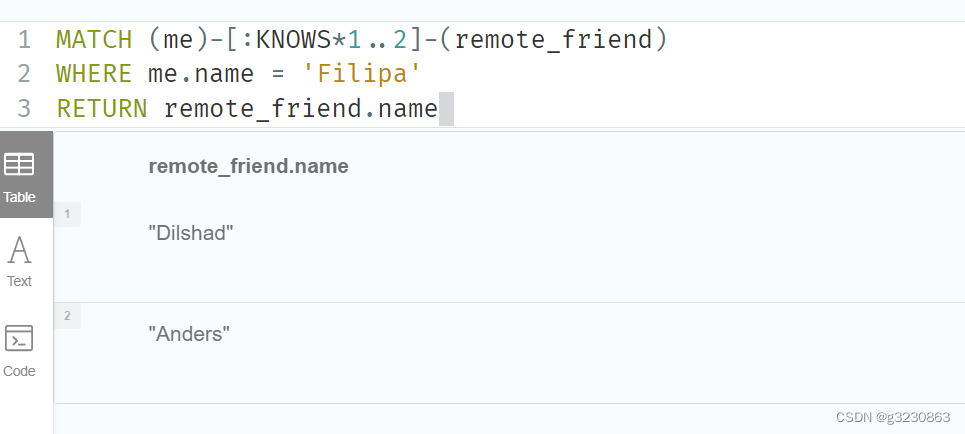
neo4j
UNWIND 将列表里的值展开 CREATE (N0:Person {name: Anders}) CREATE (N1:Person {name: Becky}) CREATE (N2:Person {name: Cesar}) CREATE (N3:Person {name: Dilshad}) CREATE (N4:Person {name: George}) CREATE (N5:Person {name: Filipa})CREATE (N0)-[:KNOWS]->(N3)…...
4.16 TCP通信实现(客户端))
【项目 计网5】 4.15 TCP通信实现(服务器端)4.16 TCP通信实现(客户端)
文章目录 4.15 TCP通信实现(服务器端)4.16 TCP通信实现(客户端) 4.15 TCP通信实现(服务器端) // TCP 通信的服务器端// TCP 通信的服务器端 #include <stdio.h> #include <arpa/inet.h> #incl…...
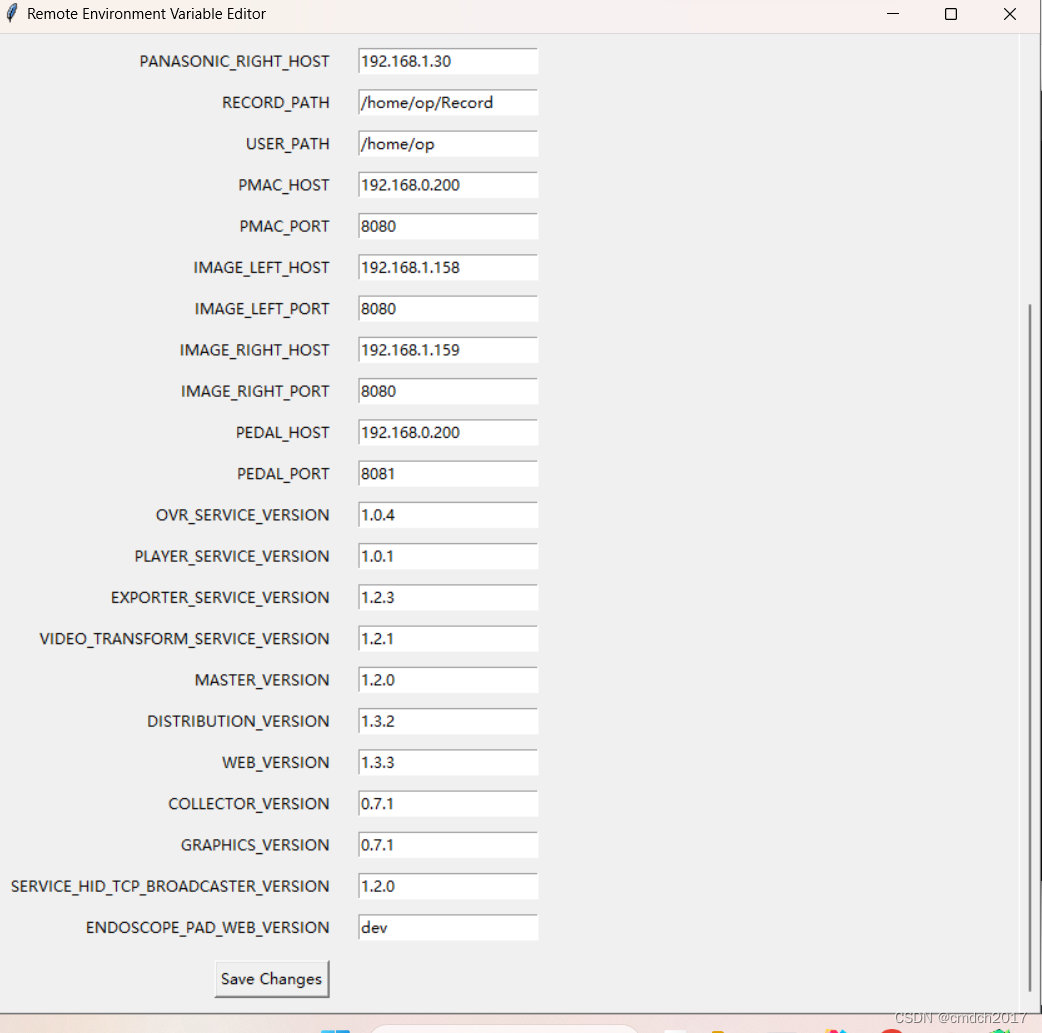
windows可视化界面管理服务器上的env文件
需求:在 Windows 环境中通过可视化界面编辑位于 Linux 主机上的 env 文件的情况,我现在环境是windows环境,我的env文件在linux的192.168.20.124上,用户是op,密码是op,文件绝对路径是/home/op/compose/env …...

自然语言处理在智能客服和聊天机器人中的应用
文章目录 1. 引言2. NLP基础2.1 词法分析2.2 语法分析2.3 语义理解2.4 情感分析 3. 智能客服中的应用3.1 自动问答3.2 意图识别3.3 情感分析与情绪识别 4. 聊天机器人中的应用4.1 对话生成4.2 上下文理解 5. 技术原理与挑战5.1 语言模型5.2 数据质量和多样性5.3 上下文理解 6. …...
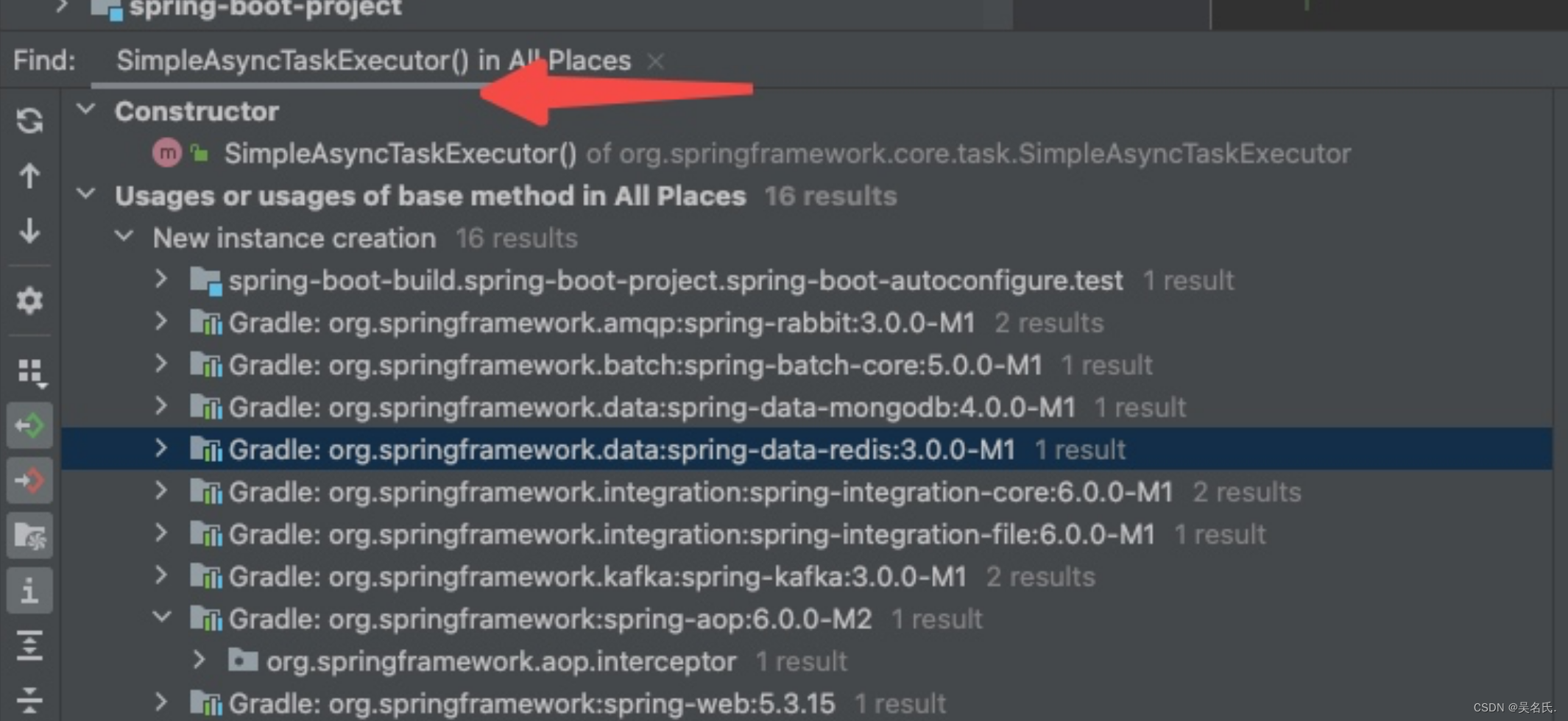
为什么不建议使用@Async注解创建线程
1 前言 在很久很久之前,我有一段痛苦的记忆。那种被故障所驱使的感觉,在我脑海里久久无法驱散。 原因无它,有小伙伴开启了线程池的暴力使用模式。没错,就是下面这篇文章。 夺命故障 ! 炸出了投资人! 我有必要简单的…...

更新Ubuntu18.04上的CUDA和GCC
问题: 有一台服务器的GPU是1080,有八张卡,已经好久没有人用了。cuda版本是10.1,我现在拿来复现一些论文的模型,经常遇到版本依赖问题,报错Driver is too old。所以要更新一下驱动。遇到的主要问题是gcc版本也太低了&am…...
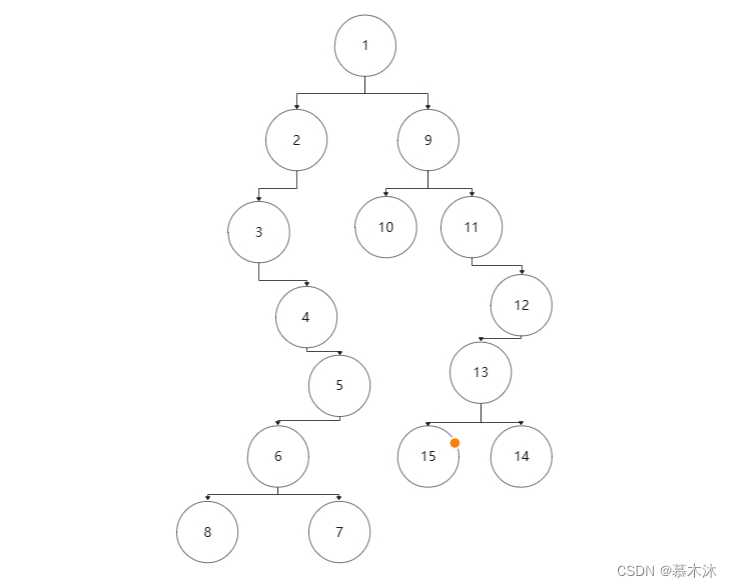
算法通过村第6关【青铜】| 如何通过中序和后序遍历恢复二叉树
中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1 通过这两个遍历顺序恢复二叉树 首先我们知道中序遍历顺序左中右,后序遍历顺序左右中 第一步: 由后序遍历确定根结点为1 > 由中序遍历…...

高斯牛顿法和LM算法异同示例
LM(Levenberg-Marquardt)算法和高斯牛顿(Gauss-Newton)算法是两种用于非线性最小二乘问题的优化算法,它们也有一些相似之处: 迭代优化:LM算法和高斯牛顿算法都使用迭代的方式来优化参数值&#…...

奥威BI财务数据分析方案:只做老板想看的
奥威BI财务数据分析方案是一套从老板的视角出发,做老板想看的财务数据分析报表,帮助老板更好地了解公司的财务状况和经营绩效的综合性智能财务数据分析方案,可实现财务数据分析可视化、灵活自主性,随时为老板提供最为直观的财务数…...

opencv进阶19-基于opencv 决策树cv::ml::DTrees 实现demo示例
opencv 中创建决策树 cv::ml::DTrees类表示单个决策树或决策树集合,它是RTrees和 Boost的基类。 CART是二叉树,可用于分类或回归。对于分类,每个叶子节点都 标有类标签,多个叶子节点可能具有相同的标签。对于回归,每…...

Unity通过TCP/IP协议进行通信
uinty项目中需要与C编写的硬件进行通信,因此采用TCP/IP协议进行通信,主要实现了与服务器的连接、通信内容的发送以及断开连接等功能。 根据确定好的协议格式,编写需要发送的内容,将其转为字节流(byte[])通过…...

基于VuePress搭建知识库
我这边需要搭建一个运维知识库,将项目的方方面面记录下来,方便新手接手运维。 准备环境 Nginx 1.19.0VuePress 1.xMinio RELEASE.2022-02-16T00-35-27Zvuepress-theme-vdoing主题 安装VuePress 根据官网步骤即可 # 创建目录 mkdir vuepress-starter…...

odoo安装启动遇到的问题
问题:在第一次加载odoo配置文件的时候,启动失败 方法: 1、先检查odoo.conf的内容,尤其是路径 [options] ; This is the password that allows database operations: ; admin_passwd admin db_host 127.0.0.1 db_port 5432 d…...
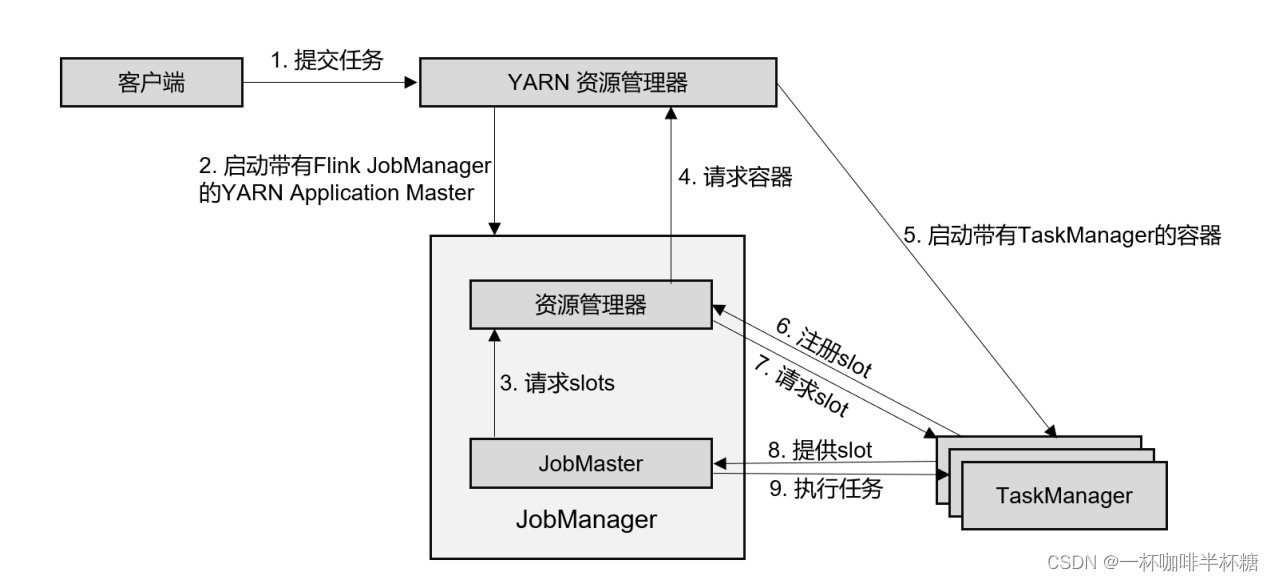
【Flink】Flink提交流程
我们通常在学习的时候需要掌握大数据组件的原理以便更好的掌握这个大数据组件,Flink实际生产开发过程中最常见的就是提交到yarn上进行调度,模式使用的Per-Job模式,下面我们就给大家讲下Flink提交Per-Job任务到yarn上的流程,流程图…...

哪种英特尔实感设备适合您?
原文链接 https://www.intelrealsense.com/which-device-is-right-for-you/ 无论您是深度和跟踪硬件的新手,还是经验丰富的专业人士,确定我们提供的众多英特尔实感产品中哪些产品适合您的项目仍然是一项挑战。在这篇文章中,我们将讨论英特尔…...

C++11的四种强制类型转换
目录 语法格式 static_cast(静态转换) dynamic_cast(动态转换) const_cast(常量转换) reinterpret_cast(重解释) 语法格式 cast-name <typename> (expression) 其中cast-name为static_cast、dynamic_cast、const_cast 和 reinterpret_cast之一…...
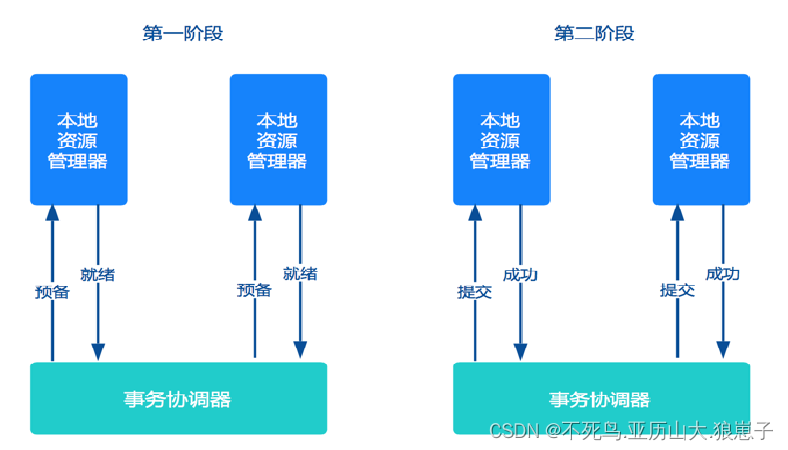
分布式事务(4):两阶段提交协议与三阶段提交区别
1 两阶段提交协议 两阶段提交方案应用非常广泛,几乎所有商业OLTP数据库都支持XA协议。但是两阶段提交方案锁定资源时间长,对性能影响很大,基本不适合解决微服务事务问题。 缺点: 如果协调者宕机,参与者没有协调者指…...
------ 实现多节点渲染【修改beginWork和completeWork】)
React源码解析18(9)------ 实现多节点渲染【修改beginWork和completeWork】
摘要 目前,我们已经实现了单节点的,beginWork,completeWork,diff流程。但是对于多节点的情况,比如: <div><span></span><span></span> </div>这种情况,我们还没有处…...

【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
