当前位置： 首页 > news >正文

[Android Framework] 系统 ANR 问题排查实践小结

news 2025/10/31 7:08:26

文章目录

  • 背景
  • 卡顿的定义：
  • 卡顿分类：
  • 卡顿原因汇总
  • ANR 出现的原理
  • 应用层导致ANR
  • 系统导致ANR
  • 日志抓取
    • traces.txt 是如何生成的
  • 分析思路与验证
  • 相关日志分析
    • data/anr/traces.txt
  • 其他分析思路
    • 如何分析生成的 trace.html 文件呢？
  • 最后解决
  • 参考：

背景

本文记录了工作中遇到的Andorid 系统层级 ANR 的问题排查及解决思路。

具体问题：在 VR一体机设备中遇到了第三方应用在视频播放时 当高标清切换时 出现了死机冻屏 的问题。

我们首先了解一下卡顿的

相关文章：

[Android Framework] 系统 ANR 问题排查实践小结

文章目录 背景卡顿的定义：卡顿分类：卡顿原因汇总ANR 出现的原理应用层导致ANR系统导致ANR日志抓取traces.txt 是如何生成的分析思路与验证相关日志分析data/anr/traces.txt其他分析思路如何分析生成的 trace.html 文件呢？最后解决参考：背景 本文记录了工作中遇到的Andorid …...

编程日记 2023/8/24 17:50:29

【Unity】Text文本组件的一些操作

Unity的Text组件的几种常见的操作方法 Text组件是Unity中用于在UI界面上显示文本的组件。它包含了一些常见的属性和方法，可以用来控制文本的内容、外观和交互。以下是一些常见的Text组件的操作： 设置文本内容：通过直接在Unity编辑器中的Text…...

编程日记 2023/8/24 17:49:28

如何通过tomcat下载映射下载文件

1.1找到tomcat服务器中server.xml文件 !--doBase是静态资源路径位置&#xff0c; path作用相当于设置的key, doBase作用相当于value --> <Context path"/download" docBase"E:\testBackData"></Context>1.2 找到tomcat服务器中web.xml文…...

编程日记 2023/8/24 17:48:27

Redis的8种数据结构和应用场景介绍，面试题答案

面试原题&#xff1a;你用过Redis哪些数据结构&#xff1f;&#xff08;网易一面 2023&#xff09;(面试题来自牛客网) 参考答案 后面有 详细答案解析&#xff0c;帮助更快记忆~ 参考答案共652字符&#xff0c;阅读约需1分8秒&#xff1b;全文共8694字符&#xff0c;阅读约需…...

编程日记 2023/8/24 17:47:26

Log4Qt日志框架（1）- 引入到QT中

Log4Qt日志框架&#xff08;1&#xff09;- 引入到QT中 1 下载源码2 简介3 加入到自己的项目中3.1 使用库文件3.2 引入源文件 4 说明 1 下载源码 github&#xff1a;https://github.com/MEONMedical/Log4Qt 官方(版本较老)&#xff1a;https://sourceforge.net/projects/log4q…...

编程日记 2023/8/24 17:46:24

【算法刷题之哈希表篇（1）】

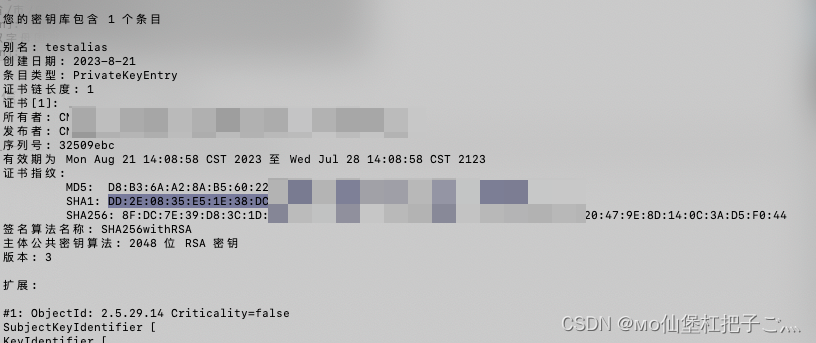
目录 1.哈希表基础理论2.leetcode-242. 有效的字母异位词&#xff08;1&#xff09;方法一&#xff1a;排序&#xff08;2&#xff09;方法二&#xff1a;哈希表 3.leetcode-349. 两个数组的交集&#xff08;1&#xff09;方法一&#xff1a;哈希表&#xff08;2&#xff09;方…...

编程日记 2023/8/24 17:45:22

uni-app 打包生成签名Sha1

Android平台打包发布apk应用&#xff0c;需要使用数字证书&#xff08;.keystore文件&#xff09;进行签名&#xff0c;用于表明开发者身份。 可以使用JRE环境中的keytool命令生成。以下是windows平台生成证书的方法&#xff1a; 安装JRE环境&#xff08;推荐使用JRE8环境&am…...

编程日记 2023/8/24 17:44:20

【Django】Django创建一个文件下载服务

当使用Django创建一个下载服务时&#xff0c;您可以设置一个视图来处理文件下载请求&#xff0c;并根据您的需求提供文件下载链接。以下是一个简单的示例&#xff0c;演示如何在Django中实现基本的文件下载服务&#xff1a; 创建Django项目和应用&#xff1a; 首先&#xff0c…...

编程日记 2023/8/24 17:43:19

Navicat for Mysql 显示 emoji 表情符号乱码问题 — 其它乱码情况都可参考

系统环境&#xff1a; 操作系统&#xff1a;MAC OS 10.11.6 MySQL&#xff1a;Server version: 5.6.21 MySQL Community Server (GPL) Navicat for MySQL: version 9.3.1 - standard 1、问题发现 在客户端执行用户注册&#xff0c;用户名包括 emoji 表情符号&#xff0c;注册完…...

编程日记 2023/8/24 17:42:17

《数字图像处理-OpenCV/Python》连载（2）目录

《数字图像处理-OpenCV/Python》连载&#xff08;2&#xff09;目录 本书京东优惠购书链接&#xff1a;https://item.jd.com/14098452.html 本书CSDN独家连载专栏&#xff1a;https://blog.csdn.net/youcans/category_12418787.html 第一部分 OpenCV-Python的基本操作 第1章 …...

编程日记 2023/8/24 17:41:15

Go学习-Day4

文章目录 Go学习-Day4函数值传递&#xff0c;引用传递常用的函数 异常处理数组Slice切片 Go学习-Day4 个人博客&#xff1a;CSDN博客 函数 值传递&#xff0c;引用传递 值传递直接拷贝值&#xff0c;一般是基本数据类型&#xff0c;数组&#xff0c;结构体也是引用传递传递…...

编程日记 2023/8/24 17:40:14

将el-dialog封装成函数调用

1、 使用Vue实例化方法 // MyDialog.js import Vue from vue export const openFormDialog function ({ props {}, events {} }) {const vm new Vue({data () {return {form: {}}},render () {return (<el-dialogvisible{true}{...{ props }}{...{ on: events }}onClos…...

编程日记 2023/8/24 17:39:12

Windows10批处理命令行设置环境变量笔记，无需重新安装python与chrome

近期&#xff0c;工作中经常安装、部署python生产、开发环境&#xff0c;比较麻烦&#xff0c;也没有心情去优化。突然&#xff0c;我的电脑崩溃了&#xff0c;在重新安装电脑的过程中&#xff0c;保留了原来的安装软件&#xff08;有的没有放在系统盘中&#xff09;&#xff0…...

编程日记 2023/8/24 17:38:11

统计学补充概念07-比较树

概念 在层次聚类中&#xff0c;聚类结果可以以树状结构表示&#xff0c;通常称为树状图&#xff08;Dendrogram&#xff09;。树状图展示了数据点如何被合并或分裂以形成聚类的层次结构。通过观察树状图&#xff0c;可以更直观地理解数据点之间的相似性和关系。 在比较树状图…...

编程日记 2023/8/24 17:37:10

设计原则 --《设计模式之美》总结篇

本文是阅读《设计模式之美》的总结和心得&#xff0c;跳过了书中对面试和工作用处不大或不多的知识点&#xff0c;总结总共分为三章&#xff0c;分别是面对对象编程范式、设计原则和设计模式。 设计模式是代码设计时的一些经验总结。相比于设计模式&#xff0c;设计原则更抽象。…...

编程日记 2023/8/24 17:36:08

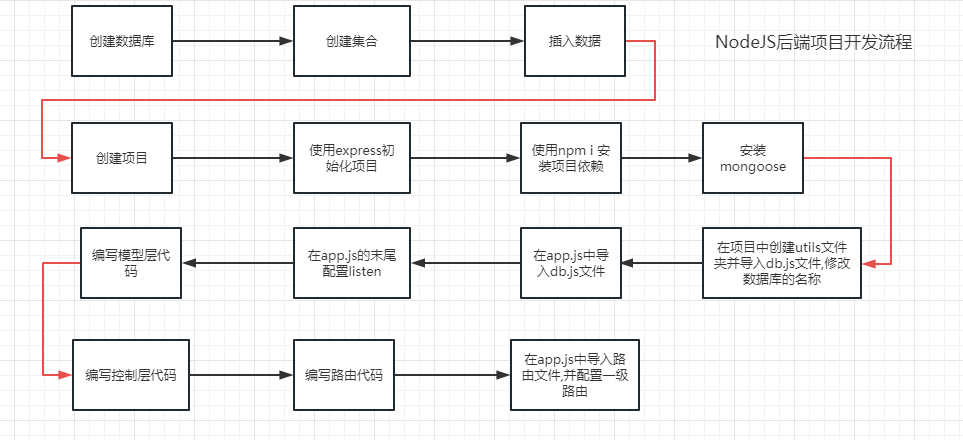
Day16-蜗牛影城后端开发

蜗牛影城后端开发 一 多表关联查询 电影集合movie的type(类别)字段关联到电影类别movieType表的_id(主键) 二 蜗牛影城后端开发 1 数据的导入导出 2 用户模块 UserModel.js //导入mongoose,并解构出Schema(类)和model(对象) const {Schema,model} =...

编程日记 2023/8/24 17:35:06

axios / fetch 实现 stream 流式请求

axios 是一个支持node端和浏览器端的易用、简洁且高效的http库。本文主要介绍 axios 如何实现 stream 流式请求&#xff0c;注意这里需要区分 node 环境和浏览器环境。 一、node端 代码演示&#xff1a; const axios require(axios);axios({method: get,url: http://tiven.c…...

编程日记 2023/8/24 17:34:04

Pytorch学习：torchvison.transforms常用包（ToTensor、Resize、Compose和RandomCrop）

torchvision.transforms常用包 1. torchvision.transforms.ToTensor2. torchvision.transforms.Resize3. torchvision.transforms.Compose4. torchvision.transforms.Normalize5. torchvision.transforms.RandomCrop 1. torchvision.transforms.ToTensor 将PIL Image或ndarray…...

编程日记 2023/8/24 17:33:03

算法通关村十二关 | 字符串转换

1. 转换小写字母 LeetCode709&#xff1a;给你一个字符串s&#xff0c;将该字符串中的大写字母转换成相同的小写字母&#xff0c;返回新的字符串。 每个字母都是有确定的ASCII的&#xff0c;可以根据码表操作子字符串&#xff0c;常见的ASCII范围是&#xff1a; a-z: 97-122, …...

编程日记 2023/8/24 17:32:02

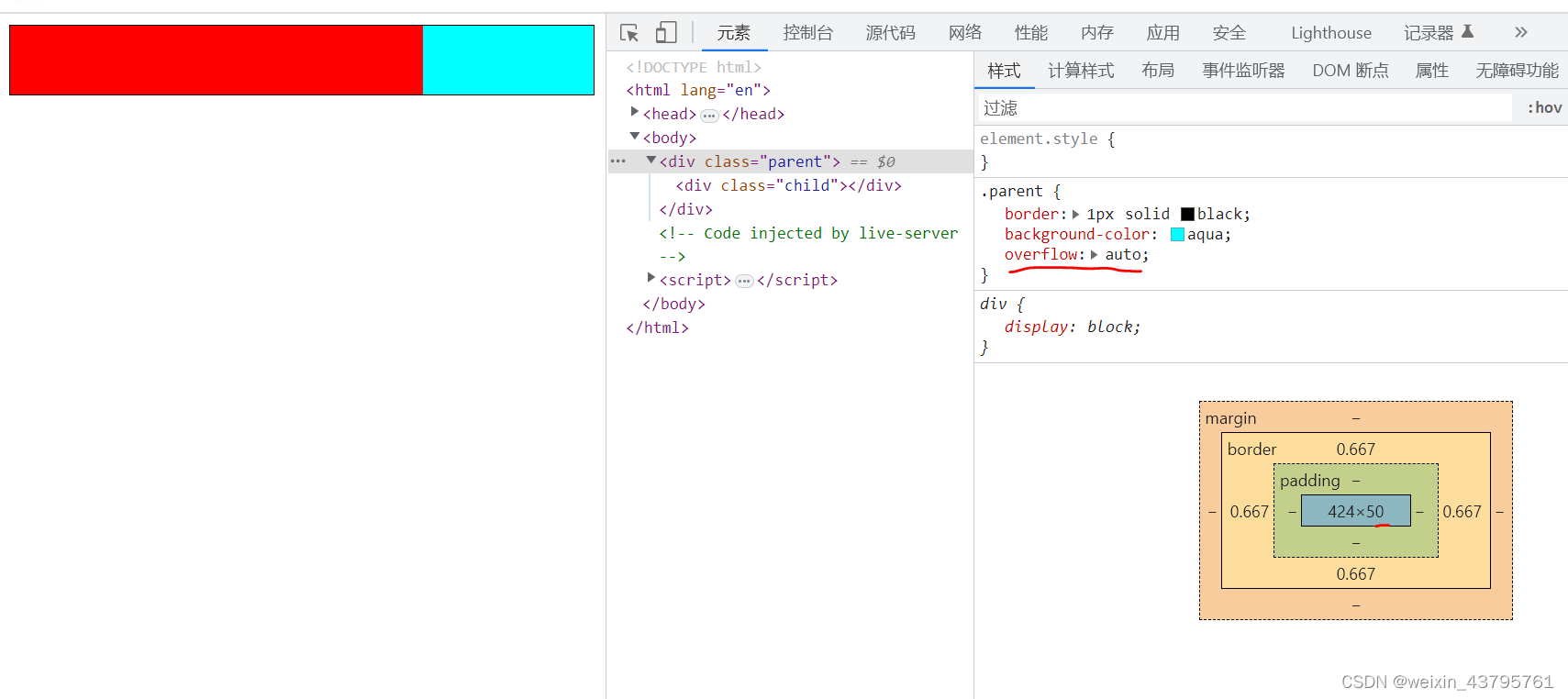
前端进阶Html+css09----BFC模型

1.什么是BFC模型 全称是&#xff1a;Block formatting context&#xff08;块级格式化上下文&#xff09;&#xff0c;是一个独立的布局环境&#xff0c;不受外界的影响。 2.FC,BFC,IFC 元素在标准流里都属于一个FC&#xff08;Formatting Context&#xff09;。 块级元素的布…...

编程日记 2023/8/24 17:31:00

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向&#xff1a; 逆向设计 通过神经网络快速预测微纳结构的光学响应&#xff0c;替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

编程新知 2025/10/30 10:46:13

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略&#xff0c;并且实现了基本的选区操作&#xff0c;还调研了自绘选区的实现。那么相对的&#xff0c;我们还需要设计编辑器的选区表达&#xff0c;也可以称为模型选区。编辑器中应用变更时的操作范围&#xff0c;就是以模型选区为基准来…...

编程新知 2025/9/5 17:56:03

FFmpeg 低延迟同屏方案

引言 在实时互动需求激增的当下&#xff0c;无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作&#xff0c;还是游戏直播的画面实时传输&#xff0c;低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架&#xff0c;凭借其灵活的编解码、数据…...

编程新知 2025/9/28 21:29:01

mongodb源码分析session执行handleRequest命令find过程

mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程&#xff0c;并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令&#xff0c;把数据流转换成Message&#xff0c;状态转变流程是&#xff1a;State::Created 》 St…...

编程新知 2025/8/16 7:00:37

CMake基础：构建流程详解

目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

编程新知 2025/10/28 0:22:33

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/8/9 13:14:15

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

编程新知 2025/7/4 0:50:01

算法：模拟

1.替换所有的问号 1576. 替换所有的问号 - 力扣&#xff08;LeetCode&#xff09; ​遍历字符串​&#xff1a;通过外层循环逐一检查每个字符。​遇到 ? 时处理​&#xff1a; 内层循环遍历小写字母&#xff08;a 到 z&#xff09;。对每个字母检查是否满足&#xff1a; ​与…...

编程新知 2025/10/26 21:21:16

【Go语言基础【12】】指针：声明、取地址、解引用

文章目录 零、概述&#xff1a;指针 vs. 引用&#xff08;类比其他语言&#xff09;一、指针基础概念二、指针声明与初始化三、指针操作符1. &&#xff1a;取地址&#xff08;拿到内存地址&#xff09;2. *&#xff1a;解引用&#xff08;拿到值&#xff09; 四、空指针&am…...

编程新知 2025/6/21 2:18:57

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变（硬件篇）

本项目是基于 STM32F103C8T6 微控制器的 SPWM（正弦脉宽调制）电源模块，能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路，图中 D1 为二极管， 其目的是防止正负极电源反接， …...

编程新知 2025/10/27 20:14:08