LA@向量组线性相关性
文章目录
- 向量组线性相关性
- 线性相关
- 线性无关
- 多向量向量组线性相关
- 单向量向量组的线性相关性
- 单位向量向量组线性相关性
- 双向量向量组的线性相关性
- 双向量线性相关的几何意义
- 三向量线性相关的几何意义
- 包含零向量的向量组线性相关
- 概念迁移:线性方程组和线性相关
- 齐次线性方程组和向量组线性相关性
- 向量组线性相关判定定理👺
- 概念补充
- 部分组
- 推论
- 方阵的行列式判定线性相关性
- 行数和列数的关系判定线性相关性
- 部分组线性相关的讨论
- 线性无关向量组添加一个向量后变为线性相关
- 证明1:
- 证明2:
- 先证明可表出
- 再证明 β \beta β的表示法唯一性
- 向量组线性相关性的简单判定🎈
- 例
- 例
- 例
- 综合例
- 证法1
- 证法2
- 证法3
- 小结
向量组线性相关性
- 线性相关性是向量组的一个重要属性
线性相关
-
给定向量组 A : α 1 , α 2 , ⋯ , α m A:\alpha_1,\alpha_2,\cdots,\alpha_m A:α1,α2,⋯,αm,若存在 m m m个 不全为 0 不全为0 不全为0的数 k 1 , k 2 , ⋯ , k m k_1,k_2,\cdots,k_m k1,k2,⋯,km,使得: ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}{k_i\alpha_i}=\bold{0} i=1∑mkiαi=0则称向量组 A A A线性相关
- ( α 1 , α 2 , ⋯ , α m ) ( k 1 k 2 ⋮ k m ) = ∑ i = 1 m k i α i = 0 (\alpha_1,\alpha_2,\cdots,\alpha_m) \begin{pmatrix} k_{1} \\ k_{2} \\ \vdots \\ k_{m} \\ \end{pmatrix} =\sum\limits_{i=1}^{m}{k_i\alpha_i}=\bold{0} (α1,α2,⋯,αm) k1k2⋮km =i=1∑mkiαi=0
线性无关
-
如果向量组不是线性相关的,则是线性无关的
-
向量组 A A A线性无关还可以描述为:
- 使得 ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}{k_i\alpha_i}=\bold0 i=1∑mkiαi=0成立的s个数 k 1 , k 2 , ⋯ , k s k_1,k_2,\cdots,k_s k1,k2,⋯,ks全为0
多向量向量组线性相关
-
对于 A : α 1 , ⋯ , α m A:\alpha_1,\cdots,\alpha_m A:α1,⋯,αm, m ⩾ 2 m\geqslant{2} m⩾2时, A A A线性相关等价于 A A A中至少有一个向量能由其余 m − 1 m-1 m−1个向量线性表示
-
证明:
- 若 A A A线性相关,存在 m m m个 不全为 0 不全为0 不全为0的数 k 1 , k 2 , ⋯ , k m k_1,k_2,\cdots,k_m k1,k2,⋯,km,使得: ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}{k_i\alpha_i}=\bold{0} i=1∑mkiαi=0,不妨设 k 1 ≠ 0 k_1\neq{0} k1=0(若 k i ≠ 0 k_i\neq{0} ki=0,可以通过调整 k i , α i k_i,\alpha_i ki,αi顺序到 k 1 ( α 1 ) k_1(\alpha_1) k1(α1),使得 k 1 ≠ 0 k_1\neq{0} k1=0,这不改变线性相关性)
- 对 ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}{k_i\alpha_i}=\bold{0} i=1∑mkiαi=0两边同时除以 k 1 k_1 k1, ∑ i = 1 m k i k 1 α i {\sum\limits_{i=1}^{m}{\frac{k_i}{k_1}\alpha_i}} i=1∑mk1kiαi= α 1 + ∑ i = 2 m k i k 1 α i \alpha_1+\sum_{i=2}^{m}\frac{k_i}{k_1}\alpha_i α1+∑i=2mk1kiαi= 0 \bold{0} 0;即 α 1 = ∑ i = 2 m k i k 1 α i \alpha_1=\sum_{i=2}^{m}\frac{k_i}{k_1}\alpha_i α1=∑i=2mk1kiαi
- 反之,若 α 1 = ∑ i = 2 m k i α i \alpha_1=\sum_{i=2}^{m}k_i\alpha_i α1=∑i=2mkiαi; − α 1 + ∑ i = 2 m k i α i = 0 -\alpha_1+\sum_{i=2}^{m}k_i\alpha_i=\bold{0} −α1+∑i=2mkiαi=0,即至少存在 − 1 , k 2 , ⋯ , k m -1,k_2,\cdots,k_m −1,k2,⋯,km这 m m m个不全为0的数使得 ∑ i = 1 m k i α i = 0 \sum_{i=1}^{m}k_i\alpha_i=\bold{0} ∑i=1mkiαi=0,即 A A A线性相关
-
其逆否命题也是成立的:若 A : α 1 , ⋯ , α m A:\alpha_1,\cdots,\alpha_m A:α1,⋯,αm中任意一个向量都不能被其他 m − 1 m-1 m−1线性表示,则 A A A线性无关
单向量向量组的线性相关性
- 对于单个向量构成的向量组 A : α 1 A:\alpha_1 A:α1,若要满足A线性相关,即存在 k ≠ 0 k\ne{0} k=0使得 k α 1 = 0 k\alpha_1=0 kα1=0,只有当 α 1 = 0 \alpha_1=\bold{0} α1=0成立
- 可见单个非零向量构成的向量组线性无关
单位向量向量组线性相关性
- 设 E n = ( ϵ 1 , ⋯ , ϵ n ) \bold{E}_n=(\epsilon_1,\cdots,\epsilon_n) En=(ϵ1,⋯,ϵn)
- 由 n n n个 n n n维单位向量 E n : ϵ 1 , ⋯ , ϵ n E_n:\epsilon_1,\cdots,\epsilon_n En:ϵ1,⋯,ϵn构成的向量组线性无关
- 证明: ∑ i = 1 n k i ϵ i = ( k 1 , k 2 , ⋯ , k s ) \sum\limits_{i=1}^{n}k_{i}\epsilon_{i}=(k_1,k_2,\cdots,k_s) i=1∑nkiϵi=(k1,k2,⋯,ks)= 0 \bold{0} 0的解只有 k 1 = k 2 = ⋯ = k s = 0 k_1=k_2=\cdots=k_s=0 k1=k2=⋯=ks=0
双向量向量组的线性相关性
- 设 A : α 1 , α 2 A:\alpha_1,\alpha_2 A:α1,α2,则 A A A线性相关的充要条件是 α 1 , α 2 \alpha_1,\alpha_2 α1,α2分量对应成比例,即 α 1 = k α 2 \alpha_1=k\alpha_2 α1=kα2
- 证法1:
- 充分性: α 1 = k α 2 \alpha_1=k\alpha_2 α1=kα2即 α 1 − k α 2 = 0 \alpha_1-k\alpha_2=\bold{0} α1−kα2=0,所以存在不全为0的 ( k 1 , k 2 ) = ( 1 , k ) (k_1,k_2)=(1,k) (k1,k2)=(1,k)满足 k 1 α 1 + k 2 α 2 = 0 k_1\alpha_1+k_2\alpha_2=\bold{0} k1α1+k2α2=0
- 必性: A A A线性相关则存在不全为0的 k 1 , k 2 k_1,k_2 k1,k2(不妨假设 k 1 ≠ 0 k_1\neq{0} k1=0)使得 k 1 α 1 + k 2 α 2 = 0 k_1\alpha_1+k_2\alpha_2=\bold{0} k1α1+k2α2=0,即 α 1 = − k 2 k 1 α 2 \alpha_1=-\frac{k_2}{k_1}\alpha_2 α1=−k1k2α2,取 k = − k 2 k 1 k=-\frac{k_2}{k_1} k=−k1k2
- 证法2:
- α 1 = k α 2 \alpha_1=k\alpha_2 α1=kα2说明 A A A中存在一个向量 α 1 \alpha_1 α1能被其余向量 ( α 2 ) (\alpha_2) (α2)线性表示,所以 A A A线性相关
双向量线性相关的几何意义
- 两个向量线性相关的几何意义是两向量共线(对于高维向量仍沿用共线几何术语)
三向量线性相关的几何意义
- 三向量线性相关的几何意义是三向量共面(对于高维向量,是超平面共面,仍然沿用几何术语)
包含零向量的向量组线性相关
-
任意一个包含零向量的向量组总是线性相关的
- 假设向量组 A : α 1 , α 2 , ⋯ , α m A:\alpha_1,\alpha_2,\cdots,\alpha_m A:α1,α2,⋯,αm,中 α 1 = 0 \alpha_1=\bold{0} α1=0(如果不是,则将 α 1 \alpha_1 α1调整为非零向量),则令 k i = 0 , ( i = 2 , ⋯ , m ) k_i=0,(i=2,\cdots,m) ki=0,(i=2,⋯,m)则: α 1 \alpha_1 α1= ∑ i = 2 m k i α i = 0 \sum\limits_{i=2}^{m}k_i\alpha_i=\bold{0} i=2∑mkiαi=0所以 A A A线性相关
概念迁移:线性方程组和线性相关
- 向量组的线性相关和线性无关的概念可以迁移到线性方程组
- 当方程组 A x = b \bold{Ax=b} Ax=b中某个方程 r s r_s rs是其余方程的线性组合时,这个方程 r s r_s rs是多余的(可移除的,不影响方程组的解的)
- 这种情况下,方程组是线性相关的(指方程组内各个方程式线性相关的)
- 若方程组中没有多余方程(任何方程都无法被方程组内其余方程线性表示),就称方程组线性无关(线性独立)
- 可见,方程组 A x = b \bold{Ax=b} Ax=b线性相关的充要条件是矩阵 B = ( A , b ) \bold{B=(A,b)} B=(A,b)的行向量组线性相关
- 设向量组 A : a 1 , a 2 , ⋯ , a m A:\bold{a}_1,\bold{a}_2,\cdots,\bold{a}_m A:a1,a2,⋯,am构成的矩阵为 A = ( a 1 , a 2 , ⋯ , a m ) \bold{A}=(\bold{a}_1,\bold{a}_2,\cdots,\bold{a}_m) A=(a1,a2,⋯,am),向量组 A A A线性相关等价于: ∑ i = 1 m x i a i = 0 \sum_{i=1}^{m}x_i\bold{a}_i=\bold{0} ∑i=1mxiai=0,即齐次线性方程组 A x = 0 \bold{Ax=0} Ax=0有非零解(存在自由未知数)
- 由此,我们将向量组线性相关转换为矩阵问题(线性方程组的解的问题)
齐次线性方程组和向量组线性相关性
- m m m个 n n n维向量构成的向量组 A : α 1 , α 2 , ⋯ , α m A:\alpha_1,\alpha_2,\cdots,\alpha_m A:α1,α2,⋯,αm,则线性相关的充要条件是:线性方程组 A x = 0 \bold{Ax}=\bold0 Ax=0有非零解
- 其中 A A A构成的矩阵 A \bold{A} A是 n × m n\times{m} n×m,
- 若 r ( A ) = m r(A)=m r(A)=m,方程组有唯一解零解, A A A线性无关
- 若 r ( A ) < m r(A)<m r(A)<m,方程有多解(非零解), A A A线性相关
向量组线性相关判定定理👺
- 将上一节归纳为定理:
- 包含 m m m个向量的向量组 A A A线性相关的充要条件是 R ( A ) < m R(\bold{A})<m R(A)<m; A A A线性无关的充要条件是 R ( A ) = m R(\bold{A})=m R(A)=m
- 简称:小相关,等无关
- 该定理相当重要,很多场景下可以比线性相关定义更加方便的推导和证明一些线性相关的命题和结论
概念补充
部分组
-
若向量组 A A A是向量组 B B B的一部分,则 A A A是 B B B的部分组,相对的可以称 B B B为全组
-
例如 A : α 1 , ⋯ , α m A:\alpha_1,\cdots,\alpha_m A:α1,⋯,αm是向量组 B : α 1 , ⋯ , α m , α m + 1 B:\alpha_1,\cdots,\alpha_m,\alpha_{m+1} B:α1,⋯,αm,αm+1的部分组
推论
方阵的行列式判定线性相关性
- 特别的,若 A A A是一个 m m m阶方阵,则 A A A线性线相关的条件 R ( A ) = m R(\bold{A})=m R(A)=m还可以作 ∣ A ∣ ≠ 0 |\bold{A}|\neq{0} ∣A∣=0
行数和列数的关系判定线性相关性
- A n × m \bold{A}_{n\times{m}} An×m当行数 n < m n<m n<m时, R ( A ) ⩽ n < m R(\bold{A})\leqslant{n}<m R(A)⩽n<m此时 A A A必定线性相关
- 这个结论指出,如果向量组行数少或列数多的情况下,无论各个向量内容如何,向量组一定是线性相关的.特别是向量组包含无穷多个向量时
- 同时说明了,对于 n n n维向量构成的向量组 A A A,只要向量数量够多, A A A一定是线性相关
部分组线性相关的讨论
-
如果向量组 A : α 1 , ⋯ , α m A:\alpha_1,\cdots,\alpha_m A:α1,⋯,αm线性相关,则向量组 B : α 1 , ⋯ , α m , α m + 1 B:\alpha_1,\cdots,\alpha_m,\alpha_{m+1} B:α1,⋯,αm,αm+1 的也线性相关;
- 反之(逆否命题,可以用反证法),若 B B B线性无关,则 A A A也线性无关
- 由于成比例的两个向量线性相关,从而若某个向量组包含一对成比例的向量(部分向量组线性相关),则这个向量组是线性相关的
-
证明:
-
由于 A A A线性相关,所以 R ( A ) < m R(\bold{A})<m R(A)<m
-
由 A , B A,B A,B可知, B = ( A , α m + 1 ) \bold{B=(A,\alpha_{m+1})} B=(A,αm+1), R ( B ) ⩽ R ( A ) + R ( α m + 1 ) ⩽ R ( A ) + 1 R(\bold{B})\leqslant{R(\bold{A})+R(\alpha_{m+1})}\leqslant R(\bold{A})+1 R(B)⩽R(A)+R(αm+1)⩽R(A)+1< m + 1 m+1 m+1;
-
所以 B B B线性相关
-
-
推广:若 B B B是 A A A增加多个向量,则依然成立;即
-
部分组线性相关,则全组线性相关;
-
若全组线性无关,则部分组线性无关
-
线性无关向量组添加一个向量后变为线性相关
- 若向量组 A : α 1 , α 2 , ⋯ , α s A:\alpha_1,\alpha_2,\cdots,\alpha_s A:α1,α2,⋯,αs线性无关,而向量组 B : α 1 , α 2 , ⋯ , α s , β B:\alpha_1,\alpha_2,\cdots,\alpha_s,\beta B:α1,α2,⋯,αs,β线性相关,则 β \beta β可以由向量 A A A线性表示,且表示法唯一.
证明1:
- 记 A = ( α 1 , ⋯ , α m ) \bold{A}=(\alpha_1,\cdots,\alpha_m) A=(α1,⋯,αm), B = ( α 1 , ⋯ , a m , β ) \bold{B}=(\alpha_1,\cdots,a_m,\beta) B=(α1,⋯,am,β),有 R ( A ) ⩽ R ( B ) R(\bold{A})\leqslant{R(\bold{B})} R(A)⩽R(B)
- 因为 A A A线性无关,所以 R ( A ) = m R(\bold{A})=m R(A)=m;又因为 B B B线性相关,所以 R ( B ) < m + 1 R(\bold{B})<m+1 R(B)<m+1
- 所以 m ⩽ R ( B ) < m + 1 m\leqslant{R(\bold{B})}<m+1 m⩽R(B)<m+1,即 R ( B ) = m R(\bold{B})=m R(B)=m,
- 对于方程组 A x = β \bold{Ax=\beta} Ax=β有 R ( A ) = R ( A , β ) = R ( B ) = m R(\bold{A})=R(\bold{A,\beta})=R(\bold{B})=m R(A)=R(A,β)=R(B)=m,可见 A x = β \bold{Ax=\beta} Ax=β有唯一解,即 B B B可以被 A A A唯一的线性表示
证明2:
先证明可表出
-
由于 B B B线性相关,则存在不全为0的 k 1 , ⋯ , k m , k m + 1 k_1,\cdots,k_m,k_{m+1} k1,⋯,km,km+1,使得 ( ∑ i = 1 m k i α i ) + k m + 1 β = 0 (\sum\limits_{i=1}^{m}k_i\alpha_i)+k_{m+1}\beta=0 (i=1∑mkiαi)+km+1β=0
-
case1:若 k m + 1 = 0 k_{m+1}=0 km+1=0则 ( ∑ i = 1 m k i α i ) + k m + 1 β = 0 (\sum\limits_{i=1}^{m}k_i\alpha_i)+k_{m+1}\beta=0 (i=1∑mkiαi)+km+1β=0可以推出 ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}k_i\alpha_i=0 i=1∑mkiαi=0
- 而由 A A A线性无关知,只有 k 1 , ⋯ , k m = 0 k_1,\cdots,k_m=0 k1,⋯,km=0时,有 ∑ i = 1 m k i α i = 0 \sum\limits_{i=1}^{m}k_i\alpha_i=0 i=1∑mkiαi=0成立
- 从而 k 1 , ⋯ , k m , k m + 1 = 0 k_1,\cdots,k_m,k_{m+1}=0 k1,⋯,km,km+1=0, B B B线性无关,和条件矛盾,从而 k m + 1 ≠ 0 k_{m+1}\ne{0} km+1=0
-
case2: k m + 1 ≠ 0 k_{m+1}\neq{0} km+1=0, β = − 1 k m + 1 ∑ i = 1 m k i α i \beta=-\frac{1}{k_{m+1}}\sum\limits_{i=1}^{m}k_i\alpha_i β=−km+11i=1∑mkiαi
再证明 β \beta β的表示法唯一性
-
利用反证法
-
设 β \beta β可以被表示为 β = ∑ i = 1 m k i α i = ∑ i = 1 m l i α i \beta=\sum\limits_{i=1}^{m}k_i\alpha_i=\sum\limits_{i=1}^{m}l_i\alpha_i β=i=1∑mkiαi=i=1∑mliαi
-
对两种表示方法做差: ∑ i = 1 m ( k i − l i ) α i = 0 \sum\limits_{i=1}^{m}(k_i-l_i)\alpha_i=\bold0 i=1∑m(ki−li)αi=0
-
而由 A A A线性无关知,只有 k i − l i = 0 ( i = 1 , 2 , ⋯ , s ) k_i-l_i=0(i=1,2,\cdots,s) ki−li=0(i=1,2,⋯,s)时才有 ∑ i = 1 m ( k i − l i ) α i = 0 \sum\limits_{i=1}^{m}(k_i-l_i)\alpha_i=\bold0 i=1∑m(ki−li)αi=0成立
-
从而 k i = l i ( i = 1 , 2 ⋯ , n ) k_i=l_i(i=1,2\cdots,n) ki=li(i=1,2⋯,n)
-
所以表示法唯一
向量组线性相关性的简单判定🎈
- 包含以下向量(一种或多种)的向量组线性相关
- 零向量
- 相等向量对
- 成比例的向量对
例
- n n n维单位坐标向量组 E : e 1 , ⋯ , e n E:\bold{e}_1,\cdots,\bold{e}_n E:e1,⋯,en的线性相关性:
- 设 E E E构成的矩阵 E = ( e 1 , ⋯ , e n ) \bold{E}=(\bold{e}_1,\cdots,\bold{e}_n) E=(e1,⋯,en), R ( E ) R(\bold{E}) R(E)= n n n,所以 E E E线性无关
例
-
矩阵A的列向量组:
-
α 1 = ( 3 , − 1 , 3 , 1 ) T \alpha_1=(3,-1,3,1)^T α1=(3,−1,3,1)T
-
α 2 = ( 4 , − 2 , 5 , 4 ) T \alpha_2=(4,-2,5,4)^T α2=(4,−2,5,4)T
-
α 3 = ( 2 , − 1 , 4 , − 1 ) T \alpha_3=(2,-1,4,-1)^T α3=(2,−1,4,−1)T
-
-
求证 A A A线性相关,并求 A A A的列向量组的一个线性相关关系
-
A = ( α 1 , α 2 , α 3 ) = ( 2 4 2 − 1 − 2 − 1 3 5 4 1 4 − 1 ) A ∼ r A ~ = ( 1 0 3 0 1 − 1 0 0 0 0 0 0 ) \bold{A}=(\alpha_1,\alpha_2,\alpha_3) =\begin{pmatrix} 2& 4& 2 \\ -1& -2& -1 \\ 3& 5& 4 \\ 1& 4& -1 \\ \end{pmatrix} \\ A\overset{r}{\sim} \widetilde{A}=\begin{pmatrix} 1& 0& 3 \\ 0& 1& -1 \\ 0& 0& 0 \\ 0& 0& 0 \\ \end{pmatrix} A=(α1,α2,α3)= 2−1314−2542−14−1 A∼rA = 100001003−100
-
由于 r ( A ) = r ( A ~ ) = 2 < n = 3 r(A)=r(\widetilde{A})=2<n=3 r(A)=r(A )=2<n=3,所以 A A A线性相关,存在 n − r = 3 − 2 = 1 n-r=3-2=1 n−r=3−2=1个自由变量,不妨令 ( x 3 ) (x_3) (x3)为自由变量
-
容易读出 x 1 + 3 x 3 = 0 , x 2 − x 3 = 0 x_1+3x_3=0,x_2-x_3=0 x1+3x3=0,x2−x3=0
-
x 1 = − 3 x 3 x_1=-3x_3 x1=−3x3;
-
x 2 = x 3 x_2=x_3 x2=x3
-
-
取 x 3 = − 1 x_3=-1 x3=−1,则得到一个特解 ( x 1 , x 2 , x 3 ) T = ( 3 , − 1 , − 1 ) T (x_1,x_2,x_3)^T=(3,-1,-1)^T (x1,x2,x3)T=(3,−1,−1)T
-
此时有 3 α 1 − α 2 − α 3 = 0 3\alpha_1-\alpha_2-\alpha_3=\bold{0} 3α1−α2−α3=0成立
-
例
设某一个范德蒙行列式
-
∣ V ∣ = ∣ 1 1 1 ⋯ 1 a 1 a 2 a 3 ⋯ a n a 1 2 a 2 2 a 3 2 ⋯ a n 2 ⋮ ⋮ ⋮ ⋮ a 1 n − 1 a 2 n − 1 a 3 n − 1 ⋯ a n n − 1 ∣ n 记 α j = ( 1 a i a i 2 ⋮ a i n − 1 ) j = 1 , 2 , ⋯ , n |V| =\begin{vmatrix} 1 &1 &1 &\cdots &1 \\ a_{1}&a_{2}&a_{3}&\cdots &a_{n} \\ a_{1}^{2}&a_{2}^{2}&a_{3}^{2}&\cdots &a_{n}^{2} \\ \vdots &\vdots &\vdots & &\vdots \\ a_{1}^{n-1}&a_{2}^{n-1}&a_{3}^{n-1}&\cdots &a_{n}^{n-1} \\ \end{vmatrix}_{n} \\ 记\alpha_j =\begin{pmatrix} 1 \\ a_{i} \\ a_{i}^{2} \\ \vdots \\ a_{i}^{n-1}\\ \end{pmatrix} j=1,2,\cdots,n ∣V∣= 1a1a12⋮a1n−11a2a22⋮a2n−11a3a32⋮a3n−1⋯⋯⋯⋯1anan2⋮ann−1 n记αj= 1aiai2⋮ain−1 j=1,2,⋯,n
-
∣ V ∣ = ∣ α 1 , α 2 , ⋯ , α n ∣ |V|=|\alpha_1,\alpha_2,\cdots,\alpha_n| ∣V∣=∣α1,α2,⋯,αn∣,若其中 a i , ( i = 1 , 2 , ⋯ , n ) a_i,(i=1,2,\cdots,n) ai,(i=1,2,⋯,n)互不相等.则 ∣ V ∣ ≠ 0 |V|\neq{0} ∣V∣=0,从而向量组 A : α 1 , α 2 , ⋯ , α n A:\alpha_1,\alpha_2,\cdots,\alpha_n A:α1,α2,⋯,αn线性无关
综合例
-
设
-
β 1 = α 1 + α 2 \beta_1=\alpha_1+\alpha_2 β1=α1+α2
-
β 2 = α 2 + α 3 \beta_2=\alpha_2+\alpha_3 β2=α2+α3
-
β 3 = α 3 + α 1 \beta_3=\alpha_3+\alpha_1 β3=α3+α1
-
-
求证若 A : α 1 , α 2 , α 3 A:\alpha_1,\alpha_2,\alpha_3 A:α1,α2,α3线性无关,则 B : β 1 , β 2 , β 3 B:\beta_1,\beta_2,\beta_3 B:β1,β2,β3线性无关
证法1
- 设向量 x = ( x 1 , x 2 , x 3 ) T \bold{x}=(x_1,x_2,x_3)^T x=(x1,x2,x3)T使得 ∑ i = 1 3 x i β i = 0 \sum_{i=1}^{3}x_i\beta_i=\bold{0} ∑i=13xiβi=0,即 x 1 ( α 1 + α 2 ) + x 2 ( α 2 + α 3 ) + x 3 ( α 3 + α 1 ) x_1(\alpha_1+\alpha_2)+x_2(\alpha_2+\alpha_3)+x_3(\alpha_3+\alpha_1) x1(α1+α2)+x2(α2+α3)+x3(α3+α1)= 0 \bold{0} 0
- 即 ( x 1 + x 3 ) α 1 + ( x 1 + x 2 ) α 2 + ( x 2 + x 3 ) α 3 = 0 (x_1+x_3)\alpha_1+(x_1+x_2)\alpha_2+(x_2+x_3)\alpha_3=\bold{0} (x1+x3)α1+(x1+x2)α2+(x2+x3)α3=0
- 由于 A A A线性无关,所以 ∑ i = 1 3 k i α i = 0 \sum_{i=1}^{3}k_i\alpha_i=0 ∑i=13kiαi=0只有当 k 1 = k 2 = k 3 = 0 k_1=k_2=k_3=0 k1=k2=k3=0
- x 1 + x 3 = 0 x_1+x_3=0 x1+x3=0
- x 1 + x 2 = 0 x_1+x_2=0 x1+x2=0
- x 2 + x 3 = 0 x_2+x_3=0 x2+x3=0
- 由初等变换法(或cramer法则),该方程组有唯一解零解
- 即 ∑ i = 1 3 x i β i = 0 \sum_{i=1}^{3}x_i\beta_i=\bold{0} ∑i=13xiβi=0只有零解,向量组 B B B线性无关
证法2
-
把条件中的向量等式体现的是向量组 B B B可以由向量组 A A A线性表出
-
用一个矩阵等式表达:
-
将 A , B A,B A,B的矩阵分别用列分块矩阵表示 B 1 × 3 \bold{B}_{1\times{3}} B1×3= ( β 1 , β 2 , β 3 ) (\beta_1,\beta_2,\beta_3) (β1,β2,β3), A 1 × 3 \bold{A}_{1\times{3}} A1×3= ( α 1 , α 2 , α 3 ) (\alpha_1,\alpha_2,\alpha_3) (α1,α2,α3)
-
表出系数矩阵设为 K 3 × 3 \bold{K}_{3\times{3}} K3×3,矩阵表达式为 B = A K \bold{B=AK} B=AK
-
再分别根据3个向量等式中 α i \alpha_i αi的系数 ( i = 1 , 2 , 3 ) (i=1,2,3) (i=1,2,3),填写 K K K的3个列
-
( β 1 , β 2 , β 3 ) = ( α 1 , α 2 , α 3 ) ( 1 1 1 1 1 0 0 1 1 ) (\beta_1,\beta_2,\beta_3) =(\alpha_1,\alpha_2,\alpha_3) \begin{pmatrix} 1&1&1\\ 1&1&0\\ 0&1&1 \end{pmatrix} (β1,β2,β3)=(α1,α2,α3) 110111101
-
设 B x = 0 \bold{Bx=0} Bx=0,将 B = A K \bold{B=AK} B=AK代入 B x = 0 \bold{Bx=0} Bx=0,再由乘法结合律,得 A ( K x ) = 0 \bold{A(Kx)=0} A(Kx)=0,这就将 B B B得线性相关性转化到 A A A得线性相关性上,利用 A A A的线性相关性判断 B B B的线性相关性
-
而 A A A是线性无关的,所以 A y = 0 \bold{Ay=0} Ay=0只有零解,即 y = K x = 0 \bold{y=Kx=0} y=Kx=0,
-
因为 ∣ K ∣ = 2 ≠ 0 |\bold K|=2\neq{0} ∣K∣=2=0,所以 K x = 0 \bold{Kx=0} Kx=0只有零解,即 x = 0 \bold{x=0} x=0,从而 B B B线性无关
-
证法3
- 和证法3类似,但是这里采用向量组的秩判断向量组的线性相关性
- 因为 K \bold{K} K可逆,则 R ( K ) = 3 R(\bold{K})=3 R(K)=3
- 由矩阵秩的性质,对于 B = A K \bold{B=AK} B=AK,有 R ( A K ) = R ( A ) R(\bold{AK})={R(\bold{A})} R(AK)=R(A),而 A A A线性无关,所以 R ( A ) = 3 R(\bold{A})=3 R(A)=3(向量组 A , B A,B A,B包含的向量个数都是3)
- 所以 R ( B ) = R ( A ) = 3 R(\bold{B})=R(\bold{A})=3 R(B)=R(A)=3所以向量组 B B B线性无关
小结
- 证法1是按线性相关的定义,通过向量的运算得到的以 K \bold{K} K为系数矩阵的齐次方程,再把问题转化为它只有令解进行推理
- 证法2,3都是先将三个向量等式合并为矩阵等式,立即得到矩阵 K \bold{K} K
- 证法2把证明向量组线性无关转化为证明齐次方程没有非零解,而去考察方程 B x = 0 \bold{Bx=0} Bx=0
- 证法3利用矩阵的秩的知识,以及向量组线性相关判定定理,避开了线性方程而直接证明
相关文章:

LA@向量组线性相关性
文章目录 向量组线性相关性线性相关线性无关多向量向量组线性相关单向量向量组的线性相关性单位向量向量组线性相关性双向量向量组的线性相关性双向量线性相关的几何意义三向量线性相关的几何意义包含零向量的向量组线性相关概念迁移:线性方程组和线性相关齐次线性方程组和向量…...

[k8s] 基于ubuntu22部署k8s1.28记录
k8s1.28部署已经不依赖docker了,所以不需要安装docker。同理:如果想查看镜像和运行容器,也不能用docker命令去查询了:需要使用crictl。不过crictl命令参数兼容docker,所以使用上手没有啥难度。 1. 配置安装源 根据k8…...

React 事件代理 和原生事件绑定混用:你的选择会导致什么问题?
在React开发中,事件处理是一个常见的任务。React提供了一个方便的事件系统,但有时我们可能会在React组件中与原生DOM事件一起使用。本文将讨论React的事件代理机制与原生事件绑定混用可能导致的一些问题。 React的事件代理 React采用了一种称为"事…...

使用阿里云国外和国内云服务器有什么注意事项?
使用阿里云的国外和国内云服务器时,有一些注意事项需要考虑: 地理位置:选择离你的用户或数据中心最近的地理位置,可以减少延迟和提高访问速度。对于国内用户,使用国内云服务器可能更好;对于国外用户&#…...
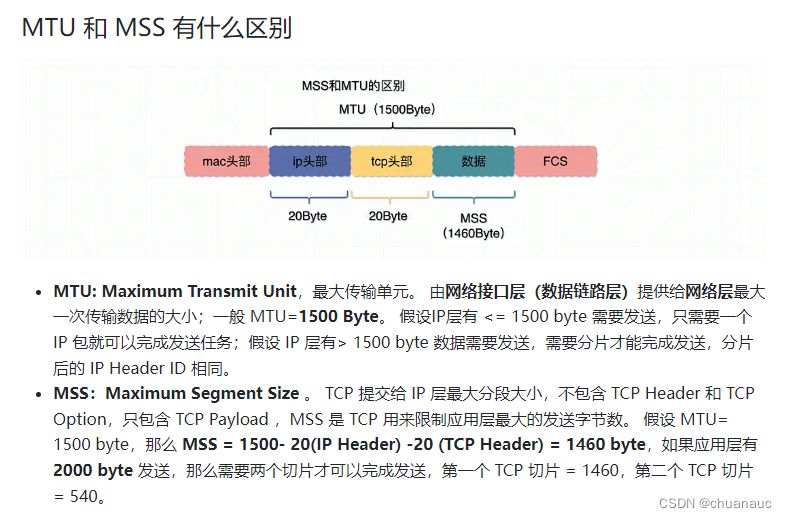
【计算机网络】【常考问题总结】
1. ping 127.0.0.1 后会发生什么? ping 127.0.0.1 ;ping 0.0.0.0 ; ping localhost 面试官问:断网了,还能ping通 127.0.0.1 吗?为什么?_kevin_tech的博客-CSDN博客 2. MTU,MMU是…...
前端基础(props emit slot 父子组件间通信)
前言:如何实现组件的灵活使用,今天学习组件封装用到的props、slot和emit。 目录 props 子组件 父组件 示例代码 slot 示例代码 作用域插槽 emit 示例代码 props 需要实现在其他组件中使用同一个子组件。 子组件 子组件(所谓子组件…...

即时通讯:短轮询、长轮询、SSE 和 WebSocket 间的区别
在现代 Web 开发中,即时通讯已经成为许多应用程序的重要组成部分。为了实现即时通讯,开发人员通常使用不同的技术和协议。本文将介绍四种常见的即时通讯实现方法:短轮询、长轮询、SSE(服务器发送事件)和 WebSocket&…...

高忆管理:药店零售概念回落,开开实业走低,此前7日大涨超80%
药店零售概念18日盘中大幅下挫,到发稿,华人健康跌逾11%,漱玉布衣、塞力医疗跌超9%,重药控股、浙江震元、榜首医药等跌超7%,药易购跌超6%,开开实业跌超3%。 值得注意的是,开开实业此前7个交易日斩…...

Go1.19 排序算法设计实践 经典排序算法对比
详解经典排序算法 01 为什么要学习数据结构与算法 抖音直播排行榜功能 案例 规则:某个时间段内,直播间礼物数TOP10房间获得奖励,需要在每个房间展示排行榜解决方案 •礼物数量存储在Redis-zset中,使用skiplist使得元素整体有序 •…...
3:Ubuntu上配置QT交叉编译环境并编译QT程序到Jetson Orin Nano(ARM)
1.Ubuntu Qt 配置交叉编译环境 1.1 ubuntu 20.04安装Qt sudo apt-get install qtcreator 1.2 配置QT GCC配置同上 最后配置Kits 上面设置完成之后 ,设置Kits 中的Device(这是为了能够直接把项目部署到arm设备上) 点击NEXT之后会出现连接被拒绝,不用担…...
CentOS下MySQL的彻底卸载的几种方法
这里我为大家详细讲解下“CentOS下MySQL的彻底卸载的几种方法”的完整攻略。 前言 先通过下列命令找到需要删除的相关文件 rpm -qa mysql* whereis mysql find / -name mysql 需要上传的命令介绍 删除 MySQL 数据目录 rm -rf /var/lib/mysql 删除配置文件 rm -rf /etc/my.cnf…...

Spring 的异常处理机制
Spring 的异常处理机制 在Spring中,异常处理是一个非常重要的方面,用于捕获和处理应用程序中可能出现的异常情况。Spring提供了多种方式来处理异常。 使用Spring的异常处理机制主要有以下优点: **统一的异常处理:**通…...

java八股文面试[JVM]——JVM参数
参考:JVM学习笔记(一)_卷心菜不卷Iris的博客-CSDN博客 堆参数调优入门 jdk1.7: jdk1.8: 面试题:给定-Xms Xmx -Xmn 问 最大的eden区域是多少M。 常用JVM参数 怎么对jvm进行调优?通过参数配…...
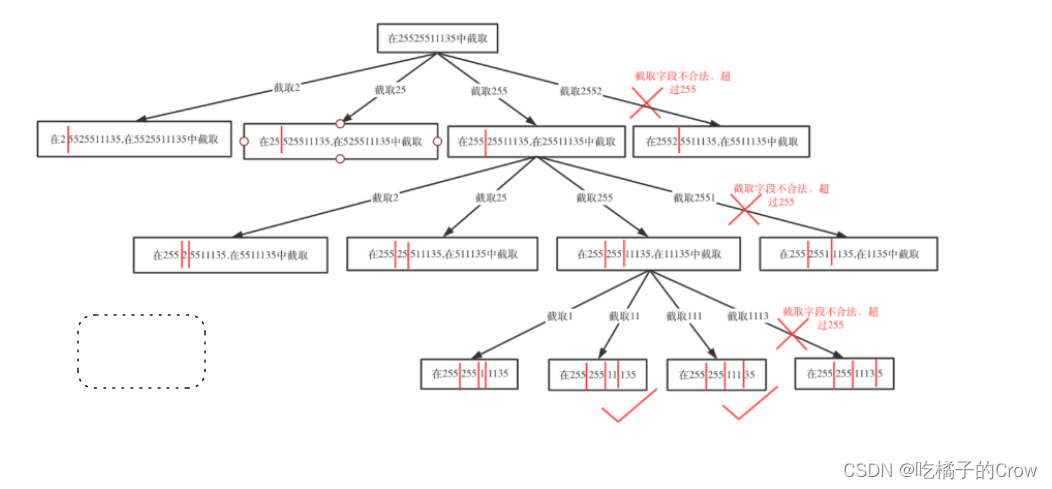
面试热题(复原ip地址)
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 . 分隔。 例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.24…...

【JavaSE】Java方法的使用
【本节目标】 1. 掌握方法的定义以及使用 2. 掌握方法传参 3. 掌握方法重载 4. 掌握递归 目录 1.方法概念及使用 1.1什么是方法(method) 1.2 方法定义 1.3 方法调用的执行过程 1.4 实参和形参的关系 2. 方法重载 2.1 为什么需要方法重载 2.2 方法重载概念 3. 递归 3.…...
)
Node.js 安装和配置(完整详细版)
在Windows上安装和配置Node.js: 下载Node.js安装程序: 前往Node.js官方网站(https://nodejs.org/),在主页上找到"Downloads"(下载)选项。然后选择适用于Windows的"Windows Insta…...
:稀疏训练及剪枝效果展示)
剪枝基础与实战(4):稀疏训练及剪枝效果展示
稀疏训练是通过在损失loss中增加BN的 γ \gamma γ 参数的L1正则,从而让绝大多数通道对应的 γ \gamma γ值趋近与0, 从而使得模型达到稀疏化的效果:...

CentOS 7.6使用yum安装stress,源码安装stree-ng 0.15.06,源码安装sysstat 12.7.2
cat /etc/redhat-release看到操作系统的版本是CentOS Linux release 7.6.1810 (Core),uname -r可以看到内核版本是3.10.0-957.21.3.el7.x86_64 yum install stress sysstat -y安装stress和sysstat。 使用pidstat -u 5 1没有%wait项: 原因是CentOS 7仓…...
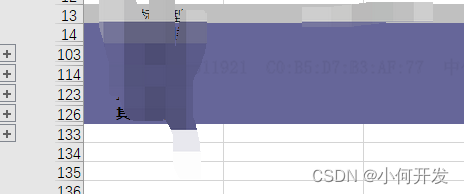
POI groupRow 折叠分组,折叠部分不显示问题
折叠组是什么?如图就是用POI 实现的,代码很简单:sheet.groupRow(开始行,结束行)即可 但是万万没想到,最终实现出的结果,合并的组,有一部分并没有渲染出来,如下图: 因为我…...
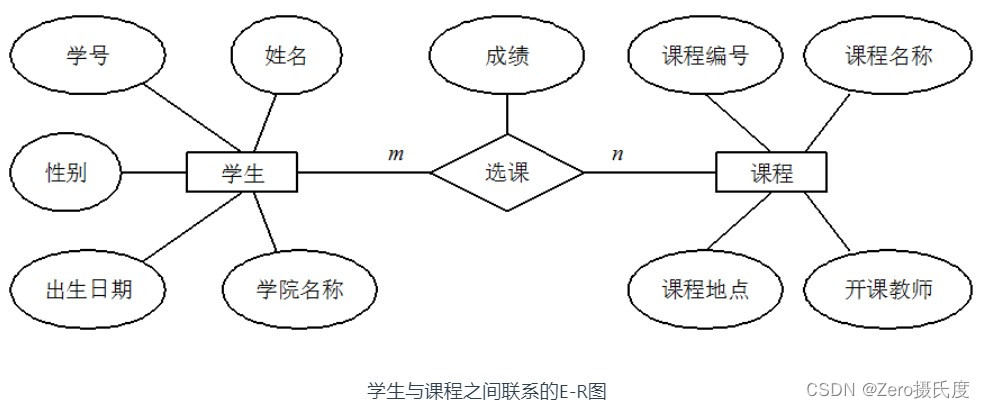
一、数据库基础
数据库 一、数据库基础 1、一些概念 数据库:数据库(DataBase ,简称DB),就是信息的集合。数据库是由数据库管理系统管理的数据的集合;数据库管理系统:简称DBMS 。是一种操纵和管理数据库的大型…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
