LeetCode 面试题 01.05. 一次编辑
文章目录
- 一、题目
- 二、C# 题解
- 法一:从第一个不同位置处判断后续相同子串
- 法二:前后序遍历判断第一个不同字符的位置关系
- 优化
- 法一
- 法二
一、题目
字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串,编写一个函数判定它们是否只需要一次(或者零次)编辑。
点击此处跳转题目。
示例 1:
输入:
first = “pale”
second = “ple”
输出: True
示例 2:
输入:
first = “pales”
second = “pal”
输出: False
二、C# 题解
法一:从第一个不同位置处判断后续相同子串
由题可知,在不同位置处,左方和右方的子串应相同。因此,先寻找到第一个不同的字符,判断其后方子串是否一致:
-
替换:
IsSame(first, i + 1, second, j + 1)
h o r s e ( f i r s t ) i : ↑ h o r t e ( s e c o n d ) j : ↑ \begin{array}{l} & h & o & r & s & e & (first)\\ i:& & & & \uparrow & \\\\ & h & o & r & t & e & (second)\\ j:& & & & \uparrow & \end{array} i:j:hhoorrs↑t↑ee(first)(second) -
插入:
IsSame(first, i, second, j + 1)
h o r s e ( f i r s t ) i : ↑ h o r t s e ( s e c o n d ) j : ↑ \begin{array}{l} & h & o & r & s & e & & (first)\\ i:& & & & \uparrow & \\\\ & h & o & r & t & s & e & (second)\\ j:& & & & \uparrow & \end{array} i:j:hhoorrs↑t↑ese(first)(second) -
删除:
IsSame(first, i + 1, second, j)
h o r s e ( f i r s t ) i : ↑ h o r e ( s e c o n d ) j : ↑ \begin{array}{l} & h & o & r & s & e & (first)\\ i:& & & & \uparrow & \\\\ & h & o & r & e & & (second)\\ j:& & & & \uparrow & \end{array} i:j:hhoorrs↑e↑e(first)(second)
public class Solution {// 方法:从第一个不同位置处判断后续相同子串public bool OneEditAway(string first, string second) {int i = 0, j = 0; // 双指针,i 遍历 first,j 遍历 second(可以用一个指针代替,因为 i 时刻等于 j)// 前序遍历寻找第一处不同while (i < first.Length && j < second.Length) { if (first[i] != second[j]) break;i++; j++;}// 判断字符串相等if (i == first.Length && j == second.Length) return true;// 判断后续内容是否相同return IsSame(first, i + 1, second, j) || IsSame(first, i, second, j + 1) || IsSame(first, i + 1, second, j + 1);}// 判断从位置 i 开始的 first 字符串和从位置 j 开始的 second 字符串是否相等public bool IsSame(string first, int i, string second, int j) {// 判断界限内每个字符是否相等while (i < first.Length && j < second.Length) {if (first[i] != second[j]) return false;i++; j++;}// 判断是否都到达了字符串末尾,避免出现其中一个字符串仍有后续内容的情况return i == first.Length && j == second.Length;}
}
- 时间复杂度: O ( m a x ( m , n ) ) O(max(m,n)) O(max(m,n)),其中 m , n m,n m,n 分别为字符串 f i r s t , s e c o n d first, second first,second 的长度。
- 空间复杂度: O ( 1 ) O(1) O(1)。
法二:前后序遍历判断第一个不同字符的位置关系
使用前序遍历找出两个字符串不同字符的第一个位置 firstDif1, firstDif2,再用后序遍历找出两个字符串不同字符的第一个位置 lastDif1, lastDif2。依据这四个位置的关系来判断字符串的关系:
-
相等:
firstDif1 == first.Length && lastDif1 == -1
至于 firstDif2 == second.Length && lastDif2 == -1 可以不判断,因为必定存在。
h o r s e l a s t D i f 1 : ↑ ↑ : f i r s t D i f 1 h o r s e l a s t D i f 2 : ↑ ↑ : f i r s t D i f 2 \begin{array}{l} & & h & o & r & s & e & &\\ lastDif1: & \green\uparrow & & & & & & \red\uparrow & :firstDif1\\\\ & & h & o & r & s & e & &\\ lastDif2: & \green\uparrow & & & & & & \red\uparrow & :firstDif2 \end{array} lastDif1:lastDif2:↑↑hhoorrssee↑↑:firstDif1:firstDif2 -
替换:
firstDif1 == lastDif1 && firstDif2 == lastDif2
h o r s e f i r s t D i f 1 : ↑ ↑ : l a s t D i f 1 h o r t e f i r s t D i f 2 : ↑ ↑ : l a s t D i f 2 \begin{array}{l} & & h & o & r & s & e & &\\ firstDif1: & & & & & \red\uparrow\green\uparrow & & & :lastDif1\\\\ & & h & o & r & t & e & &\\ firstDif2: & & & & & \red\uparrow\green\uparrow & & & :lastDif2 \end{array} firstDif1:firstDif2:hhoorrs↑↑t↑↑ee:lastDif1:lastDif2 -
插入:
firstDif1 - 1 == lastDif1 && firstDif2 == lastDif2
h o r s e l a s t D i f 1 : ↑ ↑ : f i r s t D i f 1 h o r t s e f i r s t D i f 2 : ↑ ↑ : l a s t D i f 2 \begin{array}{l} & & h & o & r & s & e & &\\ lastDif1: & & & & \green\uparrow & \red\uparrow & & & :firstDif1\\\\ & & h & o & r & t & s & e & &\\ firstDif2: & & & & & \red\uparrow\green\uparrow & & & :lastDif2 \end{array} lastDif1:firstDif2:hhoor↑rs↑t↑↑ese:firstDif1:lastDif2 -
删除:
firstDif1 == lastDif1 && firstDif2 - 1 == lastDif2
h o r s e f i r s t D i f 1 : ↑ ↑ : l a s t D i f 1 h o r e l a s t D i f 2 : ↑ ↑ : f i r s t D i f 2 \begin{array}{l} & & h & o & r & s & e & &\\ firstDif1: & & & & & \red\uparrow\green\uparrow & & & :lastDif1\\\\ & & h & o & r & e & &\\ lastDif2: & & & & \green\uparrow & \red\uparrow & & & :firstDif2 \end{array} firstDif1:lastDif2:hhoorr↑s↑↑e↑e:lastDif1:firstDif2
public class Solution {// 前后序遍历判断第一个不同字符的位置关系public bool OneEditAway(string first, string second) {int firstDif1, firstDif2, lastDif1, lastDif2;FirstDiffer(first, out firstDif1, second, out firstDif2);LastDiffer(first, out lastDif1, second, out lastDif2);// 相等if (firstDif1 == first.Length && lastDif1 == -1) return true;// 替换if (firstDif1 == lastDif1 && firstDif2 == lastDif2) return true;// 插入if (firstDif1 - 1 == lastDif1 && firstDif2 == lastDif2) return true;// 删除if (firstDif1 == lastDif1 && firstDif2 - 1 == lastDif2) return true;return false;}// 前序寻找第一个不同字符的位置public void FirstDiffer(string first, out int firstDif1, string second, out int firstDif2) {firstDif1 = firstDif2 = 0;while (firstDif1 < first.Length && firstDif2 < second.Length) {if (first[firstDif1] != second[firstDif2]) return;firstDif1++; firstDif2++;}}// 后序寻找第一个不同字符的位置public void LastDiffer(string first, out int lastDif1, string second, out int lastDif2) {lastDif1 = first.Length - 1;lastDif2 = second.Length - 1;while (lastDif1 >= 0 && lastDif2 >= 0) {if (first[lastDif1] != second[lastDif2]) return;lastDif1--; lastDif2--;}}
}
- 时间复杂度: O ( m a x ( m , n ) ) O(max(m,n)) O(max(m,n)),其中 m , n m,n m,n 分别为字符串 f i r s t , s e c o n d first, second first,second 的长度。
- 空间复杂度: O ( 1 ) O(1) O(1)。
优化
看到了题解中有大佬使用手段确保 first 长度不大于 second,写法很好,借鉴一下。由于此题插入和删除具有对称性,因此可以做出如下优化:
法一
可以不判断删除的情况,减少一次遍历。
public class Solution {public bool OneEditAway(string first, string second) {if (first.Length > second.Length) // 确保 first 长度不大于 secondreturn OneEditAway(second, first);int i = 0, j = 0; while (i < first.Length && j < second.Length) { if (first[i] != second[j]) break;i++; j++;}// 判断字符串相等,只用判断 second 是否达到末端即可if (j == second.Length) return true;// 判断后续内容是否相同,少判断一种情况return IsSame(first, i, second, j + 1) || IsSame(first, i + 1, second, j + 1);}public bool IsSame(string first, int i, string second, int j) {while (i < first.Length && j < second.Length) {if (first[i] != second[j]) return false;i++; j++;}return i == first.Length && j == second.Length;}
}
法二
法二没有必要了,因为减少“删除”的情况,只减少了一次 int 比较的判断,而可能多带来一次参数拷贝(first 和 second 互换传入参数)。
相关文章:

LeetCode 面试题 01.05. 一次编辑
文章目录 一、题目二、C# 题解法一:从第一个不同位置处判断后续相同子串法二:前后序遍历判断第一个不同字符的位置关系 优化法一法二 一、题目 字符串有三种编辑操作:插入一个英文字符、删除一个英文字符或者替换一个英文字符。 给定两个字符串ÿ…...

Mybatis查询in的字段过多不走索引
mybatis查询in的字段有索引,比如说是主键查询, 但是in的字段过多导致索引失效, 这个时候可以考虑将in的数量变少, 200以内都可以, 在数据库方面采用 foreach unionall 的方式将数据集合查询出来 Service层: List<…...
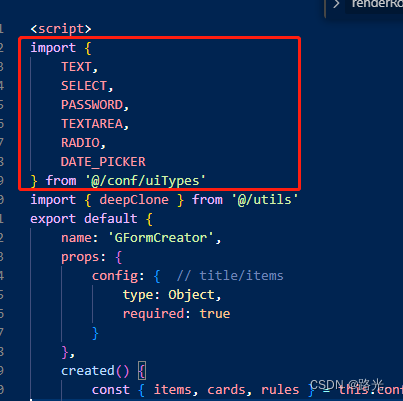
封装公共el-form表单(记录)
1.公共表单组件 //commonForm.vue <script> import {TEXT,SELECT,PASSWORD,TEXTAREA,RADIO,DATE_PICKER } from /conf/uiTypes import { deepClone } from /utils export default {name: GFormCreator,props: {config: { // title/itemstype: Object,required: true}}…...

List 分批处理
1.Google Guava <dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><version>31.0.1-jre</version></dependency>List<String> tempList Arrays.asList("水星","金星&qu…...

SpringSession
Spring Session 是 Spring 的项目之一。Spring Session 提供了一套创建和管理 Servlet HttpSession 的方案,默认采用外置的 Redis 来存储 Session 数据,以此来解决 Session 共享的 问题。(springsession储存session数据的方式有很多,我们常…...

Python Web 开发之 JWT 简介
在之前的课程中,介绍过 Flask-Login 框架,它是基于 Session 和 Cookie 技术来实现用户授权和验证的,不过 Session 有很多的局限性,这一节介绍一种基于 token 的验证方式 —— JWT (JSON Web Token),除了对 JWT 的概念讲解之外&…...

科技资讯|荷兰电动自行车丢失将被拒保,苹果Find My可以减少丢失
荷兰最大的自行车协会荷兰皇家旅游俱乐部宣布,将不再为胖胎电动自行车提供保险,因为这种自行车的被盗风险极高。 随着电动自行车的销量飙升,胖胎也变得更受欢迎。但问题是,胖胎电动自行车也成为了自行车盗窃者的首选目标。ANWB …...

debian rules语法
当创建Debian软件包时,debian/rules 文件是非常重要的,它定义了软件包的构建规则。这个文件使用Makefile语法,指导构建、编译和安装软件包。下面将详细地介绍debian/rules文件的语法和常见用法。 基本结构: 一个简单的debian/rul…...
网易2023年Q2财报:营收240亿元,游戏技术跨产业创造数字就业
8月24日,网易发布2023年Q2财报。二季度,网易继续聚焦主营业务,业绩表现稳健;净收入240亿元,非公认会计准则下归属于公司股东的持续经营净利润90亿元,研发投入39亿元,相当于拿出近一半利润投入研…...

Python的Flask框架创建、运行与访问
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

Java课题笔记~ 综合案例
3.综合案例 3.1 功能介绍 以上是我们在综合案例要实现的功能。除了对数据的增删改查功能外,还有一些复杂的功能,如 批量删除、分页查询、条件查询 等功能 批量删除 功能:每条数据前都有复选框,当我选中多条数据并点击 批量删除 按…...
Seaborn数据可视化(二)
目录 1.Seaborn风格设置 1.1 主题设置 1.2 轴线设置 1.3 移除轴线 1.4 使用字典传递函数 2.设置绘图元素比例 2.1 设置绘图元素比例paper 2.2 设置绘图元素比例poster 2.3 设置绘图元素比例notebook Seaborn将Matplotlib的参数划分为两个独立的组合,第一组用于…...
)
HDLBits-Verilog学习记录 | Verilog Language-Basics(1)
文章目录 3.Simple wire4.Four wires5.inverter | Notgate6. And gate7.Nor gate8.Xnorgate 3.Simple wire problem:Create a module with one input and one output that behaves like a wire. module top_module( input in, output out );assign out in;endmodule4.Four w…...

elementui表格嵌套上传文件直传到oss服务器(表单上传)
提示:记录项目中遇到的问题,仅供参考 文章目录 前言一、vue代码二、js接口请求代码 前言 项目需求是在表格中嵌套一个上传图片的功能,并且回显选择的图片和已上传的图片,再通过点击操作列中上传按钮才开始上传,使用的…...

使用navicat来访问doris
访问Doris的UI http:// dorisfe_ip:8030 由于doris是使用mysql协议,因此可以不用任何额外配置就可以使用navicat访问doris。 可以使用MySql客户端来连接Doris FE,也可以使用mysql命令工具连接,因为他是Mysql协议,所以在使用上跟M…...

2023国赛数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...

redis实战-缓存三剑客穿透击穿雪崩解决方案
缓存穿透 定义 缓存穿透 :缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,这样缓存永远不会生效,这些请求都会打到数据库,造成数据库压力,也让缓存没有发挥出应有的作用 解决方案 缓存空对象 当我们客户端…...
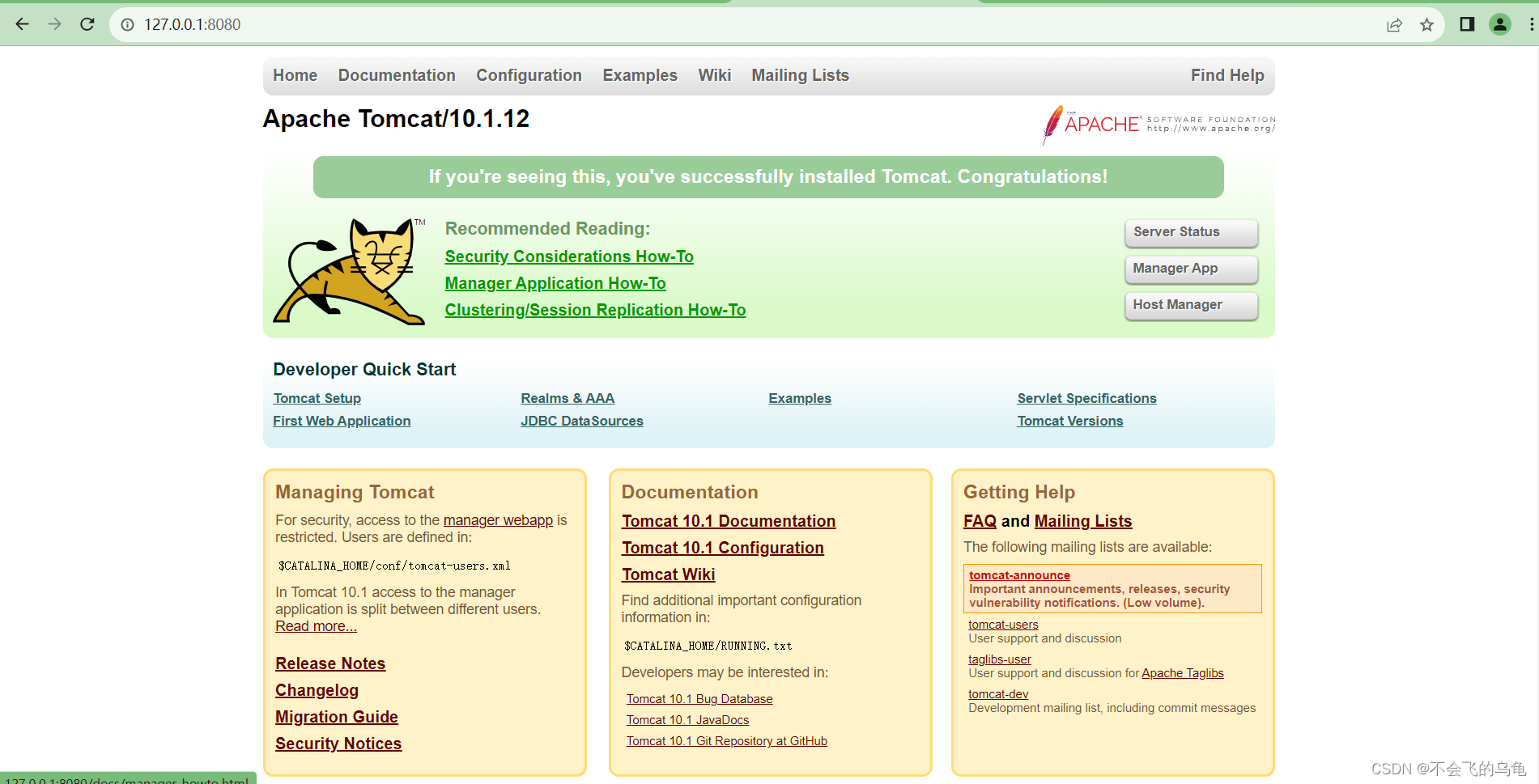
Tomcat10安装及配置教程win11
Tomcat10安装及配置教程win11 Tomcat下载链接 Tomcat官网 Tomcat官网地址 https://tomcat.apache.org/ Tomcat的版本列表 点击上图中左侧红框内**Which version?**即可得下图 下载Tomcat 点击上图中左侧红框内红框内tomcat版本即可得下图,下载zip包 解压zip包…...

遗传算法解决TSP问题
一、求解问题概述 1.1 TSP问题 TSP问题是指旅行商问题(Traveling Salesman Problem)。在TSP问题中,假设有一名旅行商要在给定的一组城市之间进行旅行,每个城市只能被访问一次,并且旅行商必须最终返回出发城市。问题的…...
设计模式-工厂设计模式
核心思想 在简单工厂模式的基础上进一步的抽象化具备更多的可扩展和复用性,增强代码的可读性使添加产品不需要修改原来的代码,满足开闭原则 优缺点 优点 符合单一职责,每个工厂只负责生产对应的产品符合开闭原则,添加产品只需添…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
