动态规划之0-1背包问题
动态规划之0-1背包问题
文章目录
- 动态规划之0-1背包问题
- 一、先给出代码
- 二、讲解
- 第一步:初始化
- 第二步:动态规划,填表
- 第三步:回溯,找到选择方案
- 总结
- 三、进阶(用一维数组解决问题)
一、先给出代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void Bp(vector<int >&weights, vector<int> &values, vector<vector<int>>& dp,int bag_weight,vector<int>&result)
{//初始化for (int j = weights[0]; j <= bag_weight; j++) {dp[0][j] = values[0];}//动态规划,填表//因为第一行是要单独初始化的,后面还要建立在第一行的基础上,所以i初始值为1for (int i = 1; i < weights.size(); i++) {for (int j = 0; j <= bag_weight; j++) {//第一种情况,第i个物品就算单独放也不行;第二种情况,拿上一个没i的结果和有i的比较if (j < weights[i]) {dp[i][j] = dp[i - 1][j];}else {dp[i][j] = max(dp[i - 1][j], dp[i-1][j-weights[i]] + values[i]);}}}//统计拿走的东西种类for (int i = weights.size() - 1, j = bag_weight; i > 0; i--) {if (dp[i][j] > dp[i - 1][j]) {result.push_back(i);j -= weights[i];}if (i == 1 && dp[i][j] !=values[i]) {//如果dp[1][j]的不等于values[1]result.push_back(0);}}
}int main()
{int num,weight, value,bag_weight;vector <int> weights ;vector<int> values ;vector<int>result;cout << "Please enter the number of weights and values!" << endl;//输入东西种类数量cin >> num;//分别输入重量和价值cout << "Please enter the weights! " << endl;for (int i = 0; i < num;i++) {cin >> weight;weights.push_back(weight);}cout << "Please enter the values!" << endl;for (int i = 0; i < num; i++) {cin >> value;values.push_back(value);}cout << "Please enter the weight of bag!" << endl;cin>> bag_weight ;vector<vector<int>> dp(weights.size() + 1, vector<int>(bag_weight + 1, 0));Bp(weights,values,dp,bag_weight,result);//输出总额和拿走的东西种类cout <<"The total prize is :" << dp[weights.size() - 1][bag_weight] << endl;cout << "The way of result is :" << endl;for (auto it = result.rbegin(); it != result.rend();it++) {cout << *it << " ";}return 0;
}
二、讲解
关于dp数组:
**dp[i][j]表示在考虑前i个物品,并且背包容量为j的情况下,能够获得的最大价值。**这样的一个二维数组可以用来记录不同状态下的最优解,其中i表示物品的编号(从0开始),j表示背包的容量。根据题目的要求,我们希望找到dp[weights.size() - 1][bag_weight],即在考虑所有物品,且背包容量为bag_weight的情况下,能够获得的最大价值。
第一步:初始化
for (int j = weights[0]; j <= bag_weight; j++) {dp[0][j] = values[0];
}
在动态规划中,我们通常需要构建一个状态转移表格(dp数组)来记录状态的变化,在01背包问题中,我们有两个状态:背包容量和物品编号。这里的代码初始化了第一行,表示只有第一个物品时,对于不同背包容量的情况下,能够获得的最大价值。这是一个边界条件,因为只有一个物品,所以它要么放入背包,要么不放入,所以只有当背包容量大于等于第一个物品的重量时,才能将其放入背包,获得对应的价值。
第二步:动态规划,填表
for (int i = 1; i < weights.size(); i++) {for (int j = 0; j <= bag_weight; j++) {if (j < weights[i]) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);}}
}
这部分代码构建了整个dp数组。在这里,我们逐步考虑每个物品,以及在不同背包容量下获得的最大价值。对于每个物品,我们有两个选择:放入背包或者不放入背包。每个单元格dp[i][j]的值是根据以下两种情况来确定的:
- 如果第i个物品的重量
weights[i]大于当前背包容量j,那么不能将第i个物品放入背包,所以最大价值与上一个状态dp[i-1][j]相同。 - 如果第i个物品的重量
weights[i]小于等于当前背包容量j,那么我们有两种选择:放入第i个物品或者不放入。我们需要比较这两种选择对应的最大价值,选择其中较大的值作为dp[i][j]的值。
第三步:回溯,找到选择方案
for (int i = weights.size() - 1, j = bag_weight; i > 0; i--) {if (dp[i][j] > dp[i - 1][j]) {result.push_back(i);j -= weights[i];}if (i == 1 && dp[i][j] != values[i]) {result.push_back(0);}
}
这部分代码用于回溯,找出实际选择了哪些物品放入背包,从而达到最大价值。从dp数组的右下角(即dp[weights.size() - 1][bag_weight])开始,我们倒退遍历dp数组。如果发现当前位置的最大价值与上一行相同,说明当前物品没有放入背包,我们直接跳到上一行;如果不同,说明当前物品放入了背包,我们将其记录在result中,并将背包容量减去该物品的重量,然后继续向上遍历。还有一种额外情况,就是如果在遍历到第一个物品时,背包容量还有剩余,且最终的最大价值不等于第一个物品的价值,说明第一个物品也被放入了背包。
总结
这个算法的思路是通过动态规划解决01背包问题。它从初始状态出发,通过填充dp数组来逐步构建出最优解。然后通过回溯,找出实际的选择方案。在动态规划的过程中,关键在于将问题分解为子问题,通过比较不同选择来得出最优解,最终获得整体的最优解。
三、进阶(用一维数组解决问题)
我们创建了一个一维向量 dp,其中 dp[i] 表示在背包容量为 i 时可以达到的最大总价值。这个向量的长度是 bag_Weight + 1,因为背包的容量从0到bag_Weight。
现在让我们来思考动态规划的递推过程。我们要从第一个物品开始,逐步考虑加入更多的物品,直到考虑完所有物品。为了实现这个过程,我们使用了两个嵌套的循环。外层循环遍历所有的物品,内层循环遍历从背包的最大承重开始,逐步减少背包的容量。
在内层循环中,我们要考虑两种情况:放入当前物品和不放入当前物品。我们通过比较这两种情况来决定背包在当前容量下的最优解。具体来说,如果当前物品的重量不超过背包的当前容量(即 j >= weight[i]),我们就可以尝试放入这个物品,然后在背包剩余容量为 j - weight[i] 时找到前一个状态的最优解,加上当前物品的价值。这个过程保证了在考虑前 i 个物品的情况下,背包容量为 j 的最优解。
在比较放入和不放入当前物品的情况后,我们将较大的值赋给 dp[j],表示背包容量为 j 时的最大总价值。这个过程通过逐渐增加物品数量和背包容量,使得我们可以在最终考虑完所有物品时,得到背包的最优解。
最终,当我们完成外层和内层循环后,dp[bag_Weight] 就存储了问题的最终解,即背包的最大总价值。我们输出这个值,就完成了整个过程。
为什么for循环外层遍历物品,而内层遍历重量?
- 外层循环遍历物品(
i的变化): 当我们考虑第i个物品时,我们已经考虑了前i-1个物品的情况,假设这些子问题的解已经计算出来并存储在dp数组中。外层循环在不同的i值下,使得我们能够逐个考虑每个物品,并在dp数组中记录之前子问题的解。- 内层循环遍历背包容量(
j的变化): 对于每个物品i,我们需要考虑在背包容量从bagWeight逐渐减少到 0 的过程中,如何得到最大总价值。这是因为我们希望逐步填充dp数组中更大的背包容量,依赖于之前较小容量下的最优解。通过从bagWeight减少到 0 的循环顺序,我们可以确保在计算当前背包容量j下的最优解时,之前的更小容量下的解已经计算出来。
#include<iostream>
using namespace std;
#include <vector>
void Bp() {vector<int> weight = { 1, 3, 4 };vector<int> value = { 15, 20, 30 };int bag_Weight = 4;vector<int> dp(bag_Weight + 1, 0);for (int i = 0; i < value.size(); i++) {for (int j = bag_Weight; j >= weight[i]; j--) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bag_Weight] << endl;
}int main() {Bp();
}
相关文章:

动态规划之0-1背包问题
动态规划之0-1背包问题 文章目录 动态规划之0-1背包问题一、先给出代码二、讲解第一步:初始化第二步:动态规划,填表第三步:回溯,找到选择方案总结 三、进阶(用一维数组解决问题) 一、先给出代码…...
为什么需要单元测试?
为什么需要单元测试? 从产品角度而言,常规的功能测试、系统测试都是站在产品局部或全局功能进行测试,能够很好地与用户的需要相结合,但是缺乏了对产品研发细节(特别是代码细节的理解)。 从测试人员角度而言…...
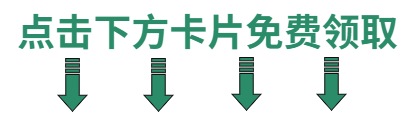
《合成孔径雷达成像算法与实现》Figure3.13——匹配滤波器的三种实现方式
clc clear close all% 参数设置 TBP 80; % 时间带宽积 T 10e-6; % 脉冲持续时间 N_ZD 60; % 零频点位于中点右侧的距离,P58% 参数计算 B TBP/T; …...
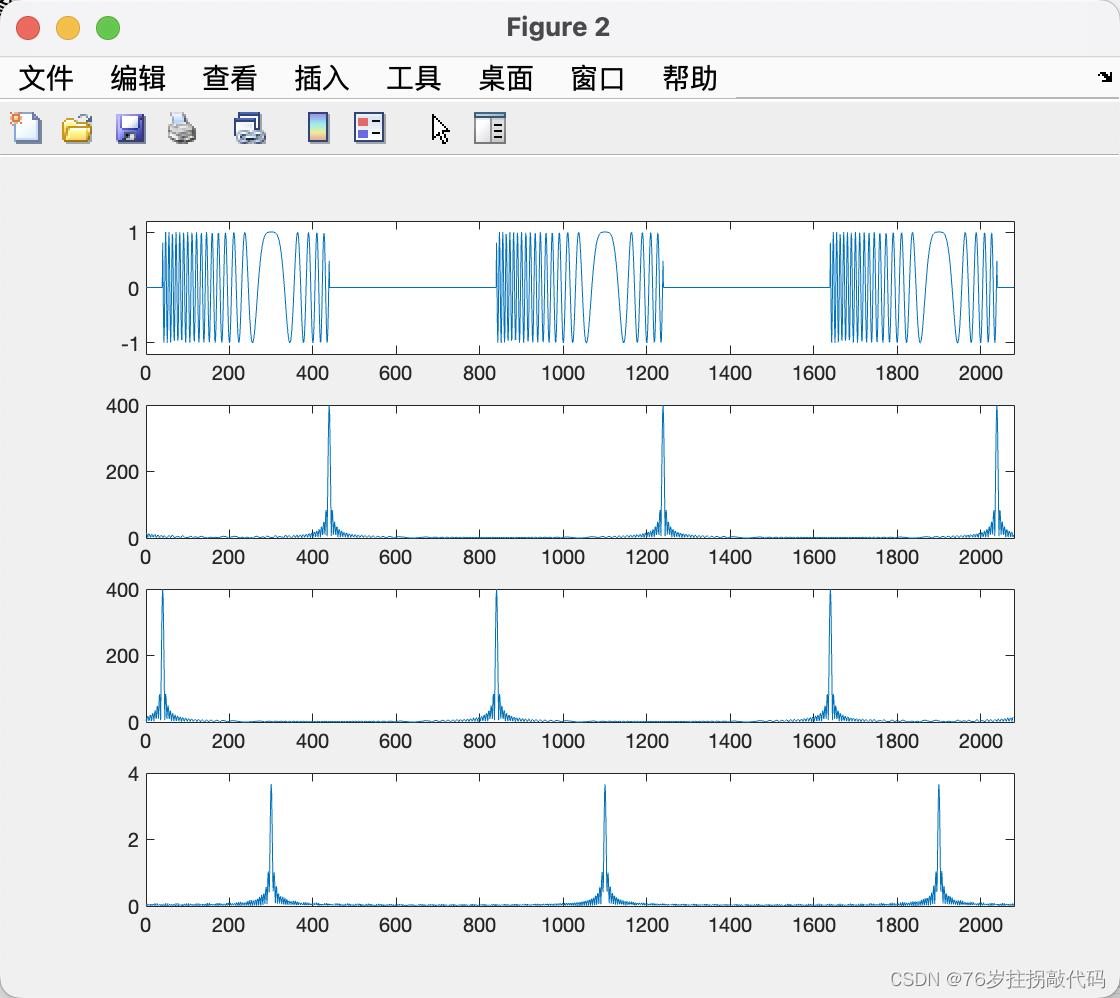
Android企业项目开发实训室建设方案
一 、系统概述 Android企业项目开发作为新一代信息技术的重点和促进信息消费的核心产业,已成为我国转变信息服务业的发展新热点:成为信息通信领域发展最快、市场潜力最大的业务领域。互联网尤其是移动互联网,以其巨大的信息交换能力和快速渗透…...

11_Redis经典五大类型源码及底层实现
Redis经典五大类型源码及底层实现 一、Redis数据类型的底层数据结构 SDS动态字符串双向链表压缩列表 zpilist哈希表 hashtable调表 skiplist整数集合 intset快速列表 quicklist紧凑列表 listpack 二、Redis源码地址 Github:https://github.com/redis/redis 三、…...

AWS WAF实战、优势对比和缺陷解决
文章目录 挑战和目标AWS WAF的优势AWS WAF的不足我是怎么做的?什么是比较好的AWS WAF设计? 笔者为了解决公司Web站点防御性问题,较为深入的研究AWS WAF的相关规则。面对上千万的冲突,笔者不得设计出一种能漂亮处理冲突数据WAF规则。 AWS WAF开发人员在…...

13,【设计模式】代理
代理 代理支持任意参数的简单代理实现 代理 代理的本质是函数指针 代理分为单播,多播,动态多播(ue4中提出的) 单播:在网络通信中,单播是一种一对一的通信方式 多播:在网络通信中,…...
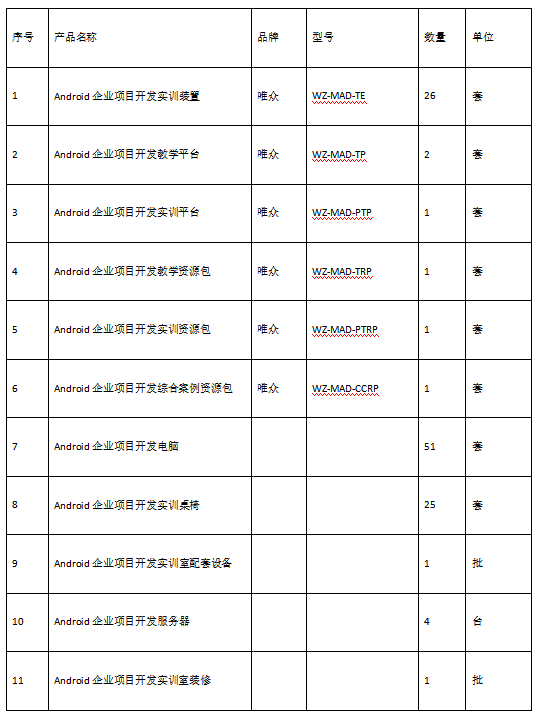
基于IDEA使用maven创建hibernate项目
1、创建maven项目 2、导入hibernate需要的jar包 <!--hibernate核心依赖--><dependency><groupId>org.hibernate</groupId><artifactId>hibernate-core</artifactId><version>5.4.1.Final</version></dependency><!--…...

使用Termux在安卓手机上搭建Hexo博客网站,并发布到公网访问
文章目录 1. 安装 Hexo2. 安装cpolar内网穿透3. 公网远程访问4. 固定公网地址 Hexo 是一个用 Nodejs 编写的快速、简洁且高效的博客框架。Hexo 使用 Markdown 解析文章,在几秒内,即可利用靓丽的主题生成静态网页。 下面介绍在Termux中安装个人hexo博客并…...

宝塔 杀死 java服务 netstat -tlnp | grep :7003 kill 2205698
7003 是端口 netstat -tlnp | grep :7003 kill 2205698...

Python3 数据类型转换
Python3 数据类型转换 有时候,我们需要对数据内置的类型进行转换,数据类型的转换,一般情况下你只需要将数据类型作为函数名即可。 Python 数据类型转换可以分为两种: 隐式类型转换 - 自动完成显式类型转换 - 需要使用类型函数来…...

Cookie 和 Session 的工作流程
目录 一、Cookie是什么? 二、Session是什么? 三、Cookie的工作流程 四、Session的工作流程 五、Session和Cookie的区别和联系 一、Cookie是什么? Cookie是一种在网站和用户之间交换信息的机制。它是由Web服务器发送给用户浏览器的小型文本文件ÿ…...
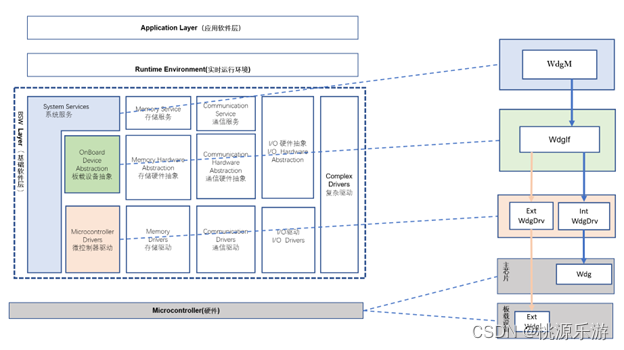
AutoSAR配置与实践(基础篇)3.6 BSW的WatchDog功能
3.6 BSW的WatchDog功能 一、WatchDog功能介绍1.1 WatchDog 模块组成1.2 内外部看门狗区别和原理1.3 常见看门狗校验方式一、WatchDog功能介绍 1.1 WatchDog 模块组成 WatchDog 即看门狗功能。这个看门狗不是真正看家的狗,而是软件的一个模块,但是因为功能类似故以此起名。主…...

运维高级第6次作业
1.安装docker服务,配置镜像加速器 Docker安装与镜像加速器配置_ZRSAI的博客-CSDN博客 2.下载系统镜像(Ubuntu、 centos) 执行该命令后,Docker会自动从Docker Hub镜像库中下载Ubuntu镜像,并将其保存到本地计算机上: [ro…...
)
MongoDB使用GridFS存储大数据(Java)
MongoDB 是一个灵活的 NoSQL 数据库,能够存储大量的数据。但是,当涉及到特别大的数据项,比如大文件、视频或大型图片时,MongoDB 提供了一个特殊的方法来存储这些数据:GridFS。 简介: 1. 什么是 GridFS&am…...
内网穿透实战应用-windwos10系统搭建我的世界服务器,内网穿透实现联机游戏Minecraft
文章目录 1. Java环境搭建2.安装我的世界Minecraft服务3. 启动我的世界服务4.局域网测试连接我的世界服务器5. 安装cpolar内网穿透6. 创建隧道映射内网端口7. 测试公网远程联机8. 配置固定TCP端口地址8.1 保留一个固定tcp地址8.2 配置固定tcp地址 9. 使用固定公网地址远程联机 …...

pytorch基于ray和accelerate实现多GPU数据并行的模型加速训练
在pytorch的DDP原生代码使用的基础上,ray和accelerate两个库对于pytorch并行训练的代码使用做了更加友好的封装。 以下为极简的代码示例。 ray ray.py #codingutf-8 import os import sys import time import numpy as np import torch from torch import nn im…...
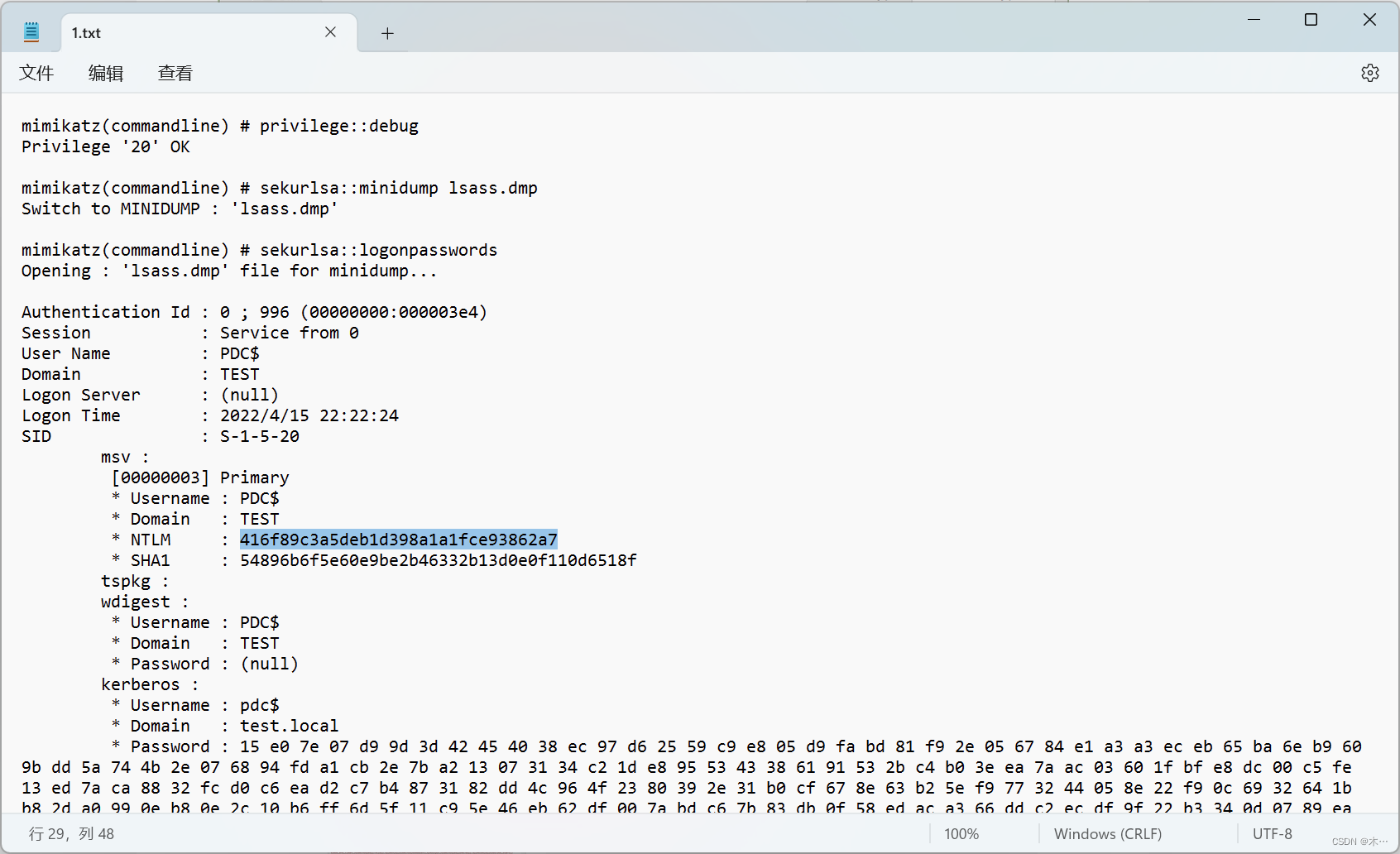
[蓝帽杯 2022 初赛]domainhacker
打开流量包,追踪TCP流,看到一串url编码 放到瑞士军刀里面解密 最下面这一串会觉得像base64编码 删掉前面两个字符就可以base64解码 依次类推,提取到第13个流,得到一串编码其中里面有密码 导出http对象 发现最后有个1.rar文件 不出…...

在 Pytorch 中使用 TensorBoard
机器学习的训练过程中会产生各类数据,包括 “标量scalar”、“图像image”、“统计图diagram”、“视频video”、“音频audio”、“文本text”、“嵌入Embedding” 等等。为了更好地追踪和分析这些数据,许多可视化工具应运而生,比如之前介绍的…...

Grafana Dashboard 备份方案
文章目录 Grafana Dashboard 备份方案引言工具简介支持的组件要求配置备份安装使用 pypi 安装grafana备份工具配置环境变量使用Grafana Backup Tool 进行备份恢复备份 Grafana Dashboard恢复 Grafana Dashboard结论Grafana Dashboard 备份方案 引言 每个使用 Grafana 的同学都…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
