【优选算法】—— 字符串匹配算法
在本期的字符串匹配算法中,我将给大家带来常见的两种经典的示例:
- 1、暴力匹配(BF)算法
- 2、KMP算法
目录
(一)暴力匹配(BF)算法
1、思想
2、演示
3、代码展示
(二)KMP算法
1、思想
2、演示
1️⃣ BF和KMP的区别
2️⃣ K 的值求解
3️⃣ 求next数组的练习
3、代码展示
4、next数组的优化
(三)总结
(一)暴力匹配(BF)算法
1、思想
- 就是将目标串S的第一个字符与模式串T 的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;
- 若不相等,则比较S的第二个字符和 T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。
2、演示
大家看到上诉这段话时肯定是晦涩难懂的,需要例子支持
- 假定我们给出字符串 ”ababcabcdabcde”作为主串, 然后给出子串: ”abcd”;
- 现在我们需要查找子串是否在主串中出现,出现返回主串中的第一个匹配的下标,失败返回-1

- 只要在匹配的过程当中,匹配失败,那么:i回退到刚刚位置的下一个,j回退到0下标重新开始

3、代码展示
int BF(char *str,char *sub) //str:主串 sub:子串
{assert(str != NULL && sub != NULL);if(str == NULL || sub == NULL){return -1;}int i = 0;int j = 0;int strLen = strlen(str);int subLen = strlen(sub);while(i < strLen && j < subLen){if(str[i] == sub[j]){i++;j++;}else{//回退i = i-j+1;j = 0;}}if(j >= subLen){return i-j;}return -1;
}
int main()
{printf("%d\n",BF("ababcabcdabcde","abcd"));printf("%d\n",BF("ababcabcdabcde","abcde"));printf("%d\n",BF("ababcabcdabcde","abcdef"));return 0;
}(二)KMP算法
1、思想
2、演示
1️⃣ BF和KMP的区别

j 的回退位置

💨 针对上述这样的情况,我们就需要引出next数组
2️⃣ K 的值求解
- 1、规则:找到匹配成功部分的两个相等的真子串(不包含本身),一个以下标 0 字符开始,另一个以 j-1 下标字符结尾。
- 2、不管什么数据 next[0] = -1;next[1] = 0;在这里,我们以下标来开始,而说到的第几个第几个是从 1 开始
3️⃣ 求next数组的练习

到这里大家对如何求next数组应该问题不大了,接下来的问题就是,已知next[i] = k;怎么求next[i+1] = ?
- 首先假设: next[i] = k 成立,那么,就有这个式子成立: P0...Pk-1 = Px...Pi-1;得到: P0...Pk-1 = Pi-k..Pi-1;
- 到这一步:我们再假设如果 Pk = Pi;我们可以得到 P0...Pk = Pi-k..Pi;那这个就是 next[i+1] = k+1;

那么: Pk != Pi 呢?

3、代码展示
void GetNext(int *next,const char *sub)
{int lensub = strlen(sub);next[0] = -1;next[1] = 0;int i = 2;//下一项int k = 0;//前一项的Kwhile(i < lensub)//next数组还没有遍历完{if((k == -1) || sub[k] == sub[i-1]){next[i] = k+1;i++;k++;//k = k+1???//下一个K的值新的K值}else{k = next[k];}}
}int KMP(const char *s,const char *sub,int pos)
{int i = pos;int j = 0;int lens = strlen(s);int lensub = strlen(sub);int *next = (int *)malloc(lensub*sizeof(int));//和子串一样长assert(next != NULL);GetNext(next,sub);while(i < lens && j < lensub){if((j == -1) || (s[i] == sub[j])){i++;j++;}else{j = next[j];}}free(next);if(j >= lensub){return i-j;}else{return -1;}
}int main()
{char *str = "ababcabcdabcde";char *sub = "abcd";printf("%d\n",KMP(str,sub,0));return 0;
}4、next数组的优化
- aaaaaaaab;
- next 数组是-1,0,1,2,3,4,5,6,7
练习模式串 t=‘abcaabbcabcaabdab’ ,该模式串的 next 数组的值为( D ) , nextval 数组的值为 ( F )A . 0 1 1 1 2 2 1 1 1 2 3 4 5 6 7 1 2B . 0 1 1 1 2 1 2 1 1 2 3 4 5 6 1 1 2C . 0 1 1 1 0 0 1 3 1 0 1 1 0 0 7 0 1D . 0 1 1 1 2 2 3 1 1 2 3 4 5 6 7 1 2E . 0 1 1 0 0 1 1 1 0 1 1 0 0 1 7 0 1F . 0 1 1 0 2 1 3 1 0 1 1 0 2 1 7 0 1

(三)总结
BF(Brute Force)和KMP(Knuth-Morris-Pratt)算法是两种字符串匹配算法,它们的主要区别在于匹配过程中的策略和效率。
-
BF算法:
- BF算法是一种简单直接的字符串匹配算法,也被称为朴素算法。
- 它的思想是从主串中的每个位置开始,逐个比较主串和模式串的字符,直到找到匹配或遍历完所有可能位置。
- 当字符不匹配时,BF算法通过移动主串指针,重新从下一个位置开始匹配。
- BF算法的时间复杂度为O(m*n),其中m为主串长度,n为模式串长度,最坏情况下需要遍历所有可能的匹配位置。
- 由于BF算法每次只移动一位,对于大规模文本匹配效率较低。
-
KMP算法:
- KMP算法是一种高效的字符串匹配算法,通过利用已知信息减少不必要的字符比较次数。
- 它利用模式串自身的特性,在匹配过程中跳过一部分已经匹配的字符,从而提高匹配效率。
- KMP算法包括两个主要步骤:构建最长公共前后缀数组(next数组)和匹配过程。
- 最长公共前后缀数组(next数组)记录了模式串中对于每个位置,匹配失败时应该跳过的字符数。
- 在匹配过程中,当字符不匹配时,KMP算法通过查询next数组获取跳跃位置,而不是重新从头开始比较。
- KMP算法的时间复杂度为O(m+n),其中m为主串长度,n为模式串长度,通过next数组的优化,可以在匹配过程中跳过一定数量的比较,从而提高效率。
以下是关于上述两种算法的小结:
- 总结起来,BF算法是一种简单直接的字符串匹配算法,逐个比较字符并逐位移动,效率较低;
- 而KMP算法是一种高效的字符串匹配算法,通过构建最长公共前后缀数组和跳跃匹配位置,减少不必要的字符比较次数,提高匹配效率。
- 因此,在大规模文本匹配的应用中,KMP算法通常比BF算法更加高效。
相关文章:

【优选算法】—— 字符串匹配算法
在本期的字符串匹配算法中,我将给大家带来常见的两种经典的示例: 1、暴力匹配(BF)算法 2、KMP算法 目录 (一)暴力匹配(BF)算法 1、思想 2、演示 3、代码展示 (二&…...

Docker容器:docker consul的注册与发现及consul-template守护进程
文章目录 一.docker consul的注册与发现介绍1.什么是服务注册与发现2.什么是consul3.docker consul的应用场景4.consul提供的一些关键特性5.数据流向 二.consul部署1.consul服务器(192.168.198.12)(1)建立 Consul 服务启动consul后…...
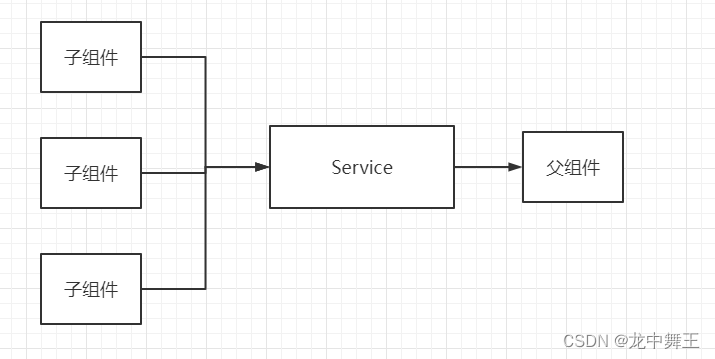
Blazor 依赖注入妙用:巧设回调
文章目录 前言依赖注入特性需求解决方案示意图 前言 依赖注入我之前写过一篇文章,没看过的可以看看这个。 C# Blazor 学习笔记(10):依赖注入 依赖注入特性 只能Razor组件中注入所有Razor组件在作用域注入的都是同一个依赖。作用域可以看看我之前的文章。 需求 …...
)
Python 基础 -- Tutorial(三)
7、输入和输出 有几种方法可以表示程序的输出;数据可以以人类可读的形式打印出来,或者写入文件以备将来使用。本章将讨论其中的一些可能性。 7.1 更花哨的输出格式 到目前为止,我们已经遇到了两种写值的方法:表达式语句和print()函数。(第三种方法是使…...
基于STM32的四旋翼无人机项目(二):MPU6050姿态解算(含上位机3D姿态显示教学)
前言:本文为手把手教学飞控核心知识点之一的姿态解算——MPU6050 姿态解算(飞控专栏第2篇)。项目中飞行器使用 MPU6050 传感器对飞行器的姿态进行解算(四元数方法),搭配设计的卡尔曼滤波器与一阶低通滤波器…...

微信小程序开发教学系列(1)- 开发入门
第一章:微信小程序简介与入门 1.1 简介 微信小程序是一种基于微信平台的应用程序,可以在微信内直接使用,无需下载和安装。它具有小巧、高效、便捷的特点,可以满足用户在微信中获取信息、使用服务的需求。 微信小程序采用前端技…...
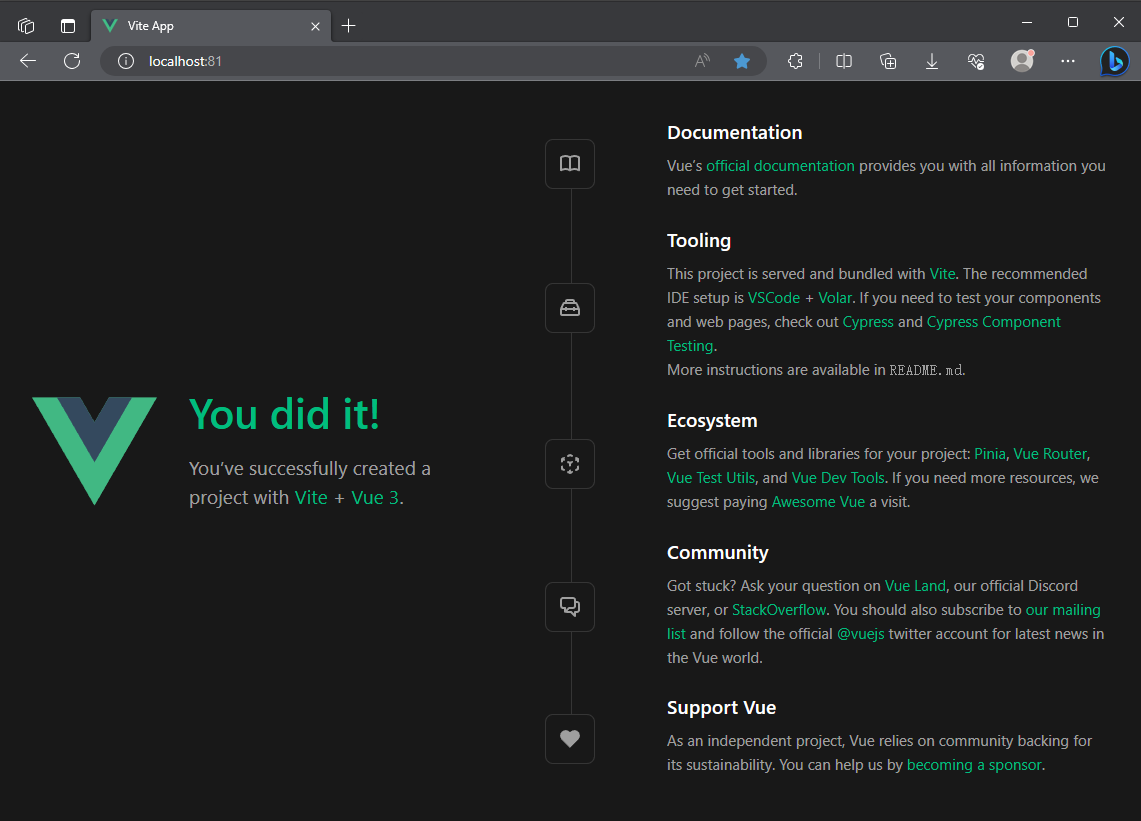
Nginx虚拟主机(server块)部署Vue项目
需求 配置虚拟主机,实现一个Nginx运行多个服务。 实现 使用Server块。不同的端口号,表示不同的服务;同时在配置中指定,Vue安装包所在的位置。 配置 Vue项目,放在 html/test 目录下。 config中的配置如下…...

JAVA开发环境接口swagger-ui使用总结
一、前言 swagger-ui是java开发中生产api说明文档的插件,这是后端工程师和前端工程师联调接口的桥梁。生成的文档就减少了很多没必要的沟通提高开发和测试效率。 二、 swagger-ui的使用 1、引入maven依赖 <dependency><groupId>io.springfox</grou…...

mongodb 数据库管理(数据库、集合、文档)
目录 一、数据库操作 1、创建数据库 2、删除数据库 二、集合操作 1、创建集合 2、删除集合 三、文档操作 1、创建文档 2、 插入文档 3、查看文档 4、更新文档 1)update() 方法 2)replace() 方法 一、数据库操作 1、创建数据库 创建数据库…...

分布式与集群的定义及异同
分布式与集群的定义及异同 分布式定义优点不足 集群优点不足 异同 分布式 定义 分布式是指将一个系统或应用程序分散到多个计算机或服务器上进行处理和管理的技术。它是指多个系统协同合作完成一个特定任务的系统。例如,可以将一个大业务拆分成多个子业务…...

电脑端teams一直在线小程序,简单好用易上手
居家办公的你,会不会想要摸鱼!!会不会想要下楼拿快递!!会不会想要出去下馆子!!!然而,teams的5分钟不操作电脑状态就变为离开大大的阻挡了你幸福生活的脚步!&a…...

YOLOv5算法改进(4)— 添加CA注意力机制
前言:Hello大家好,我是小哥谈。注意力机制是近年来深度学习领域内的研究热点,可以帮助模型更好地关注重要的特征,从而提高模型的性能。在许多视觉任务中,输入数据通常由多个通道组成,例如图像中的RGB通道或…...

无涯教程-PHP - XML GET
XML Get已用于从xml文件获取节点值。以下示例显示了如何从xml获取数据。 Note.xml 是xml文件,可以通过php文件访问。 <SUBJECT><COURSE>Android</COURSE><COUNTRY>India</COUNTRY><COMPANY>LearnFk</COMPANY><PRICE…...
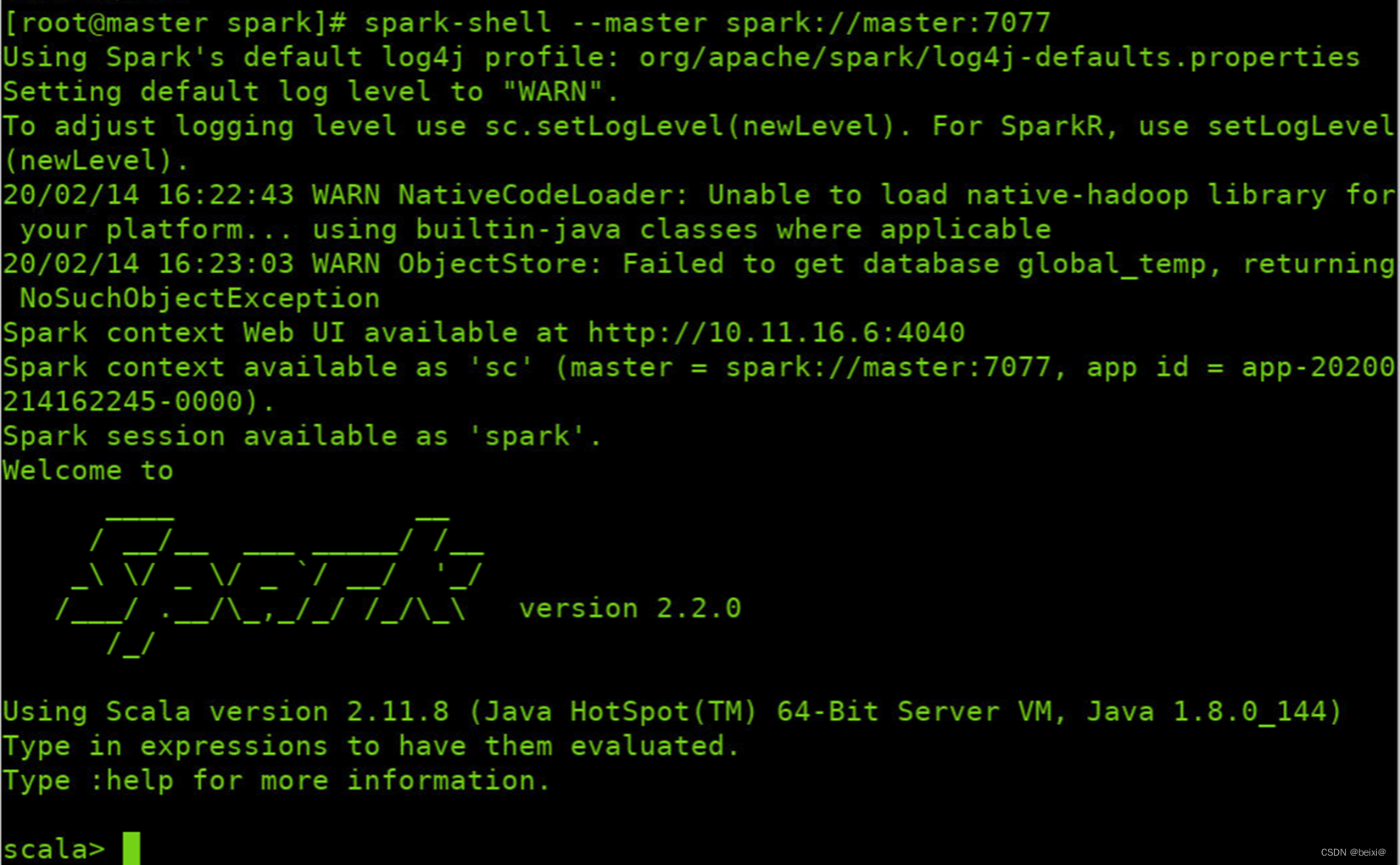
Spark Standalone环境搭建及测试
🥇🥇【大数据学习记录篇】-持续更新中~🥇🥇 篇一:Linux系统下配置java环境 篇二:hadoop伪分布式搭建(超详细) 篇三:hadoop完全分布式集群搭建(超详细…...

【PHP】流程控制-ifswitchforwhiledo-whilecontinuebreak
文章目录 流程控制顺序结构分支结构if分支switch分支 循环结构for循环while循环do-while循环continue和break 流程控制 顺序结构:代码从上往下,顺序执行。(代码执行的最基本结构) 分支结构:给定一个条件,…...

Pytorch-day04-模型构建-checkpoint
PyTorch 模型构建 1、GPU配置2、数据预处理3、划分训练集、验证集、测试集4、选择模型5、设定损失函数&优化方法6、模型效果评估 #导入常用包 import os import numpy as np import torch from torch.utils.data import Dataset, DataLoader from torchvision.transfor…...
使用Xshell7控制多台服务同时安装ZK最新版集群服务
一: 环境准备: 主机名称 主机IP 节点 (集群内通讯端口|选举leader|cline端提供服务)端口 docker0 192.168.1.100 node-0 2888 | 3888 | 2181 docker1 192.168.1.101 node-1 2888 | 388…...

python numpy array dtype和astype类型转换的区别
Python3 本身对整数的支持做了提升,可以支持无限长度的整数:比如: b 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffPython的模块numpy array定义的数组在windows和MACOS上默认长度是…...

浮动属性样式
🍓浮动属性 属性名称中文注释备注float设置盒子浮动left左浮动,right右浮动,none不浮动clear清除浮动left清除左浮动,right清除右浮动,both左右浮动都清除(注意:clear清除浮动一般只有作用在块…...

keepalived双机热备 (四十五)
一、概述 Keepalived 是一个基于 VRRP 协议来实现的 LVS 服务高可用方案,可以解决静态路由出现的单点故障问题。 原理 在一个 LVS 服务集群中通常有主服务器(MASTER)和备份服务器(BACKUP)两种角色的服务器…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
