数据降维 | MATLAB实现T-SNE降维特征可视化
数据降维 | MATLAB实现T-SNE降维特征可视化
目录
- 数据降维 | MATLAB实现T-SNE降维特征可视化
- 降维效果
- 基本描述
- 程序设计
- 参考资料
降维效果
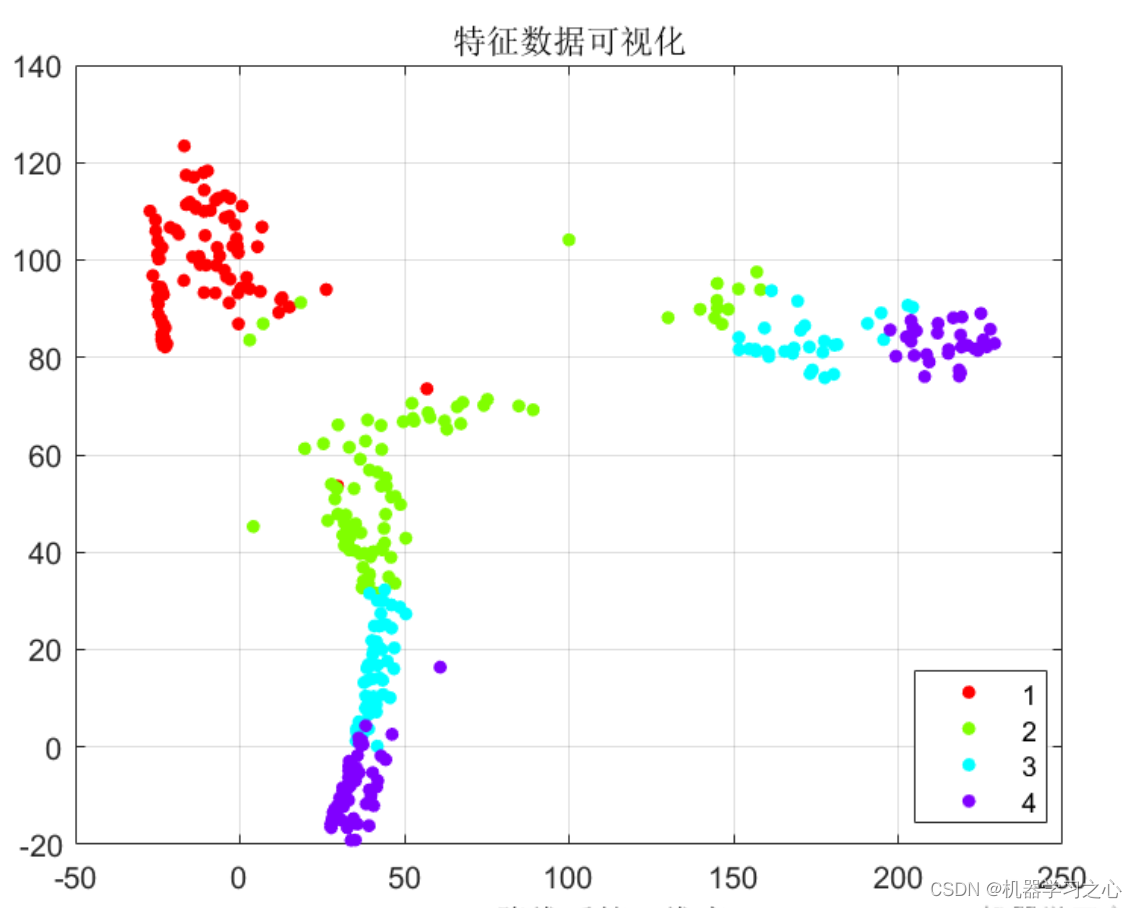
基本描述
T-SNE降维特征可视化,MATLAB程序。
T-分布随机邻域嵌入,主要用途是对高维数据进行降维并进行可视化,以便更好地理解和发现数据之间的结构、模式和聚类关系。它被广泛应用于数据可视化、数据挖掘和机器学习等领域。
包含二维图像和三维图像生成两部分;
EXCEL表格直接导入,更换Excel表格的数据即可。
程序设计
- 完整程序和数据获取方式:私信博主回复MATLAB实现T-SNE降维特征可视化。
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
X1 = sum(p_train, 2);
tSb = tSb - X1 * X1' / num_s - tSw;tSb = (tSb + tSb') / 2;
tSw = (tSw + tSw') / 2;if r == num_d[eigvec, eigval_matrix] = eig(tSb, tSw);
elseopts.disp = 0; [eigvec, eigval_matrix] = eigs(tSb, tSw, r, 'la', opts);
endeigval = diag(eigval_matrix);
[sort_eigval, sort_eigval_index] = sort(eigval);
T0 = eigvec(:, sort_eigval_index(end: -1: 1));
%---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
% 确定嵌入空间中的度量
switch metric% 加权特征向量case 'weighted'T = T0 .* repmat(sqrt(sort_eigval(end: -1: 1))', [num_d, 1]);% 正交归一化case 'orthonormalized'[T, ~] = qr(T0, 0);% 原始特征向量case 'plain'T = T0;
end
————————————————
版权声明:本文为CSDN博主「机器学习之心」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/kjm13182345320/article/details/130454138
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229
相关文章:

数据降维 | MATLAB实现T-SNE降维特征可视化
数据降维 | MATLAB实现T-SNE降维特征可视化 目录 数据降维 | MATLAB实现T-SNE降维特征可视化降维效果基本描述程序设计参考资料 降维效果 基本描述 T-SNE降维特征可视化,MATLAB程序。 T-分布随机邻域嵌入,主要用途是对高维数据进行降维并进行可视化&…...
)
蓝桥杯上岸每日N题 (交换瓶子)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 题目描述 有 N 个瓶子,编号 1∼N,放在架子上。 比如有 5 个瓶子: 2 1 3 5 4 要求每次拿起 2 个瓶子,交换它们的位置。 …...
GMS基本模块TIN、Solids、Modflow2000/2005、MT3DMS、MODPATH。及其在地下水流动、溶质运移、粒子追踪方面的应用
解决地下水数值模拟技术实施过程中遇到的困难,从而提出切实可行的环境保护措施,达到有效保护环境、防治地下水污染,推动经济社会可持续发展的目的。 (1)水文地质学,地下水数值模拟基础理论;&am…...
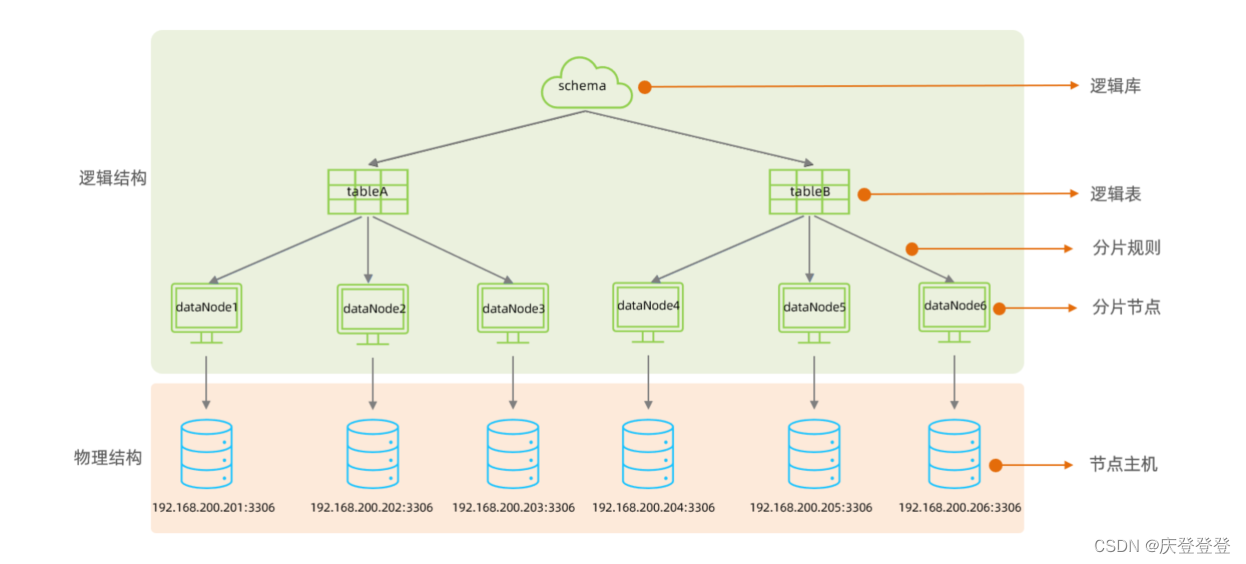
MySQL数据库中间件Mycat介绍及下载安装(教程)
一,介绍 MyCat是开源的、活跃的、基于Java语言编写的MySQL数据库中间件。可以像使用MySQL一样来使用MyCat,对于开发人员来说根本感觉不到MyCat的存在。 开发人员只需要连接MyCat即可,而具体底层用到几台数据库,每一台数据库服务器…...
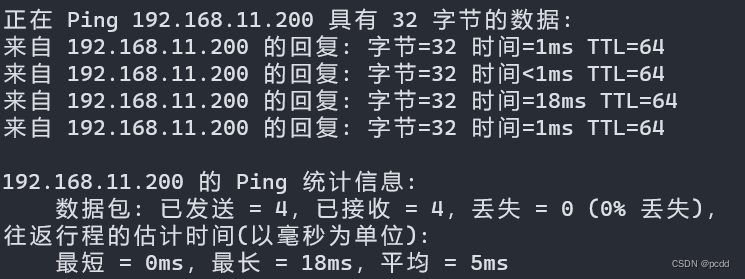
【VMware】CentOS 设置静态IP(Windows 宿主机)
文章目录 1. 更改网络适配器设置2. 配置虚拟网络编辑器3. 修改 CentOS 网络配置文件4. ping 测试结果 宿主机:Win11 22H2 虚拟机:CentOS-Stream-9-20230612.0 (Minimal) 1. 更改网络适配器设置 Win R:control 打开控制面板 依次点击&#x…...
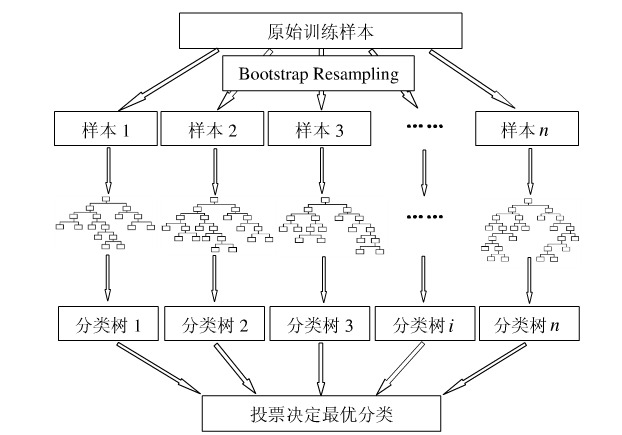
机器学习十大算法之七——随机森林
0 引言 集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据上构建多个横型,集成所有模型的建模结果,基本上所有的机器学习领域都可以看到集成学习…...
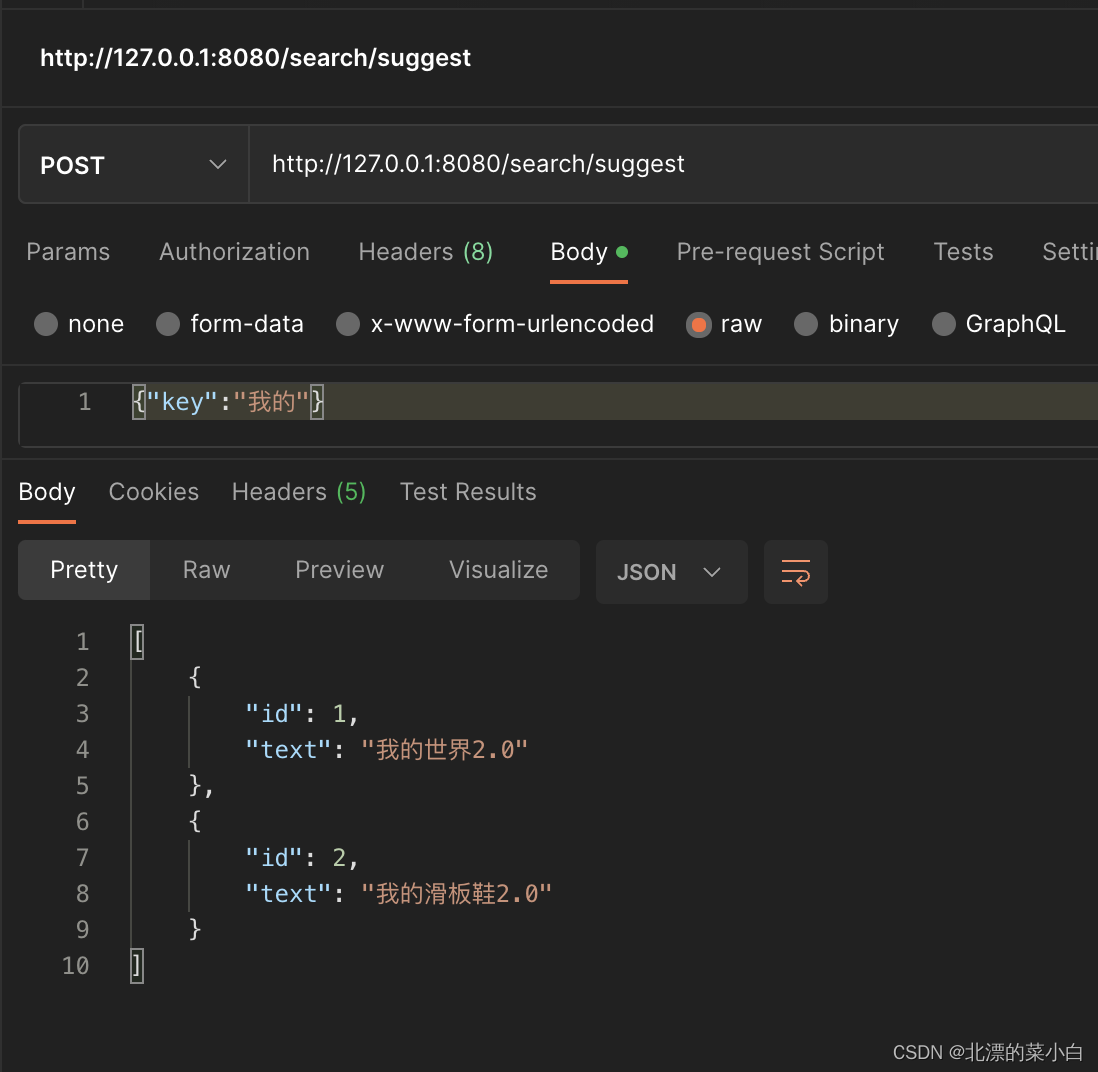
spring boot 3使用 elasticsearch 提供搜索建议
业务场景 用户输入内容,快速返回建议,示例效果如下 技术选型 spring boot 3elasticsearch server 7.17.4spring data elasticsearch 5.0.1elasticsearch-java-api 8.5.3 pom.xml <dependency><groupId>org.springframework.boot</gr…...

住宅IP:解锁更快速、稳定的互联网,你准备好了吗?
随着互联网的广泛普及,我们对网络的需求也越来越高。无论是工作、学习还是娱乐,我们都希望能够享受到更快速、稳定的互联网连接。而在实现这一目标的过程中,住宅IP正逐渐崭露头角,成为了一种备受关注的解决方案。那么,…...

支持dolby vision的盒子接支持dolby vision的电视,在adaptive hdr时,播放非dv的hdr视频,输出sdr
支持dolby vision的盒子接支持dolby vision的电视,setting选择adaptive hdr,按照这个配置在播放非dv的hdr视频时,会输出sdr。 看起来是很不合理的,高级的产品播放高级的片源,却输出低级的画质。 想要搞清楚这个问题&am…...
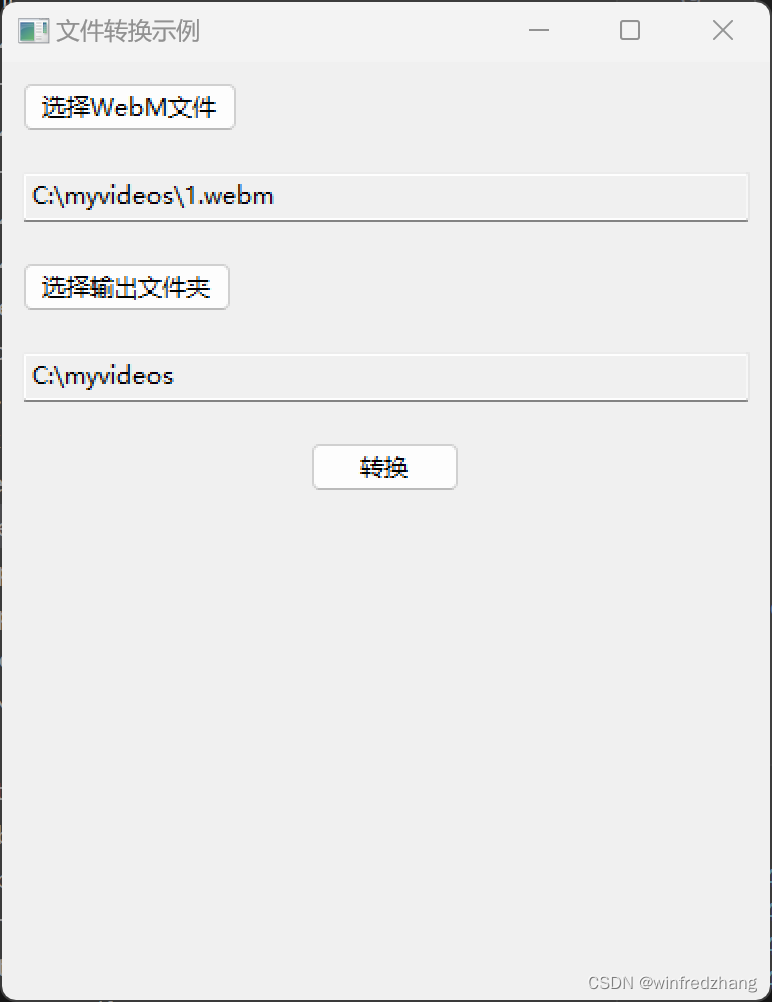
使用ffmpeg将WebM文件转换为MP4文件的简单应用程序
tiktok网上下载的short视频是webm格式的,有些程序无法处理该程序,比如roop程序,本文介绍了如何使用wxPython库创建一个简单的GUI应用程序,用于将WebM文件转换为MP4文件。这个应用程序使用Python编写,通过调用FFmpeg命令…...

Prompt-“设计提示模板:用更少数据实现预训练模型的卓越表现,助力Few-Shot和Zero-Shot任务”
Prompt任务(Prompt Tasks) 通过设计提示(prompt)模板,实现使用更少量的数据在预训练模型(Pretrained Model)上得到更好的效果,多用于:Few-Shot,Zero-Shot 等…...

玩转Mysql系列 - 第6篇:select查询基础篇
这是Mysql系列第6篇。 环境:mysql5.7.25,cmd命令中进行演示。 DQL(Data QueryLanguage):数据查询语言,通俗点讲就是从数据库获取数据的,按照DQL的语法给数据库发送一条指令,数据库将按需求返回数据。 DQ…...
【SpringCloud技术专题】「Gateway网关系列」(1)微服务网关服务的Gateway组件的原理介绍分析
为什么要有服务网关? 我们都知道在微服务架构中,系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢?难道要一个个的去调用吗?很显然这是不太实际的,我们需要有一个统一的接口与这些微服务打交道…...

【面试刷题】————STL中的vector是如何实现的?
STL(Standard Template Library)是C标准库中的一部分,它提供了许多常用的数据结构和算法,其中包括了动态数组 vector。 vector std::vector 是一个动态数组,它能够自动调整自己的大小,以适应存储元素的需…...
)
使用钉钉的扫码会出现多个回调(DTFrameLogin)
官方:地址 标题 出现的问题解决后效果正常使用(按照官网的流程进行使用)自己的理解(路人可忽略该内容!) 出现的问题 1692861955468 解决后效果 1692861665687 正常使用(按照官网的流程进行使用) fn.js 该文件就是钉钉官网的js文件,我下载到了…...

Android | 关于 OOM 的那些事儿
作者:345丶 前言 Android 系统对每个app都会有一个最大的内存限制,如果超出这个限制,就会抛出 OOM,也就是Out Of Memory 。本质上是抛出的一个异常,一般是在内存超出限制之后抛出的。最为常见的 OOM 就是内存泄露(大量…...

珠玑妙算游戏
珠玑妙算游戏,OJ练习 一、描述二、方法一三、方法二 一、描述 珠玑妙算游戏(the game of master mind)的玩法如下: 计算机有4个槽,每个槽放一个球,颜色可能是红色(R)、黄色…...

【rust语言】rust多态实现方式
文章目录 前言一、多态二、rust实现多态trait的静态方式还有一种方式可以通过动态分发,还以上面那段代码,比如dyn关键字 泛型方式枚举方式优点:缺点: 总结 前言 学习rust当中遇到了这个问题,记录一下,不对…...

两年半机场,告诉我如何飞翔
为说明如何坐飞机离港,故此记录一篇。何为离港,顾名思义,离开港湾,那何为港湾,便是机场。 机场,一个你可能经常去,亦或不曾去之地。我想,管你去没去过,先说下怎么去&…...
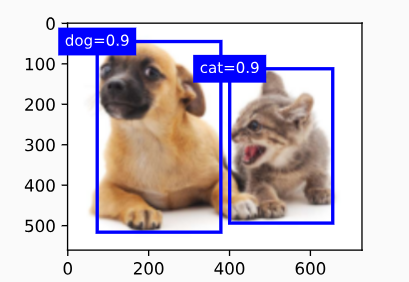
【动手学深度学习】--21.锚框
锚框 学习视频:锚框【动手学深度学习v2】 官方笔记:锚框 1.锚框 目标检测算法通常会在输入图像中采样大量的区域,然后判断这些区域中是否包含我们感兴趣的目标,并调整区域边界从而更准确地预测目标的真实边界框(gro…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
