线性代数的学习和整理7:各种特殊效果矩阵汇总
目录
1 矩阵
1.1 1维的矩阵
1.2 2维的矩阵
1.3 没有3维的矩阵---3维的是3阶张量
1.4 下面本文总结的都是各种特殊效果矩阵特例
2 方阵: 正方形矩阵
3 单位矩阵
3.1 单位矩阵的定义
3.2 单位矩阵的特性
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
3.4 零矩阵
3.4 看下这个矩阵 [0,1;1,0]
3.5 看下这个矩阵 [1,1;1,1]
4 镜像矩阵
5 旋转矩阵
5.1 定义
5.2 以下是选择矩阵的原理(转载)
5.3 旋转矩阵应用转移点: 旋转矩阵右乘其他矩阵才可以
6 伸缩矩阵
7 剪切矩阵
8 平移矩阵???
待补充:其他特殊矩阵
1 矩阵
1.1 1维的矩阵
- 行向量,αT
- 列向量,α
行向量
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
\end{matrix}
\right]
$$
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
\end{matrix}
\right]
$$
列向量
$$
\left[
\begin{matrix}
1 \\
4 \\
7
\end{matrix}
\right]
$$
1.2 2维的矩阵
- 一般2维表都可以看作矩阵。
- 矩阵的每个维度可以是1个数字,也可以是多个数字组成的数组/向量
- 比如 An*m就是n 行 m列的矩阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{matrix}
\right] \tag{1}
$$
1.3 没有3维的矩阵---3维的是3阶张量
- 比如3个坐标轴
1.4 下面本文总结的都是各种特殊效果矩阵特例
- 单位矩阵
- 零矩阵
- 等等
2 方阵: 正方形矩阵
- 行数和列数相等的矩阵即方阵
- 比如 An*n就是n 行 n列的矩阵
- 方阵有很多特殊的属性
- 比如虽然并不是,方阵一定有逆矩阵,但是可逆矩阵必须是方阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix}
\right]
$$
3 单位矩阵
3.1 单位矩阵的定义
- 单位矩阵,一定是这样的[1,0;0,1]
- 单位矩阵的作用,矩阵A*I=A
- 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射,不做任何改变
- 也就是单位矩阵,既不改变矩阵方向,也不改变伸缩矩阵的长短,完全不变
$$
\left[
\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
$$

3.2 单位矩阵的特性
- 单位矩阵的特性
- A*I=A
- A*A-=I
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
- 因为 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射,不做任何改变
- 而[1,1;1,1] 没有啥意义
- 可比较下面的结果,实际理解

3.4 零矩阵
- [0,0;0,0]
- 所有的列向量,都坍缩回原点
$$
\left[
\begin{matrix}
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
$$

3.4 看下这个矩阵 [0,1;1,0]
- [0,1;1,0]
- 这个矩阵,和单位矩阵形式恰好相反
- 从几何效果来看,是镜像矩阵(列向量互换了)
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$

3.5 看下这个矩阵 [1,1;1,1]
- [1,1;1,1]
- 几何效果是,矩阵的列向量会被变成完全相等(方向,长度都相等)
$$
\left[
\begin{matrix}
1 & 1 \\
1 & 1 \\
\end{matrix}
\right]
$$

4 镜像矩阵
- [0,1;1,0]
- 这个矩阵,和单位矩阵形式恰好相反
- 从几何效果来看,是镜像矩阵(列向量互换了)
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$

5 旋转矩阵
5.1 定义
- 经典的旋转矩阵及其变形
- cos(θ) -sin(θ)
sin(θ) cos(θ) - 可以实现,逆时针旋转效果
$$
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
$$
$$
\left[
\begin{matrix}
1 & 0 & 0 \\
0 & cos(θ) & -sin(θ) \\
0 & sin(θ) & cos(θ) \\
\end{matrix}
\right]
$$
5.2 以下是选择矩阵的原理(转载)
旋转变换(一)旋转矩阵_csxiaoshui的博客-CSDN博客本文主要介绍了计算机图形学中的旋转的概念和矩阵的描述方式,包括二维和三维旋转矩阵的推导过程_旋转矩阵https://blog.csdn.net/csxiaoshui/article/details/65446125

5.3 旋转矩阵应用转移点: 旋转矩阵右乘其他矩阵才可以
- 旋转矩阵的重点:旋转矩阵A*x 就是必须旋转矩阵右乘其他矩阵才能旋转,反之不行!
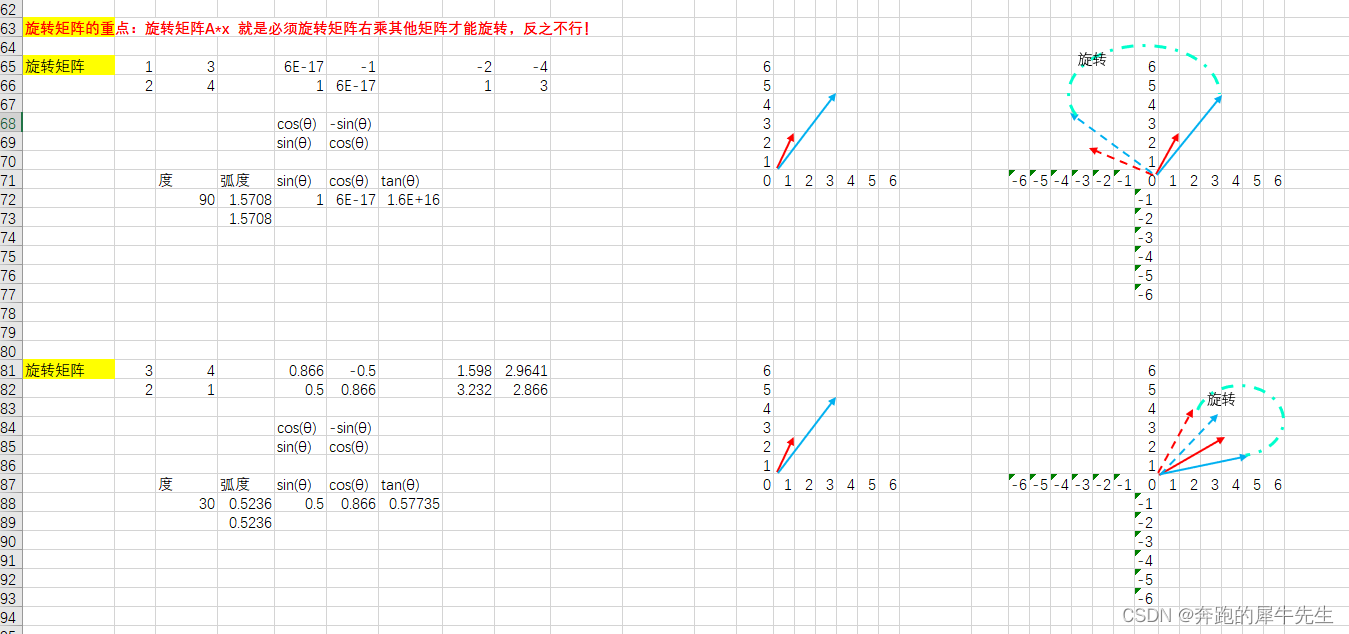
6 伸缩矩阵
放大缩小倍数矩阵
- 把[1,0;0,1] 变成[2,0;0,1],即可实现伸缩效果
- 比如变成[2,0;0,1],是第1个列向量变长2倍
- 比如变成[1,0;0,-2],是第2个列向量变长2倍,且方向要相反(向原点的另外一边)
- 正负号实现,同方向,或反方向
- 数值大小>1实现放大效果,反之<1是缩小效果

$$
\left[
\begin{matrix}
2 & 0 \\
0 & 1 \\
\end{matrix}
\right]
$$

7 剪切矩阵
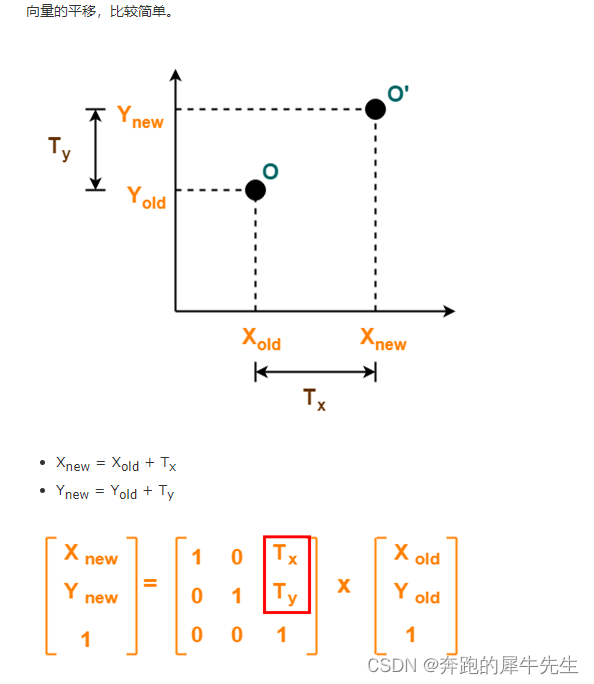
8 平移矩阵???
https://www.cnblogs.com/meteoric_cry/p/7987548.html![]() https://www.cnblogs.com/meteoric_cry/p/7987548.html
https://www.cnblogs.com/meteoric_cry/p/7987548.html
待补充:其他特殊矩阵
相关文章:

线性代数的学习和整理7:各种特殊效果矩阵汇总
目录 1 矩阵 1.1 1维的矩阵 1.2 2维的矩阵 1.3 没有3维的矩阵---3维的是3阶张量 1.4 下面本文总结的都是各种特殊效果矩阵特例 2 方阵: 正方形矩阵 3 单位矩阵 3.1 单位矩阵的定义 3.2 单位矩阵的特性 3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]…...

[git]github上传大文件
github客户端最高支持100Mb文件上传,如果要>100M只能用git-lfs,但是测试发现即使用git lfs,我上传2.5GB也不行,测试737M文件可以,GitHub 目前 Git LFS的总存储量为1G左右,超过需要付费。(上传失败时&…...

element ui - el-select获取点击项的整个对象item
1.背景 在使用 el-select 的时候,经常会通过 change 事件来获取当前绑定的 value ,即对象中默认的某个 value 值。但在某些特殊情况下,如果想要获取的是点击项的整个对象 item,该怎么做呢? 2.实例 elementUI 中是可…...

实现SSM简易商城项目的购物车实现
实现SSM简易商城项目的购物车实现 在这篇博客中,我们将使用SSM框架来实现一个简易的购物车功能。我们将使用Spring框架来管理Bean,使用SpringMVC框架来处理HTTP请求,使用MyBatis框架来操作数据库。 实现SSM简易商城项目的购物车功能的思路如…...
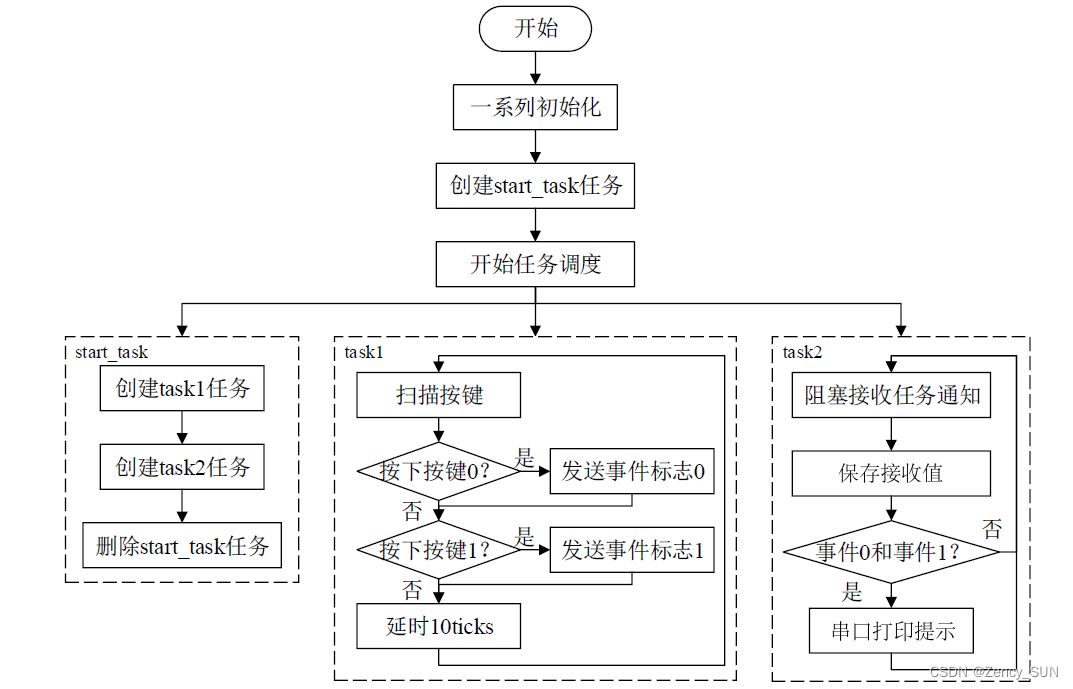
【学习FreeRTOS】第17章——FreeRTOS任务通知
1.任务通知的简介 任务通知:用来通知任务的,任务控制块中的结构体成员变量 ulNotifiedValue就是这个通知值。 使用队列、信号量、事件标志组时都需另外创建一个结构体,通过中间的结构体进行间接通信! 使用任务通知时,…...
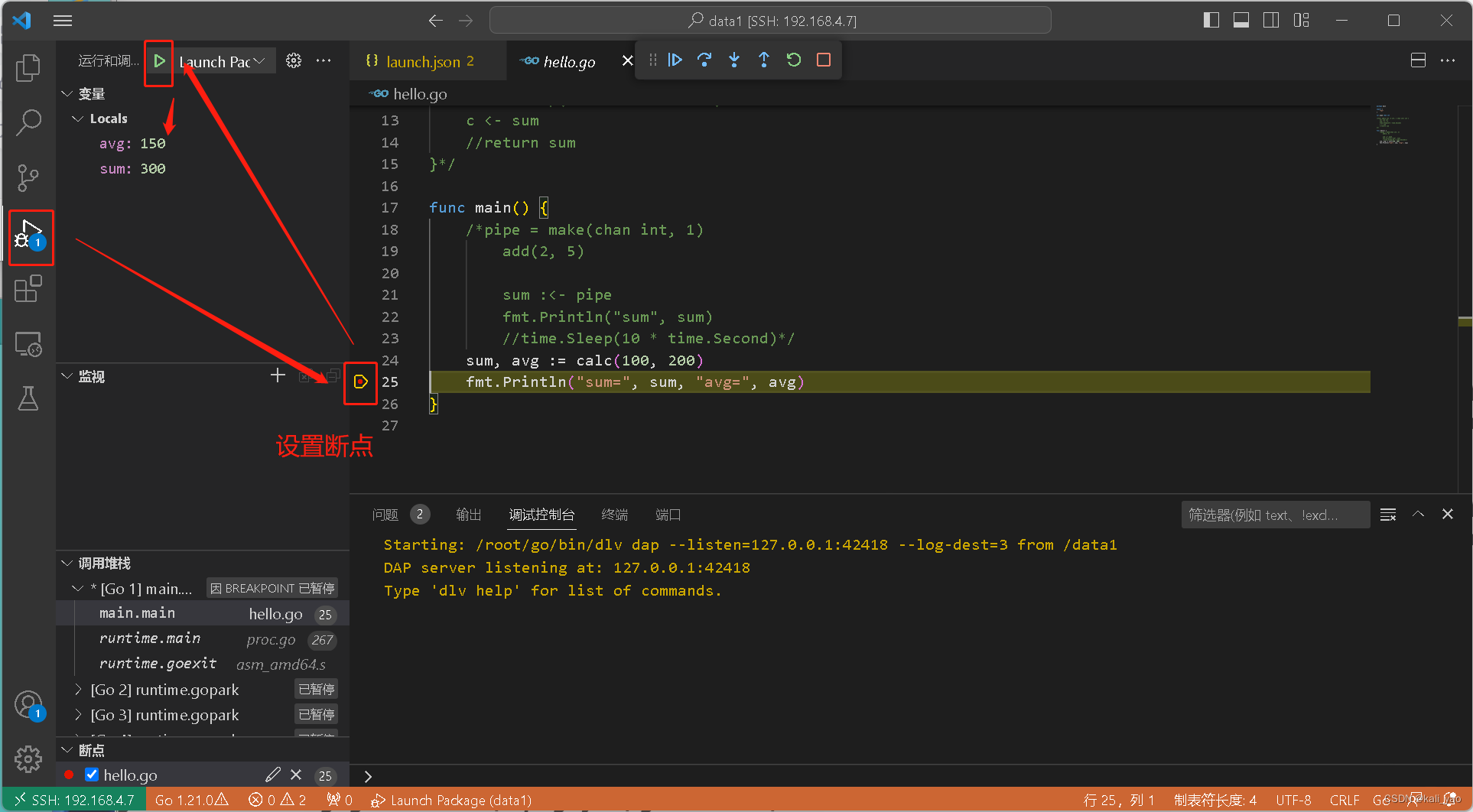
GO-vscode远程开发和调试
本文内容主要包括: 概述: 主要就是把代码放到服务器上然后远程去开发和调试 工具: vscode 远程端: linux 一.安装远程插件 vscode安装Remote - SSH,Remote Explorer,Remote Development,…...

【笔记】判断两个Double类型的值是否相同
在Java中,将两个double值转换为String类型,然后使用equals方法进行比较是一个常见的做法,但是这种方法并不是完全可靠,特别是在涉及浮点数的精度时仍然可能会遇到问题。 浮点数在内部以二进制表示,有时会存在舍入误差…...
Linux —— nfs文件系统
简介 NFS 是Network File System的缩写,即网络文件系统。一种使用于分散式文件系统的协定,由Sun公司开发,于1984年向外公布。功能是通过网络让不同的机器、不同的操作系统能够彼此分享个别的数据,让应用程序在客户端通过网络访问位…...
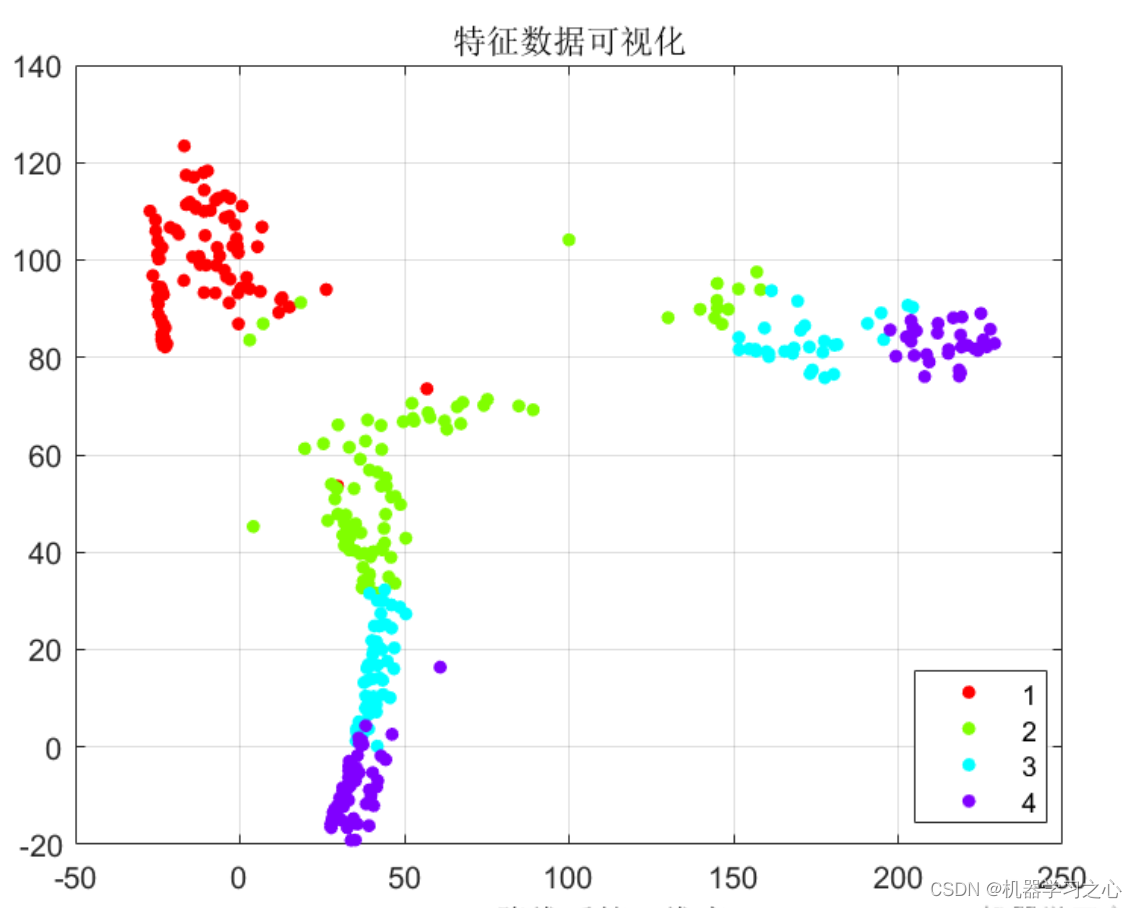
数据降维 | MATLAB实现T-SNE降维特征可视化
数据降维 | MATLAB实现T-SNE降维特征可视化 目录 数据降维 | MATLAB实现T-SNE降维特征可视化降维效果基本描述程序设计参考资料 降维效果 基本描述 T-SNE降维特征可视化,MATLAB程序。 T-分布随机邻域嵌入,主要用途是对高维数据进行降维并进行可视化&…...
)
蓝桥杯上岸每日N题 (交换瓶子)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 题目描述 有 N 个瓶子,编号 1∼N,放在架子上。 比如有 5 个瓶子: 2 1 3 5 4 要求每次拿起 2 个瓶子,交换它们的位置。 …...
GMS基本模块TIN、Solids、Modflow2000/2005、MT3DMS、MODPATH。及其在地下水流动、溶质运移、粒子追踪方面的应用
解决地下水数值模拟技术实施过程中遇到的困难,从而提出切实可行的环境保护措施,达到有效保护环境、防治地下水污染,推动经济社会可持续发展的目的。 (1)水文地质学,地下水数值模拟基础理论;&am…...
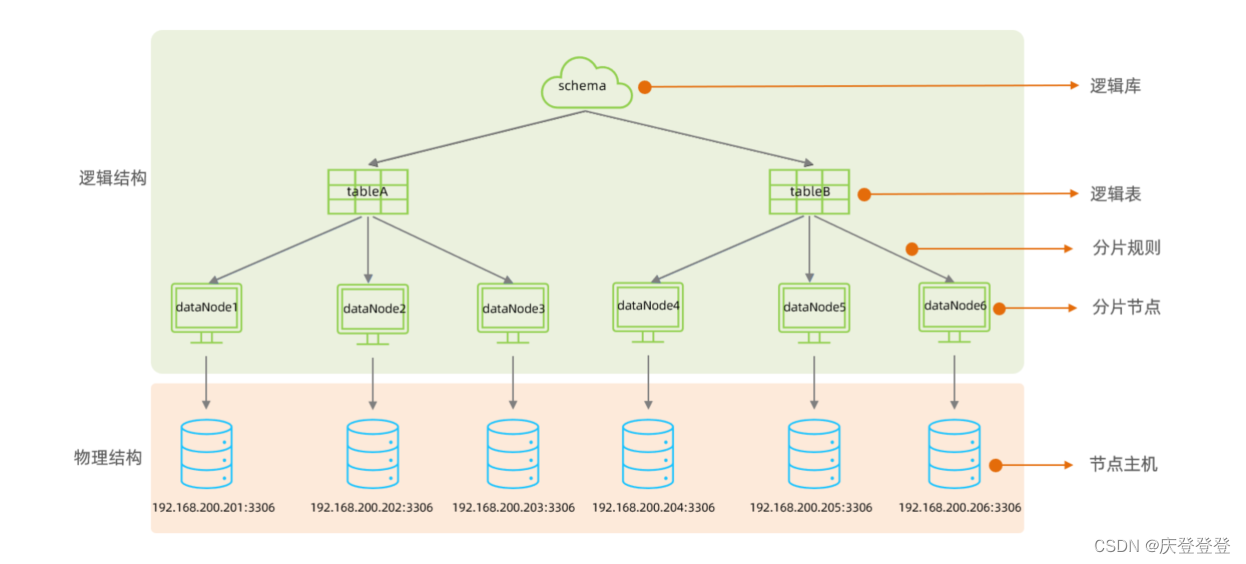
MySQL数据库中间件Mycat介绍及下载安装(教程)
一,介绍 MyCat是开源的、活跃的、基于Java语言编写的MySQL数据库中间件。可以像使用MySQL一样来使用MyCat,对于开发人员来说根本感觉不到MyCat的存在。 开发人员只需要连接MyCat即可,而具体底层用到几台数据库,每一台数据库服务器…...
【VMware】CentOS 设置静态IP(Windows 宿主机)
文章目录 1. 更改网络适配器设置2. 配置虚拟网络编辑器3. 修改 CentOS 网络配置文件4. ping 测试结果 宿主机:Win11 22H2 虚拟机:CentOS-Stream-9-20230612.0 (Minimal) 1. 更改网络适配器设置 Win R:control 打开控制面板 依次点击&#x…...
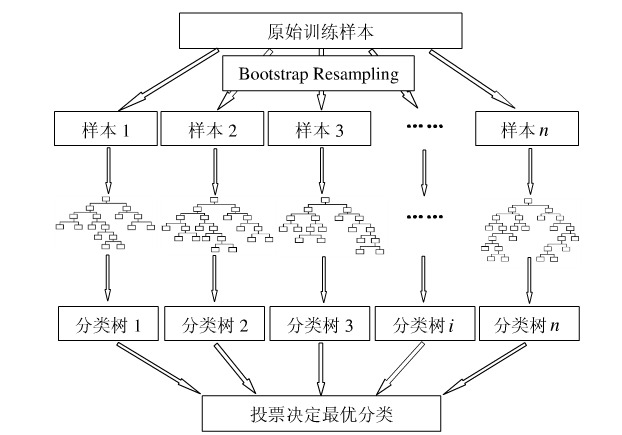
机器学习十大算法之七——随机森林
0 引言 集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据上构建多个横型,集成所有模型的建模结果,基本上所有的机器学习领域都可以看到集成学习…...
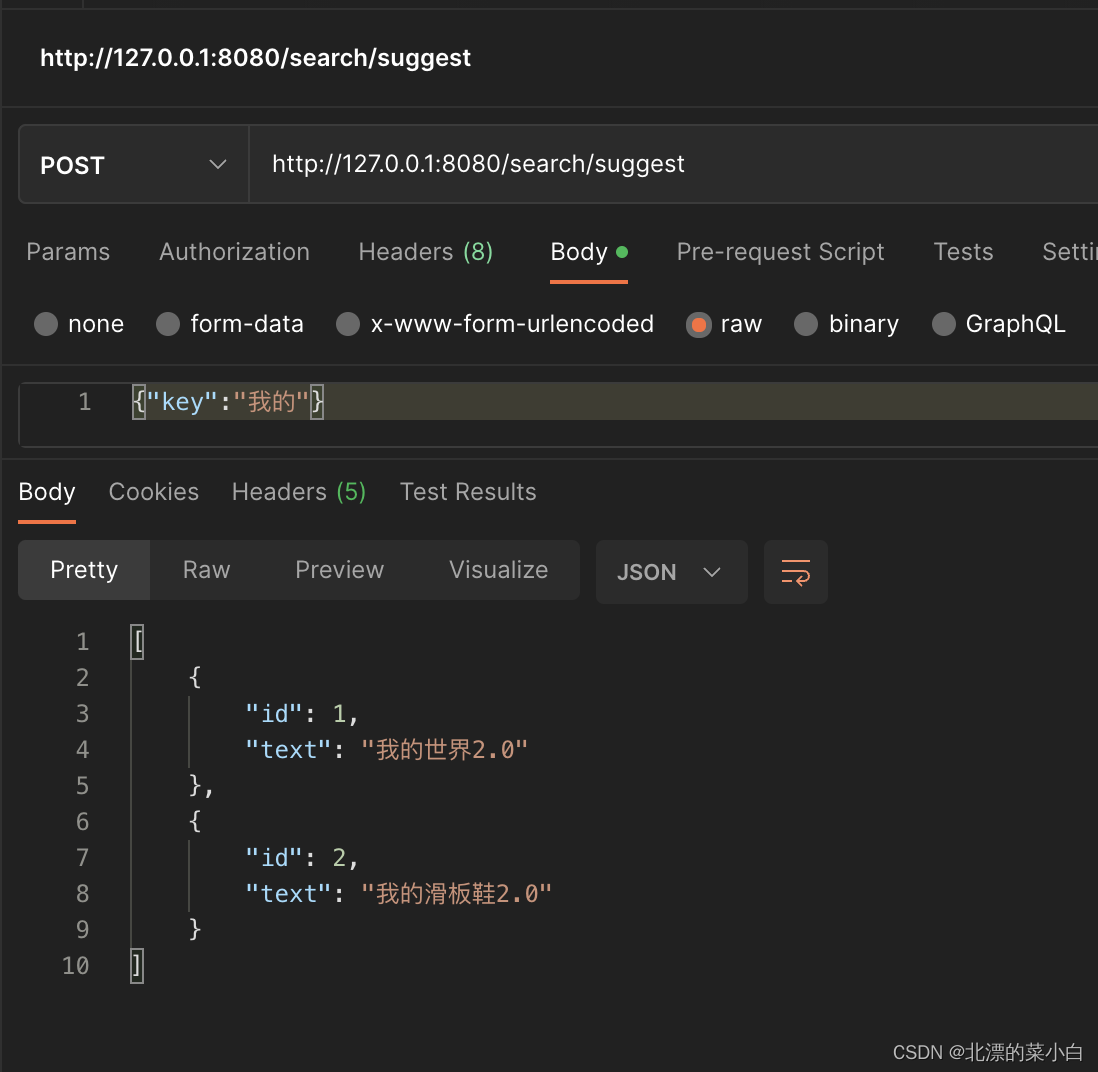
spring boot 3使用 elasticsearch 提供搜索建议
业务场景 用户输入内容,快速返回建议,示例效果如下 技术选型 spring boot 3elasticsearch server 7.17.4spring data elasticsearch 5.0.1elasticsearch-java-api 8.5.3 pom.xml <dependency><groupId>org.springframework.boot</gr…...

住宅IP:解锁更快速、稳定的互联网,你准备好了吗?
随着互联网的广泛普及,我们对网络的需求也越来越高。无论是工作、学习还是娱乐,我们都希望能够享受到更快速、稳定的互联网连接。而在实现这一目标的过程中,住宅IP正逐渐崭露头角,成为了一种备受关注的解决方案。那么,…...

支持dolby vision的盒子接支持dolby vision的电视,在adaptive hdr时,播放非dv的hdr视频,输出sdr
支持dolby vision的盒子接支持dolby vision的电视,setting选择adaptive hdr,按照这个配置在播放非dv的hdr视频时,会输出sdr。 看起来是很不合理的,高级的产品播放高级的片源,却输出低级的画质。 想要搞清楚这个问题&am…...
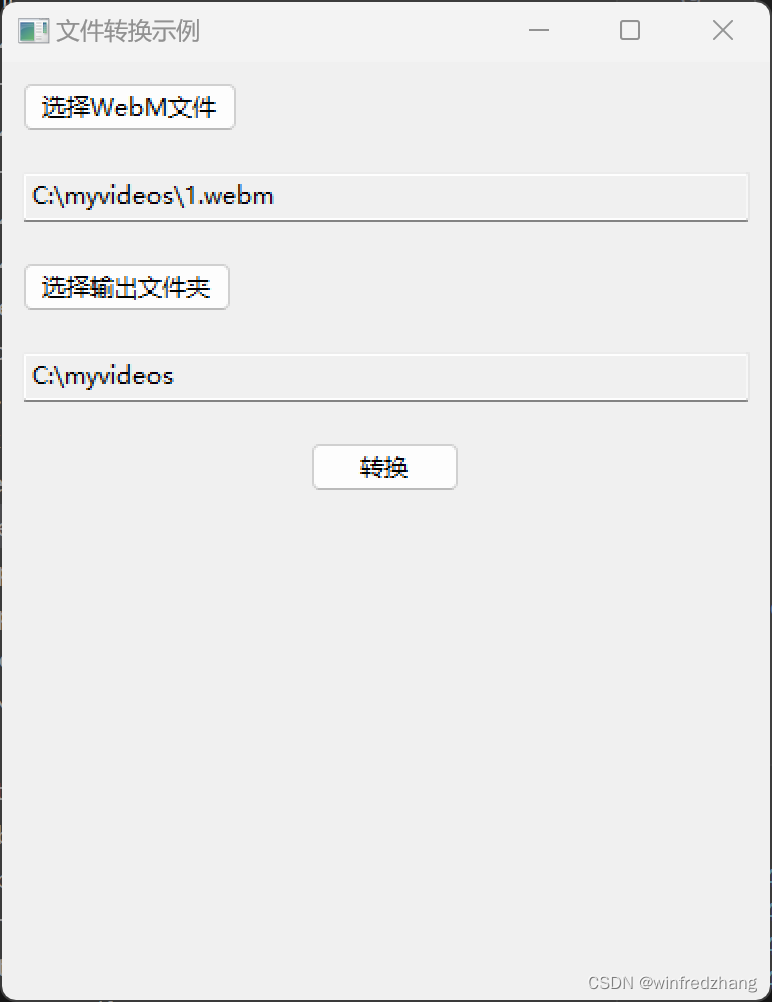
使用ffmpeg将WebM文件转换为MP4文件的简单应用程序
tiktok网上下载的short视频是webm格式的,有些程序无法处理该程序,比如roop程序,本文介绍了如何使用wxPython库创建一个简单的GUI应用程序,用于将WebM文件转换为MP4文件。这个应用程序使用Python编写,通过调用FFmpeg命令…...

Prompt-“设计提示模板:用更少数据实现预训练模型的卓越表现,助力Few-Shot和Zero-Shot任务”
Prompt任务(Prompt Tasks) 通过设计提示(prompt)模板,实现使用更少量的数据在预训练模型(Pretrained Model)上得到更好的效果,多用于:Few-Shot,Zero-Shot 等…...

玩转Mysql系列 - 第6篇:select查询基础篇
这是Mysql系列第6篇。 环境:mysql5.7.25,cmd命令中进行演示。 DQL(Data QueryLanguage):数据查询语言,通俗点讲就是从数据库获取数据的,按照DQL的语法给数据库发送一条指令,数据库将按需求返回数据。 DQ…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
