动态规划入门:斐波那契数列模型以及多状态(C++)
斐波那契数列模型以及多状态
- 动态规划简述
- 斐波那契数列模型
- 1.第 N 个泰波那契数(简单)
- 2.三步问题(简单)
- 3.使⽤最⼩花费爬楼梯(简单)
- 4.解码方法(中等)
- 简单多状态
- 1.打家劫舍(中等)
- 2.打家劫舍II(中等)
- 3.粉刷房子(中等)
- 4.删除并获得点数(中等)
- 5.买卖股票的最佳时期含⼿续费(中等)
- 6.买卖股票的最佳时机含冷冻期(中等)
- 7.买卖股票的最佳时机III(困难)
- 8.买卖股票的最佳时机IV(困难)
动态规划简述
动态规划(Dynamic programming,简称 DP)是一种解决多阶段决策问题的算法思想。它将问题分解为多个阶段,并通过保存中间结果来避免重复计算,从而提高效率。
动态规划的解题步骤一般分为以下几步:
- 思考状态表示,创建dp表(重点)
- 分析出状态转移方程(重点)
- 初始化
- 确定填表顺序
- 确定返回值
斐波那契数列模型
1.第 N 个泰波那契数(简单)
链接:第 N 个泰波那契数
- 题目描述

- 做题步骤
- 状态表示
面对动态规划问题,我们一般有两种状态表示:
- 以某一个位置为起点,……
- 以某一个位置为终点,……
我们一般优先考虑第1种表示,但如果第1种无法解决就考虑第2种。

-
状态转移方程
这个题目直接告诉了我们状态转移方程:dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] -
初始化
泰波那契数的第0、1、2个是特殊的,不满足状态转移方程,因此我们需要初始化这三个位置为0、1、1 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序很明显是从左往右 -
返回值
根据状态表示,假设要求的是第n个,返回的应该是dp[n]
- 代码实现
class Solution {
public:int tribonacci(int n) {//对于第0、1、2单独处理if(n == 0) return 0;if(n == 1 || n == 2)return 1;//dp[i]:第i个泰波那契数vector<int> dp(n + 1);dp[0] = 0; dp[1] = 1; dp[2] = 1; for(int i = 3; i < n + 1; i++){dp[i] = dp[i-1] + dp[i-2] + dp[i-3];}return dp[n];//空间复杂度:O(N)//时间复杂度:O(N)}
};//不知道大家有没有发现向后填表的过程其实只需要前置的3个状态
//其余的状态都是多余的,我们可以用有限的变量来保存这些状态,这样就实现了空间优化
//这种优化方式被称为“滚动数组”
//经过优化原O(N)->O(1) O(N^2)->O(N)
//但这并不是动态规划讲解的要点,所以我只会把两种优化情况的代码给出// class Solution {
// public:
// int tribonacci(int n)
// {
// if(n == 0)
// return 0;
// if(n == 1 || n == 2)
// return 1;// int t1 = 0;
// int t2 = 1;
// int t3 = 1;
// int ret = 0;// for(int i = 3; i < n + 1; i++)
// {
// ret = t1 + t2 + t3;
// t1 = t2;
// t2 = t3;
// t3 = ret;
// }
// return ret;
// }
// };
2.三步问题(简单)
链接:三步问题
-
题目描述

-
做题步骤
-
状态表示
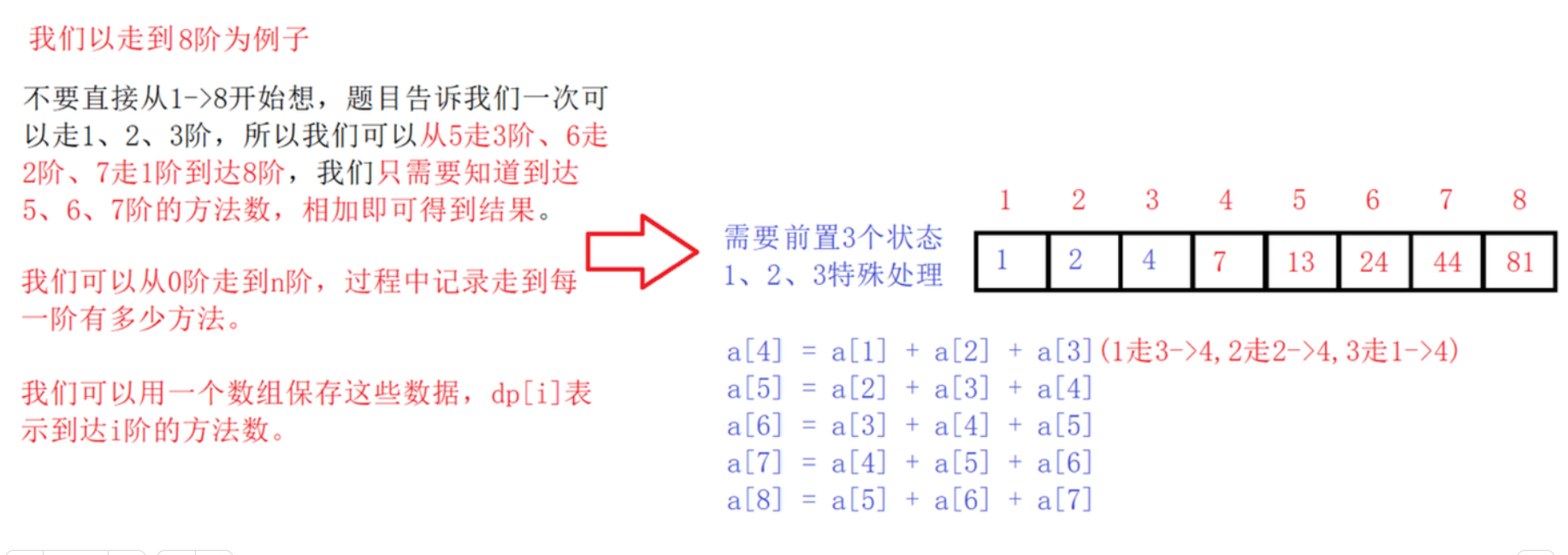
-
状态转移方程
到达i阶可以转换成先到达i - 3、i - 2、i - 1阶,三者相加得到结果,所以状态转移方程为:dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]。 -
初始化
为了保证填表不越界,我们把到达1、2、3阶的方法初始化。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序从左往右。 -
返回值
根据状态表示,假设要求的是n阶,返回的应该是dp[n]
- 代码实现
class Solution {
public:int waysToStep(int n) {//1、2、3阶特殊处理if(n == 1) return 1;if(n == 2) return 2;if(n == 3) return 4;//dp[i]表示到达i阶的方法数vector<int> dp(n+1); //多开一个空间,可以让下标和层数对应dp[1] = 1; dp[2] = 2; dp[3] = 4;const int mod = 1e9 + 7; //有可能超出,需要取模for(int i = 4; i < n + 1; i++){dp[i] = ((dp[i-1] + dp[i-2]) % mod + dp[i-3]) % mod;}return dp[n];//时间复杂度:O(N)//空间复杂度:O(N)}
};
3.使⽤最⼩花费爬楼梯(简单)
链接:使⽤最⼩花费爬楼梯
-
题目描述

-
做题步骤
-
状态表示
这个题目的思路和第2题很相似,要到达终点n阶,我们可以从n - 1阶走一步、n - 2阶走两步到终点,从中选择费用最低的一方(从当前阶离开需要支付离开费用);至于到达n - 1、n - 2阶的最低费用,我们可以以n - 1、n - 2层为终点进行分析,依此类推。到达终点的过程需要到达每一层的最低费用,我们可以用一个dp表存储,dp[i]表示到达下标i台阶所需要的最低费用。 -
状态转移方程
到达i阶的最低花费可以转换为min(到达i - 1阶的最低花费 + 走出这一阶的花费, 到达i - 2阶的最低花费 + 走出这一阶的花费),所以状态转移方程为:dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])。 -
初始化
由转移方程可知更新某个状态需要前置的两个状态,为了确保填表时不越界,单独处理走到0、1阶的最低花费。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序从左往右。 -
返回值
根据状态表示,假设数组有n个元素(终点是n阶),返回的应该是dp[n]
- 代码实现
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) { //dp[i] 表示到这一层的最小花费int n = cost.size();vector<int> dp(n + 1);//一开始就可以在0或1阶,花费为0,vector默认给0,不用处理for(int i = 2; i < n + 1; i++){dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);}return dp[n];//空间复杂度:O(N)//时间复杂度:O(N)}
};// //第二种写法:反着来,以某个位置为起点,……
// class Solution {
// public:
// int minCostClimbingStairs(vector<int>& cost)
// {
// //dp[i]:这一层为起点,到终点的最低花费
// int n = cost.size();
// vector<int> dp(n + 1);
// dp[n] = 0;
// dp[n - 1] = cost[n - 1];
// for(int i = n - 2; i >= 0; i--)
// {
// dp[i] = min(dp[i + 1] + cost[i], dp[i + 2] + cost[i]);
// }// return min(dp[0], dp[1]);
// }
// };
4.解码方法(中等)
链接:解码方法
-
题目描述

-
做题步骤
-
状态表示
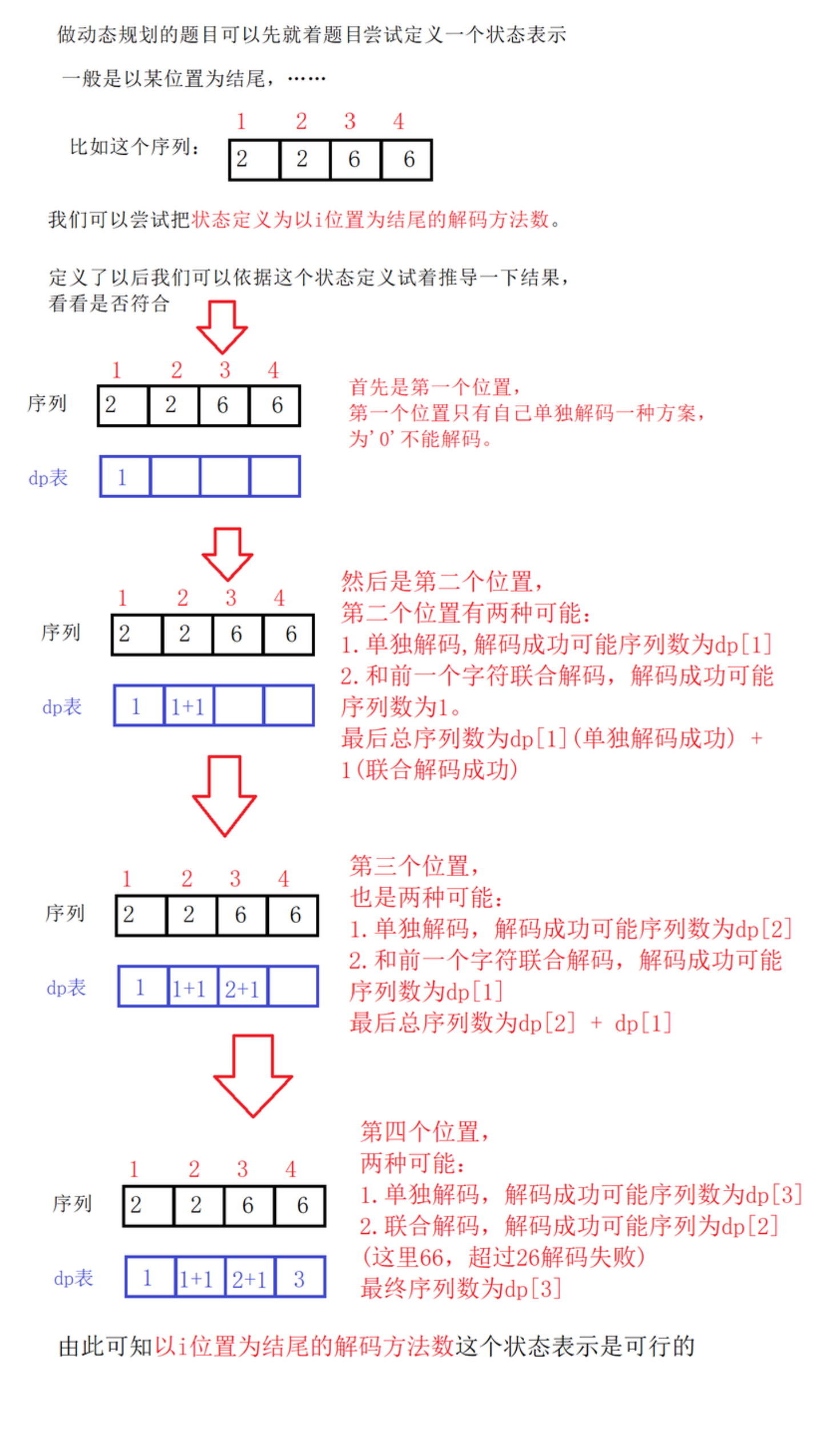
-
状态表示
除去第一位,每个位置都有单独解码和联合解码两种方式,n位置的状态转移方程为:dp[n] = dp[n - 1](单独解码成功)+ dp[n - 2](联合解码成功) -
初始化
依据状态转移方程,某位置状态需要前置的两个状态,为了避免越界,我们需要单独处理第1、2个位置,但观察上面的分析过程,可以发现第2个位置和其它位置一样也有两种解码可能,我们可以在dp表前面多加个虚拟节点并初始为1,这样就只需要处理第1个位置了。(看图看图)
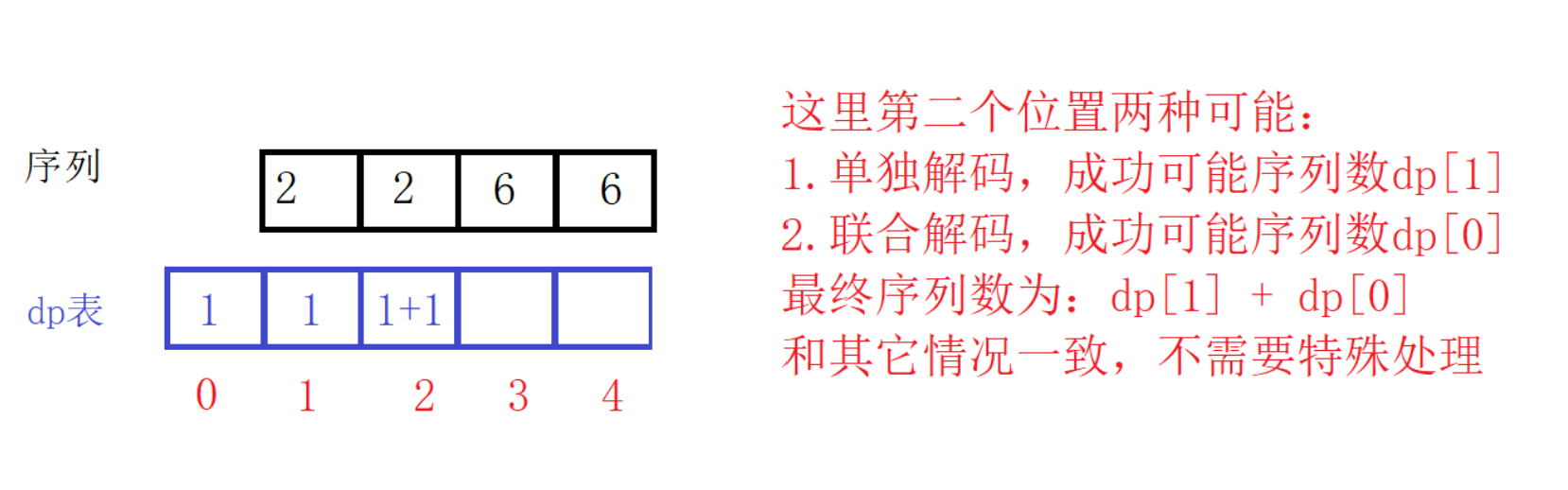
-
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序从左往右。 -
返回值
依据状态定义,假设序列长度为n,返回的应该是以n位置为结尾的解码可能数,即dp[n]。
- 代码实现
class Solution {
public:int numDecodings(string s) {int n = s.size();//dp[i]表示以i位置为结尾的解码可能数vector<int> dp(n + 1);//第一个位置就为0,最终结果已经是0if(s[0] == '0')return 0;//初始化虚拟节点和第1个位置dp[1] = dp[0] = 1;for(int i = 2; i < n + 1; i++){//单独解码if(s[i - 1] != '0') dp[i] += dp[i-1];//联合解码(联合解码小于10说明存在前导0,无法联合解码)int com = (s[i - 2] - '0') * 10 + (s[i - 1] - '0');if(com >= 10 && com <= 26) dp[i] += dp[i-2];//都失败的情况是'00',最终结果已经是0,这里可不加//两个连续的0,后面全都是0if(dp[i] == 0)return 0; }return dp[n];}
};
简单多状态
1.打家劫舍(中等)
链接:打家劫舍
-
题目描述

-
做题步骤
- 状态表示
依据前面的做题经验,我们可以把状态表示为以i位置为结尾的最大偷窃金额,但每个位置有偷和不偷两种选择,所以可以把状态再进行细化:状态f表示以i位置为结尾并偷窃本位置的最大金额;状态g表示以i位置为结尾但不偷窃本位置的最大金额。
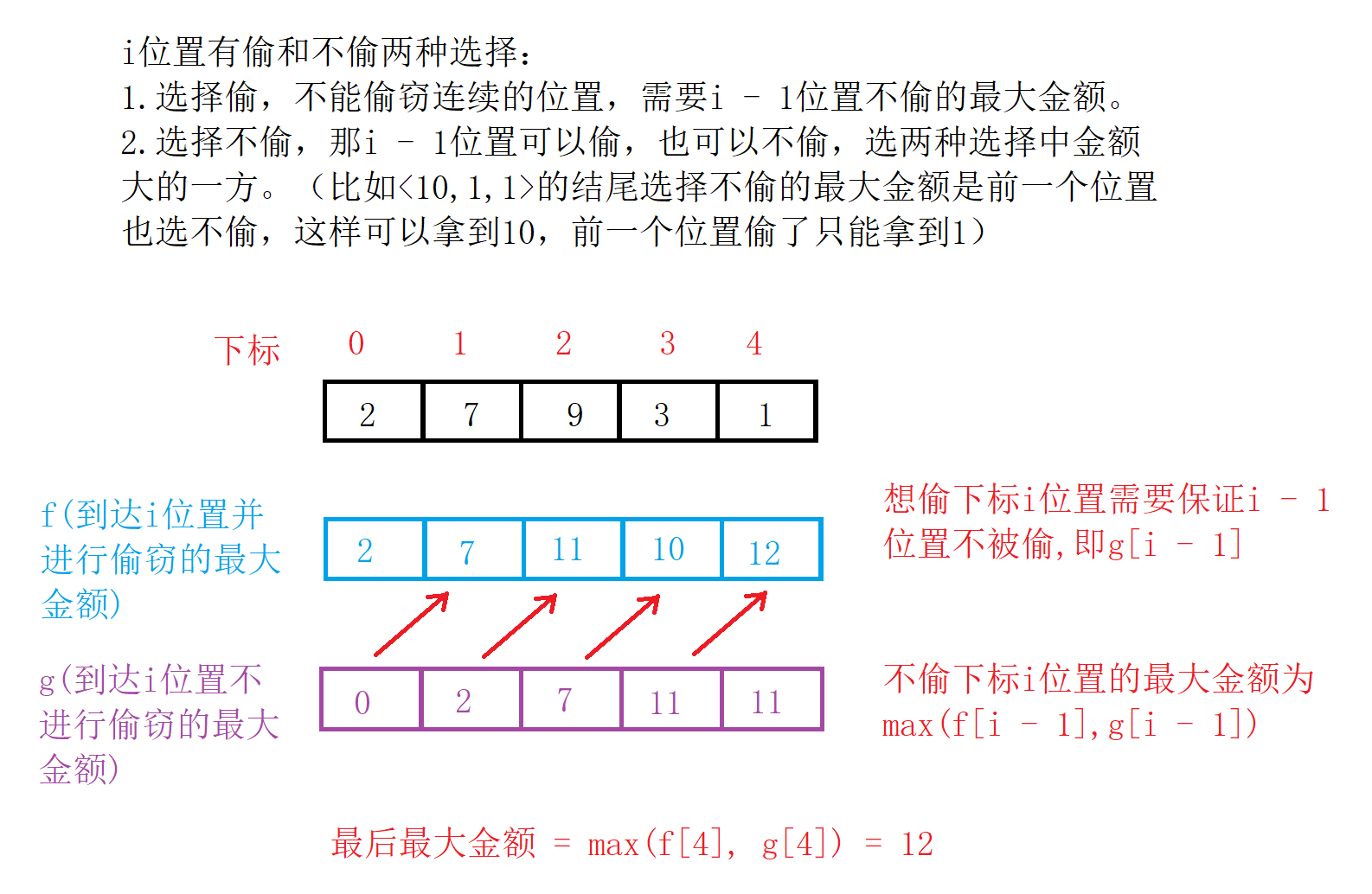
-
状态转移方程
由前面的分析可知,要偷i位置(f)需要i - 1位置不偷(g)的最大金额,不偷i位置就选择i - 1位置偷和不偷两种选择中大的一方,所以状态转移方程为:
(1) f[i] = g[i - 1] + nums[ i ] (本位置可偷金额);
(2) g[i] = max(g[i - 1], f[i - 1]) -
初始化
由状态转移方程可知当今状态需要前一个状态,为保证填表时不越界,单独处理第一个位置:f[0] = nums[0],g[0] = 0。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序从左往右。 -
返回值
把自己代入成小偷,相邻位置不能同时偷的情况下是需要进行选择的,但偷的过程中不知道后面房子的价值,只能走一步看一步,保证每一步都是最好的,偷到最后一定是最优结果。假设数组有n个元素,返回值为max(f[n - 1], g[n - 1])。
- 代码实现
class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();vector<int> f(n); //f[i]表示到底这个位置并偷窃的最大金额auto g = f; //g[i]表示到达这个位置不偷窃的最大金额f[0] = nums[0]; //初始化f[0],g[0]默认0不用处理for(int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(g[i - 1], f[i - 1]);}return max(f[n - 1], g[n - 1]);//空间复杂度:O(N)//时间复杂度:O(N)}
};
2.打家劫舍II(中等)
链接:打家劫舍II
-
题目描述

-
做题步骤
-
状态表示
这个题和前一个题唯一的不同只有首尾成环这一个点,我们延用上个题目的状态表示:状态f表示以i位置为结尾并偷窃本位置的最大金额;状态g表示以i位置为结尾但不偷窃本位置的最大金额。
处理成环问题,最直接的思路就是拆解。
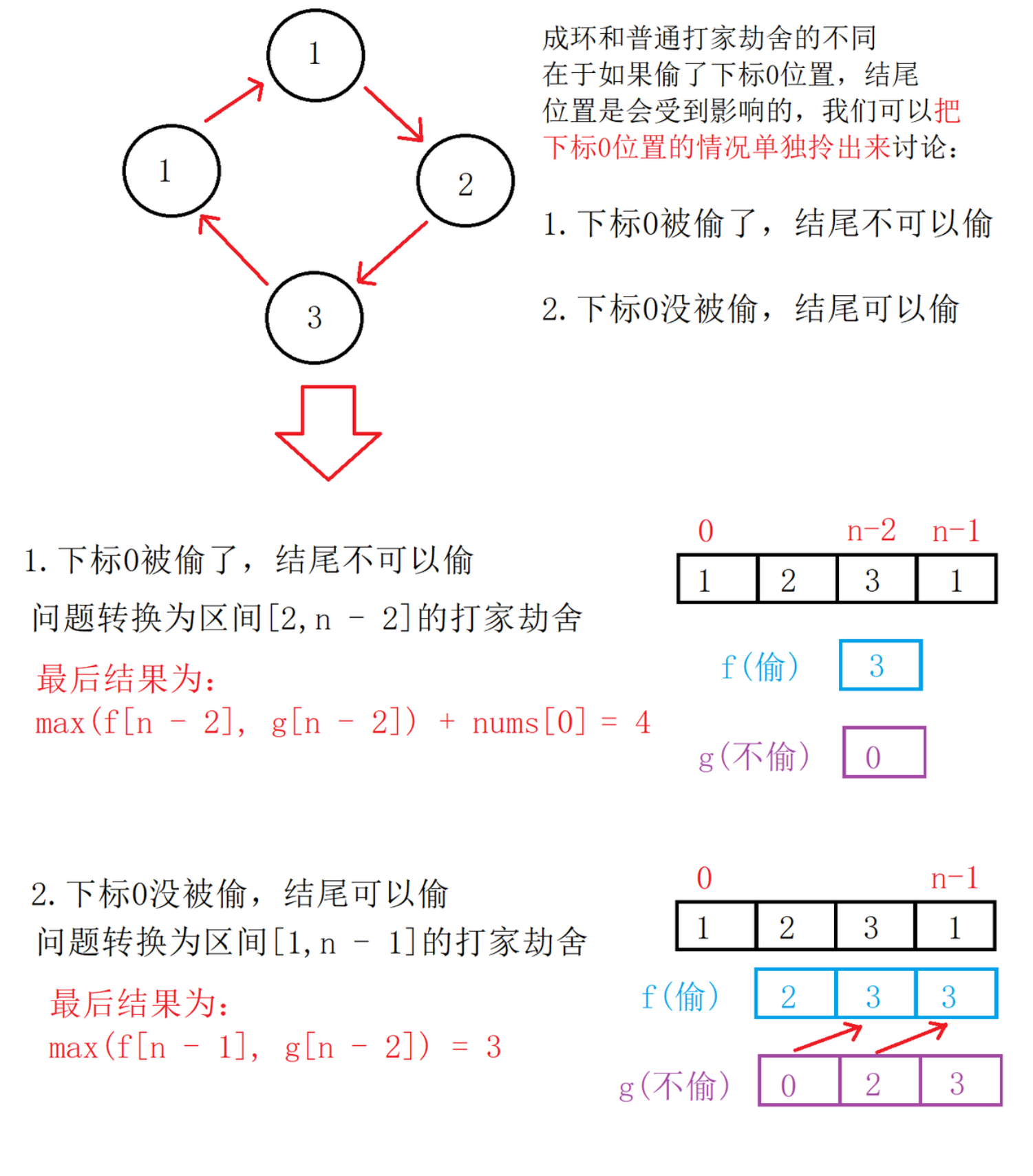
-
状态转移方程
和上一道题目一致,状态转移方程为:
(1) f[i] = g[i - 1] + nums[ i ] (本位置可偷金额);
(2) g[i] = max(g[i - 1], f[i - 1]) -
初始化
和上一道题目一致。 -
填表顺序
从左往右。 -
返回值
_rob函数表示指定区间的打家劫舍,返回值为:
max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1))。
- 代码实现
class Solution {
public:int _rob(vector<int>& nums, int left,int right) {//区间不存在返回0if(left > right)return 0;int n = nums.size();vector<int> f(n); //到这个屋子偷的最大金额auto g = f; //到这个屋子不偷的最大金额f[left] = nums[left];for(int i = left + 1; i <= right; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1],g[i - 1]);}return max(f[right],g[right]);}int rob(vector<int>& nums) {int n = nums.size();return max(nums[0] + _rob(nums, 2, n - 2), _rob(nums, 1, n - 1));}
};
3.粉刷房子(中等)
链接:粉刷房子
-
题目描述

-
做题步骤
-
状态表示
依据经验和题目要求,我们可以把状态定义为把第i号房子粉刷成j颜色的最小花费。
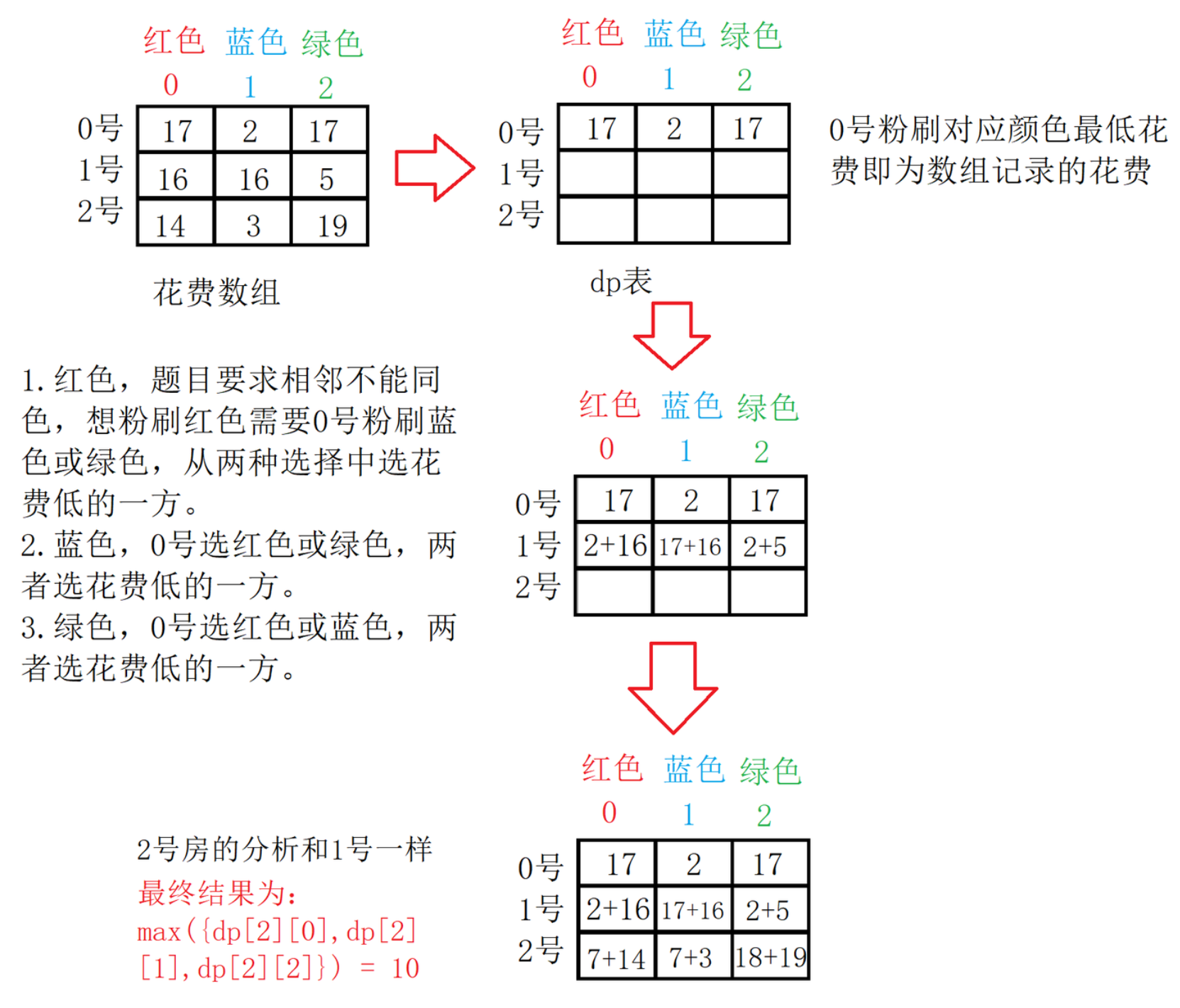
-
状态转移方程
状态转移方程为(0是红色、1是蓝色、2是绿色):
(1)dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + cost[i][0](花费)
(2)dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + cost[i][1]
(3)dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + cost[i][2] -
初始化
为了保证填表不越界,我们要初始化第一行的值,但是那样太麻烦了,我们可以多开一行并初始化0,这样就不用单独处理第一行了。(注意和cost数组的下标对应关系) -
填表顺序
从上往下,每一行从左往右。
5.返回值
依据状态表示,假设最后的房子是i号,返回值为min({dp[n][0], dp[n][1], dp[n][2]})。
- 代码实现
class Solution {
public:int minCost(vector<vector<int>>& costs){int n = costs.size();//dp[i][j]表示第i号房子粉刷成j颜色的最低花费//其中0表示红色,1表示蓝色,2表示绿色vector<vector<int>> dp(n + 1, vector<int>(3));//空间多开一行并初始化0,不用单独处理第一行for (int i = 1; i < n + 1; i++){dp[i][0] = costs[i - 1][0] + min(dp[i - 1][1], dp[i - 1][2]);dp[i][1] = costs[i - 1][1] + min(dp[i - 1][0], dp[i - 1][2]);dp[i][2] = costs[i - 1][2] + min(dp[i - 1][0], dp[i - 1][1]);}return min({dp[n][0], dp[n][1], dp[n][2]});//时间复杂度:O(N)//空间复杂度:O(N)}
};
4.删除并获得点数(中等)
链接:删除并获得点数
-
题目描述

-
做题步骤
-
状态表示
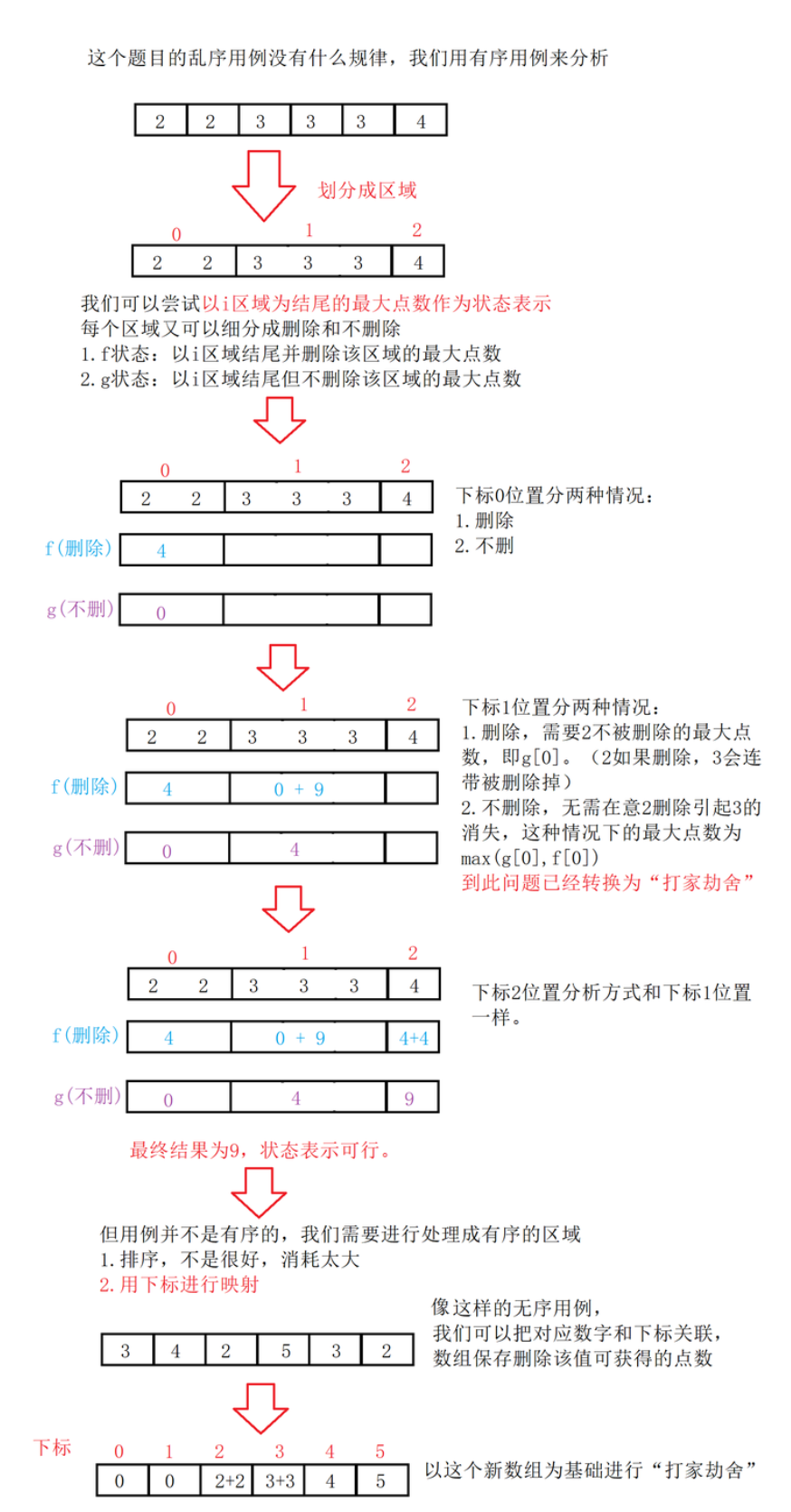
-
状态转移方程
这个题就是变形的“打家劫舍”,转移方程一致:
(1) f[i] = g[i - 1] + v[ i ] (删除本位置可得点数);
(2) g[i] = max(g[i - 1], f[i - 1]) -
初始化
数组转化完成后dp表不需要处理。 -
填表顺序
从左往右。 -
返回值
返回值为max(f[N - 1],g[N - 1])
- 代码实现
class Solution {
public:int deleteAndEarn(vector<int>& nums){int n = nums.size();//创建数组进行映射//题目中1 <= nums[i] <= 10000const int N = 10001;int v[N] = {0};for(auto val : nums)v[val] += val;//“打家劫舍”vector<int> f(N); //f[i]表示以i区域为结尾并且删除本区域的最大点数auto g = f; //g[i]表示以i区域为结尾但不删除本区域的最大点数for (int i = 1; i < N; i++){f[i] = g[i - 1] + v[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[N - 1],g[N - 1]);//时间复杂度:O(N)//空间复杂度:O(1)}
};//上面的写法简洁一些,但无论数据量多少都会遍历10000次
//可以记录数组的最大、最小值,来加快速度
// class Solution {
// public:
// int deleteAndEarn(vector<int>& nums)
// {
// int n = nums.size();
// vector<int> v(10001);
// //先遍历一次
// int _max = nums[0];
// int _min = nums[0];
// for (int i = 0; i < n; i++)
// {
// v[nums[i]] += nums[i];
// _max = max(_max, nums[i]);
// _min = min(_min, nums[i]);
// }// vector<int> f(10001);
// auto g = f;
// for (int i = _min; i <= _max; i++)
// {
// f[i] = g[i - 1] + v[i];
// g[i] = max(f[i - 1], g[i - 1]);
// }// return max(f[_max],g[_max]);
// }
// };
5.买卖股票的最佳时期含⼿续费(中等)
链接:买卖股票的最佳时期含⼿续费
-
题目描述

-
做题步骤
- 状态表示
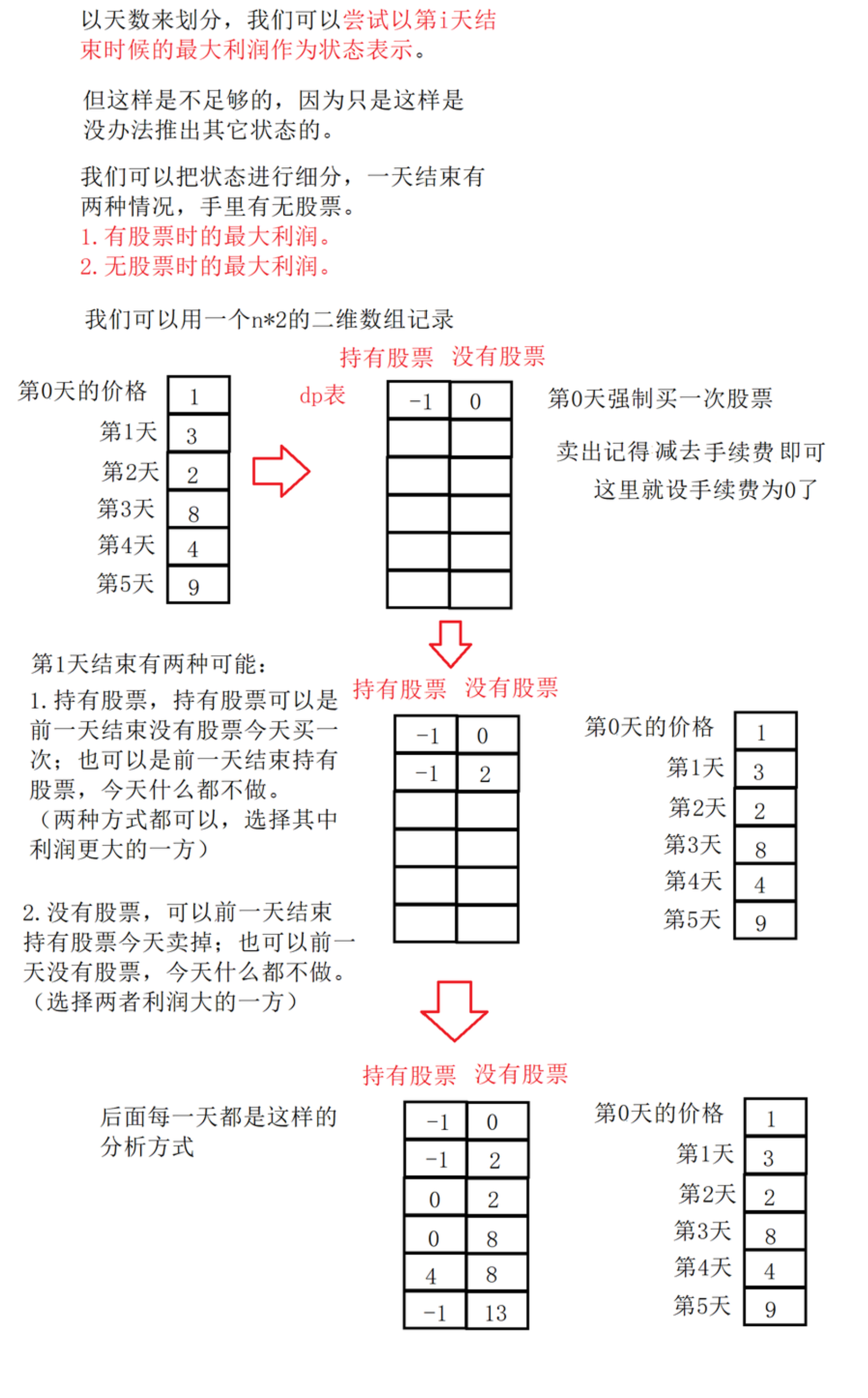
dp[i][j]:第i天结束时处于j状态的最大利润。
-
状态转移方程,0表示结束有股票,1表示结束没有股票,fee是手续费,prices[i]表示第i天的股票价格
(1)dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
(2)dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee) -
初始化
初始化第0天状态即可,dp[0][0] -= prices[0];。 -
填表顺序
从上到下。 -
返回值
返回值为:max(dp[n - 1][1], dp[n - 1][0])。
- 代码实现
class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();//dp[i][j]:第i天结束处于j状态的最大利润vector<vector<int>> dp(n, vector<int>(2));//这种解法买入还是卖出交手续费都一样(反正买入了一定会卖出)dp[0][0] -= prices[0];for(int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);}return max(dp[n - 1][1], dp[n - 1][0]);//时间复杂度:O(N)//空间复杂度:O(N)}
};
6.买卖股票的最佳时机含冷冻期(中等)
链接:买卖股票的最佳时机含冷冻期
-
题目描述

-
做题步骤
-
状态表示

-
状态转移方程
0是买入(有股票)、1是可交易、2是冷冻,prices[i]表示第i天的股票价格,状态转移方程为:
(1)dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0])
(2)dp[i][1] = max(dp[i - 1][2], dp[i - 1][1])
(3)dp[i][2] = dp[i - 1][0] + prices[i] -
初始化
当前天的三种状态需要前一天的状态,所以初始化dp表的第一行
dp[0][0]:想该天结束后处于买入状态,必须把股票买了,dp[0][0] = -prices[i];
dp[0][1]:什么都不干,dp[0][1] = 0;
dp[0][2]:想该天结束处于冷冻,在同一天买入和卖出,dp[0][2] = 0; -
填表顺序
从上到下。 -
返回值
最大值应该手中没有股票,假设数组有n个元素,最大值为max(dp[n - 1][1], dp[n - 1][ 2 ])。
- 代码实现
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();//dp[i][j]:第i天结束后处于j状态时的最大利润vector<vector<int>> dp(n, vector<int>(3));//初始化dp[0][0] -= prices[0];for(int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][1] - prices[i], dp[i - 1][0]);dp[i][1] = max(dp[i - 1][2], dp[i - 1][1]);dp[i][2] = dp[i - 1][0] + prices[i];}return max(dp[n - 1][2],dp[n - 1][1]);}
};
7.买卖股票的最佳时机III(困难)
链接:买卖股票的最佳时机III
-
题目描述

-
做题步骤
-
状态表示

-
状态转移方程
由前面的分析可知,状态转移方程为:
(1)f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i])
(2)if(j >= 1) g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i])
else g[i][j] = g[i - 1][j] -
初始化
需要i = 0的状态,初始化第一行。
(1)处于第一行的时候只有f[0][0]和g[0][0]存在,f[0][0] = -prices[0],g[0][0] = 0。
(2)为了避免不存在的状态干扰取max值,我们把不存在的状态统一初始化为 INT_MIN / 2。(INT_MIN会越界,尽可能小就行) -
填表顺序
从上往下填每一列,从左往右填每一行。 -
返回值
返回最后一行的最大值即可。
- 代码实现
class Solution {
public://可能会越界,取INT_MIN的一半const int INF = INT_MIN / 2;int maxProfit(vector<int>& prices) {int n = prices.size();//dp[i][j]表示在第i天结束后完成j次交易,处于""状态下的最大利润vector<vector<int>> f(n, vector<int>(3, INF)); //买入auto g = f; //可交易//初始化f[0][0] = -prices[0];g[0][0] = 0;for (int i = 1; i < n; i++){for(int j = 0; j < 3; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];//j == 0的时候前置状态f[i - 1][j - 1]不存在if(j >= 1)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);} }return max({g[n - 1][0], g[n - 1][1], g[n - 1][2]});}
};
8.买卖股票的最佳时机IV(困难)
这个题目的思考方式和第7题完全一致,大家可以先自己试着做一下。
链接:买卖股票的最佳时机IV
- 代码实现
class Solution {
public:const int INF = INT_MIN / 2;int maxProfit(int k, vector<int>& prices) { int n = prices.size();//n天最多完成n / 2次交易,k不能超过这个值k = min(k, n / 2);//买入//dp[i][j]表示在第i天结束后完成j次交易,处于""状态下的最大利润vector<vector<int>> f(n, vector<int>(k + 1, INF));//卖出auto g = f;//初始化(先买再说)f[0][0] = -prices[0];g[0][0] = 0;for (int i = 1; i < n; i++){for(int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j >= 1)g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);} }int ret = g[n - 1][0];//把利润最大的那个找出来for(int j = 1; j <= k; j++){ret = max(ret, g[n - 1][j]);}return ret;}
};
相关文章:

动态规划入门:斐波那契数列模型以及多状态(C++)
斐波那契数列模型以及多状态 动态规划简述斐波那契数列模型1.第 N 个泰波那契数(简单)2.三步问题(简单)3.使⽤最⼩花费爬楼梯(简单)4.解码方法(中等) 简单多状态1.打家劫舍ÿ…...

LeetCode438.找到字符串中所有字母异位词
因为之前写过一道找字母异位词分组的题,所以这道题做起来还是比较得心应手。我像做之前那道字母异位词分组一样,先把模板p排序,然后拿滑动窗口去s中从头到尾滑动,窗口中的这段字串也给他排序,然后拿这两个排完序的stri…...

【微服务】03-HttpClientFactory与gRpc
文章目录 1.HttpClientFactory :管理外向请求的最佳实践1.1 核心能力1.2 核心对象1.3 HttpClient创建模式 2.gRPC:内部服务间通讯利器2.1 什么是gRPC2.2 特点gRPC特点2.3.NET生态对gRPC的支持情况2.4 服务端核心包2.5 客户端核心包2.5 .proto文件2.6 gRP…...
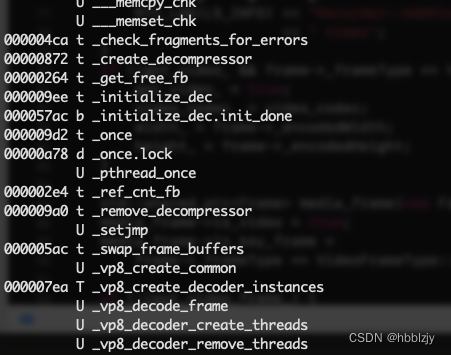
iOS开发之查看静态库(.a/.framework)中包含的.o文件和函数符号(ar,nm命令)
.a/.framework其实是把编译生成的.o文件,打包成一个.a/.framework文件。a的意思是archive/归档的意思。 查看静态库.a文件包含的内容用下面的命令解压: ar x xxx.a 用ar命令打包静态库: 参数r是将后面的*.o或者*.a文件添加到目标文件中 参数…...

Idea常用快捷键--让你代码效率提升一倍(一)
一、代码编辑相关快捷键 1.单行复制(实现快速创建多个对象)CtrlD 2.空出下一行 ShiftEnter 3.单行注释快捷键 ctrl / 4.快速构建构造函数,setter,getter、toString方法 AltInsert 4.显示快速修复和操作的菜单 altenter 5.格式化代码:C…...

【Open3D】第二篇:GUI编程
文章目录 基本控件创建创建文本框创建button创建布局 绘制形状绘制线段绘制点云 设置属性设置线宽设置点大小 可用Shader汇总GUI框架 基本控件创建 创建文本框 push_edit gui.TextEdit()创建button push_button gui.Button(...) push_button.horizontal_padding_em 0.5 p…...

【Python】P0 本系列博文简介与大纲
Python 前言本系列博文适合谁本系列博文不适合谁本系列博文大纲 前言 本系列博文基于《Python Cookbook》一书,Python 3 版本;本系列博文的目标不是为了构建一个 Python 知识大全,而是为了那些需要快速将 Python 学以致用的相关人员…...
FL Studio 21.1.0 Build 3713中文破解免费下载安装激活
FL Studio 21是一个功能齐全、开放式的PC音乐创作和制作环境。它具有基于音乐序列器的图形用户界面。 这个数字音频工作站将您所需的一切整合在一个包中,用于创作、编排、录制、编辑、混音和掌握专业质量的音乐。 FL Studio 21是从你的大脑到扬声器的最快方式。制作…...

从0开始配置eslint
没有在.eslintrc文件中配置parserOptions指定语言版本和模块类型 {"parserOptions": {"ecmaVersion": 7, //指定es版本为es2016"sourceType": "module", //使用import导入模块} }eslint还不能识别jsx语法 {"parserOptions"…...

Activity 的启动流程(Android 13)
Activity 的启动过程分为两种:一种是普通 Activity 的启动过程,另一种是根 Activity 的启动过程。普通 Activity 指的是除应用程序启动的第一个 Activity 之外的其他 Activity。根 Activity 指的是应用程序启动的第一个 Activity,因此&#x…...

deepspeed学习资料
记录一些deepspeed学习过程中的好文章 【进行中】1、DeepSpeed使用指南(简略版)_Reza.的博客-CSDN博客 - 含deepspeed的安装方法 - 含 zero config的不同配置,stage1、stage2、stage3的配置和解释...

数据分享|R语言PCA主成分、lasso、岭回归降维分析近年来各国土地面积变化影响...
全文链接:http://tecdat.cn/?p31445 机器学习在环境监测领域的应用,着眼于探索全球范围内的环境演化规律,人类与自然生态之间的关系以及环境变化对人类生存的影响(点击文末“阅读原文”获取完整代码数据)。 课题着眼于…...

Docker-Consul
Docker-Consul 一、介绍1.什么是服务注册与发现2.什么是consul3.consul提供的一些关键特性: 二、consul 部署1.环境准备2.consul服务器3.查看集群信息4.通过 http api 获取集群信息 三、registrator服务器1.安装 Gliderlabs/Registrator2.测试服务发现功能是否正常3…...
display模块)
Pygame编程(2)display模块
pygame编程2-display设备显示 pygame.display.init() 初始化 display 模块init() -> None pygame.display.get_init() 获取display初始化 状态,如果已经初始化,返回 True,否则返回Falseget_init() -> bool pygame.display.quit() 退出…...

第十五天|104.二叉树的最大深度、111.二叉树的最小深度、 222.完全二叉树的节点个数
104.二叉树的最大深度 题目链接:104. 二叉树的最大深度 - 力扣(LeetCode) /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullp…...

图像识别技术在医疗领域的革命:探索医学影像诊断的未来
导言: 随着人工智能和计算机视觉的快速发展,图像识别技术在医疗领域正掀起一场革命。医学影像诊断是医疗工作中的重要环节,而图像识别技术的引入为医生提供了更准确、高效的辅助手段。本文将深入探讨图像识别技术在医疗领域的应用,…...
计网第四章(网络层)(二)
目录 IPV4地址编址 第一历史阶段(分类编址): A类地址: B类地址: C类地址: D类地址(多播地址): E类地址(保留地址): 第二历史阶…...

原生微信小程序使用 wxs;微信小程序使用 vant-weapp组件
1.原生微信小程序使用 wxs 1.内嵌 WXS 脚本 2. 定义外链 wxs 3. 使用外连wxs 在这里插入图片描述 2. 微信小程序使用 vant weapp 1.安装步骤 2. 安装包管理(package.json)文件的方法 操作顺序 :文档地址 如果使用 typescript 需要操作步骤3,否则不…...
qml相关知识1
qml相关知识1 QtQuick.Controls 哪个版本支持TreeModel 和 TreeItemqt5.12开始,TreeItem 类被删除,无法使用delegate 什么时候可以用Qt5.15中没有 import QtQuick.Controls 1吗,哪个版本有control1qml如何两种版本的controls混用(…...

linux+c+qt杂记
虚拟机网络选择; 桥接模式:设置window宿主机的IP/dns,把虚拟机设置为桥接即可。 切换到终端:我的是 ctrlaltFnF1? 问题解决: Ubuntu系统下载(清华大学开源软件镜像站)(ubuntu-20.…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
