Codeforces Round 894 (Div. 3)
还是打一下卡!!!
(A,B,C)
目录
A. Gift Carpet
链接 :
题面 :
题目意思 :
思路 :
代码 :
B. Sequence Game
链接 :
题面 :
编辑
题目意思 :
思路 :
代码 :
C. Flower City Fence
原题链接 :
题面 :
题目意思 :
思路 :
代码 :
A. Gift Carpet
链接 :
Problem - A - Codeforces
题面 :

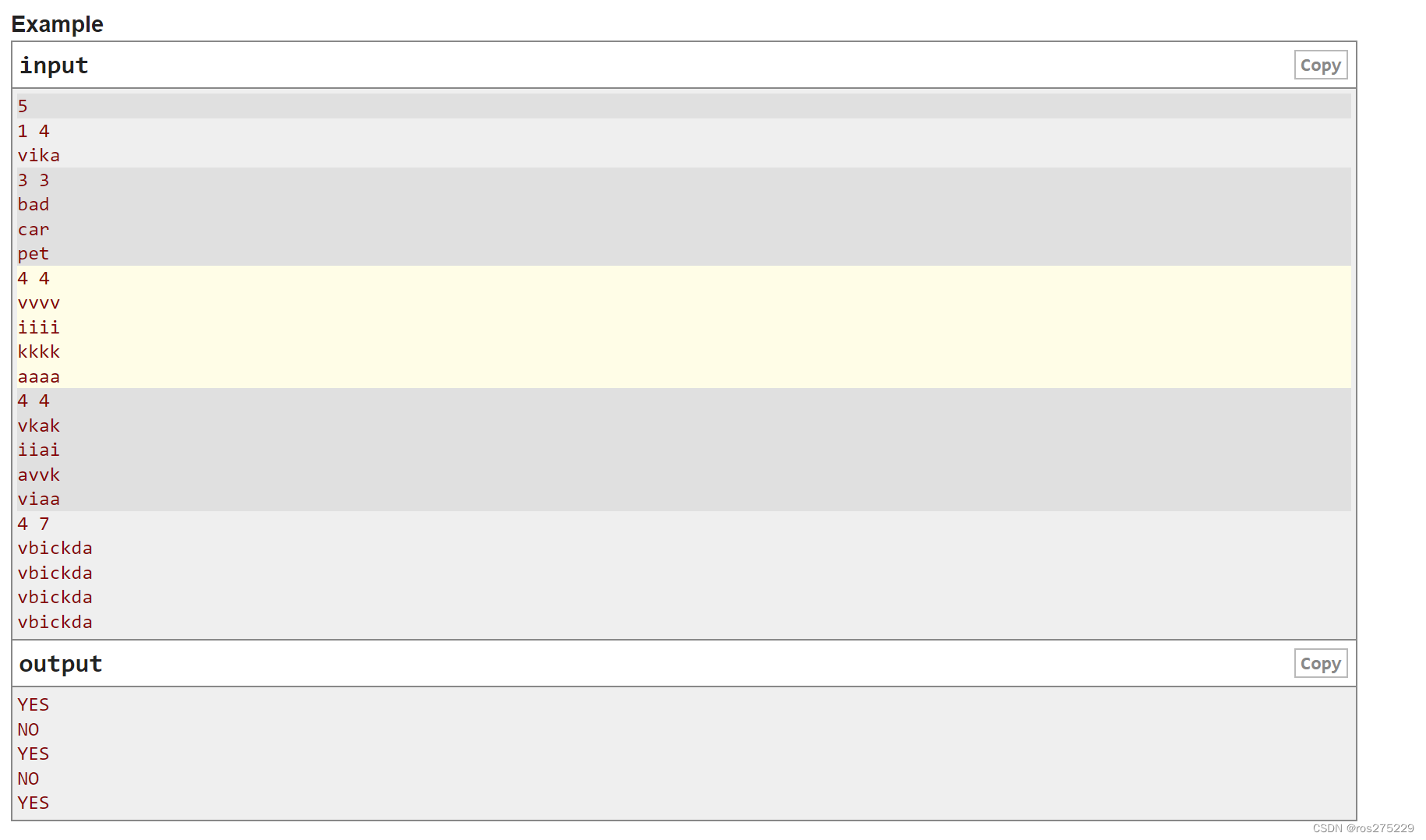
题目意思 :
最近,Tema和Vika庆祝了家庭日。他们的朋友Arina送给他们一块地毯,可以表示为一个n×m的小写拉丁字母表格。
Vika还没看到礼物,但是Tema知道她喜欢什么样的地毯。如果她能够在上面读到她的名字,她就会喜欢这块地毯。她按照从左到右、逐列阅读的方式,每列选择一个或零个字母。
具体来说,如果可以按照从左到右的顺序选择四列不同的列,使得第一列包含"v",第二列包含"i",第三列包含"k",第四列包含"a",那么这个女孩就会喜欢这块地毯。
帮助Tema提前了解Vika是否会喜欢Arina的礼物。
思路 :
就是一个暴力的遍历整个矩阵,然后运用贪心的思想,最好在前面能找到的字母就将其标出来,然后记录找到vika的出现字母次数的变量t加一,最后返回t==4;
代码 :
// A
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 21;
int n,m,t;
char a[N][N];inline void solve(){cin>>n>>m;for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j];if(m<4){ cout<<"NO"<<endl; return ; }t = 0;for(int j=1;j<=m;j++){for(int i=1;i<=n;i++){if(t==0){if(a[i][j] == 'v'){ t++; break;}}else if(t==1){if(a[i][j] == 'i'){ t++; break;}}else if(t==2){if(a[i][j] == 'k'){ t++; break;}}else if(t==3){if(a[i][j] == 'a'){ t++; break;}} }if(t==4) break; }if(t==4) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}int main()
{IOSint _;cin >> _;// _ = 1; while(_ --) solve();return 0;
}B. Sequence Game
链接 :
Problem - B - Codeforces
题面 :
题目意思 :
Tema和Vika正在玩以下游戏。
首先,Vika想出一个长度为m的正整数序列a,并将其写在一张纸上。然后她拿一张新纸,按照以下规则写下序列b:
首先,她写下a1。 然后,她只写下那些满足ai-1≤ai的ai(2≤i≤m)。将这个序列的长度表示为n。 例如,从序列a=[4,3,2,6,3,3],Vika将得到序列b=[4,6,3]。
然后她将带有序列b的纸递给Tema。他尝试猜出序列a。
Tema认为在这样的游戏中赢得胜利非常不可能,但还是希望找到至少一个可能由Vika最初选择的序列a。帮助他输出任何这样的序列。
请注意,输出序列的长度不应超过输入序列长度的两倍。
思路 :
数组构造题 :
例如给定[4,6,3]要在a[i-1]和a[i]两数中间加或不加一个数x满足a[i-1]>x && x <=a[i],那么怎么构造呢?
1.如果a[i]>=a[i-1]的话,就不用插入x了,已经满足同时取a[i-1]和a[i]了;
2.否则 : 也就是要插入一个数了,一定要看清题目:构造数组中元素的值>=1,所以a[i]=1的情况下,x取比a[i]小的数的话,就会造成插入数为0或负数的可能,那么就只剩下插a[i]了,这样符合题意;
下面请看代码 :
代码 :
// B
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5+10;
int n,a[N],mi;
vector<int> v;inline void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];v.clear();v.push_back(a[1]);for(int i=2;i<=n;i++){if(a[i] >= a[i-1]) v.push_back(a[i]);else {v.push_back(a[i]);v.push_back(a[i]);}}cout<<v.size()<<endl;for(int num : v) cout<<num<<" ";cout<<endl;
}int main()
{IOSint _;cin >> _;// _ = 1; while(_ --) solve();return 0;
}C. Flower City Fence
个人认为这是一道比较有意思的题目(数学模拟题),hhh;
原题链接 :
Problem - C - Codeforces
题面 :

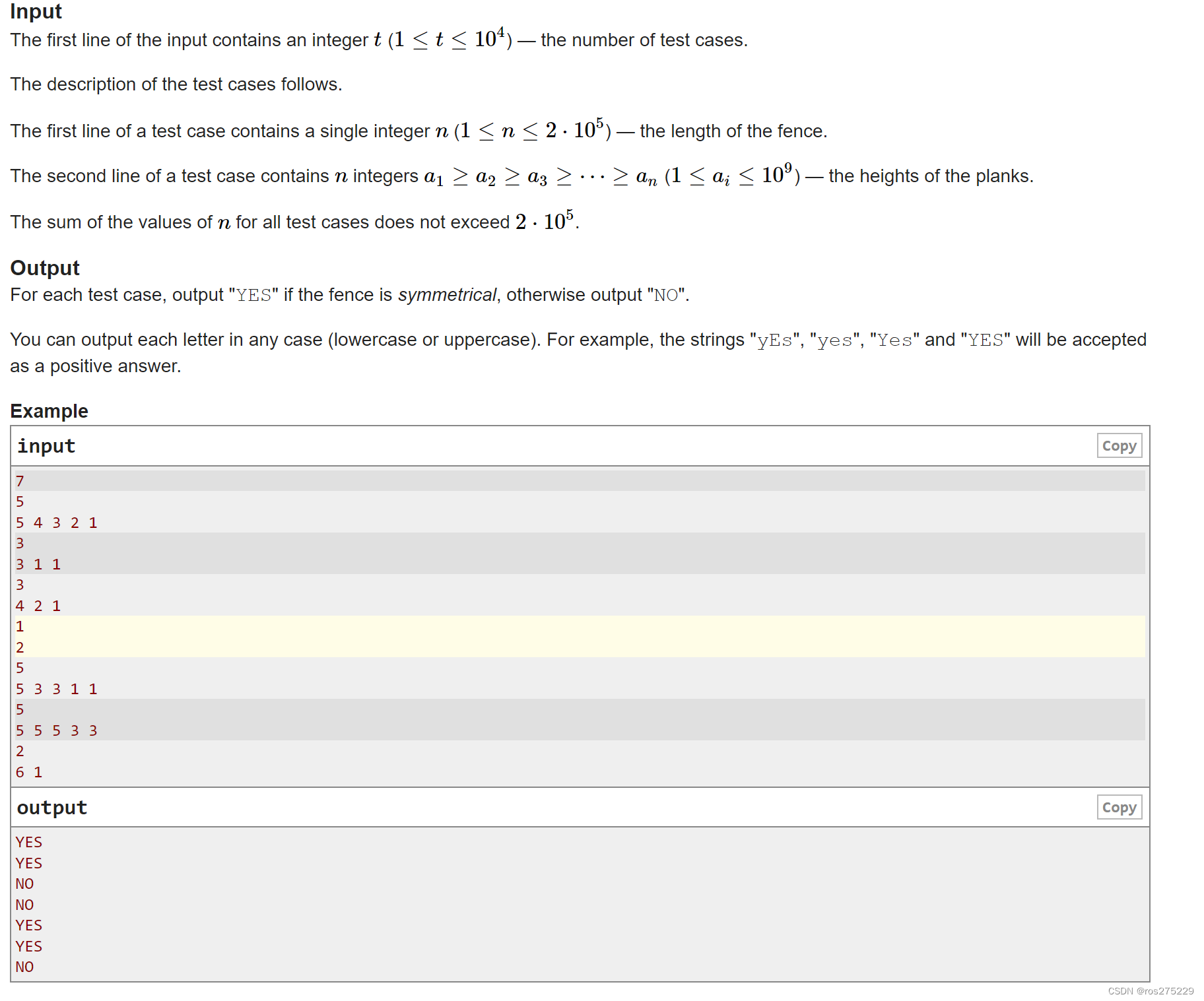
题目意思 :
也就是给你一个非递减数组,数组凑想为一个长度递减围栏,请你该围栏判断是否为一个对称(关于45对称)围栏。
思路 :
先看图 (较潦草hhh):
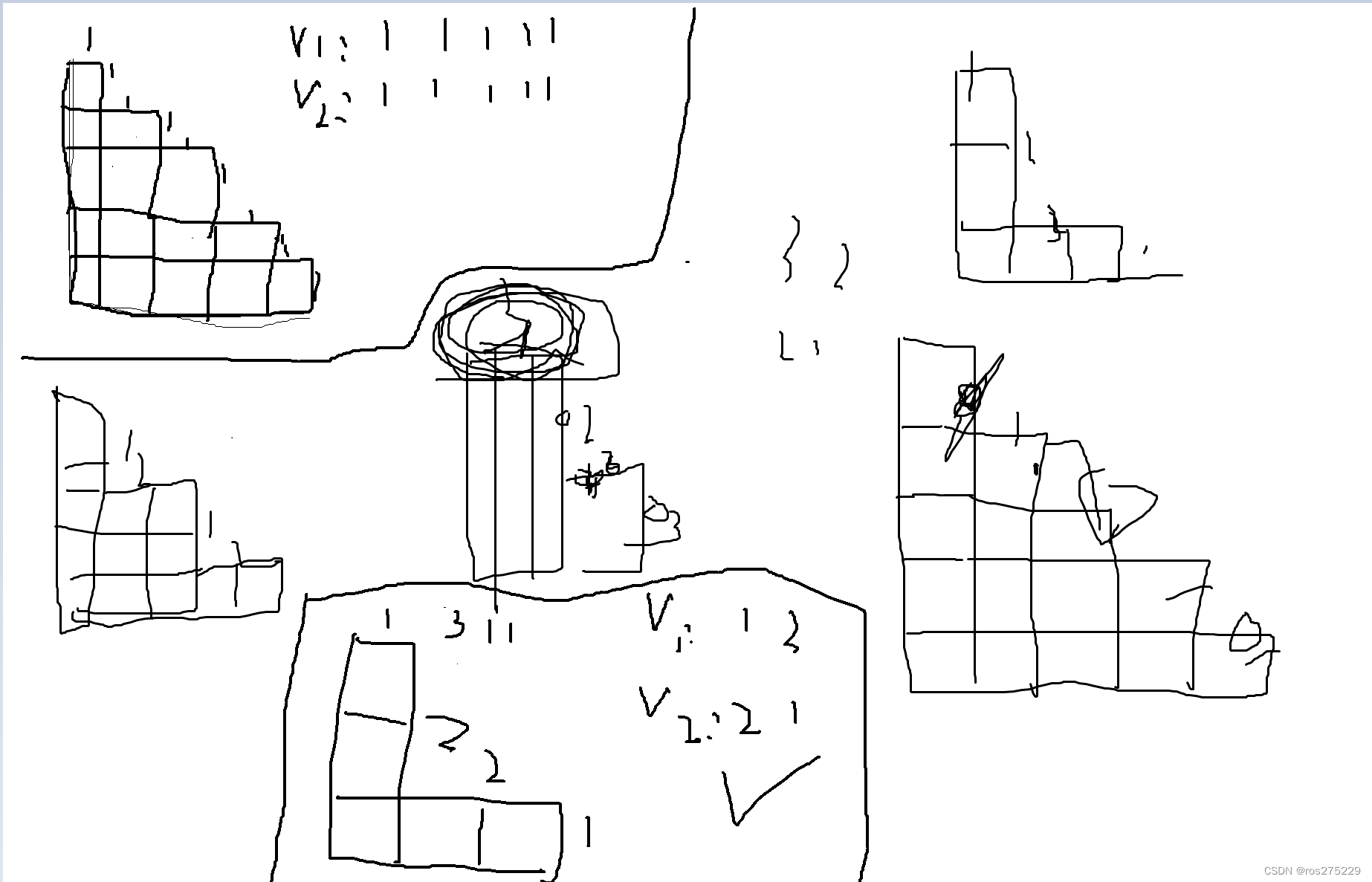
先看左上角的,构建两个vector,v1和v2,v1里面存每层上表面的长度,v2从上往下看存每个纵界面的长度;
例如 :
5
5 4 3 2 1
这个例子 :
v1 : 1 1 1 1 1;
v2 : 1 1 1 1 1;
例如 :
3
3 1 1
这个例子 :
v1 : 1 2;
v2 : 2 1;
最后判断这两个vector是不是能由另一个翻转得到,即可!!! (讲不清楚,自己画图理解,只要两个数组翻转相等,那么就一定围栏对称);
代码 :
// C
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;
typedef long long LL;
const int N = 2e5+10;
int n,a[N];
bool tag;
vector<int> v1;
vector<int> v2;inline void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];a[n+1] = 0;tag = true; v1.clear(); v2.clear();for(int i=1;i<=n;i++){int j = i+1;while(j<=n && a[j]==a[i]) j++;j--;v1.push_back(j-i+1);i = j;}for(int i=1;i<=n;i++){int j = i + 1;while(j<=n && a[j]==a[i]) j++;if(j==n+1) v2.push_back(a[i]);else v2.push_back(a[i]-a[j]);i = j - 1;}
// 测试代码
// for(auto num : v1) cout<<num<<" ";
// cout<<endl;
// for(auto num : v2) cout<<num<<" ";
// cout<<endl;if(v1.size() != v2.size()) tag = false;else {for(int i=0;i<v1.size();i++){if(v1[i] != v2[v1.size()-i-1]){tag = false;break;}}}if(tag) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}int main()
{IOSint _;cin >> _;// _ = 1; while(_ --) solve();return 0;
}好吧,就三题了,hh!!!
相关文章:

Codeforces Round 894 (Div. 3)
还是打一下卡!!! (A,B,C) 目录 A. Gift Carpet 链接 : 题面 : 题目意思 : 思路 : 代码 : B. Sequence Game 链接 : 题面 : 编辑 题目意思 : 思路 : 代码 : C. Flower City Fence 原题链接 : 题面 : 题目意思 : 思路 : 代码 : A. Gift Carpet 链…...
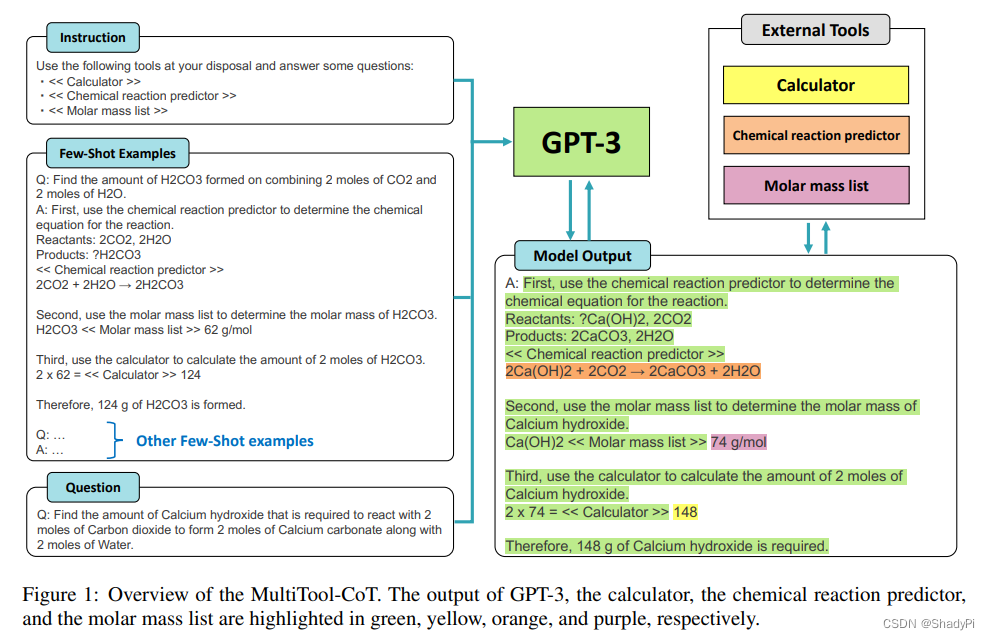
ACL2023 Prompt 相关文章速通 Part 1
Accepted Papers link: ACL2023 main conference accepted papers 文章目录 Accepted PapersPrompter: Zero-shot Adaptive Prefixes for Dialogue State Tracking Domain AdaptationQuery Refinement Prompts for Closed-Book Long-Form QAPrompting Language Models for Lin…...
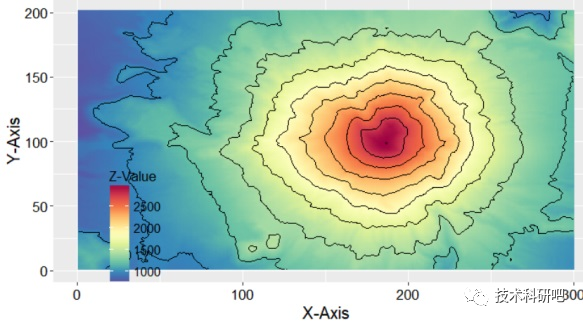
“R语言+遥感“水环境综合评价方法
详情点击链接:"R语言遥感"水环境综合评价方法 一:R语言 1.1 R语言特点(R语言) 1.2 安装R(R语言) 1.3 安装RStudio(R语言) (1)下载地址 &…...
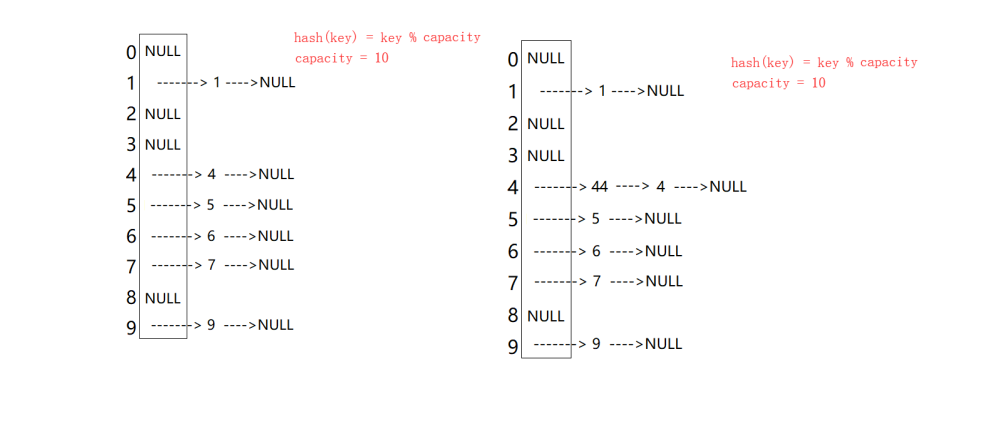
数据结构之哈希
哈希 1. 哈希概念2. 哈希冲突3. 哈希冲突解决3.1 哈希表的闭散列3.2 哈希表的开散列 2. 哈希的应用2.1 位图2.2 布隆过滤器 哈希(Hash)是一种将任意长度的二进制明文映射为较短的二进制串的算法。它是一种重要的存储方式,也是一种常见的检索方…...
-散点图(一))
可视化绘图技巧100篇基础篇(七)-散点图(一)
目录 前言 适用场景 图例 普通散点图与可视化 曲线图 气泡图...

关于什么是框架
框架(Framework)是一个框子——指其约束性,也是一个架子——指其支撑性。 IT语境中的框架,特指为解决一个开放性问题而设计的具有一定 性的支撑结构。在此结构上约束可以根据具体问题扩展、安插更多的组成部分,从而更迅…...

iOS开发Swift-集合类型
集合基本类型:数组 Array (有序), 集合 Set (无序不重复), 字典 Dictionary (无序键值对) 1.数组 Arrays (1)数组的表示 Array<Element> [Element](2)创建空数组 var someInts: [Int] [] someInts.count //数组长度(3)带值数组 var…...
【keepalived双机热备与 lvs(DR)】
目录 一、概述 1.简介 2.原理 3.作用 二、安装 1.配置文件 2.配置项 三、功能模块 1.core 2.vrrp 3.check 四、配置双机热备 1.master 2.backup 五、验证 1.ping验证 2.服务验证 六、双机热备的脑裂现象 七、keepalivedlvs(DR) 1.作…...

C++笔记之静态成员函数可以在类外部访问私有构造函数吗?
C笔记之静态成员函数可以在类外部访问私有构造函数吗? code review! 静态成员函数可以在类外部访问私有构造函数。在C中,访问控制是在编译时执行的,而不是在运行时执行的。这意味着静态成员函数在编译时是与类本身相关联的,而不…...

最新SQLMap进阶技术
SQLMap进阶:参数讲解 (1)–level 5:探测等级。 参数“–level 5”指需要执行的测试等级,一共有5个等级(1~5级),可不加“level”,默认是1级。可以在xml/payloads.xml中看…...
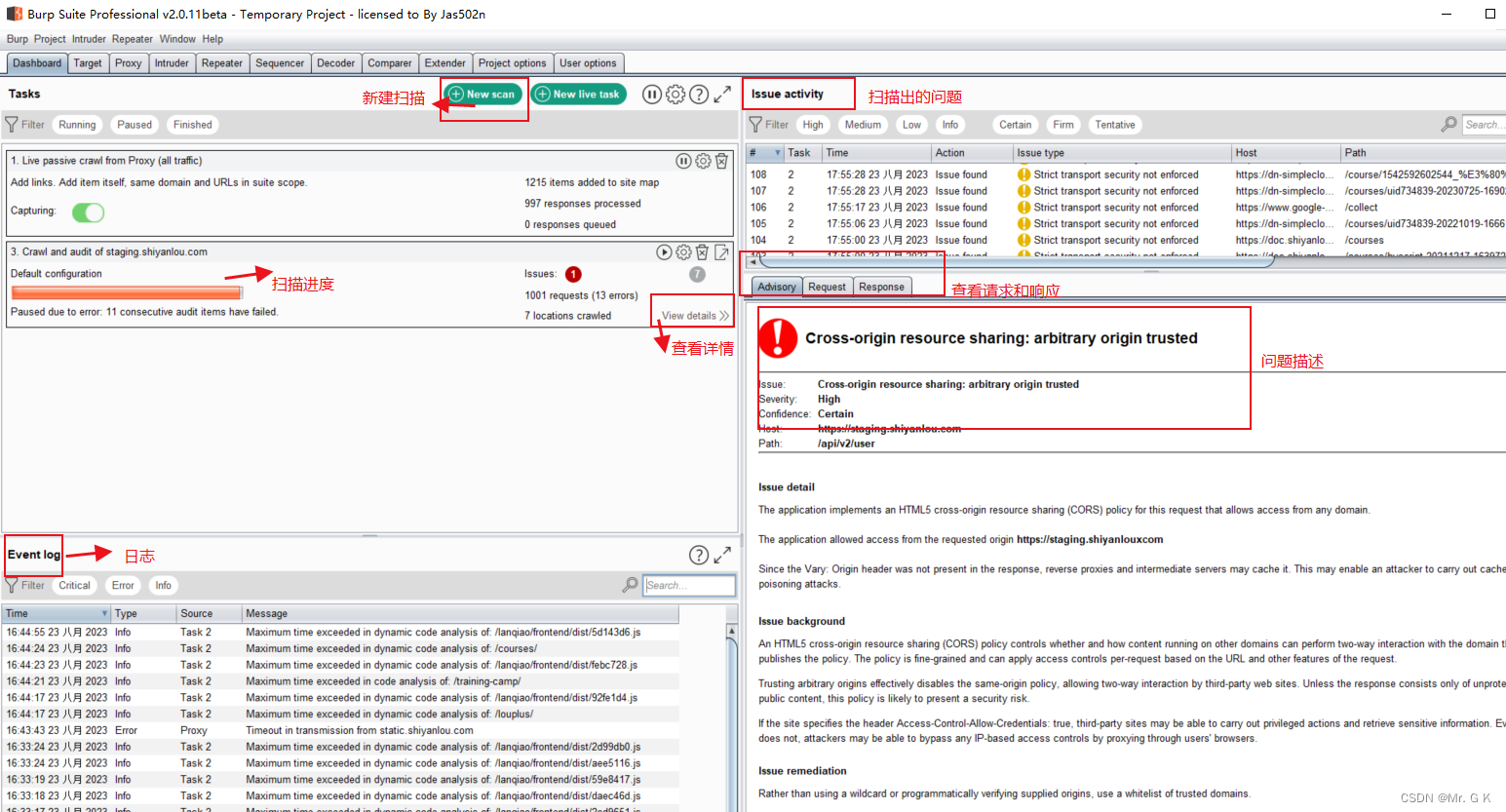
【BurpSuite常用功能介绍】
BurpSuite的使用 1.运行BurpSuite 2.代理设置 打开软件后,我们第一件事就应该去调试软件和浏览器的代理,让BURP能够正常工作抓包 proxy--options,我端口默认使用8080 然后我们打开一个浏览器,进入代理设置 (注意一点࿰…...

Leetcode 108. 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树 分析 给定一个有序数组,要求转换为二叉搜索树。 数组是有序的,并且要求二叉树。 这里看到数组是有序的,马上想到二分,但是又不需要完全二分 实现。 再复习二叉搜索树的结构特点: 左…...

小匠物联联合亚马逊云助力企业数智化出海
如何让家电企业出海产品数智化之路走上康庄大道?8月25日,亚马逊云科技[创新成长企业专列]这趟上云快车将开往宁波站,助力宁波的制造、软件等企业扬帆起航!现场举办“亚马逊云科技助力企业出海数智沙龙”,小匠物联受邀出席。 会议现…...
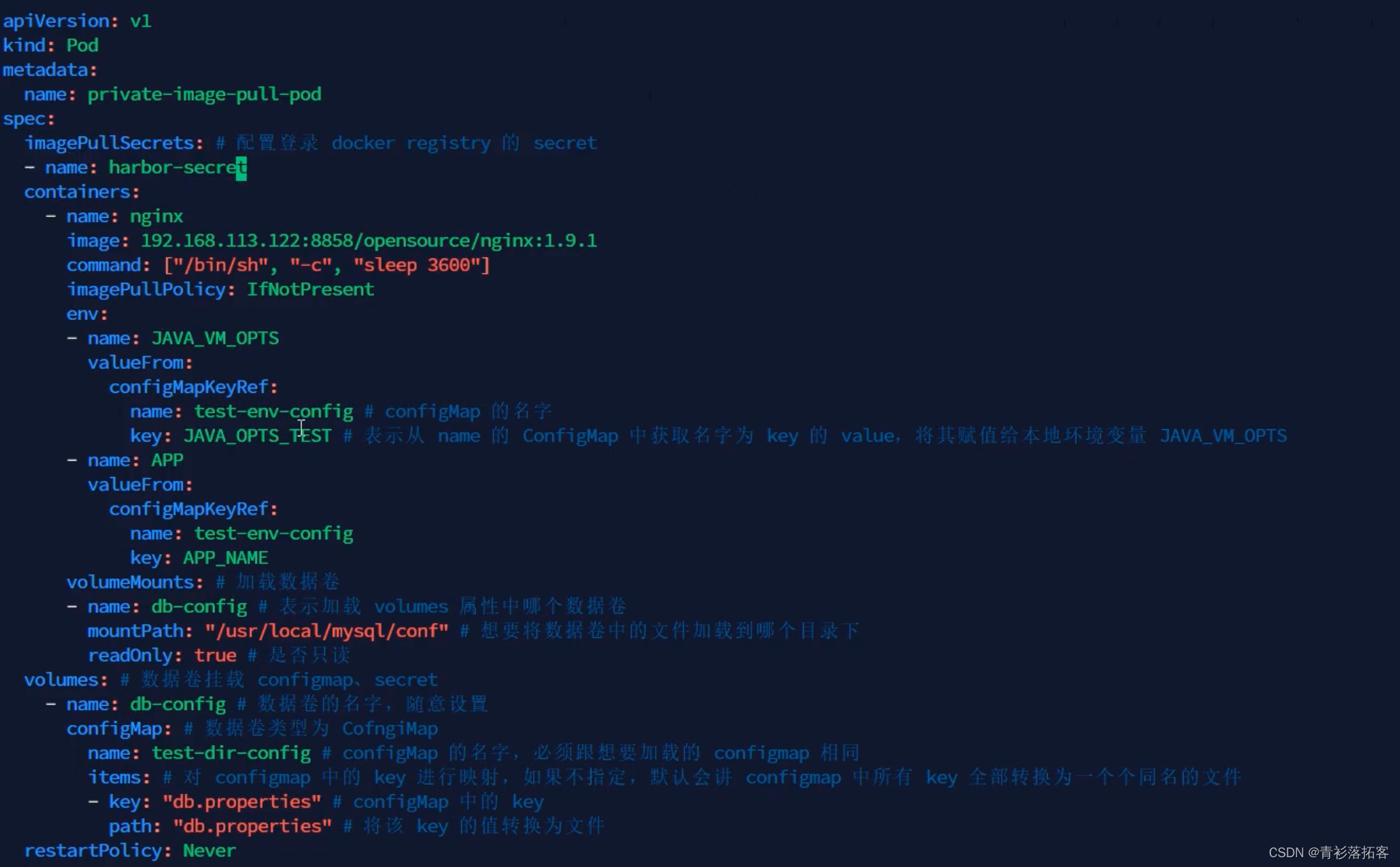
(五)k8s实战-配置管理
一、ConfigMap 使用 kubectl create configmap -h 查看示例,构建 configmap 对象 1) 基于文件夹,加载文件夹下所有配置文件,创建 kubectl create configmap <configmapName> --from-file<dirPath>2) 指定配置文件,创…...
GPT---1234
GPT:《Improving Language Understanding by Generative Pre-Training》 下载地址:https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdfhttps://cdn.openai.com/research-covers/language-unsupervised/language_understa…...
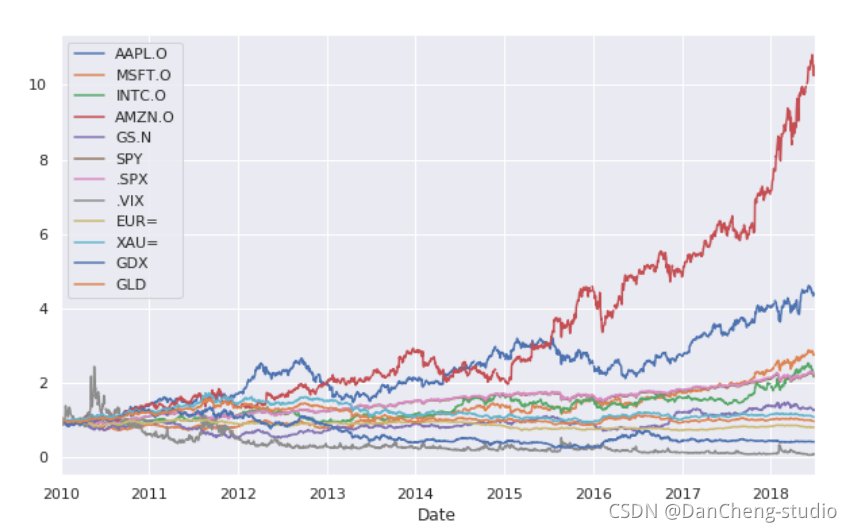
计算机竞赛 基于大数据的时间序列股价预测分析与可视化 - lstm
文章目录 1 前言2 时间序列的由来2.1 四种模型的名称: 3 数据预览4 理论公式4.1 协方差4.2 相关系数4.3 scikit-learn计算相关性 5 金融数据的时序分析5.1 数据概况5.2 序列变化情况计算 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 &…...

python进行数据分析:数据预处理
六大数据类型 见python基本功 import numpy as np import pandas as pd数据预处理 缺失值处理 float_data pd.Series([1.2, -3.5, np.nan, 0]) float_data0 1.2 1 -3.5 2 NaN 3 0.0 dtype: float64查看缺失值 float_data.isna()0 False 1 …...

百度Apollo:引领自动驾驶技术的创新与突破
文章目录 前言一、技术创新二、开放合作三、生态建设四、安全可靠性总结 前言 随着科技的迅猛发展,自动驾驶技术正成为未来交通领域的重要发展方向。在这个领域中,百度Apollo作为中国领先的自动驾驶平台,以其卓越的创新能力和开放合作精神&a…...

Python爬虫 异步、缓存技巧
在进行大规模数据抓取时,Python爬虫的速度和效率是至关重要的。本文将介绍如何通过异步请求、缓存和代理池等技巧来优化Python爬虫的速度和性能。我们提供了实用的方案和代码示例,帮助你加速数据抓取过程,提高爬虫的效率。 使用异步请求、缓…...

YOLOv5屏蔽区域检测(选择区域检测)
YOLOv5屏蔽区域检测以及选择区域检测 前期准备labelme选择mask区域 代码改动 前期准备 思路就是通过一个mask掩膜,对我们想要屏蔽或者选择的区域进行遮挡处理,在推理的时候,将有mask掩膜的图像输入,将最后的结果显示在原始图像上…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

