时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
目录
- 时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
- 预测效果
- 基本介绍
- 模型介绍
- 程序设计
- 参考资料
- 致谢
预测效果


基本介绍
MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)(完整源码和数据)
模型介绍
PSO-KELM,常用于时间序列预测任务。
PSO是一种基于群体智能的优化算法,它模拟了鸟群觅食的行为。在PSO中,每个个体被称为粒子,代表了解空间中的一个候选解。粒子通过在解空间中搜索来寻找最优解,同时根据个体最优和全局最优的信息进行调整和更新。PSO算法通过迭代更新粒子的位置和速度来逐步优化解的质量。
PSO-KELM的时间序列预测步骤如下:
准备时间序列数据集,将其划分为训练集和测试集。
初始化PSO算法的粒子群,并随机初始化粒子的位置和速度。
对于每个粒子,使用KELM算法,其中隐藏层的连接权重和偏置通过PSO进行优化。
根据训练得到的模型,对测试集进行预测。
评估预测结果的准确性。
根据预测准确性和PSO的优化目标,更新粒子的速度和位置。
重复步骤3至步骤6,直到达到预定的迭代次数或满足停止准则。
根据最优的粒子位置得到最终的连接权重和偏置,用于进行时间序列的预测。
需要注意的是,PSO-KELM算法的性能和结果可能会受到参数设置的影响,例如粒子数、迭代次数、网络的隐藏层节点数等。因此,在实际应用中需要根据具体问题进行调优和参数选择。
程序设计
- 完整程序和数据下载地址方式:私信博主回复MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比。
%% 各算法对比
clc;clear;close all
%%Positions = initialization(SearchAgents_no, dim, ub, lb);%% 用于记录迭代曲线
Convergence_curve = zeros(1, Max_iteration);
%% 循环计数器
iter = 0;%% 优化算法主循环
while iter < Max_iteration % 对迭代次数循环for i = 1 : size(Positions, 1) % 遍历Flag4ub = Positions(i, :) > ub;Flag4lb = Positions(i, :) < lb;% 若的位置在最大值和最小值之间,则位置不需要调整,若超出最大值,最回到最大值边界% 若超出最小值,最回答最小值边界Positions(i, :) = (Positions(i, :) .* (~(Flag4ub + Flag4lb))) + ub .* Flag4ub + lb .* Flag4lb; % 计算适应度函数值
% Positions(i, 2) = round(Positions(i, 2));
% fitness = fical(Positions(i, :));fitness = fobj(Positions(i, :));% 更新 Alpha, Beta, Deltaif fitness < Alpha_score % 如果目标函数值小if fitness > Alpha_score && fitness > Beta_score && Delta_score = fitness; % 则将Delta的目标函数值更新为最优目标函数值Delta_pos = Positions(i, :); % 同时更新Delta的位置endend% 线性权重递减wa = 2 - iter * ((2) / Max_iteration); % 更新搜索群的位置for i = 1 : size(Positions, 1) % 遍历每个for j = 1 : size(Positions, 2) % 遍历每个维度% 包围猎物,位置更新r1 = rand; % r1 is a random number in [0,1]r2 = rand; % r2 is a random number in [0,1]A1 = 2 * wa * r1 - wa; % 计算系数A,Equation (3.3)C1 = 2 * r2; % 计算系数C,Equation (3.4)% Alpha 位置更新D_alpha = abs(C1 * Alpha_pos(j) - Positions(i, j)); % Equation (3.5)-part 1X1 = Alpha_pos(j) - A1 * D_alpha; % Equation (3.6)-part 1r1 = rand; % r1 is a random number in [0,1]r2 = rand; % r2 is a random number in [0,1]A2 = 2 * wa * r1 - wa; % 计算系数A,Equation (3.3)C2 = 2 *r2; % 计算系数C,Equation (3.4)% Beta 位置更新D_beta = abs(C2 * Beta_pos(j) - Positions(i, j)); % Equation (3.5)-part 2X2 = Beta_pos(j) - A2 * D_beta; % Equation (3.6)-part 2 r1 = rand; % r1 is a random number in [0,1]r2 = rand; % r2 is a random number in [0,1]A3 = 2 *wa * r1 - wa; % 计算系数A,Equation (3.3)C3 = 2 *r2; % 计算系数C,Equation (3.4)% Delta 位置更新D_delta = abs(C3 * Delta_pos(j) - Positions(i, j)); % Equation (3.5)-part 3X3 = Delta_pos(j) - A3 * D_delta; % Equation (3.5)-part 3% 位置更新Positions(i, j) = (X1 + X2 + X3) / 3; % Equation (3.7)endend% 更新迭代器iter = iter + 1; Convergence_curve(iter) = Alpha_score;curve(iter)=sum(Convergence_curve)/iter;disp(['第',num2str(iter),'次迭代'])disp(['current iteration is: ',num2str(iter), ', best fitness is: ', num2str(Alpha_score)]);
end%% 记录最佳参数
% best_lr = Alpha_pos(1, 1);
% best_hd = Alpha_pos(1, 2);
% best_l2 = Alpha_pos(1, 3);
end
function result(true_value,predict_value,type)
disp(type)
rmse=sqrt(mean((true_value-predict_value).^2));
disp(['根均方差(RMSE):',num2str(rmse)])
mae=mean(abs(true_value-predict_value));
disp(['平均绝对误差(MAE):',num2str(mae)])
mape=mean(abs((true_value-predict_value)./true_value));
disp(['平均相对百分误差(MAPE):',num2str(mape*100),'%'])
r2 = R2(predict_value, true_value);
disp(['R平方决定系数(MAPE):',num2str(r2)])
nse = NSE(predict_value, true_value);
disp(['纳什系数(NSE):',num2str(nse)])fprintf('\n')
参考资料
[1] https://blog.csdn.net/kjm13182345320?spm=1010.2135.3001.5343
[2] https://mianbaoduo.com/o/bread/mbd-YpiamZpq
[3] SI Y W,YIN J. OBST-based segmentation approach to financial time series[J]. Engineering Applications of Artificial Intelligence,2013,26( 10) : 2581-2596.
[4] YUAN X,CHEN C,JIANG M,et al. Prediction Interval of Wind Power Using Parameter Optimized Beta Distribution Based LSTM Model[J]. Applied Soft Computing,2019,82:105550.143
致谢
- 大家的支持是我写作的动力!
- 感谢大家订阅,记得备注!
相关文章:

时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)
时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比) 目录 时序预测 | MATLAB实现PSO-KELM粒子群算法优化核极限学习机时间序列预测(含KELM、ELM等对比)预测效果基本介绍模型介绍程序设计参…...
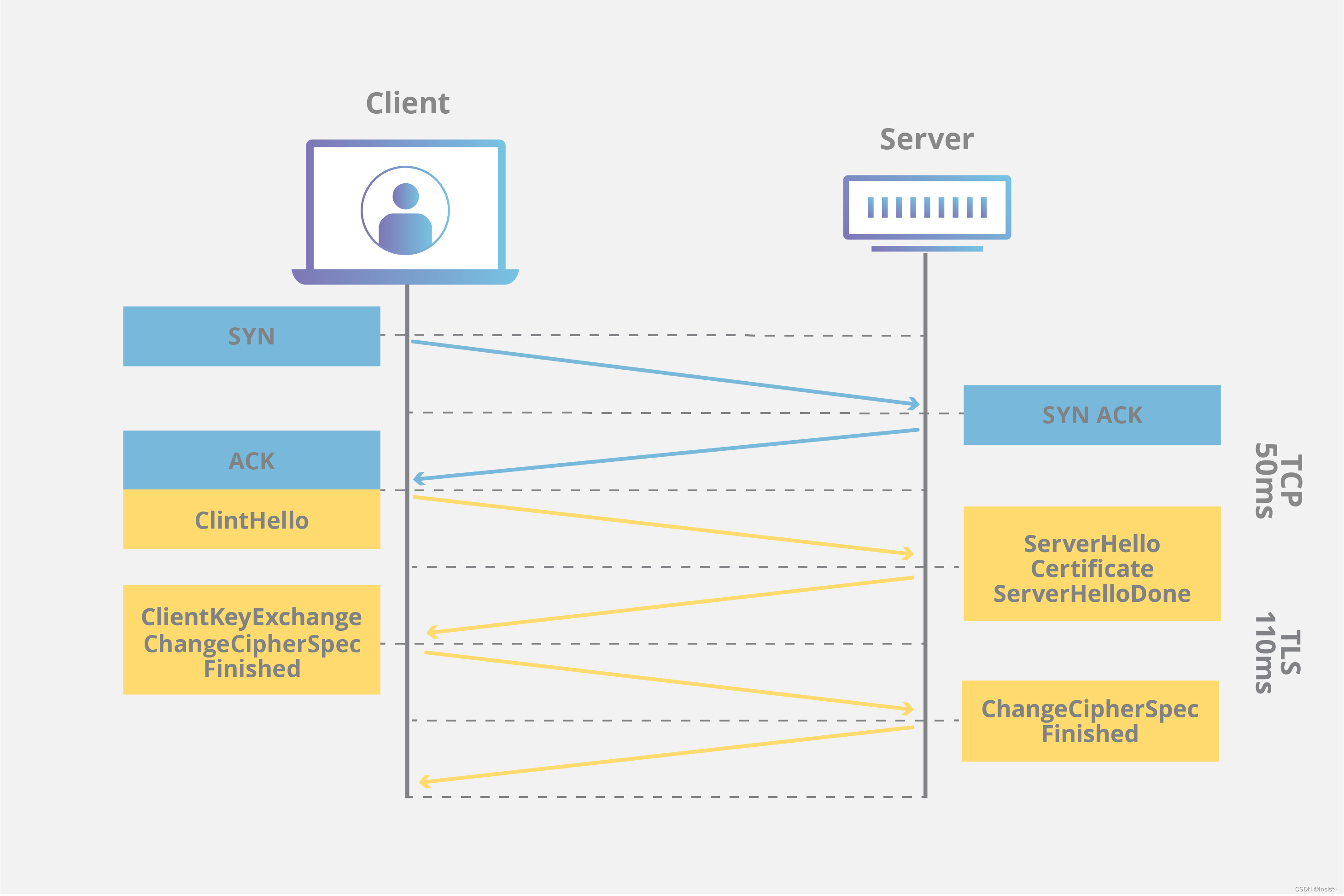
SSL/TLS协议的概念、工作原理、作用以及注意事项
个人主页:insist--个人主页 本文专栏:网络基础——带你走进网络世界 本专栏会持续更新网络基础知识,希望大家多多支持,让我们一起探索这个神奇而广阔的网络世界。 目录 一、SSL/TLS协议的基本概念 二、SSL/TLS的工作…...
[Stable Diffusion教程] 第一课 原理解析+配置需求+应用安装+基本步骤
第一课 原理解析配置需求应用安装基本步骤 本次内容记录来源于B站的一个视频 以下是自己安装过程中整理的问题及解决方法: 问题:stable-diffusion-webui启动No Python at ‘C:\xxx\xxx\python.exe‘ 解答:打开webui.bat 把 if not de…...

uniapp结合Canvas+renderjs根据经纬度绘制轨迹(二)
uniapp结合Canvasrenderjs根据经纬度绘制轨迹 文章目录 uniapp结合Canvasrenderjs根据经纬度绘制轨迹效果图templaterenderjsjs数据结构 根据官方建议要想在 app-vue 流畅使用 Canvas 动画,需要使用 renderjs 技术,把操作canvas的js逻辑放到视图层运…...

VR全景加盟会遇到哪些问题?全景平台会提供什么?
想创业,你是否也遇到这些问题呢?我是外行怎么办?没有团队怎么办?项目回本周期快吗?项目靠谱吗?加盟平台可信吗?等等这类疑问。近几年,VR产业发展迅速,尤其是VR全景项目在…...

如何进行微服务的集成测试
集成测试的概念 说到集成测试,相信每个测试工程师并不陌生,它不是一个崭新的概念,通过维基百科定义可以知道它在传统软件测试中的含义。 Integration testing (sometimes called integration and testing, abbreviated I&T) is the pha…...

spark grpc 在master运行报错 exitcode13 User did not initialize spark context
程序使用sparksql 以及protobuf grpc ,执行报错 ApplicationMaster: Final app status: FAILED, exitCode: 13, (reason: Uncaught exception: java.lang.IllegalStateException: User did not initialize spark context! 先说原因 : 1.使用了不具备权限…...

nginx 反向代理的原理
Nginx(发音为"engine X")是一个高性能、轻量级的开源Web服务器和反向代理服务器。它的反向代理功能允许将客户端的请求转发到后端服务器,然后将后端服务器的响应返回给客户端。下面是Nginx反向代理的工作原理: 1.客户端…...

【SpringBoot】第二篇:RocketMq使用
背景: 本文会介绍多种案例,教大家如何使用rocketmq。 一般rocketmq使用在微服务项目中,属于分模块使用。这里使用springboot单体项目来模拟使用。 本文以windows系统来做案例。 下载rocketmq和启动: RocketMQ 在 windows 上运行…...

飞天使-vim简单使用技巧
此文是记录技巧使用,如果想节约时间,可以直接看最后一个章节 vim 的介绍 vim号称编辑器之神,唯快不破,可扩展,各种插件满天飞。 vi 1991 vim 1.14 vim四种模式 普通模式: 移动光标, 删除文本,…...

分布式搜索引擎----elasticsearch
目录 1、初识elasticsearch 1.1、什么是elasticsearch 1.2.ELK技术栈 2、正向索引和倒排索引 2.1、正向索引 2.2、倒排索引 2.3、正向索引和倒排索引的区别 3、elasticsearch中的概念理解 3.1、文档和字段 3.2、索引和映射 3.3、mysql与elasticsearch 1、初识elasti…...

AnnotationConfigApplicationContext类和ClasspathXmlApplicationContext类的区别?
在 Spring Framework 中,AnnotationConfigApplicationContext 和 ClasspathXmlApplicationContext 是两个不同的应用程序上下文实现,用于配置和管理 Spring Bean 容器。它们之间的主要区别在于配置的方式和使用场景。 1. **AnnotationConfigApplication…...
使用VSCode SSH实现公网远程连接本地服务器开发的详细教程
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...
Codeforces Round 894 (Div. 3)
还是打一下卡!!! (A,B,C) 目录 A. Gift Carpet 链接 : 题面 : 题目意思 : 思路 : 代码 : B. Sequence Game 链接 : 题面 : 编辑 题目意思 : 思路 : 代码 : C. Flower City Fence 原题链接 : 题面 : 题目意思 : 思路 : 代码 : A. Gift Carpet 链…...
ACL2023 Prompt 相关文章速通 Part 1
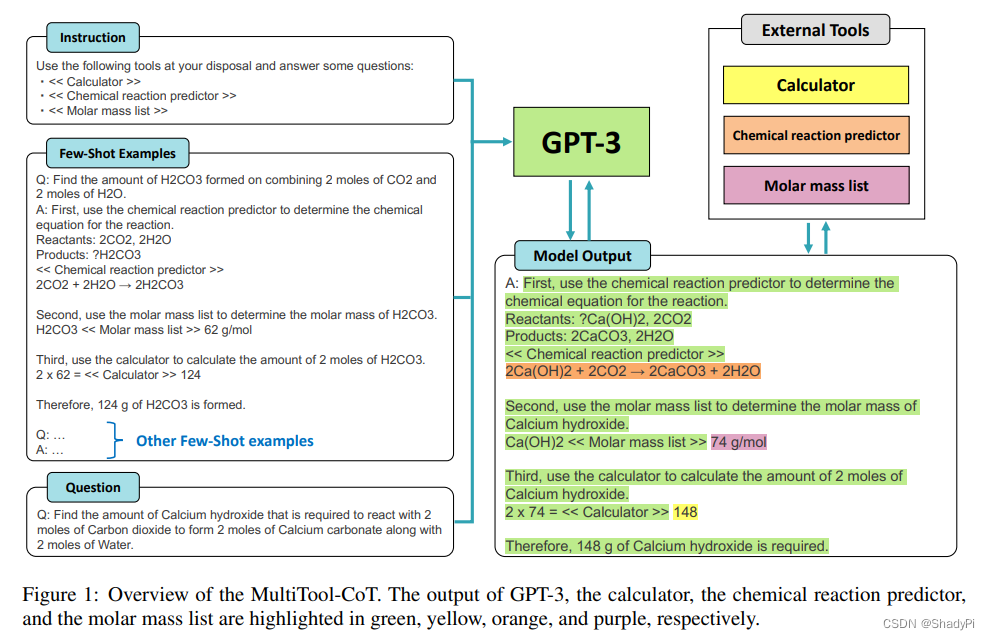
Accepted Papers link: ACL2023 main conference accepted papers 文章目录 Accepted PapersPrompter: Zero-shot Adaptive Prefixes for Dialogue State Tracking Domain AdaptationQuery Refinement Prompts for Closed-Book Long-Form QAPrompting Language Models for Lin…...
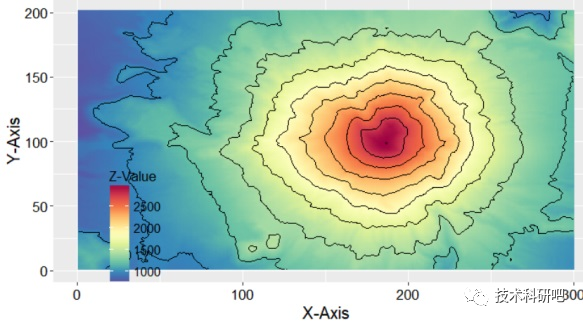
“R语言+遥感“水环境综合评价方法
详情点击链接:"R语言遥感"水环境综合评价方法 一:R语言 1.1 R语言特点(R语言) 1.2 安装R(R语言) 1.3 安装RStudio(R语言) (1)下载地址 &…...
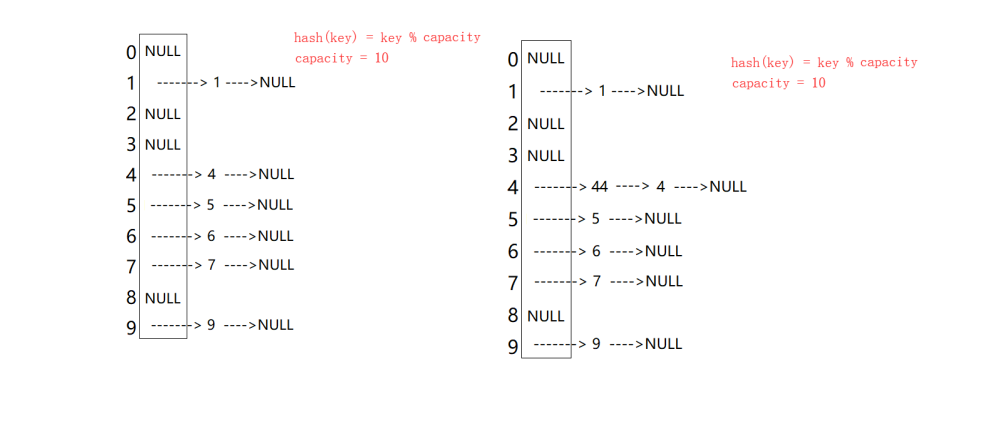
数据结构之哈希
哈希 1. 哈希概念2. 哈希冲突3. 哈希冲突解决3.1 哈希表的闭散列3.2 哈希表的开散列 2. 哈希的应用2.1 位图2.2 布隆过滤器 哈希(Hash)是一种将任意长度的二进制明文映射为较短的二进制串的算法。它是一种重要的存储方式,也是一种常见的检索方…...
-散点图(一))
可视化绘图技巧100篇基础篇(七)-散点图(一)
目录 前言 适用场景 图例 普通散点图与可视化 曲线图 气泡图...

关于什么是框架
框架(Framework)是一个框子——指其约束性,也是一个架子——指其支撑性。 IT语境中的框架,特指为解决一个开放性问题而设计的具有一定 性的支撑结构。在此结构上约束可以根据具体问题扩展、安插更多的组成部分,从而更迅…...

iOS开发Swift-集合类型
集合基本类型:数组 Array (有序), 集合 Set (无序不重复), 字典 Dictionary (无序键值对) 1.数组 Arrays (1)数组的表示 Array<Element> [Element](2)创建空数组 var someInts: [Int] [] someInts.count //数组长度(3)带值数组 var…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
