积跬步至千里 || 数学基础、算法与编程
数学基础、算法与编程
1. BAP 技能
BAP 技能是指基础(Basic)、算法(Algorithm)和编程(Programm)三种基本技能的深度融合。理工科以数学、算法与编程为根基,这三个相辅相成又各有区别。
-
(1)数学以线性代数为主要研究工具和部分微积分技术为手段,来实现优化的目标。
-
(2)算法是应用数学和各类数据分析方法的灵魂,搭建了数学与应用领域的之间的桥梁,通常是一种真实解的逼近过程,其中主要涉及到矩阵的运算。
-
(3)编程泛指一切的计算机语言,通过循环迭代的方式编制出计算过程,如Matlab、Python、C++等,其中会有众多的库可以调用,如scikit-learn、CVX优化库、OpenCV图像处理库等等。
注意:算法和编程是两个严格区分的领域,算法需要深厚的数学功底,编程需要的是简单逻辑。
2. 传统算法
一类常见的算法是误差项 f ( x , w ) f(\boldsymbol{x},\boldsymbol{w}) f(x,w) 和复杂度测度项 g ( w ) g(\boldsymbol{w}) g(w) 的折衷,形如
min w f ( x , w ) + g ( w ) \min_{\boldsymbol{w}}\;f(\boldsymbol{x},\boldsymbol{w})+g(\boldsymbol{w}) wminf(x,w)+g(w)
常见的误差项,又称损失函数有以下几种(以回归问题为例)
- 平方损失
f ( x , w ) = ∥ X w − b ∥ 2 2 = ∑ i ( w i x i − b i ) 2 f(\boldsymbol{x},\boldsymbol{w})=\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_2^2=\sum_i(w_ix_i-b_i)^2 f(x,w)=∥Xw−b∥22=i∑(wixi−bi)2
- 绝对值损失
f ( x , w ) = ∥ X w − b ∥ 1 = ∑ i ∣ b i − w i x i ∣ f(\boldsymbol{x},\boldsymbol{w})=\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_1=\sum_i\Big\vert b_i-w_ix_i\Big\vert f(x,w)=∥Xw−b∥1=i∑ bi−wixi
- Hubber 损失
Huber = { 1 2 e i 2 ∣ e i ∣ < δ δ ∣ e i ∣ − 1 2 δ 2 Otherwise \text{Huber}=\left\{ \begin{array}{lcl} \frac{1}{2}e_i^2 & & \vert e_i\vert<\delta\\ \delta\vert e_i\vert -\frac{1}{2}\delta^2 & & \text{Otherwise} \end{array} \right. Huber={21ei2δ∣ei∣−21δ2∣ei∣<δOtherwise
# huber 损失
def huber(e, delta):loss = np.where(np.abs(e) < delta , 0.5*(e**2), delta*np.abs(e) - 0.5*(delta**2))return lossimport numpy as np
import matplotlib.pyplot as plte = np.arange(0,5,0.1)
z1 = 0.5*e**2
z2 = np.abs(e)
z3 = huber(e,1)
z4 = np.log(1+np.abs(e))plt.plot(e,z1,label='L2')
plt.plot(e,z2,label='L1')
plt.plot(e,z3,label='Huber')
plt.plot(e,z4,label='Hx')
plt.title('Loss Function')
plt.axis([0,5,0,12])
plt.legend()
plt.xlabel('e')
plt.ylabel('Eerror')
plt.show()
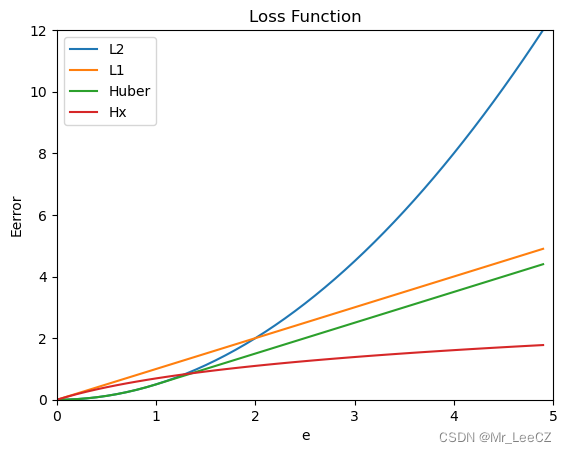
常见的目标函数
min w ∥ X w − b ∥ 2 2 + ∥ w ∥ 2 2 \min_{\boldsymbol{w}}\;\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_2^2+\Vert \boldsymbol{w}\Vert_2^2 wmin∥Xw−b∥22+∥w∥22
min w ∥ X w − b ∥ 2 2 + ∥ w ∥ 1 \min_{\boldsymbol{w}}\;\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_2^2+\Vert \boldsymbol{w}\Vert_1 wmin∥Xw−b∥22+∥w∥1
min w ∥ X w − b ∥ 1 \min_{\boldsymbol{w}}\;\Vert X\boldsymbol{w}-\boldsymbol{b}\Vert_1 wmin∥Xw−b∥1
min w ∥ X − U V T ∥ F 2 , s . t . U ≥ 0 , V ≥ 0 \min_{\boldsymbol{w}}\;\Vert X-UV^T\Vert_F^2,\;\;\;s.t.\;\;U\geq0,V\geq 0 wmin∥X−UVT∥F2,s.t.U≥0,V≥0
min w ∥ X − U V T ∥ 1 , s . t . U ≥ 0 , V ≥ 0 \min_{\boldsymbol{w}}\;\Vert X-UV^T\Vert_1,\;\;\;s.t.\;\;U\geq0,V\geq 0 wmin∥X−UVT∥1,s.t.U≥0,V≥0
min w ∥ X − U V T ∥ 2 , 1 , s . t . U ≥ 0 , V ≥ 0 \min_{\boldsymbol{w}}\;\Vert X-UV^T\Vert_{2,1},\;\;\;s.t.\;\;U\geq0,V\geq 0 wmin∥X−UVT∥2,1,s.t.U≥0,V≥0
min w ∥ X − U V T ∥ 2 , 1 + ∥ U ∥ 1 , s . t . U ≥ 0 , V ≥ 0 \min_{\boldsymbol{w}}\;\Vert X-UV^T\Vert_{2,1}+\Vert U\Vert_1,\;\;\;s.t.\;\;U\geq0,V\geq 0 wmin∥X−UVT∥2,1+∥U∥1,s.t.U≥0,V≥0
min w ∥ X − U V T ∥ 2 , 1 + ∥ U ∥ ∗ , s . t . U ≥ 0 , V ≥ 0 \min_{\boldsymbol{w}}\;\Vert X-UV^T\Vert_{2,1}+\Vert U\Vert_*,\;\;\;s.t.\;\;U\geq0,V\geq 0 wmin∥X−UVT∥2,1+∥U∥∗,s.t.U≥0,V≥0
可通过一些优化工具箱或者优化工具进行求解
3. 网络优化
通过神经网络或者深度学习进行优化
相关文章:

积跬步至千里 || 数学基础、算法与编程
数学基础、算法与编程 1. BAP 技能 BAP 技能是指基础(Basic)、算法(Algorithm)和编程(Programm)三种基本技能的深度融合。理工科以数学、算法与编程为根基,这三个相辅相成又各有区别。 (1)数学以线性代数为主要研究工具和部分微积分技术为手…...
Java单元测试 JUnit 5 快速上手
一、背景 什么是 JUnit 5?首先就得聊下 Java 单元测试框架 JUnit,它与另一个框架 TestNG 占据了 Java领域里单元测试框架的主要市场,其中 JUnit 有着较长的发展历史和不断演进的丰富功能,备受大多数 Java 开发者的青睐。 而说到…...

【Linux网络】TCP UDP socket HTTP webSocket之间的区别
目录 一、OSI & TCP/IP模型 二、几者之间的关系 三、HTTP 四、Socket 五、WebSocket 5.1、WebSocket 优点 一、OSI & TCP/IP模型 首先我们要了解OSI七层模型,和预支对应的TCP/IP 四层的模型。 用下面的图可以看出,TCP UDP 工作在传输层&…...

【面向大一新生IT技术社群招新啦,不来瞅瞅?】
个人名片: 🐼作者简介:一名大三在校生 🐻❄️个人主页:落798. 🐼个人WeChat:落798. 🕊️系列专栏:【零基础学java】 ----- 【重识c语言】 ---- 【计算机网络】—【Spri…...

分析系统 - 使用Python爬虫
在竞争激烈的市场环境中,了解和分析竞争对手的销售策略和市场表现对于企业的成功至关重要。本文将介绍如何利用Python爬虫建立低成本的销售竞争对手分析系统,探索其方法、工具和好处,并同时解决可能出现的问题。 销售竞争对手分析的目标是获取…...
strstr函数
目录 函数介绍: 函数分析: 使用案例: 函数介绍: 返回指向 str1 中第一次出现的 str2 的指针,如果 str2 不是 str1 的一部分,则返回一个空指针。 匹配过程不包括终止空字符,但它到此为止。 …...

[C++] string类常用接口的模拟实现
文章目录 1、前言2、遍历2.1 operator[ ]下标方式2.2 迭代器2.3 范围for2.4 c_str 3、容量相关3.1 size(大小)3.2 capacity(容量)3.3 empty(判空)3.4 clear(清理)3.5 reserve3.6 res…...

每日一学——防火墙
防火墙是网络安全的重要组成部分,可以帮助保护网络免受恶意攻击和未经授权的访问。以下是防火墙的基本配置步骤: 定义安全策略:防火墙通过安全策略来决定允许或拒绝网络流量。你需要定义适当的安全策略来保护你的网络。安全策略通常包括源IP地…...

常用数据库备份方法,sql数据库备份方法
在信息时代,数据成为了公司的主要资产。然而,数据的安全性和完整性也成为企业管理的重要组成部分。因此,数据库备份至关重要。本文将详细介绍几种常见的数据库备份方法。 全备份 全备份是指数据库中所有数据的备份,包括数据文件、…...

常见前端面试之VUE面试题汇总八
22. Vue 子组件和父组件执行顺序 加载渲染过程: 1.父组件 beforeCreate 2.父组件 created 3.父组件 beforeMount 4.子组件 beforeCreate 5.子组件 created 6.子组件 beforeMount 7.子组件 mounted 8.父组件 mounted 更新过程: 1. 父组件 befor…...

弯道超车必做好题集锦二(C语言选择题)
前言: 编程想要学的好,刷题少不了,我们不仅要多刷题,还要刷好题!为此我开启了一个弯道超车必做好题锦集的系列,每篇大约10题左右。此为第二篇选择题篇,该系列会不定期更新,后续还会…...
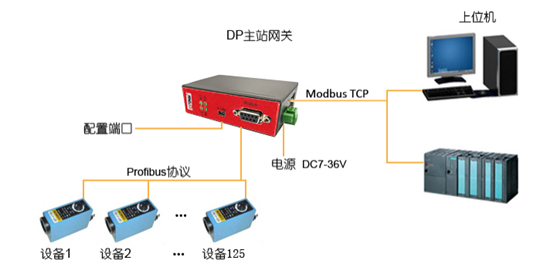
PROFIBUS主站转MODBUS TCP网关
1.产品功能 YC-DPM-TCP网关在Profibus总线侧实现主站功能,在以太网侧实现ModbusTcp服务器功能。可将Profibus DP从站接入到ModbusTcp网络;通过增加DP/PA耦合器,也可将Profibus PA从站接入ModbusTcp网络。YC-DPM-TCP网关最多支持125个Profibu…...
【力扣】盛最多水的容器
目录 题目 题目初步解析 水桶效应 代码实现逻辑 第一步 第二步 第三步 代码具体实现 注意 添加容器元素的函数 计算迭代并且判断面积是否是最大值 总代码 运行结果 总结 题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是…...
【SQL应知应会】索引(三)• MySQL版:聚簇索引与非聚簇索引;查看索引与删除索引;索引方法
欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享,与更多的人进行学习交流 本文收录于SQL应知应会专栏,本专栏主要用于记录对于数据库的一些学习,有基础也有进阶,有MySQL也有Oracle 索引 • MySQL版 前言一、索引1.简介2.索引类型之逻…...
rtmp直播
技术要求:nginxnginx-rtmpffmpegVLC 跟着大佬走的: 传送门 准备工作: 首先需要一台公网ip的服务器 这是使用天翼云的弹性云主机:免费试用1个月 天翼云官网 点击关机,更多里面选择重置密码, 默认用户名为…...

4.14 tcp_tw_reuse 为什么默认是关闭的?
开启 tcp_tw_reuse 参数可以快速复用处于 TIME_WAIT 状态的 TCP 连接时,相当于缩短了 TIME_WAIT 状态的持续时间。 tcp_tw_reuse 是什么? TIME_WAIT 状态的持续时间是 60 秒,这意味着这 60 秒内,客户端一直会占用着这个端口。端…...

Python数据分析和爬虫:解析数据的强大工具
引言: 在当今数据爆炸的时代,数据分析和数据提取变得越来越重要。作为一种简洁而强大的编程语言,Python在数据分析和爬虫领域有着广泛的应用。本文将详细介绍Python在数据分析和爬虫中的常用库和技术,并探讨其在实际应用中的优势…...
)
机器学习之SGD(Stochastic Gradient Descent,随机梯度下降)
SGD(Stochastic Gradient Descent,随机梯度下降)是深度学习中最基本的优化算法之一。它是一种迭代式的优化方法,用于训练神经网络和其他机器学习模型。以下是关于SGD优化器的重要信息: 基本原理:SGD的基本思…...

leetcode做题笔记100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 思路一: bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p NULL &…...

【Hadoop】Hadoop入门概念简介
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,Java基础学习,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
