算法通关村——数论经典问题解析
1. 辗转相除法
主要目的是获取两个数里面的最大公约数。
public int gcd(int a, int b) {int k = 0;do {k = a % b;a = b;b = k;} while (k != 0);return a;}
2. 素数和合数
素数的要求是必须大于等于2,并且只能被1和它本身整除。
判断的方法比较简单,就是从2开始到n一直相除,判断是否等于0。但是其实可以不需要判断到n,到根号n即可。
public boolean isPrim(int num) {for (int i = 2; i <= Math.sqrt(num); i++) {if (num % i == 0) {return false;}}return true;}
2.1 计数质数
计数质数
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入:n = 0
输出:0
示例 3:
输入:n = 1
输出:0
2.2 枚举法
质数的定义:除了1和它本身,没有其余的因数。而这道题目是用来同一某个元素内出现质数的个数,只需要再添加一个循环,用于判断每个数是否是质数,是就加一,而判断方法就是上面的方法。
public int countPrimes(int n) {int count =0;for(int i=2;i<n;i++){if(isPrim(i)){count ++;}}return count;}public boolean isPrim(int n){for(int i=2;i<=Math.sqrt(n);i++){if(n % i == 0){return false;}}return true;}
不过这样写是力扣测试通过不了,效率太低。
3. 埃氏筛
定义:如果 xxx 是质数,那么大于 xxx 的 xxx 的倍数 2x,3x,…2x,3x,\ldots2x,3x,… 一定不是质数,因此我们可以从这里入手。
例如 2是素数,那么2的倍数一定不是素数,3也是同理,只需要使用一个标记是不是质数,是质数就标记为1,将不是质数的标记为0。
public int countPrimes(int n) {int [] isPrim = new int [n];int ans = 0;Arrays.fill(isPrim,1);for(int i =2;i<n;i++){if(isPrim[i] == 1){ans+=1;if(i*i<n){for(int j=i;j<n;j+=i){isPrim[j] = 0;}}}}return ans;
}
4. 丑数
定义:因数只包含2,3,5。当 n>0 时,若 n 是丑数,则 n 可以写成 n = 2 ^ a + 3 ^ b + 5 ^ c 的形式,其中 a,b,c 都是非负整数。特别地,当 a,b,c 都是 000 时,n=1。
4.1 丑数
丑数
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:n = 6
输出:true
解释:6 = 2 × 3
示例 2:
输入:n = 1
输出:true
解释:1 没有质因数,因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3:
输入:n = 14
输出:false
解释:14 不是丑数,因为它包含了另外一个质因数 7 。
4.2 数学法
public boolean isUgly(int n) {if(n<=0) return false;int [] factors = {2,3,5};for(int factor:factors){while(n % factor == 0){n /= factor;}}return n==1;}
相关文章:

算法通关村——数论经典问题解析
1. 辗转相除法 主要目的是获取两个数里面的最大公约数。 public int gcd(int a, int b) {int k 0;do {k a % b;a b;b k;} while (k ! 0);return a;}2. 素数和合数 素数的要求是必须大于等于2,并且只能被1和它本身整除。 判断的方法比较简单,就是从…...

代码随想录算法训练营第四十六天|LeetCode 1143,1035,53
目录 LeetCode 1143.最长公共子序列 动态规划五步曲: 1.确定dp[i][j]的含义 2.找出递推公式 3.初始化dp数组 4.确定遍历顺序 5.打印dp数组 LeetCode 1035.不相交的线 LeetCode 53.最大子序列和(动态规划) 动态规划五步曲: 1.确定…...

leetcode 541.反转字符串II
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/reverse-string-ii/ ps: 这道题描述的有点晦涩难懂,意思就是每隔k个反转k个,末尾不够k个时全部反转,开始就不够k个也全部反转。 代码&#…...

MyBatis与Spring整合以及AOP和PageHelper分页插件整合
目录 前言 一、MyBatis与Spring整合的好处以及两者之间的关系 1.好处 2.关系 二、MyBatis和Spring集成 1.导入pom.xml 2.编写配置文件 3.利用mybatis逆向工程生成模型层代码 三、常用注解 四、AOP整合pageHelper分页插件 创建一个切面 测试 前言 MyBatis是一个开源的…...

《认知觉醒》读书笔记之潜意识
模糊--人生是一场消除模糊的比赛。 学习知识,消除认知模糊 掌握的工具越多,认知能力越强,消除模糊的能力就越强。 元认知-----》 如何反观自己。 刻意练习----》 如何精进自己。 运动改造大脑---》 如何激化自己的运动热情。 学习知识的…...

Stable Diffusion 系列教程 | 图生图基础
前段时间有一个风靡全网的真人转漫画风格,受到了大家的喜欢 而在SD里,就可以通过图生图来实现类似的效果 当然图生图还有更好玩的应用,我们一点一点来探索 首先我们来简单进行一下图生图的这一个实践---真人转动漫 1. 图生图基本界面 和…...
cuda编程day001
一、环境: ①、linux cuda-11.3 opecv4.8.0 不知道头文件和库文件路径,用命令查找: # find /usr/local -name cuda.h 2>/dev/null # 查询cuda头文件路径 /usr/local/cuda-11.3/targets/x86_64-linux/include/cuda.h # find /usr/…...
Java 中使用 ES 高级客户端库 RestHighLevelClient 清理百万级规模历史数据
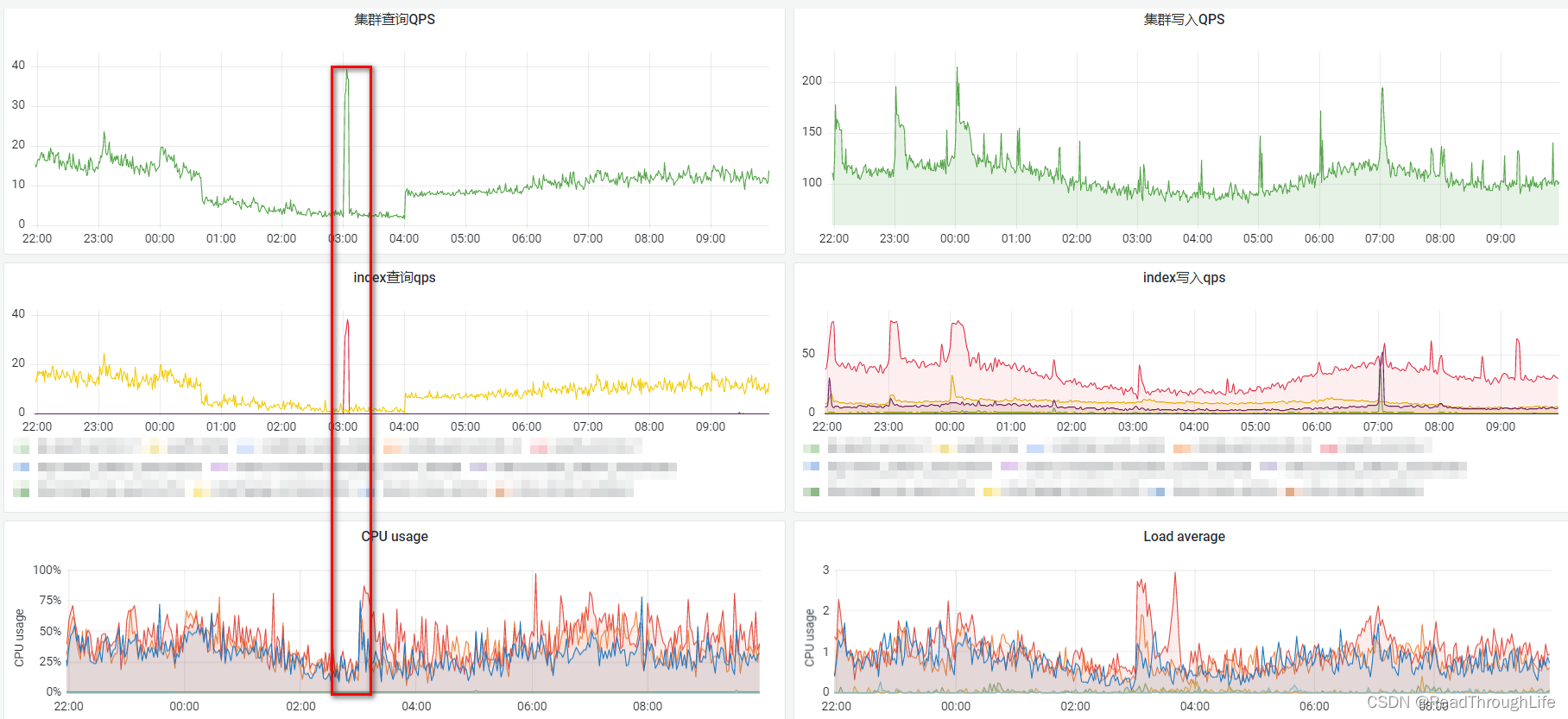
🎉工作中遇到这样一个需求场景:由于ES数据库中历史数据过多,占用太多的磁盘空间,需要定期地进行清理,在一定程度上可以释放磁盘空间,减轻磁盘空间压力。 🎈在经过调研之后发现,某服务…...
梯度下降230821a)
C++最易读手撸神经网络两隐藏层(任意Nodes每层)梯度下降230821a
// c神经网络手撸20梯度下降22_230820a.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 #include<iostream> #include<vector> #include<iomanip> // setprecision #include<sstream> // getline stof() #include<fstream…...

Leetcode 2235.两整数相加
一、两整数相加 给你两个整数 num1 和 num2,返回这两个整数的和。 示例 1: 输入:num1 12, num2 5 输出:17 解释:num1 是 12,num2 是 5 ,它们的和是 12 5 17 ,因此返回 17 。示例…...
Postman —— postman实现参数化
什么时候会用到参数化 比如:一个模块要用多组不同数据进行测试 验证业务的正确性 Login模块:正确的用户名,密码 成功;错误的用户名,正确的密码 失败 postman实现参数化 在实际的接口测试中,部分参数每…...
LeetCode--HOT100题(41)
目录 题目描述:102. 二叉树的层序遍历(中等)题目接口解题思路代码 PS: 题目描述:102. 二叉树的层序遍历(中等) 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地&am…...
)
微信小程序教学系列(6)
第六章:小程序商业化 第一节:小程序的商业模式 在这一节中,我们将探讨微信小程序的商业模式,让你了解如何将你的小程序变成一个赚钱的机器! 1. 广告收入 小程序的商业模式之一是通过广告收入赚钱。你可以在小程序中…...
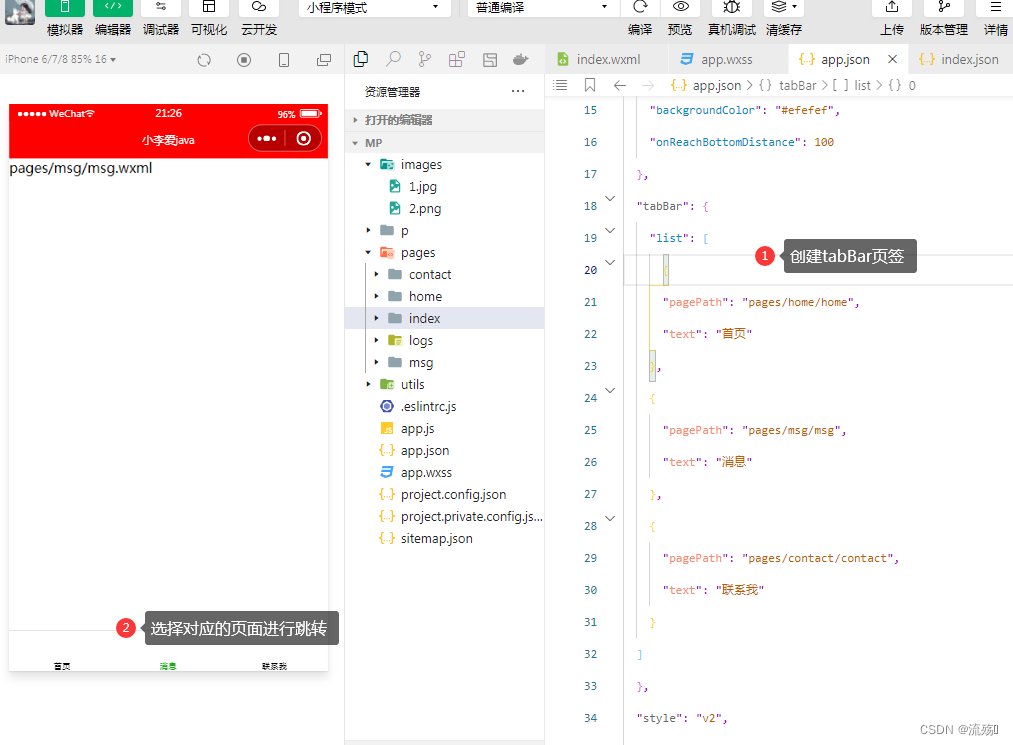
小程序中的全局配置以及常用的配置项(window,tabBar)
全局配置文件和常用的配置项 app.json: pages:是一个数组,用于记录当前小程序所有页面的存放路径,可以通过它来创建页面 window:全局设置小程序窗口的外观(导航栏,背景,页面的主体) tabBar:设置小程序底部的 tabBar效果 style:是否…...
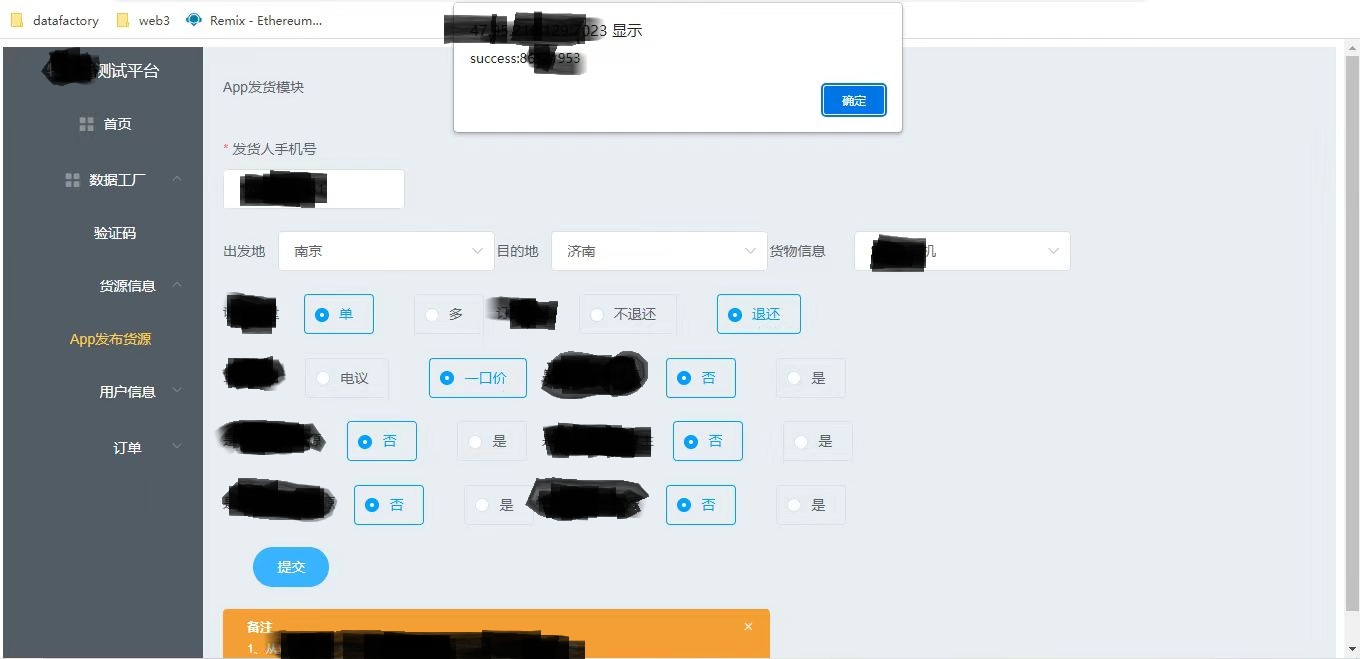
数据工厂调研及结果展示
数据工厂 一、背景 在开发自测、测试迭代测试、产品验收的过程中,都需要各种各样的前置数据,大致分为如下几类: 账号(实名、权益等级、注册等) 货源(优货、急走、相似、一手、普通货源等) …...
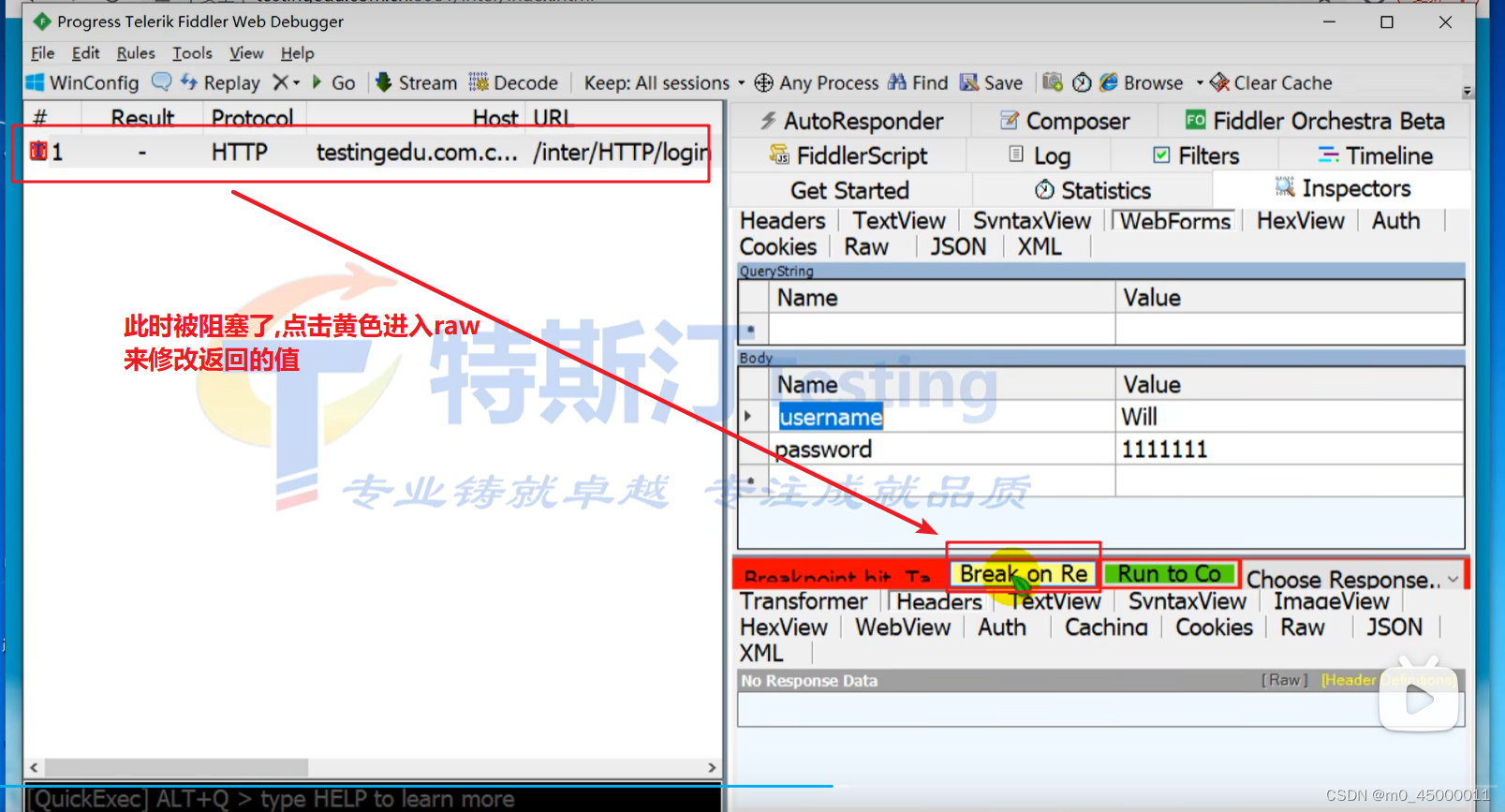
抓包相关,抓包学习
检查网络流量 - 提琴手经典 (telerik.com) Headers Reference - Fiddler Classic (telerik.com) 以上是fiddler官方文档 F12要勾选保留日志 不勾选的话跳转到新页面之前页面的日志不会在下方显示 会保留所有抓到的包 如果重定向到别的页面 F12抓包可能看不到响应信息,但是…...
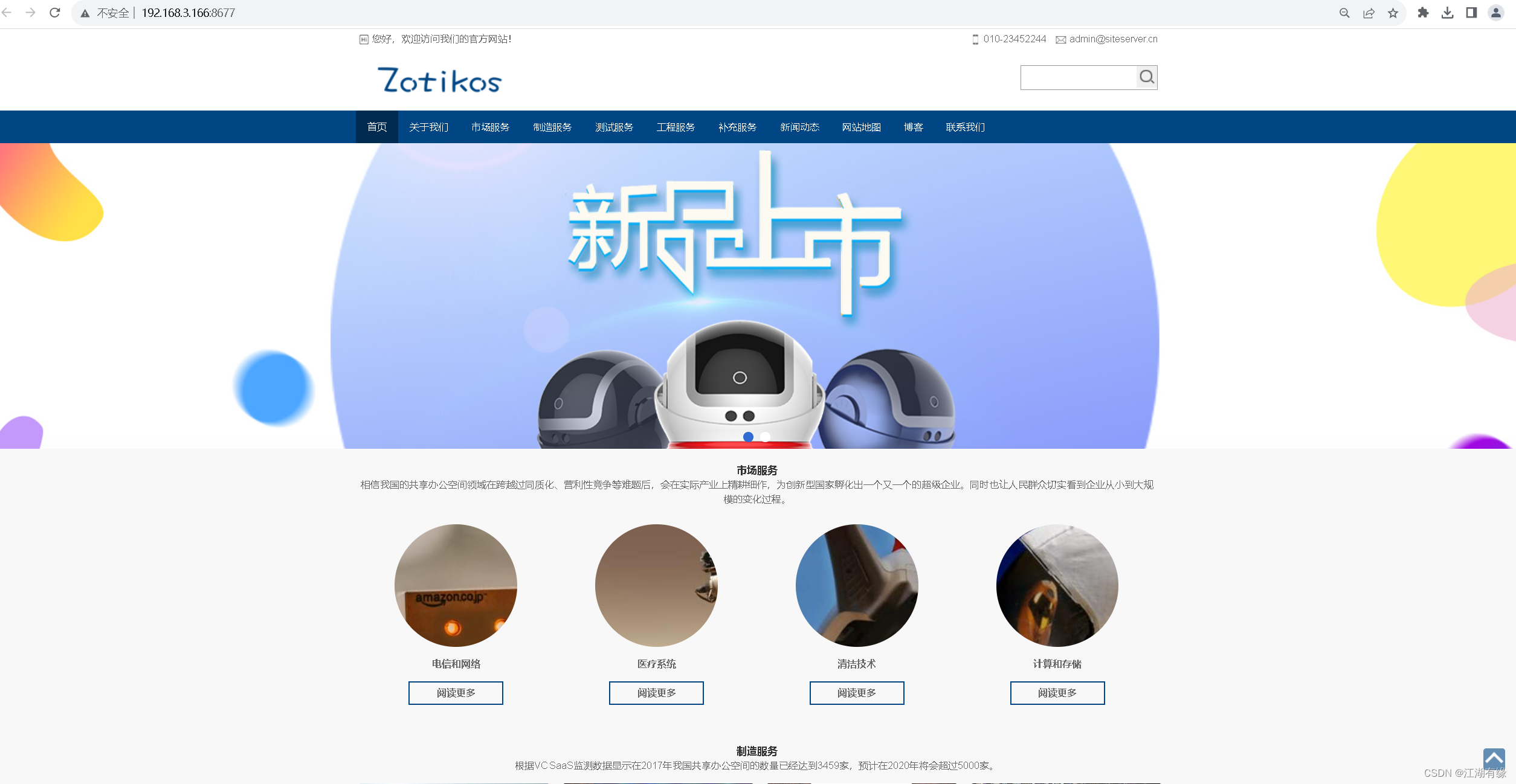
云原生之使用Docker部署SSCMS内容管理系统
云原生之使用Docker部署SSCMS内容管理系统 一、SSCMS介绍二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载SSCMS镜像五、部署SSCMS内容管理系统5.1 创建SSCMS容器5.2 检查SSC…...

uniapp -- 在组件中拿到pages.json下pages设置navigationBarTitleText这个值?
1:在 pages.json 文件中设置 navigationBarTitleText,例如: {"pages": [{"path": "pages/home/index","style": {"navigationBarTitleText": "首页",&...
Java获取环境变量和运行时环境信息和自定义配置信息
System.getenv() 获取系统环境变量 public static void main1() {Map<String, String> envMap System.getenv();envMap.entrySet().forEach(x-> System.out.println(x.getKey() "" x.getValue())); } System.getenv() 获取的是操作系统环境变量列表&…...
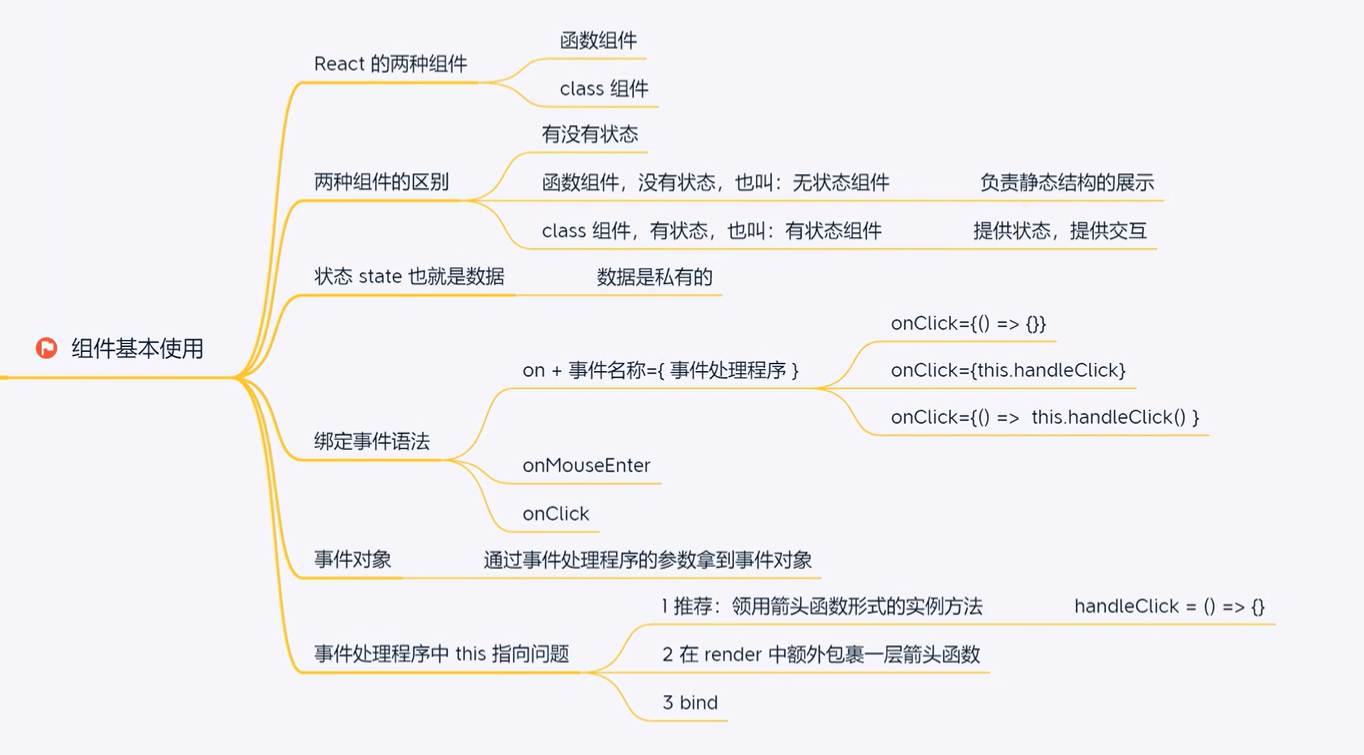
React入门 组件学习笔记
项目页面以组件形式层层搭起来,组件提高复用性,可维护性 目录 一、函数组件 二、类组件 三、 组件的事件绑定 四、获取事件对象 五、事件绑定传递额外参数 六、组件状态 初始化状态 读取状态 修改状态 七、组件-状态修改counter案例 八、this问…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
