【LeetCode】No.225. 用队列实现栈 -- Java Version
题目链接:https://leetcode.cn/problems/implement-stack-using-queues/
1. 题目介绍(225. 用队列实现栈)
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
- 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
- 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
【测试用例】:
示例:
输入:
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
【条件约束】:
提示:
- 1 <= x <= 9
- 最多调用100 次 push、pop、top 和 empty
- 每次调用 pop 和 top 都保证栈不为空
【跟踪】:
进阶:你能否仅用一个队列来实现栈。
2. 题解
2.1 两个队列实现栈 – O(n)
时间复杂度O(n),空间复杂度O(n)
class MyStack {// 1. 定义两个队列对象private Queue<Integer> queue1;private Queue<Integer> queue2;// 2. 定义一个变量,用于记录当前的queue元素长度private int curSize = 0;// 3. 构造方法,创建队列对象public MyStack() {queue1 = new LinkedList<>();queue2 = new LinkedList<>();}// 4. 入栈方法,如果哪个队列有值先添加到哪个,默认添加queue1public void push(int x) {if (!queue1.isEmpty()) queue1.offer(x);else if (!queue2.isEmpty()) queue2.offer(x);else queue1.offer(x);}// 5. 出栈方法public int pop() {// 判空if (empty()) return -1;// 至少有一个非空// 当queue1非空时,将queue1中size-1的元素出队存入queue2// 循环结束,queue1中只剩下一个元素,即栈顶元素(最后添加的元素)if (!queue1.isEmpty()){curSize = queue1.size();for (int i = 0; i < curSize-1; i++){queue2.offer(queue1.poll());}return queue1.poll();// queue1为空,说明queue2非空,步骤基本同上}else {curSize = queue2.size();for (int i = 0; i < curSize-1; i++){queue1.offer(queue2.poll());}return queue2.poll();}}// 6. 返回栈顶方法public int top() {// 定义一个临时值变量,用于记录queue出队值int ret = -1;// 判空if (empty()) return -1;// 至少有一个非空// 当queue1非空时,将queue1中所有的元素出队存入queue2// 同时通过临时值变量ret记录出队值,循环结束返回ret,即为栈顶元素if (!queue1.isEmpty()){curSize = queue1.size();for (int i = 0; i < curSize; i++){//System.out.println(queue1.size());ret = queue1.poll(); queue2.offer(ret);}System.out.println(ret);return ret;// queue1为空,说明queue2非空,步骤基本同上}else {curSize = queue2.size();for (int i = 0; i < curSize; i++){ret = queue2.poll(); queue1.offer(ret);}return ret;}}// 判空方法,queue1与queue2全为空,则为空public boolean empty() {return queue1.isEmpty() && queue2.isEmpty();}
}/*** Your MyStack object will be instantiated and called as such:* MyStack obj = new MyStack();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.top();* boolean param_4 = obj.empty();*/

改进:(官方题解)
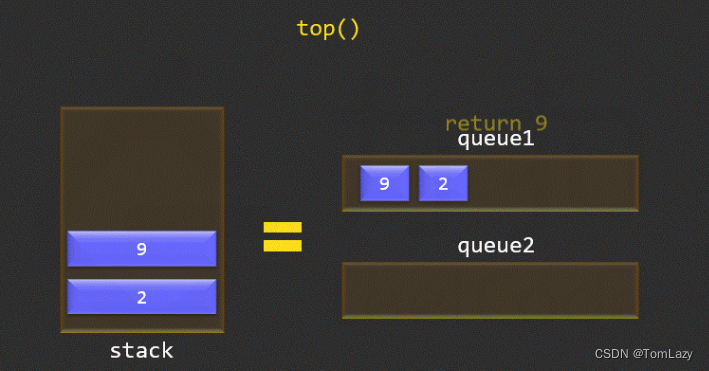
这里的改进点在于:push方法的巧妙设置,数据首先会存入queue2,并检查queue1是否为空,如果不为空,则将queue1中的元素全部出队,并存入queue2;然后借助临时变量交换queue1和queue2,保证每次push方法后,queue2始终为空,queue1为真正的栈结构,做到后进先出。
class MyStack {Queue<Integer> queue1;Queue<Integer> queue2;/** Initialize your data structure here. */public MyStack() {queue1 = new LinkedList<Integer>();queue2 = new LinkedList<Integer>();}/** Push element x onto stack. */public void push(int x) {queue2.offer(x);while (!queue1.isEmpty()) {queue2.offer(queue1.poll());}Queue<Integer> temp = queue1;queue1 = queue2;queue2 = temp;}/** Removes the element on top of the stack and returns that element. */public int pop() {return queue1.poll();}/** Get the top element. */public int top() {return queue1.peek();}/** Returns whether the stack is empty. */public boolean empty() {return queue1.isEmpty();}
}2.2 一个队列实现栈 – O(n)
时间复杂度O(n),空间复杂度O(n)
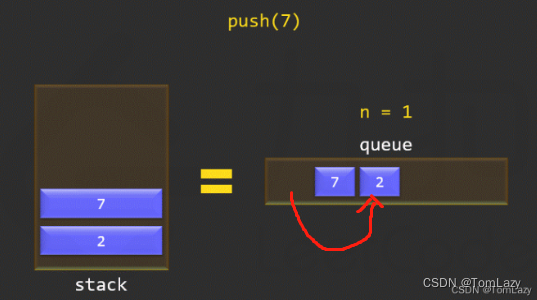
核心方法:当有新元素加入时,将原来的元素依次出队并重新入队,让队列中的元素始终保持倒序的状态。
class MyStack {Queue<Integer> queue;/** Initialize your data structure here. */public MyStack() {queue = new LinkedList<Integer>();}/** Push element x onto stack. */public void push(int x) {int n = queue.size();queue.offer(x);for (int i = 0; i < n; i++) {queue.offer(queue.poll());}}/** Removes the element on top of the stack and returns that element. */public int pop() {return queue.poll();}/** Get the top element. */public int top() {return queue.peek();}/** Returns whether the stack is empty. */public boolean empty() {return queue.isEmpty();}
}

3. 参考资料
[1] 用队列实现栈(官方题解)-- 部分代码来源
[2] 【LeetCode】No.232. 用栈实现队列 – Java Version(相似题目)
[3] 【LeetCode】剑指 Offer 09. 用两个栈实现队列 p68 – Java Version(相似题目)
相关文章:

【LeetCode】No.225. 用队列实现栈 -- Java Version
题目链接:https://leetcode.cn/problems/implement-stack-using-queues/ 1. 题目介绍(225. 用队列实现栈) 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、t…...
45个写规范代码的小技巧
目录 1、规范命名 2、规范代码格式 3、写好代码注释 4、try catch 内部代码抽成一个方法 5、方法别太长 6、抽取重复代码 7、多用return 8、if条件表达式不要太复杂 9、优雅地参数校验 10、统一返回值 11、统一异常处理 12、尽量不传递null值 13、尽量不返回null值…...
MindFusion Diagramming for Java, 最新版 Crack
Diagramming for Java, V4.6.1 A unique Java Swing library for any type of flowchart.您需要的每一个图表功能 图表、方案、图形、网络、算法、树、图表 - 所有这些都是使用 MindFusion Diagramming for Java 工具快速轻松地构建的。结果令人着迷。 Java Dagram 库ÿ…...
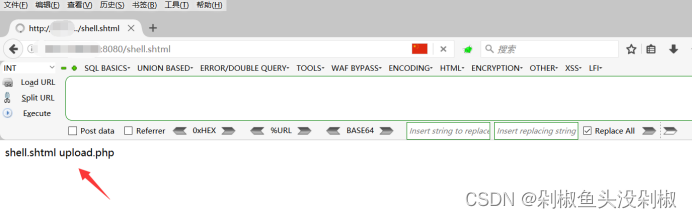
中间件安全—Apache常见漏洞
中间件安全—Apache常见漏洞1.Apache常见漏洞1.1.Apache介绍1.2.Apache HTTPD 换行解析漏洞(CVE-2017-15715)1.2.1.漏洞介绍1.2.2.漏洞环境1.2.2.1.运行漏洞环境1.2.2.2.访问漏洞环境1.2.3.漏洞复现1.2.3.1.拦截1.2.3.2.添加换行1.2.3.3.访问文件1.3.Apa…...
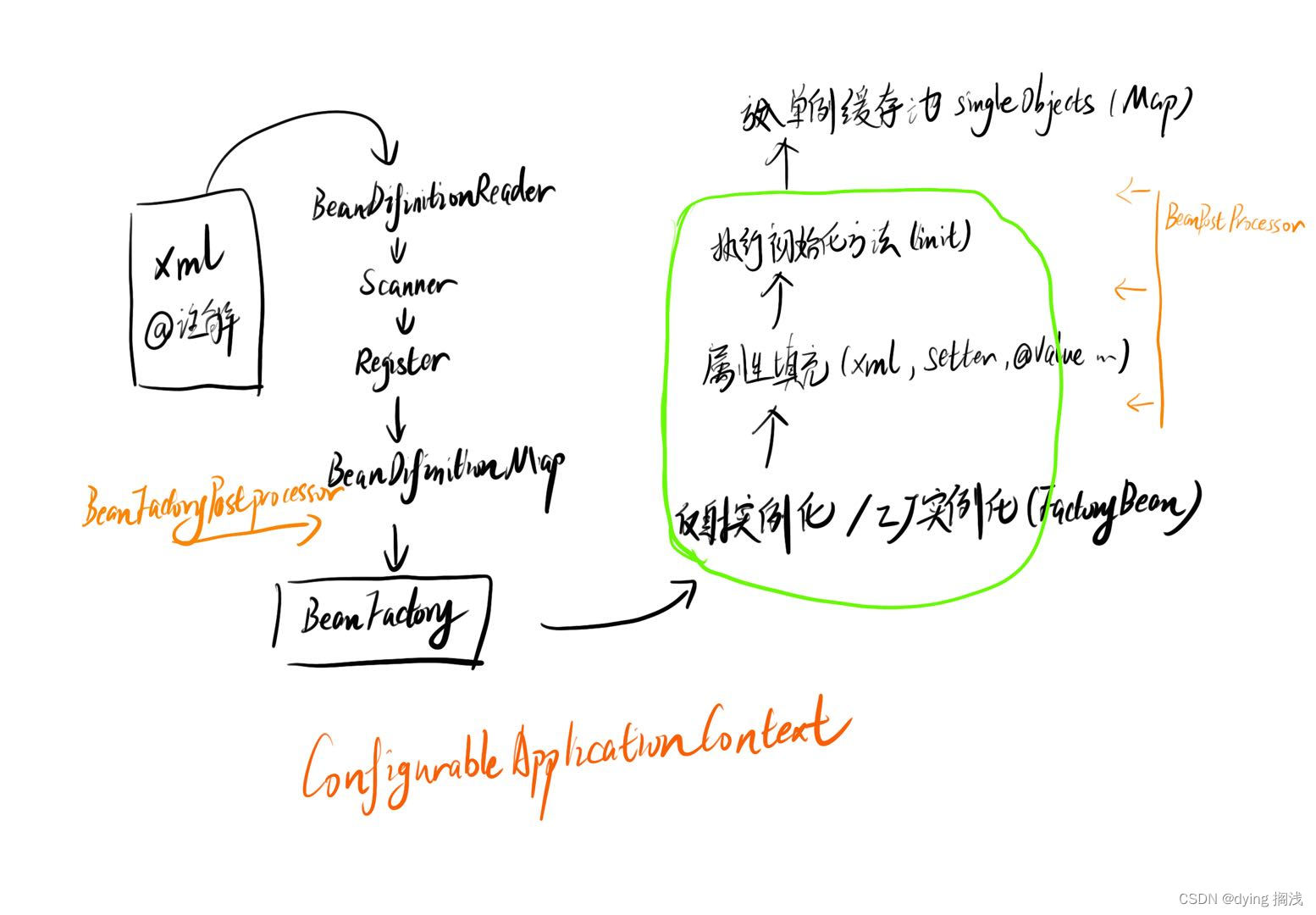
Spring IOC 容器 Bean 加载过程
Spring IOC 容器 Bean 加载过程 Spring 对于我们所有的类对象进行了统一抽象,抽象为 BeanDefinition ,即 Bean 的定义,其中定义了类的全限定类名、加载机制、初始化方式、作用域等信息,用于对我们要自动装配的类进行生成。 Sprin…...
)
【DRF】Django Rest Framework(5.DRF中的通用视图类-GenericAPIView方法说明与使用说明)
1. GenericAPIView [通用视图类],概述 继承自 APIView增加了操作序列化器和数据库查询的方法,作用是为下面Mixin扩展类的执行提供方法支持。通常在使用时,可搭配一个或者多个Mixin扩展类源码 当我们查看 GenericAPIView 的源码时,…...

STM32 OTA应用开发——自制BootLoader
STM32 OTA应用开发——自制BootLoader 目录STM32 OTA应用开发——自制BootLoader前言1 环境搭建2 BootLoader工作原理以及常见分区介绍3 BootLoader的制作4 烧录下载配置5 运行测试结束语前言 什么是OTA? 百度百科:空中下载技术(Over-the-Ai…...

时域和频域的简单理解
目录文章背景结论举例说明说回频域连续或离散总结文章背景 时域和频域在傅里叶变换和拉普拉斯变换,z变换中经常提到的高频词。本文的重点就是想说明怎么理解 “频域” 这个名词。 结论 频域就是一个信号 所有组成频率的取值范围的集合 举例说明 以大家从中小学开…...

华为OD机试 - 第 K 个最小码值的字母 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
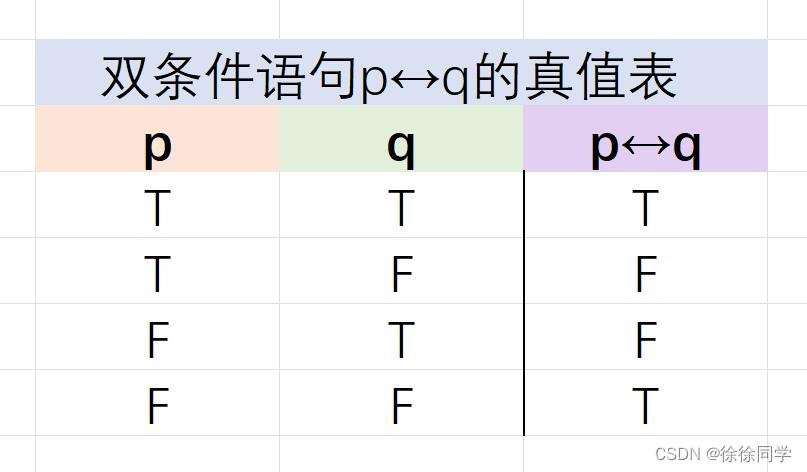
离散数学笔记_第一章:逻辑和证明(1)
1.1命题逻辑1.1.1 命题 1.1.2 逻辑运算符 定义1: 否定联结词定义2: 合取联结词定义3: 析取联结词定义4: 异或联结词1.1.3 条件语句 定义5: 条件语句定义6: 双条件语句1.1.1 命题 1.命题:是…...

Rust FFI 与C语言互相调用
参考 https://cloud.tencent.com/developer/article/2077534 https://github.com/shepmaster/rust-ffi-omnibus cbindgen 简介 二进制方式构建 $ cargo install cbindgen //默认构建C头文件 C语言需要 --lang C $ cd /path/to/my/project && cbindgen . -o target/…...

从全局变量寻找到Tomcat回显方式
前言 对于回显的获取主要是在ApplicationFilterChain类的lastServicedRequest / lastServicedResponse两个属性,是使用的ThreadLocal进行修饰的,并且,在执行请求的过程中,通过反射修改属性值,能够记录下当前线程的req…...

Tapdata Connector 实用指南:数据入仓场景之数据实时同步到 BigQuery
【前言】作为中国的 “Fivetran/Airbyte”, Tapdata 是一个以低延迟数据移动为核心优势构建的现代数据平台,内置 60 数据连接器,拥有稳定的实时采集和传输能力、秒级响应的数据实时计算能力、稳定易用的数据实时服务能力,以及低代码可视化操作…...

关于机器人状态估计(12)-VIO/VSLAM的稀疏与稠密
VIO三相性与世界观室内ALL IN ONE 首先以此链接先对近期工作的视频做个正经的引流,完成得这么好的效果,仅仅是因为知乎限流1分钟以内的视频,导致整个浏览量不到300,让人非常不爽。 这套系统已经完成了,很快将正式发布…...
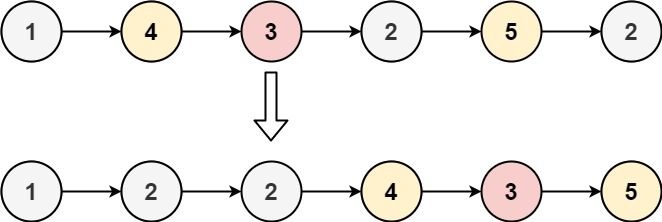
Python每日一练(20230220)
目录 1. 存在重复元素 II 2. 按要求实现程序功能 3. 分割链表 附录 链表 1. 存在重复元素 II 给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] nums [j],并且 i 和 j 的差的 绝对值 至多为 k。 …...

技术总监的“技术提升”
技术负责人的能力要求是什么?成本中心技术负责人最重要的工作是让其他CXO理解、认可并且支持技术部的工作,否则作为成本部门,在公司的地位会很低。技术创新光是让其他部门理解还不行,技术还需要创造价值,所以需要做技术创新。上面…...
kettle安装部署_简单认识_Spoon勺子界面---大数据之kettle工作笔记002
然后我们来看一下这个kettle的安装,很简单,下载解压就可以了 上面的地址是官网很烂 下面的地址好一些 这个是官网可以看到很慢,很不友好 这个是下面那个地址,可以看到 最新的是9.0了,一般都用 一般都用8.2 这里下载这个就可以了 下载以后可以看到有个pdi...
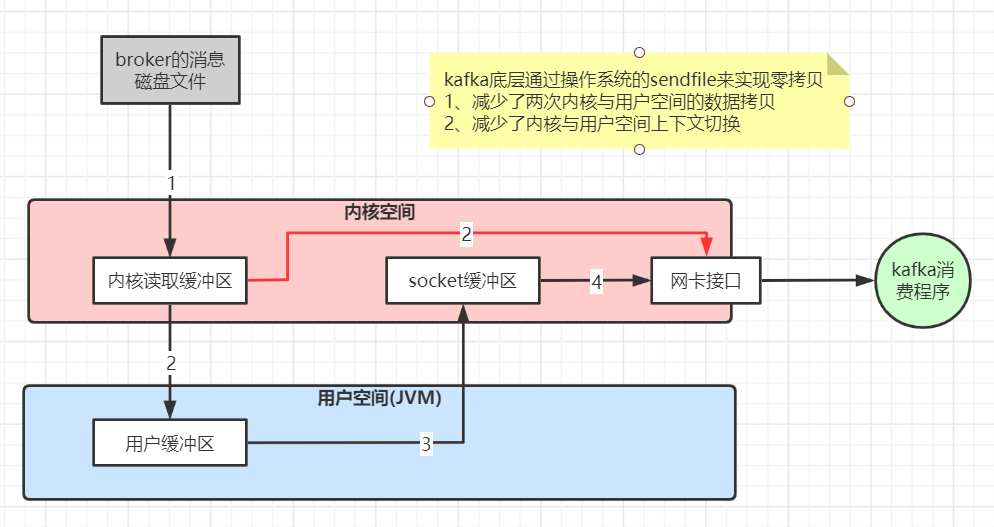
第三章 Kafka生产问题总结及性能优化实践
第三章 Kafka生产问题总结及性能优化实践 1、线上环境规划 JVM参数设置 kafka 是 scala 语言开发,运行在 JVM 上,需要对 JVM 参数合理设置,参看 JVM 调优专题 修改 bin/kafka-start-server.sh 中的 JVM 设置,假设机器是 32G 内…...

Comparable和Comparator的区别
一、概述 Comparable和Comparator都是用来实现比较的,一般用于集合中元素的比较 基本包装类型,Integer、Long以及String都实现了Comparable接口,该接口的排序逻辑必须写在比较对象中,所以又叫自然排序 我们一般集合排序使用的Col…...

全15万字丨PyTorch 深度学习实践、基础知识体系全集;忘记时,请时常回顾。
✨ ✨我们抬头便看到星光,星星却穿越了万年. ✨ ✨ 🎯作者主页:追光者♂ 🌸个人简介:在读计算机专业硕士研究生、CSDN-人工智能领域新星创作者🏆、2022年度博客之星人工智能领域TOP4🌟、阿里云…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
