算法修炼Day60|● 84.柱状图中最大的矩形
LeetCode:84.柱状图中最大的矩形
84. 柱状图中最大的矩形 - 力扣(LeetCode)
1.思路
双指针思路,以当前数组为中心,借助两个数组存放当前数柱左右两侧小于当前数柱高度的索引,进行h*w的计算。注意首尾节点的左侧索引和右侧索引需要单独声名为0.
单调栈,在原数组的基础上定义一个新的数组,对其进行首尾节点的扩容。思路延续收集雨水。
2.代码实现
class Solution {public int largestRectangleArea(int[] heights) { Stack<Integer> stack = new Stack<>(); // 数组扩容 int[] newHeights = new int[heights.length + 2]; newHeights[0] = 0; newHeights[newHeights.length - 1] = 0; for (int i = 0; i < heights.length; i++) { newHeights[i + 1] = heights[i]; } heights = newHeights; // 改变数组引用 stack.add(0); int result = 0; for (int i = 1; i < heights.length; i++) { if (heights[i] > heights[stack.peek()]) { // 入栈 stack.add(i); } else if (heights[i] == heights[stack.peek()]) { stack.pop(); // 弹出 stack.add(i); // 入栈 } else { while (heights[i] < heights[stack.peek()]) { int mid = stack.peek(); // 当前数值柱子 stack.pop(); int left = stack.peek(); int right = i; int w = right - left - 1; int h = heights[mid]; result = Math.max(result, w * h); } stack.add(i); } } return result;}}3.复杂度分析:
时间复杂度:O(n).
空间复杂度:O(n).符合单调递减的情况时,全部入栈。
相关文章:

算法修炼Day60|● 84.柱状图中最大的矩形
LeetCode:84.柱状图中最大的矩形 84. 柱状图中最大的矩形 - 力扣(LeetCode) 1.思路 双指针思路,以当前数组为中心,借助两个数组存放当前数柱左右两侧小于当前数柱高度的索引,进行h*w的计算。注意首尾节点的左侧索引…...
)
前端面试题css(一)
题目 盒子垂直水平居中如何实现text-align:center vertical-align: middle水平垂直居中布局positionmargin水平垂直居中布局 grid栅格化布局及其兼容性介绍一下BFC触发 BFC 的条件包括:常见的用途包括: 写过的动画效果overflow有哪些属性visible&#x…...

.NETCORE中关于swagger的分组
有些时候我们的项目接口过多,就希望对应的swagger能够执行分组,网络上的几乎是千篇一律的分组方法,会累死! 这里提供一个更加高效的分组方法,比如你可以说哪些模块分到哪个组,哪些权限分到哪个组ÿ…...

4.1011
目录 四次挥手中收到乱序的FIN包会如何处理? 在 TIME_WAIT 状态的 TCP 连接,收到 SYN 后会发生什么? 四次挥手中收到乱序的FIN包会如何处理? 如果FIN报文比数据包先道道客户端,此时FIN是一个乱序报文,此时…...

uniapp中引入axios的错误?
场景 在unaipp中使用axios npm i axios 下载完成后 然后在页面中使用 axios.get(“http://3000/searchS”) 然后报错 Adapter http’ is not available in the build 原因 在 UniApp 中使用 Axios 发送 HTTP 请求时,如果出现错误 “Adapter http’ is not available…...

Discuz!论坛发帖标题字数限制80字符可以修改吗?修改发帖标题字数的方法
Discuz!论坛发帖标题字数限制80字符修改方法 1.数据库修改2.修改JS验证字符数文件3.修改模板中写死的字符限制数4.修改函数验证文件5.修改语言包文件6.更新缓存 Discuz X3.4论坛网站帖子标题字数限制80字符,当我们想使用长标题的时候就得一删再删,实在是…...
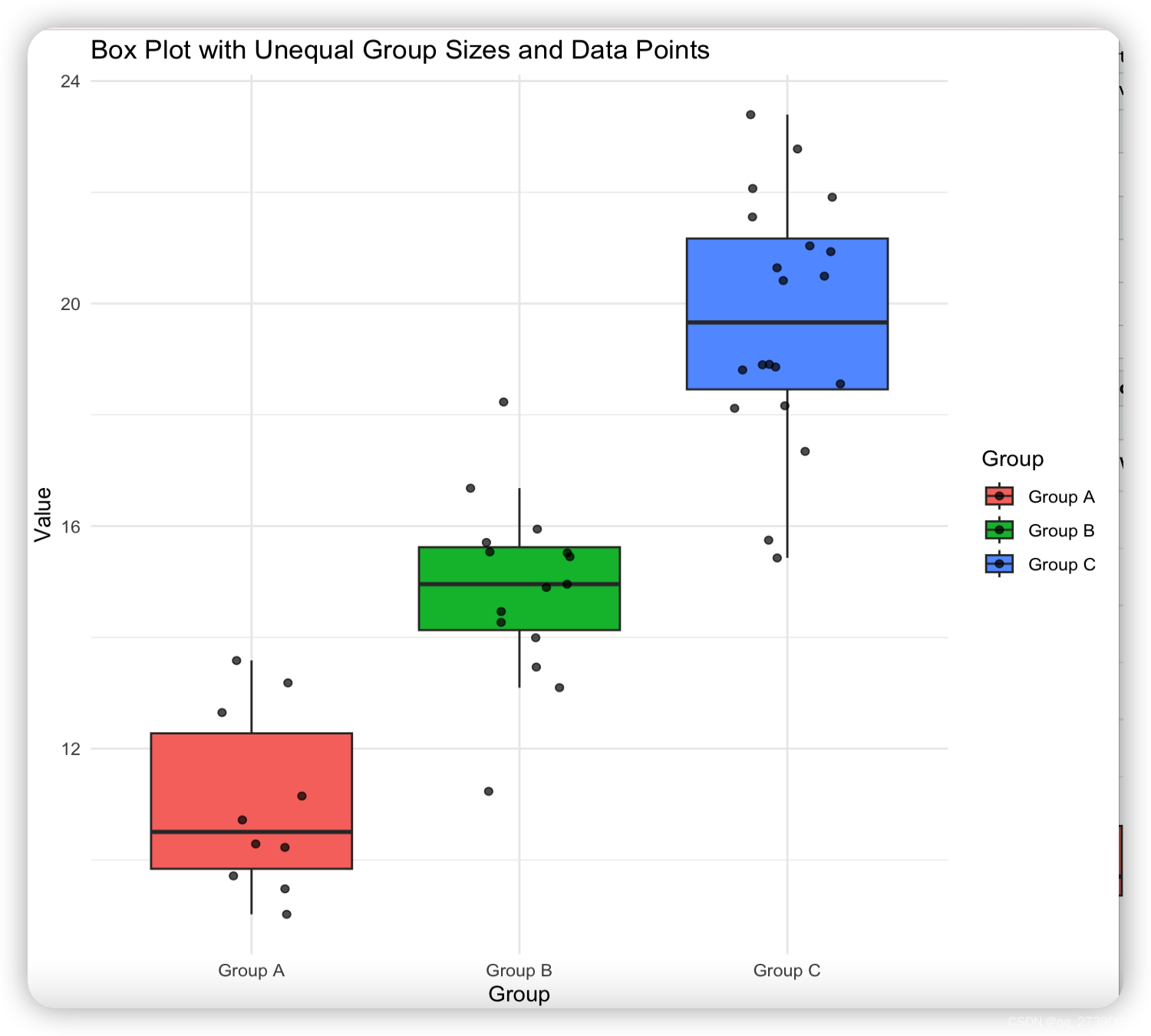
R语言画样本不均衡组的箱线图
# 导入 ggplot2 包 library(ggplot2)# 示例数据框,包含数值数据和分组信息 data <- data.frame(Group c(rep("Group A",10), rep("Group B",15),rep("Group C",20)),Value c(rnorm(10, mean 10, sd 2),rnorm(15, mean 15, sd…...
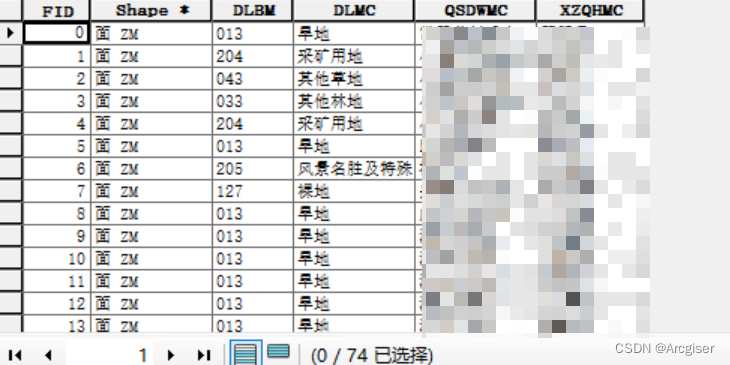
ArcGIS学习总结(19)——要素转点与空间连接(属性表字段映射)
1.在新创建的面矢量数据的属性表中没有对应的字段信息,为了能够和有属性信息的数据进行匹配,使其具有对应字段的信息。 2.需要匹配的矢量文件属性表信息。 3.对新创建的矢量文件执行要素转点:数据管理工具→要素→要素转点。 4.选择分析工…...

【每日一题Day306】LC228汇总区间 | 双指针
汇总区间【LC228】 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范…...
vue中实现echarts三维散点图
需要安装 echarts 同时引入 echarts-gl 我安装的版本: "echarts": "^5.3.2", "echarts-gl": "^2.0.9", import Vue from "vue"; import * as echarts from "echarts"; Vue.prototype.$echarts echa…...

多头自注意力机制的代码实现
文章目录 1、自注意力机制2、多头注意力机制 transformer的整体结构: 1、自注意力机制 自注意力机制如下: 计算过程: 代码如下: class ScaledDotProductAttention(nn.Module):def __init__(self, embed_dim, key_size, value_…...

抽象工厂模式
目录 了解抽象工厂模式前的前置知识 什么是抽象工厂模式? 为什么要提出抽象工厂模式? 抽象工厂模式中的四大角色? 抽象工厂模式的优缺点? 抽象工厂模式的适用场景? 了解抽象工厂模式前的前置知识 在讲抽象工厂模式…...
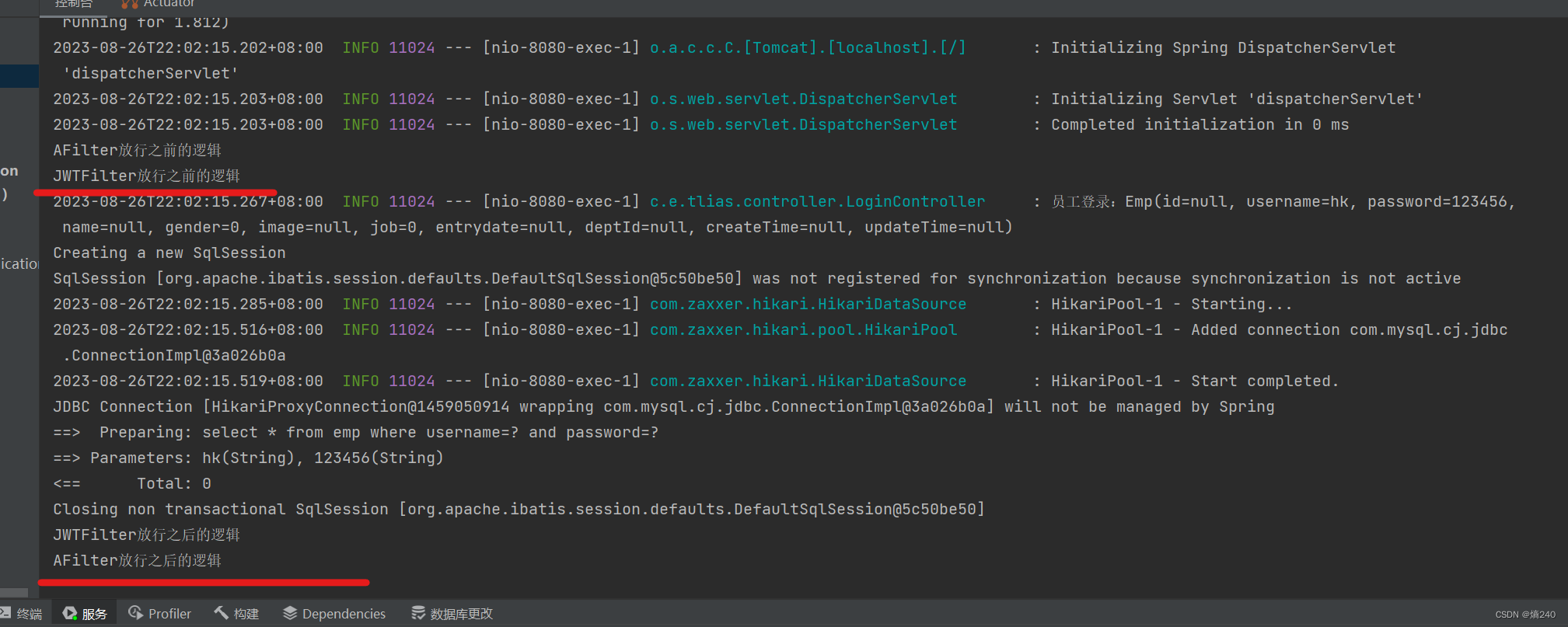
登录校验-Filter-详解
目录 执行流程 拦截路径 过滤器链 小结 执行流程 过滤器Filter拦截到请求之后,首先执行方放行之前的逻辑,然后执行放行操作(doFilter),然后会访问对应的Web资源(对应的Controller类)&#…...

堆栈方法区笔记记录
成员变量分两种: 1)实例变量:没有static修饰,属于对象,存储在堆中,有几个对象就有几份,通过对象点来访问 2)静态变量:由static修饰,属于类,存储在方法区中,只有一份,通过类名点来访…...

新版微信小程序获取用户手机号
小程序手机号验证组件有两种 手机号快速验证组件 //原生写法 <button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber"></button>Page({getPhoneNumber (e) {console.log(e.detail.code)} })uniapp写法 <button open-type…...

CSS实践 —— 悬浮盒子阴影加上移效果
悬浮盒子阴影加上移效果 代码 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>Title</title><style>body{background-color: #f5f5f5;}.shadow {width: 100px;height: 100px;margin:…...

安全测试基础知识
软件安全测试是评估和测试系统以发现系统及其数据的安全风险和漏洞的过程。没有通用术语,但出于我们的目的,我们将评估定义为分析和发现漏洞,而不尝试实际利用这些漏洞。我们将测试定义为发现和尝试利用漏洞。 安全测试通常根据要测试的漏洞…...

列表首屏毫秒级加载与自动滚动定位方案
引用自 摸鱼wiki 场景 <template><div ref"commentsRef"><divv-for"comment in displayComments":key"comment.id":data-cell-id"comment.id"class"card">{{ comment.data }}</div></div> &…...

小区物业业主管理信息系统设计的设计与实现(论文+源码)_kaic
摘 要 随着互联网的发展,网络技术的发展变得极其重要,所以依靠计算机处理业务成为了一种社会普遍的现状。管理方式也自然而然的向着现代化技术方向而改变,所以纯人工管理方式在越来越完善的现代化管理技术的比较之下也就显得过于繁琐&#x…...
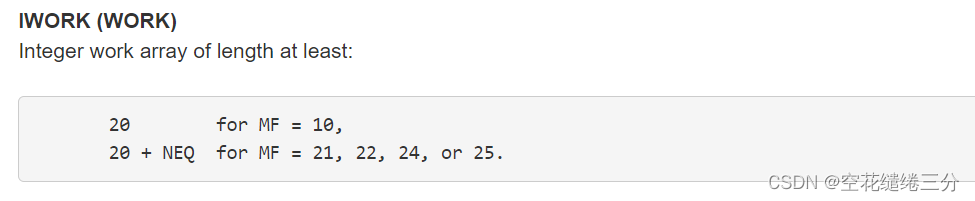
Fortran 微分方程求解 --ODEPACK
最近涉及到使用Fortran对微分方程求解,我们知道MATLAB已有内置的函数,比如ode家族,ode15s,对应着不同的求解办法。通过查看odepack的官方文档,我尝试使用了dlsode求解刚性和非刚性常微分方程组。 首先是github网址&am…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
