从零学算法 (剑指 Offer 13)
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
原题链接
- 我的思路:从左上角 [0,0] 开始 dfs,如果行列坐标的数位之和大于 k 就返回 0,如果来过了这个点也返回 0,如果超出边界了也返回 0,否则就算是一个能够到达的格子,返回 1+dfs(往右走)+dfs(往下走)。因为是从左上角开始,所以往右和往下足以遍历每个格子。
-
int M,N,K;Set<Integer> set = new HashSet<>();public int movingCount(int m, int n, int k) {M=m;N=n;K=k;return dfs(0,0);}public int dfs(int x,int y){// 超出边界if(x>=M || y>=N)return 0;// 不符题意if(getNum(x,y)>K)return 0;// 已计算过if(set.contains(x*N+y))return 0;set.add(x*N+y);int ans = dfs(x+1,y)+dfs(x,y+1)+1;return ans;}// 获取格子行列数位和public int getNum(int x,int y){int ans = 0;while(x>0){ans+=x%10;x/=10;}while(y>0){ans+=y%10;y/=10;}return ans;} - 他人题解:获取格子行列数位和这部分可以优化,以下用 sum 代替一个数的数位和 。一个数在递增的时候,只要没满十,规律都是
sum(x)=sum(x-1)+1,比如 16 和 17 和 18 的 sum 就是 7->8->9。如果满十进一了,就相当于把原本的 9 变成了 0,之前的一位加了 1,算下来就是减少了 8,所以此时 sum(x) = sum(x-1)-8,总结一下就是sum(x) = x%10==0?s(x-1)-8:sum(x-1)+1。也就是说一个坐标的行列在变化时,他的数位和就能根据这个规律来计算,所以在 dfs 的入参中加入坐标 [i,j] 对应的 sum(i) 和 sum(j),就能递推得到一个坐标的数位和。 -
int m,n,k;// 用数组判断是否来过某个点更快boolean[][] see;public int movingCount(int m, int n, int k) {this.m=m;this.n=n;this.k=k;this.see = new boolean[m][n];return dfs(0,0,0,0);}public int dfs(int x,int y,int sx,int sy){if(x>=m || y>=n || sx+sy>k || see[x][y])return 0;see[x][y]=true;int newSx = (x+1)%10==0?sx-8:sx+1;int newSy = (y+1)%10==0?sy-8:sy+1;int ans = dfs(x+1,y,newSx,sy)+dfs(x,y+1,sx,newSy)+1;return ans;} - 他人题解2:既然是遍历每个格子,那其实 bfs 也行,原理都一样,就不赘述了
-
public int movingCount(int m, int n, int k) {boolean[][] visited = new boolean[m][n];int res = 0;Queue<int[]> queue= new LinkedList<int[]>();// 熟悉的 dfs 入参,坐标以及坐标对应的 sumqueue.add(new int[] { 0, 0, 0, 0 });while(queue.size() > 0) {int[] x = queue.poll();int i = x[0], j = x[1], si = x[2], sj = x[3];// 相当于 dfs 的 return 0if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;visited[i][j] = true;// 以下三行相当于 return dfs(下)+dfs(右)+1res ++;queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });}return res;}
相关文章:
)
从零学算法 (剑指 Offer 13)
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如&am…...

854之数据结构
一.线性表 1.顺序表 #include <iostream> #include<stdlib.h> using namespace std; #define max 100 typedef struct {int element[max];int last; } List; typedef int position ; void Insert(int x, position p, List &L) {position q;if (L.last > ma…...
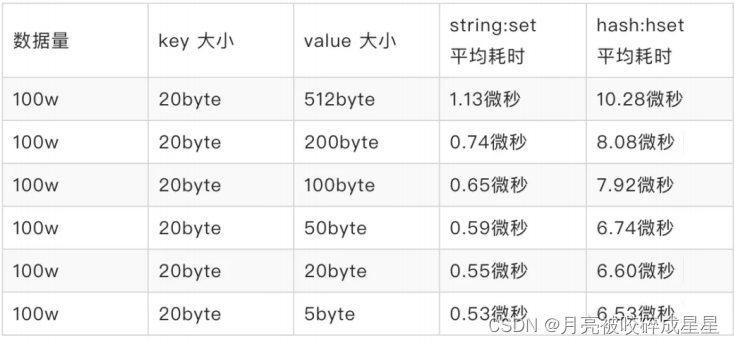
Redis从基础到进阶篇(二)----内存模型与内存优化
目录 一、缓存通识 1.1 ⽆处不在的缓存 1.2 多级缓存 (重点) 二、Redis简介 2.1 什么是Redis 2.2 Redis的应用场景 三、Redis数据存储的细节 3.1 Redis数据类型 3.2 内存结构 3.3 内存分配器 3.4 redisObject 3.4.1 type 3.4.2 encoding 3…...
DBO优化SVM的电力负荷预测,附MATLAB代码
今天为大家带来一期基于DBO-SVM的电力负荷预测。 原理详解 文章对支持向量机(SVM)的两个参数进行优化,分别是:惩罚系数c和 gamma。 其中,惩罚系数c表示对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。c越小࿰…...

第一百二十五回 dart中List和Map的常见用法
文章目录 概念介绍使用方法初始化相互转换元素操作 经验分享 我们在上一章回中介绍了Flexible组件相关的内容,本章回中将介绍 dart中的List和Map.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里介绍的List也叫列表,它表示一组相…...
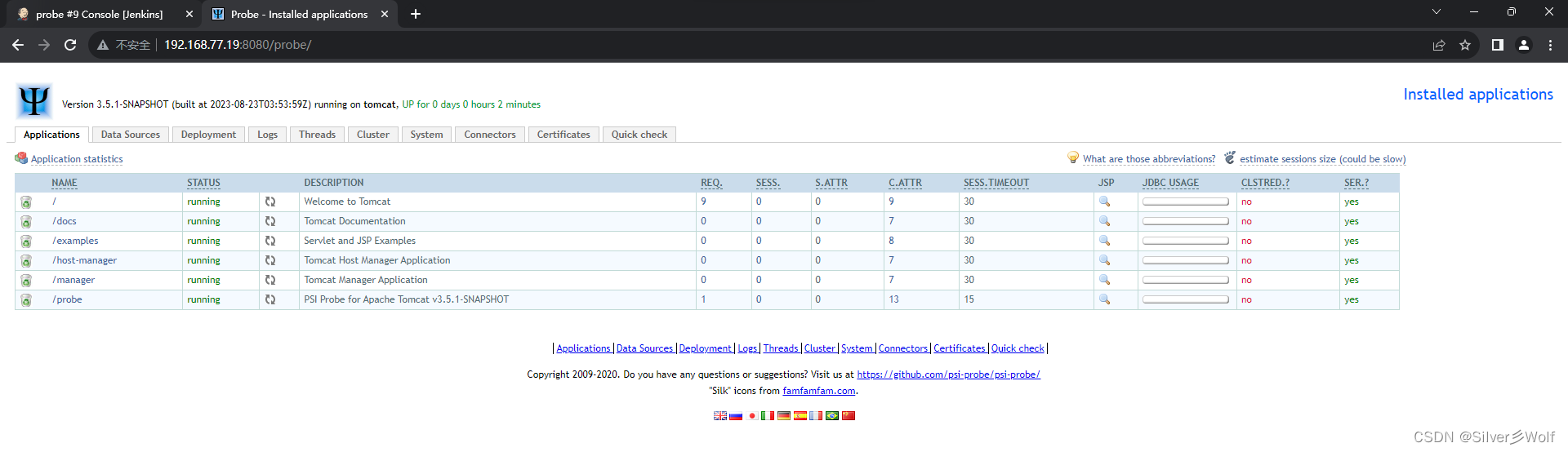
小白到运维工程师自学之路 第七十九集 (基于Jenkins自动打包并部署Tomcat环境)2
紧接上文 4、新建Maven项目 clean package -Dmaven.test.skiptrue 用于构建项目并跳过执行测试 拉到最后选择构建后操作 SSH server webExec command scp 192.168.77.18:/root/.jenkins/workspace/probe/psi-probe-web/target/probe.war /usr/local/tomcat/webapps/ /usr/loca…...
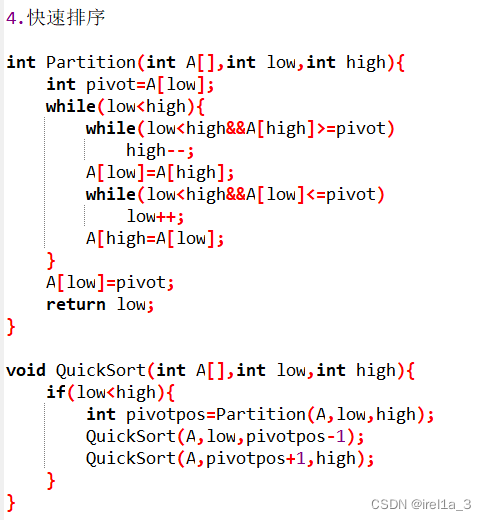
林【2021】
三、应用 1.字符串abaaabaabaa,用KMP改进算法求出next和nextval的值 2.三元组矩阵 4.二叉树变森林 四、代码(单链表递增排序,二叉树查找x,快速排序)...
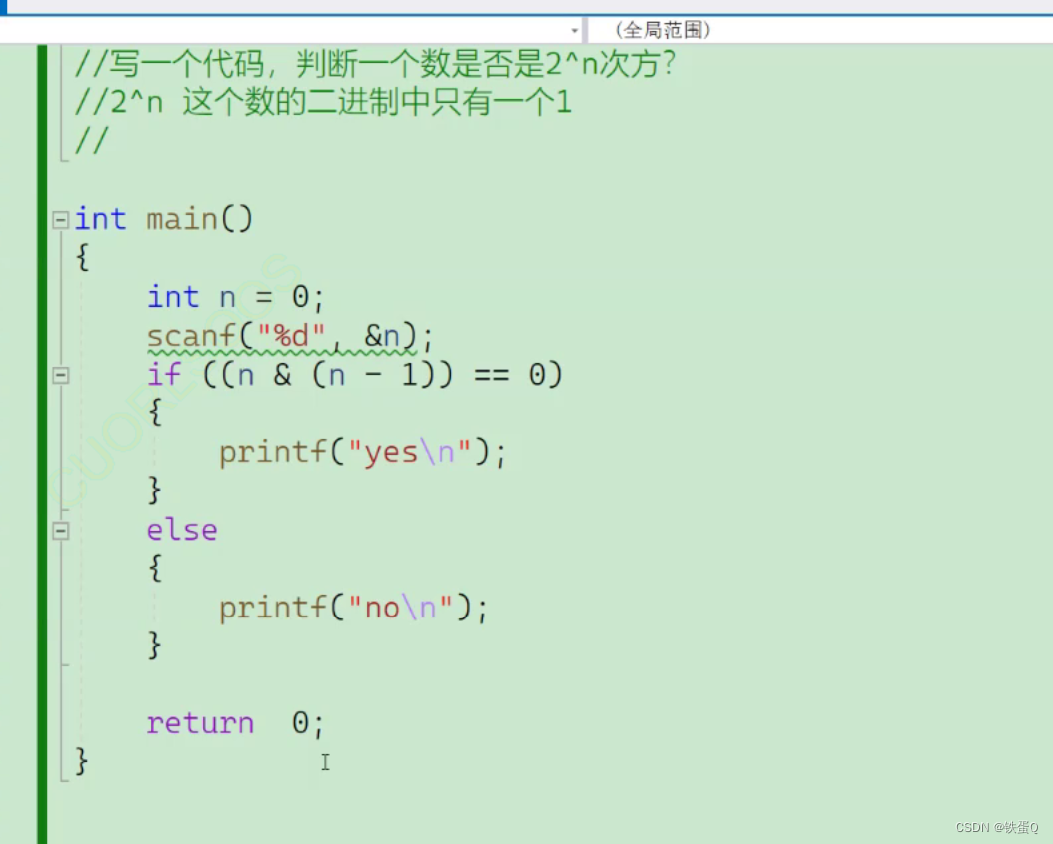
c语言练习题30:判断一个数是否为2^n
判断一个数是否为2^n 思路:2^n中只有一个1故可以通过n&(n-1)是否为0来判断。 代码:...

VX小程序 实现区域转图片预览
图例 方法一 1、安装插件 wxml2canvas npm install --save wxml2canvas git地址参照:https://github.com/wg-front/wxml2canvas 2、类型 // 小程序页面 let data{list:[{type:wxml,class:.test_center .draw_canvas,limit:.test_center,x:0,y:0}] } 3、数据结…...
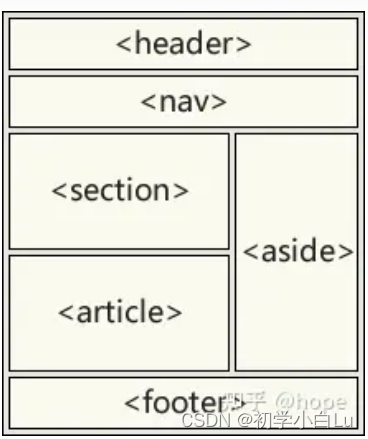
HTML5-1-标签及属性
文章目录 语法规范标签规范标签列表通用属性基本布局 页面的组成: HTML(HyperText Markup Language,超文本标记语言)是用来描述网页的一种语言,它不是一种编程语言,而是一种标记语言。 HTML5 是下一代 HTM…...

5017. 垦田计划
Powered by:NEFU AB-IN Link 文章目录 5017. 垦田计划题意思路代码 5017. 垦田计划 题意 略 思路 二分最小需要几天即可 注意: 天数不能低于k二分时,若耗时天数小于mid,直接continue 代码 /* * Author: NEFU AB-IN * Date: 2023-08-26 22:4…...

【校招VIP】产品思维分析之面试新的功能点设计
考点介绍: 这种题型是面试里出现频度最高,也是难度最大的一种,需要面试者对产品本身的功能、扩展性以及行业都有一定的了解。而且分析时间较短,需要一定的产品能力和回答技巧。 『产品思维分析之面试新的功能点设计』相关题目及解…...

indexDB vue 创建数据库 创建表 添加对象数据
1 .open(dbName,1) 版本号可以省略 let dbName hist-data-1dconst request indexedDB.open(dbName); // 如果你不知道数据库的版本号,可以省略第二个参数,这样 indexedDB 会默认为你打开最新版本的数据库,因为版本号总是自增长的 2 第一次…...
Django基础1——项目实现流程
文章目录 一、前提了解二、准备开发环境2.1 创建项目2.1.1 pycharm创建2.1.2 命令创建 2.2 创建应用 例1:效果实现例2:网页展示日志文件 一、前提了解 基本了解: 官网Django是Python的一个主流Web框架,提供一站式解决方案…...

基于SSM的在线购物系统——LW模板
摘 要 人类进入21世纪以来,很多技术对社会产生了重大的影响。信息技术是最具代表的新时代技术,信息技术起源于上世纪,在起初的时候只是实现在单机上进行信息的数字化管理,随着网络技术、软件开发技术、通讯技术的发展,…...

Mac操作系统上设置和配置PPPoE连接
嗨,在使用Mac的小伙伴么!你是否在Mac操作系统上尝试设置和配置PPPoE连接,却不知道怎么设置?别担心,今天我将为你一步步教你如何在Mac上进行设置和配置。无论你是新手还是有经验的用户,本文都将帮助你轻松完…...

Python类的属性和方法
Python类是一种面向对象编程的基本概念,它可以用来创建对象,对象可以拥有属性和方法。 属性是类的特征,它们用于存储对象的状态。属性可以是任何数据类型,例如整数、字符串、列表等。在类中,属性通常定义为类的变量&am…...

C#Queue<T>队列出现弹出元素被最后一次压入得元素覆盖的问题
问题代码: //以下为现有代码的大概描述,只可意会,不可执行!!!Queue<Move> mQueue new Queue<Move>(); //该接口为下面描述线程A、线程B调用的接口 private void ActionTrigger(Move move)//M…...

python3GUI--模仿一些b站网页端组件By:PyQt5(详细介绍、附下载地址)
文章目录 一.前言二.展示1.banner1.静图2.动图 2.一般视频组件1.静图2.动图 3.排行榜1.静图2.动图 三.设计心得(顺序由简到难)1.排行榜2.一般视频组件3.banner 四.总结五.下载地址 一.前言 播客二连发&…...

聚类分析概述
聚类分析(Cluster Analysis)是一种无监督学习方法,用于将数据点划分为具有相似特征的组或簇。聚类分析的目标是使同一簇内的数据点之间的相似性最大化,而不同簇之间的相似性最小化。聚类分析在许多领域中都有广泛的应用࿰…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
