动态不确定性的动态S过程(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

我们展示了如何为建模为线性分数表示并受各种类型的动态不确定性影响的不确定系统组成稳健的稳定性测试。我们的结果是根据线性矩阵不等式制定的,并基于最近建立的有限视界积分二次约束与终端成本的概念。这种约束的构造是由S过程在频域中使用动态拉格朗日乘法器的非常规应用所激发的。我们的技术贡献揭示了如何通过时域中的耗散率参数以无损方式执行这种构造。这为泛化到时变或混合系统开辟了道路。
原文摘要:
We show how to compose robust stability tests for uncertain systems modeled as linear fractional representations and affected by various types of dynamic uncertainties. Our results are formulated in terms of linear matrix inequalities and rest on the recently established notion of finite-horizon integral quadratic constraints with a terminal cost. The construction of such constraints is motivated by an unconventional application of the S-procedure in the frequency domain with dynamic Lagrange multipliers. Our technical contribution reveals how this construction can be performed by dissipativity arguments in the time-domain and in a lossless fashion. This opens the way for generalizations to time-varying or hybrid systems.
📚2 运行结果
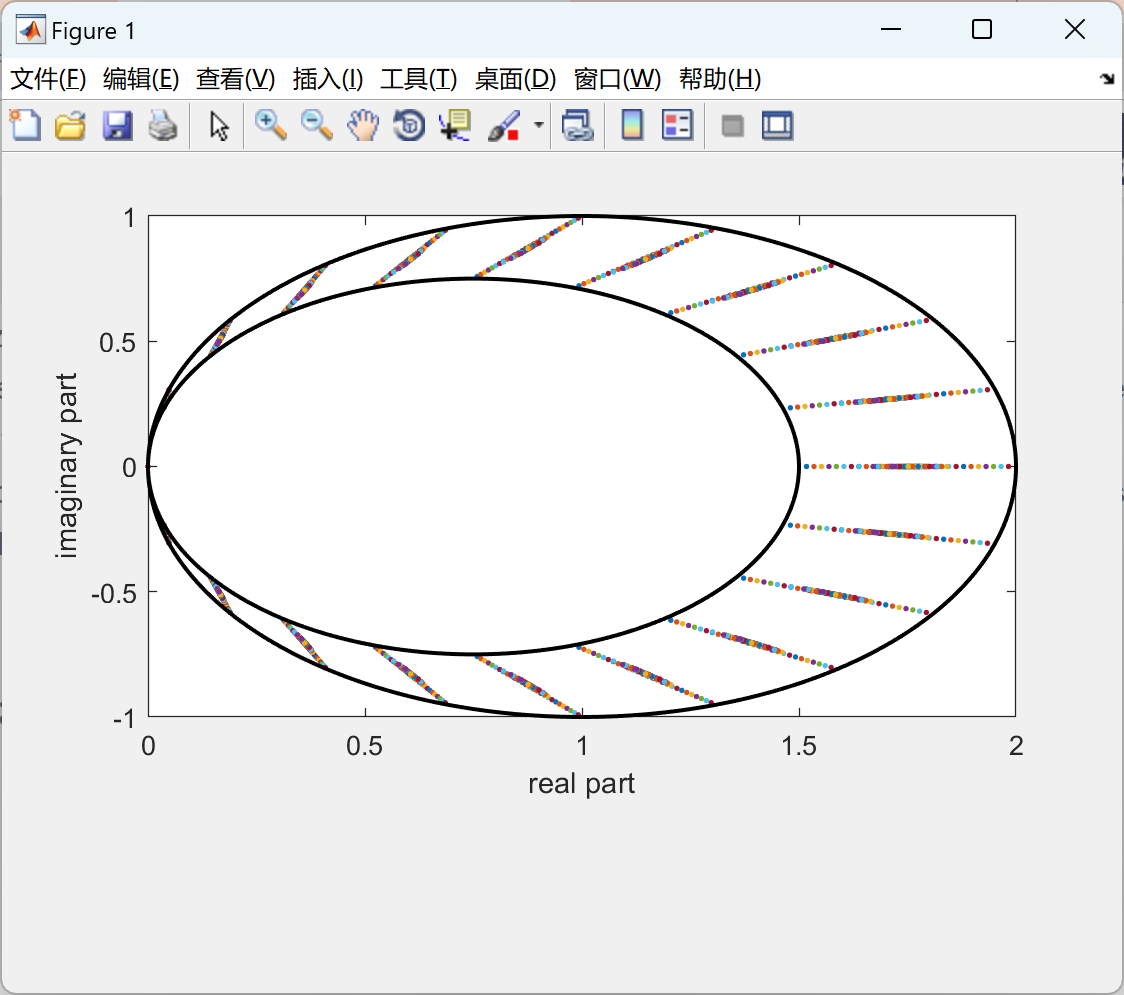
部分代码:
% Involved functions
f1 = @(x) real([1; x(1) + 1i * x(2)]' * [0, 1; 1, -1] * ...
[1; x(1) + 1i * x(2)]); % Outer circle
f2 = @(x) real([1; x(1) + 1i * x(2)]' * [0, -3/4; -3/4, 1] * ...
[1; x(1) + 1i * x(2)]); % Inner circle
% Plotdomain
x = 0:0.01:2;
y = -1:0.01:1;
% Generate grid
[X,Y] = meshgrid(x,y);
% Evaluate functions on grid
Z1 = zeros(length(y), length(x));
Z2 = zeros(length(y), length(x));
for i = 1 : length(y)
for j = 1 : length(x)
Z1(i, j) = f1([x(j); y(i)]);
Z2(i, j) = f2([x(j); y(i)]);
end
end
contour(X,Y,Z1, [0;0], 'linewidth', 1.5, 'color', 'black')
contour(X,Y,Z2, [0;0], 'linewidth', 1.5, 'color', 'black')
xlabel('real part')
ylabel('imaginary part')
%set(gca, 'FontSize', 15)
print('../results/Fig2','-dpng')
%% Gain Bounds
% A very special system, but anyhow
a = -0.1;
% (s + 2 - 1/(del+a)) * (s + del + 1)
sys = ss([(1-3*a)/a, (1-2*a)/a; 1, 0], ...
[-1/a, 0, 1; 0, 0, 0], ...
[a+3+(1-3*a)/a, 1+2*a + (1-2*a)/a; 1, 2; 1, 0], ...
[-1/a, 1, 0; 0, 0, 1; 0, 0, 0]);
% This is constructed in a fashion such that lft(0.5, sys) is unstable
% IO dimensions
p.sys = sys;
p.inp = [2, 1];
p.out = [2, 1];
% Analysis based on covering with single disk. This has to fail since 0.5
% is contained in the disk.
Pi{1} = [0, 1; 1, -1];
ga = ana_rep_intersect(p, Pi);
% More meaningful covering (intersection of interior of a disk and exterior
% of another disk).
Pi{1} = [0, 1; 1, -1];
Pi{2} = [0, -3/4; -3/4, 1];
ga = ana_rep_intersect(p, Pi);
disp(['Gain bound from Theorem 8 with static filter : ', num2str(ga)]);
P = [blkdiag(0, 0), blkdiag(1, -3/4); ...
blkdiag(1, -3/4)', blkdiag(-1, 1)];
ga = ana_rep_region(p, P);
disp(['Gain bound from Theorem 10 with static filter : ', num2str(ga)]);
% Same as above, but with dynamic multipliers
nu = 1;
al = 2;
p.ps = bas(nu, al, p.inp(1));
ga = ana_rep_intersect(p, Pi);
disp(['Gain bound from Theorem 8 with dynamic filter (nu=1): ', ...
num2str(ga)]);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]Tobias Holicki, Carsten W. Scherer (2022) A Dynamic S-Procedure for Dynamic Uncertainties
🌈4 Matlab代码实现
相关文章:

动态不确定性的动态S过程(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
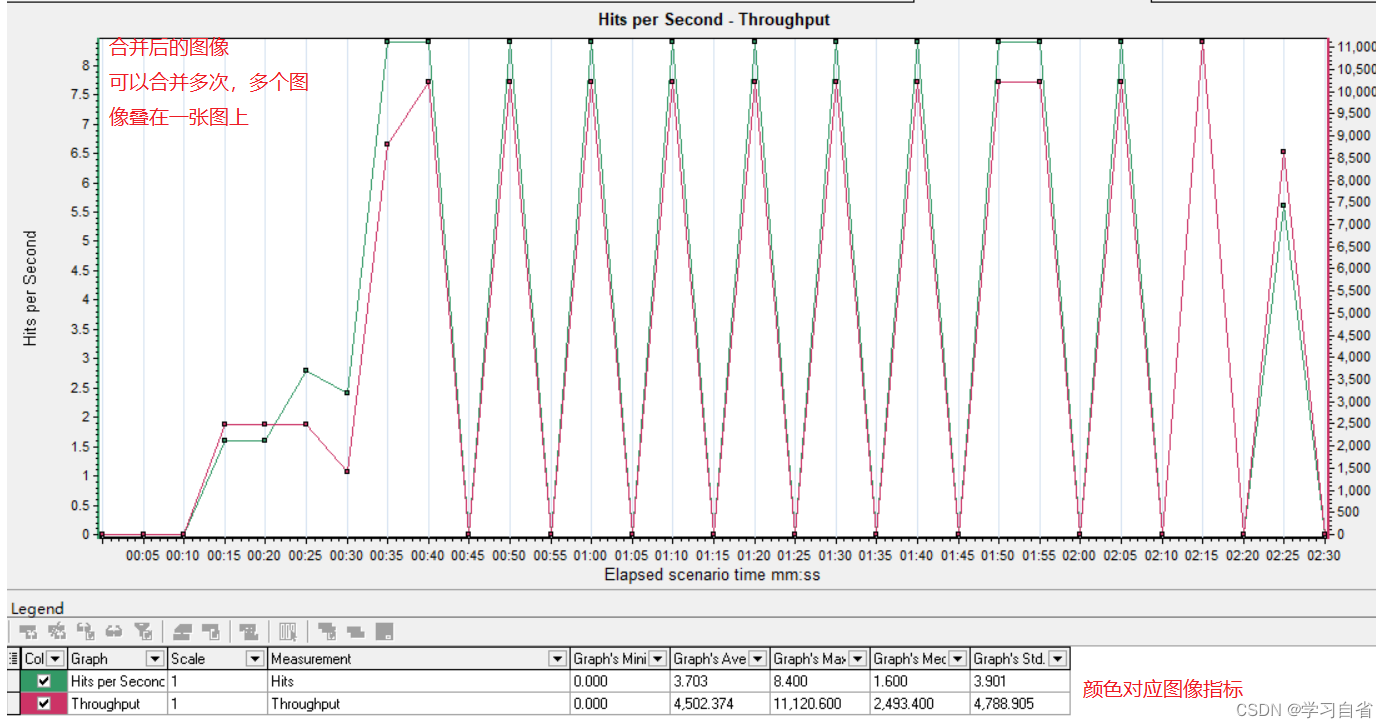
LoadRunner操作教程
日升时奋斗,日落时自省 目录 1、Virtual User Generator (VUG) 1.1、WebTours系统 1.1.1、WebTours启动 1.1.2、WebTours配置 1.2、脚本录制 1.3、编译 1.4、脚本运行 1.5、加强脚本 1.5.1、事务插入 1.5.2、插入集合点 1.5.3、参…...
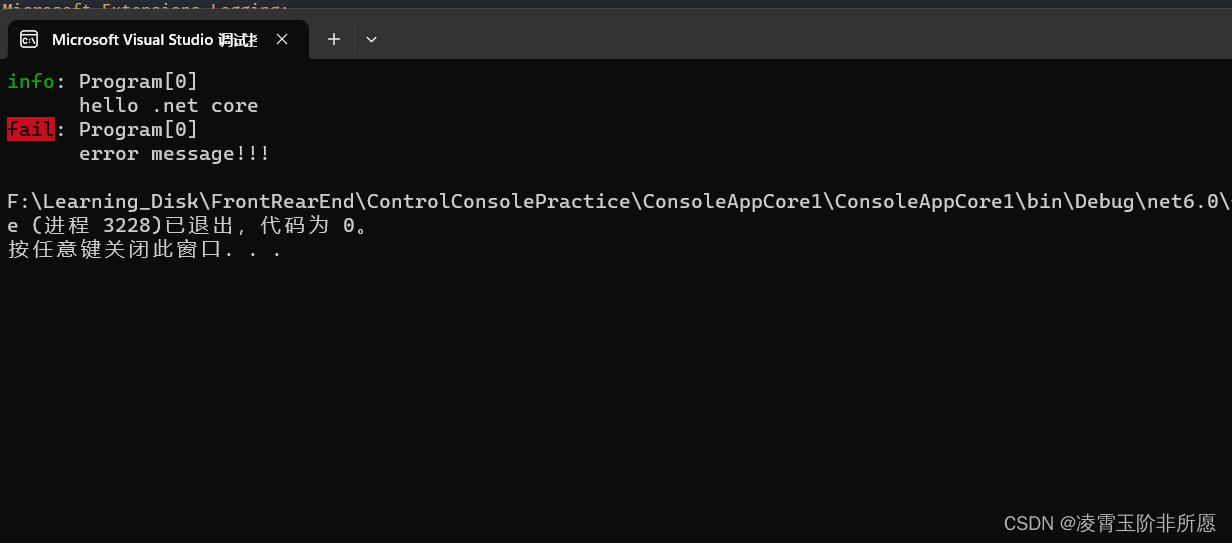
.NET Core 实现日志打印输出在控制台应用程序中
在本文中,我们将探讨如何在 .NET Core 应用程序中将日志消息输出到控制台,从而更好地了解应用程序的运行状况。 .NET Core 实现日志打印输出在控制台应用程序中 在 .NET Core 中,日志输出打印是使用 Microsoft.Extensions.Logging 命名空间…...
Nginx正向代理与反向代理及Minio反向代理实操(三)
本文是对: Nginx安装及Minio集群反向动态代理配置(二) 文的进一步完善: 多台服务器间免密登录|免密拷贝 Cenos7 搭建Minio集群部署服务器(一) Cenos7 搭建Minio集群Nginx统一访问入口|反向动态代理(二) Spring Boot 与Minio整合实现文件上传与下载(三) CentOS7的journa…...

Xmake v2.8.2 发布,官方包仓库数量突破 1k
Xmake 是一个基于 Lua 的轻量级跨平台构建工具。 它非常的轻量,没有任何依赖,因为它内置了 Lua 运行时。 它使用 xmake.lua 维护项目构建,相比 makefile/CMakeLists.txt,配置语法更加简洁直观,对新手非常友好&#x…...

加油站抽烟烟火智能识别算法
加油站抽烟烟火智能识别系统通过yoloopencv网络模型图像识别分析技术,加油站抽烟烟火智能识别算法识别出抽烟和燃放烟火的情况,并发出预警信号以提醒相关人员,减少火灾风险。OpenCV基于C实现,同时提供python, Ruby, Matlab等语言的…...

web前端开发中的响应式布局设计是什么意思?
响应式布局是指网页设计和开发中的一种技术方法,旨在使网页能够在不同大小的屏幕和设备上都能良好地显示和交互。这种方法使得网页可以自动适应不同的屏幕尺寸,包括桌面电脑、平板电脑和手机等。 在Web前端开发中,响应式布局通常使用CSS&…...
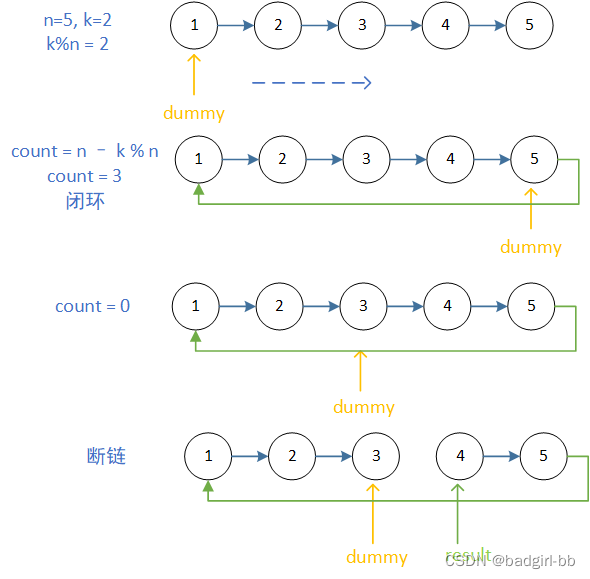
【LeetCode-面试经典150题-day14】
目录 19.删除链表的倒数第N个结点 82.删除排序链表中的重复元素Ⅱ 61. 旋转链表 86.分隔链表 146.LRU缓存 19.删除链表的倒数第N个结点 题意: 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 【输入样例】head [1,2,3,4,5…...

【算法系列总结之分组循环篇】
【算法系列总结之分组循环篇】 分组循环1446.连续字符1869.哪种连续子字符串更长1957.删除字符使字符串变好2038.如果相邻两个颜色均相同则删除当前颜色1759.统计同质子字符串的数目2110.股票平滑下跌阶段的数目1578.使绳子变成彩色的最短时间1839.所有元音按顺序排布的最长子字…...
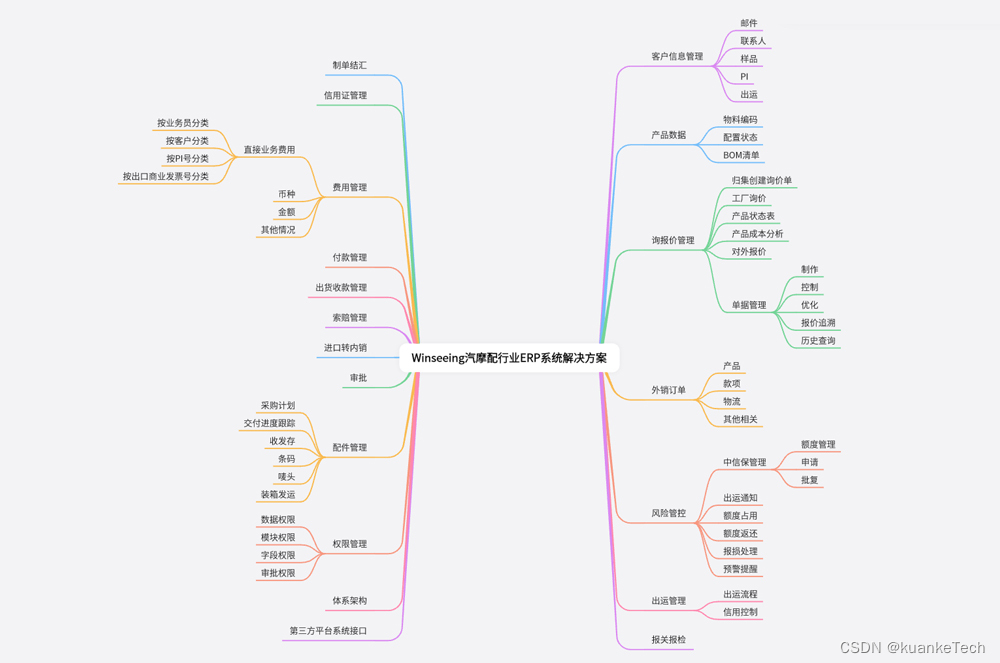
汽车摩托车零部件出口管理ERP解决方案
近年来,随着全球经济的发展,人们对交通工具的需求增加,国内汽车、摩托车市场的不断扩大,以及国内制造技术的不断提高,中国汽车、摩托车零部件出口业务迎来了广阔的发展前景,带动了汽车配件和摩托车配件市场…...

NPM 管理组织包
目录 1、关于组织范围和包 1.1 管理无作用域的包 2、使用组织设置配置npm客户端 2.1 配置您的npm客户端以使用您组织的范围 为所有新包设置组织范围 为单个包设置组织范围 2.2 将默认包可见性更改为public 将单个包的包可见性设置为public 将所有包的包可见性设置为pu…...
)
蓝桥杯上岸每日N题 (修剪灌木)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 不清楚蓝桥杯考什么的点点下方👇 考点秘籍 想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不…...
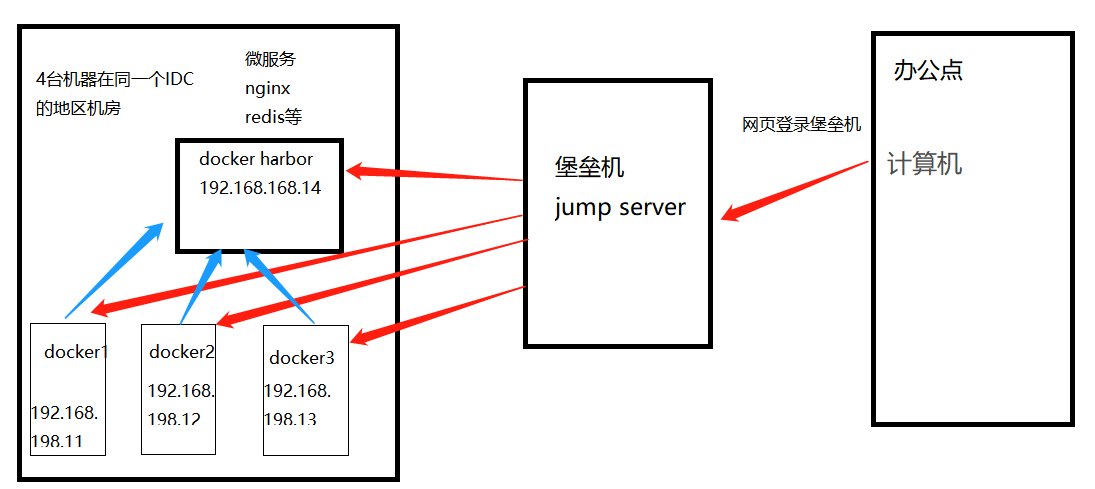
docker harbor私有库
目录 一.Harbor介绍 二.Harbor的特性 三.Harbor的构成 四.Harbor构建Docker私有仓库 4.2在Server主机上部署Harbor服务(192.168.158.25) 4.2.1 这时候这边就可以去查看192.168.158.25网页 4.3此时可真机访问serverIP 4.4通过127.0.0.1来登陆和推送镜…...

strcmp 的使用和模拟
目录 函数介绍: 头文件: 语法: 代码演示: 函数模拟: 函数介绍: strcmp是比较大小的函数。从字符串开始进行比较,如果两个相同位置的字符相同,那么继续往下进行比较,…...

军用加固计算机
军用加固计算机是为满足军事应用需求而设计的一种高性能、高安全性的计算机。与普通计算机相比,它具有以下特点: 加固材料:军用加固计算机通常采用钢板、铝合金等材料进行加固,能够承受较大的冲击和振动,保证在恶劣环境…...

block层:5. 请求分配
请求相关 源码基于5.10 1. 分配请求 static struct request *__blk_mq_alloc_request(struct blk_mq_alloc_data *data) {// 请求队列struct request_queue *q data->q;// 电梯struct elevator_queue *e q->elevator;u64 alloc_time_ns 0;unsigned int tag;// 判断…...
 测试点全过)
L1-038 新世界(Python实现) 测试点全过
题目 这道超级简单的题目没有任何输入。 你只需要在第一行中输出程序员钦定名言“Hello World”,并且在第二行中输出更新版的“Hello New World”就可以了。 输入样例: 无输出样例: Hello World Hello New World题解 """…...
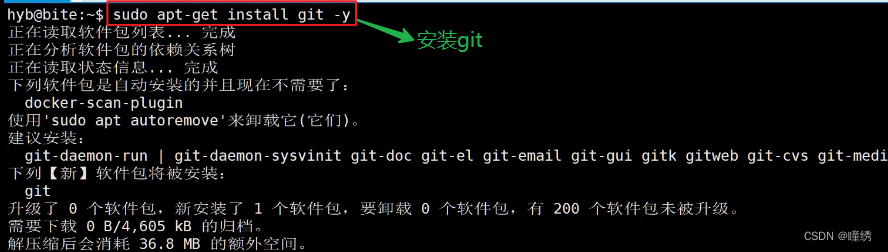
【hello git】初识Git
目录 一、简述Git 二、Linux 下 Git 的安装:CentOS 2.1 基本命令 2.2 示例: 三、Linux 下 Git 的安装:ubuntu 3.1 基本命令 3.2 示例: 一、简述Git Git :版本控制器,记录每次的修改以及版本迭代的一个管…...

Vueelementui动态渲染Radio,Checkbox,笔记
<div id"app"><el-card style"width: 300px"><el-form label-position"top" size"mini"><el-form-item label"标题"><el-input></el-input></el-form-item><el-form-item v-f…...
SpringDataRedis 使用
1. SpringDataRedis 特点2. 使用 SpringDataRedis 步骤3. 自定义 RedisTemplate 序列化4. SpringDataRedis 操作对象 1. SpringDataRedis 特点 提供了对不同 Redis 客户端的整合(Lettuce 和 Jedis)提供了 RedisTemplate 统一 API 来操作 Redis支持 Redi…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...

