(一)连续随机量的生成-基于分布函数
连续随机量的生成-基于分布函数
- 1. 概率积分变换方法(分布函数)
- 2. Python编程实现指数分布的采样
1. 概率积分变换方法(分布函数)
Consider drawing a random quantity X X X from a continuous probability distribution with the distribution function F F F. We know F F F is a continues nondecreasing function if F F F has an inverse F − 1 F^{-1} F−1, then Z = F − 1 ( U ) Z=F^{-1}(U) Z=F−1(U), where U U U is a random quantity drawn from U ( [ 0 , 1 ] ) U([0,1]) U([0,1]), is a random quantity as desired. Indeed,
P ( X ⩽ z ) = P ( F − 1 ( U ) ⩽ z ) = P ( U ⩽ F ( z ) ) = F ( z ) , ∀ z ∈ R P(X \leqslant z)=P\left(F^{-1}(U) \leqslant z\right)=P(U \leqslant F(z))=F(z), \forall z \in \mathbb{R} P(X⩽z)=P(F−1(U)⩽z)=P(U⩽F(z))=F(z),∀z∈R
Example: Exponential distribution Exp ( 1 ) \operatorname{Exp} (1) Exp(1).
Exp (1) has a probability density function: f ( z ) = { e − z , z ⩾ 0 , 0 , z < 0. f(z)= \begin{cases}e^{-z}, & z \geqslant 0, \\ 0, & z<0 .\end{cases} f(z)={e−z,0,z⩾0,z<0.
Its distribution function is F ( z ) = { 1 − e − z , z ⩾ 0 , 0 , z < 0. F(z)= \begin{cases}1-e^{-z}, & z \geqslant 0, \\ 0, & z<0 .\end{cases} F(z)={1−e−z,0,z⩾0,z<0.
We only need to concentrate on F ( z ) F(z) F(z) on [ 0 , ∞ ) [0, \infty) [0,∞), and have
F − 1 ( z ) = − log ( 1 − z ) . F^{-1}(z)=-\log (1-z). F−1(z)=−log(1−z).
So F − 1 ( U ) = − log ( 1 − U ) F^{-1}(U)=-\log (1-U) F−1(U)=−log(1−U) has a probability distribution Exp ( 1 ) (1) (1). Because 1 − U ∼ U ( [ 0 , 1 ] ) 1-U \sim U([0,1]) 1−U∼U([0,1]), we have − log U ∼ Exp ( 1 ) -\log U \sim \operatorname{Exp}(1) −logU∼Exp(1).
For a distribution function which does not have an inverse, we define a generalized inverse as the following:
F − ( z ) = inf { x ∈ R : F ( x ) ⩾ z } . F^{-}(z)=\inf \{x \in \mathbb{R}: F(x) \geqslant z\} . F−(z)=inf{x∈R:F(x)⩾z}.
2. Python编程实现指数分布的采样
Assignment: Sample a random quantity Z ∼ Exp ( λ ) Z \sim \operatorname{Exp}(\lambda) Z∼Exp(λ) for some λ > 0 \lambda>0 λ>0.
import numpy as np
import matplotlib.pyplot as plt# Parameter for the exponential distribution
lambda_value = 0.5# Generate random quantity using CDF method
u = np.random.rand(1000) # Uniform random numbers between 0 and 1
Z = -np.log(1 - u) / lambda_value# Plot histogram
plt.hist(Z, bins=30, density=True, alpha=0.6, color='b', label='Sampled Data')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Histogram of Exponential Distribution (Generated using CDF)')
plt.legend()
plt.grid(True)
plt.show()
相关文章:
连续随机量的生成-基于分布函数)
(一)连续随机量的生成-基于分布函数
连续随机量的生成-基于分布函数 1. 概率积分变换方法(分布函数)2. Python编程实现指数分布的采样 1. 概率积分变换方法(分布函数) Consider drawing a random quantity X X X from a continuous probability distribution with …...

【springboot】Spring Cache缓存:
文章目录 一、导入Maven依赖:二、实现思路:三、代码开发: 一、导入Maven依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-cache</artifactId><…...
)
数学建模-建模算法(4)
python虽然不是完全为数学建模而生的,但是它完整的库让它越来越适合建模了。 - 线性规划:使用scipy.optimize.linprog()函数 python from scipy.optimize import linprogc [-1, 4] A [[-3, 1], [1, 2]] b [6, 4] x0_bounds (None, None) x1_bound…...

python之函数返回数据框
1.原始文件 ##gff-version 3 Chr1A IWGSC_v2.1 gene 40098 70338 33 - . IDTraesCS1A03G0000200;previous_idTraesCS1A02G000100;primconfHC;NameTraesCS1A03G0000200;cdsCDS_OK;mappingfullMatchWithMissmatches Chr1A IWGSC_v2.1 mRN…...

电子商务安全体系架构技术方面
技术方面是本文所要阐述的主要方面,因为它能够依靠企业自 身的努力来达到令人满意的安全保障效果。目前,关于电子商务安全体系的研究比 较多,有基于层次的体系,也有基于对象的体系,还有基于风险管理的体系࿰…...

新安装IDEA 常用插件、设置
新安装IDEA 常用插件、设置 mybatiscodeHelperProRestfulToolkit-fixJrebelmybatis log freepojo to jsonGrep ConsoleMaven HelperCamelCaseCamelCase常用设置 mybatiscodeHelperPro mapper.xml 编码校验 sql 生成,代码生成 RestfulToolkit-fix URI 跳转到对应的…...

ChromeOS 的 Linux 操作系统和 Chrome 浏览器分离
导读科技媒体 Ars Technica 报道称,谷歌正在将 ChromeOS 的浏览器从操作系统中分离出来 —— 让它变得更像 Linux。虽然目前还没有任何官方消息,但这项变化可能会在本月的版本更新中推出。 据介绍,谷歌将该项目命名为 "Lacros"——…...
哔哩哔哩 B站 bilibili 视频倍速设置 视频倍速可自定义
目录 一、复制如下代码 二、在B站视频播放页面进入控制台 三、将复制的代码粘贴到下方输入框,并 回车Enter 即可 四、然后就可以了 一、复制如下代码 (该代码用于设置倍速为3,最后的数值是多少就是多少倍速,可以带小数点&#…...
Lazada商品详情接口 获取Lazada商品详情数据 Lazada商品价格接
一、引言 随着电子商务的迅速发展和普及,电商平台之间的竞争也日趋激烈。为了提供更好的用户体验和更高效的后端管理,Lazada作为东南亚最大的电商平台之一,开发了一种商品详情接口(Product Detail API)。该接口允许第…...
路由攻击(ospf attack)及C/C++代码实现
开放式最短路径优先(OSPF)是应用最广泛的域内路由协议之一。不幸的是,它有许多严重的安全问题。OSPF上的伪造是可能导致路由循环和黑洞的最关键的漏洞之一。 大多数已知的OSPF攻击基于伪造攻击者控制的路由器的链路状态通告(LSA&…...

nginx配置站点强制开启https
当站点域名配置完SSL证书后,如果要强制开启HTTPS,可以在站点配置文件中加上: #HTTP_TO_HTTPS_START if ($server_port !~ 443){rewrite ^(/.*)$ https://$host$1 permanent; } #HTTP_TO_HTTPS_END 附上完整的配置完SSL证书,强制…...
Jacoco XML 解析
1 XML解析器对比 1. DOM解析器: ○ 优点:易于使用,提供完整的文档树,可以方便地修改和遍历XML文档。 ○ 缺点:对大型文档消耗内存较多,加载整个文档可能会变慢。 ○ 适用场景:适合小型XML文档…...
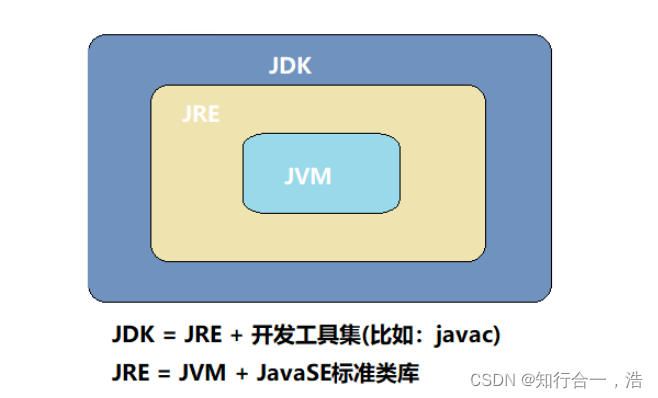
【面试题】JDK(工具包)、JRE(运行环境和基础库)、JVM(java虚拟机)之间的关系?
【面试题】JDK、JRE、JVM之间的关系? JDK(Java Development Kit):Java开发工具包,提供给Java程序员使用,包含了JRE,同时还包含了编译器javac与自带的调试工具Jconsole、jstack等。 JRE(Java Runtime Environment):Java运行时环境&…...

软件设计师学习笔记7-输入输出技术+总线+可靠性+性能指标
目录 1.输入输出技术 1.1数据传输控制方式 1.2中断处理过程 2.总线 3.可靠性 3.1可靠性指标 3.2串联系统与并联系统 3.3混合模型 4.性能指标 1.输入输出技术 即CPU控制主存与外设交互的过程 1.1数据传输控制方式 (1)程序控制(查询)方式&…...

Windows下MATLAB调用Python函数操作说明
MATLAB与Python版本的兼容 具体可参看MATLAB与Python版本的兼容 操作说明 操作说明请参看下面两个链接: 操作指南 简单说明: 我安装的是MATLAB2022a和Python3.8.6(安装时请勾选所有可以勾选的,包括路径)。对应版本安…...
【android12-linux-5.1】【ST芯片】驱动与HAL移植后数据方向异常
ST的传感器驱动与HAL一直成功后,能拿到数据了,但是设备是横屏,系统默认是竖屏。就会出现屏幕自动转动时方向是错的的情况,设备横立展示的是竖屏,设备竖立展示的是横屏。 这个是PCB上设计的传感器贴片方向和横屏不一致…...

JavaScript Es6_3笔记
JavaScript 进阶 文章目录 JavaScript 进阶编程思想面向过程面向对象 构造函数原型对象constructor 属性对象原型原型继承原型链 了解构造函数原型对象的语法特征,掌握 JavaScript 中面向对象编程的实现方式,基于面向对象编程思想实现 DOM 操作的封装。 …...

Qt产生随机数
Qt产生随机数 提问:注意:实现: 提问: 有没有小伙伴遇到这么一种情况,使用rand()和qrand()函数生成的随机数好像不是那么随机,每次都一样。那这种就叫做“伪随机”,因为没有种随机数种子&#x…...

postgresql常用函数-数学函数
postgresql常用函数 简介数学函数算术运算符绝对值取整函数乘方与开方指数与对数整数商和余数弧度与角度常量 π符号函数生成随机数 简介 函数(function)是一些预定义好的代码模块,可以将输入进行计算和处理,最终输出一个 结果值…...

【排序】快速排序(前后指针法)—— 考的最少的一种算法
以从小到大的顺序进行说明。 前后指针法 是指对于一个数组,定义前后各一个指针(prev 和 cur) prev用于卡一个比基准值大的值进行交换cur用于向前遍历出比基准值小的,和prev进行交换 图解 初始化 选出基准值4 如果cur 所在的值…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
