无涯教程-分类算法 - 逻辑回归
逻辑回归是一种监督学习分类算法,用于预测目标变量的概率,目标或因变量的性质是二分法,这意味着将只有两种可能的类。
简而言之,因变量本质上是二进制的,其数据编码为1(代表成功/是)或0(代表失败/否)。
在数学上,逻辑回归模型预测P(Y=1)作为X的函数。它是最简单的ML算法之一,可用于各种分类问题,例如垃圾邮件检测,糖尿病预测,癌症检测等。
逻辑回归类型
通常,逻辑回归是指具有二进制目标变量的二进制逻辑回归,但是可以通过它预测两类以上的目标变量,基于这些类别,Logistic逻辑回归可以分为以下几种类型:
二进制或二项式
在这种类型的分类中,因变量将只有1和0这两种可能的类型,例如,这些变量可以表示成功或失败,是或否,赢或输等。
多项式
在这种分类中,因变量可以具有3种或更多可能的 无序 类型或无定量意义的类型。例如,这些变量可以表示"类型A"或"类型B"或"类型C"。
序数词
在这种分类中,因变量可以具有3种或更多可能的 有序 类型或具有定量意义的类型。例如,这些变量可以表示"差"或"好","非常好","优秀",并且每个类别的分数都可以为0、1、2、3。
逻辑回归假设
在深入研究逻辑回归的实现之前,无涯教程必须了解以下关于相同的假设-
对于二进制逻辑回归,目标变量必须始终为二进制,并且期望输出由因子级别1表示。
模型中不应存在任何多重共线性,这意味着自变量必须彼此独立。
必须在模型中包括有意义的变量。
应该选择较大的样本量进行逻辑回归。
逻辑回归模型
Binary Logistic 模型 - Logistic逻辑回归的最简单形式是二进制或二项式Logistic回归,其中目标或因变量只能具有2种可能的类型,即1或0。
Multinomial Logistic 模型 - Logistic逻辑回归的另一种有用形式是多项式Logistic回归,其中目标或因变量可以具有3种或更多种可能的无序类型,即没有定量意义的类型。
分类算法 - 逻辑回归 - 无涯教程网无涯教程网提供逻辑回归是一种监督学习分类算法,用于预测目标变量的概率,目标或因变量的性质是二分... https://www.learnfk.com/python-machine-learning/machine-learning-with-python-classification-algorithms-logistic-regression.html
https://www.learnfk.com/python-machine-learning/machine-learning-with-python-classification-algorithms-logistic-regression.html
相关文章:

无涯教程-分类算法 - 逻辑回归
逻辑回归是一种监督学习分类算法,用于预测目标变量的概率,目标或因变量的性质是二分法,这意味着将只有两种可能的类。 简而言之,因变量本质上是二进制的,其数据编码为1(代表成功/是)或0(代表失败/否)。 在数学上&…...
URL中传递JSON字符串
今天遇见了一个需求,从post请求中在url里传递json字符串, 就是路径?参数11那种情况 最后怎么解决的呢? 需要使用前端方法,先用JSON.stringify格式化成字符串,再用encodeURIComponent把JSON里面的符号转转为url支持的…...

Python Opencv实践 - Sobel边缘检测
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_GRAYSCALE) print(img.shape)#Sobel边缘检测 #cv.sobel( src, ddepth, dx, dy[,ksize[, scale[, delta[, borderType]]]] ) #src:…...
IDEA快速设置Services窗口
现在微服务下面会有很多SpringBoot服务,Services窗口方便我们管理各个SpringBoot服务,但有时IDEA打开项目后无法的看到Services窗口,以下步骤可以解决!...
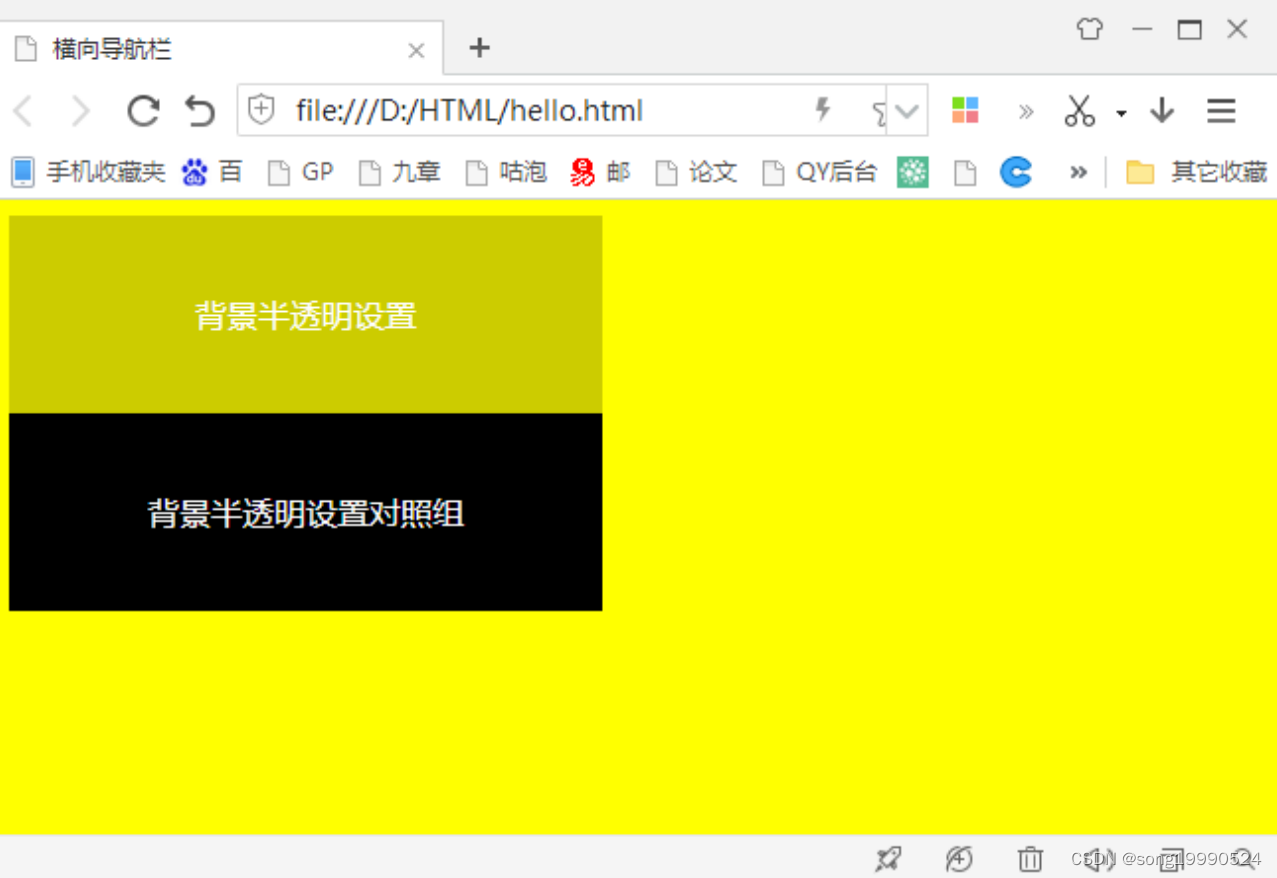
【CSS】CSS 背景设置 ( 背景半透明设置 )
一、背景半透明设置 1、语法说明 背景半透明设置 可以 使用 rgba 颜色值设置半透明背景 ; 下面的 CSS 样式中 , 就是 设置黑色背景 , 透明度为 20% ; background: rgba(0, 0, 0, 0.2);颜色的透明度 alpha 取值范围是 0 ~ 1 之间 , 在使用时 , 可以 省略 0.x 前面的 0 , 直接…...
基于android的学生公寓后勤系统/学生公寓管理系统APP
摘 要 随着网络科技的发展,移动智能终端逐渐走进人们的视线,相关应用越来越广泛,并在人们的日常生活中扮演着越来越重要的角色。因此,关键应用程序的开发成为影响移动智能终端普及的重要因素,设计并开发实用、方便的应…...

跳跃游戏 II
跳跃游戏 II 题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处:0 < j < nums[i] i j < n 返回到达…...

GPT教我学Vue-Router
文章目录 路由的基本配置路由嵌套路由守卫路由参数编程式导航 路由的基本知识点 Vue Router 是 Vue.js 官方的路由管理器。它允许你在 Vue 应用程序中构建单页面应用(SPA),并实现了客户端路由功能。下面是一些 Vue Router 的重要知识点&#…...
Tokenview再度升级:全新Web3开发者APIs数据服务体验!
Tokenview发布全新版本的区块链APIs和数据服务平台,为开发者打造更强大、更便捷的开发体验! 此次升级,我们整合了开发者使用习惯以及Tokenview产品优势。我们深知对于开发者来说,时间是非常宝贵的,因此我们努力提供一…...
?它在JavaScript中有什么作用?请解释一下JavaScript中的“this”关键字的含义和用法。)
什么是原型链(Prototype Chain)?它在JavaScript中有什么作用?请解释一下JavaScript中的“this”关键字的含义和用法。
1、什么是原型链(Prototype Chain)?它在JavaScript中有什么作用? 原型链(Prototype Chain)是一种在JavaScript中创建对象的方式,它允许我们通过继承来扩展对象的属性和方法。 在原型链中,每个对象都有一个…...
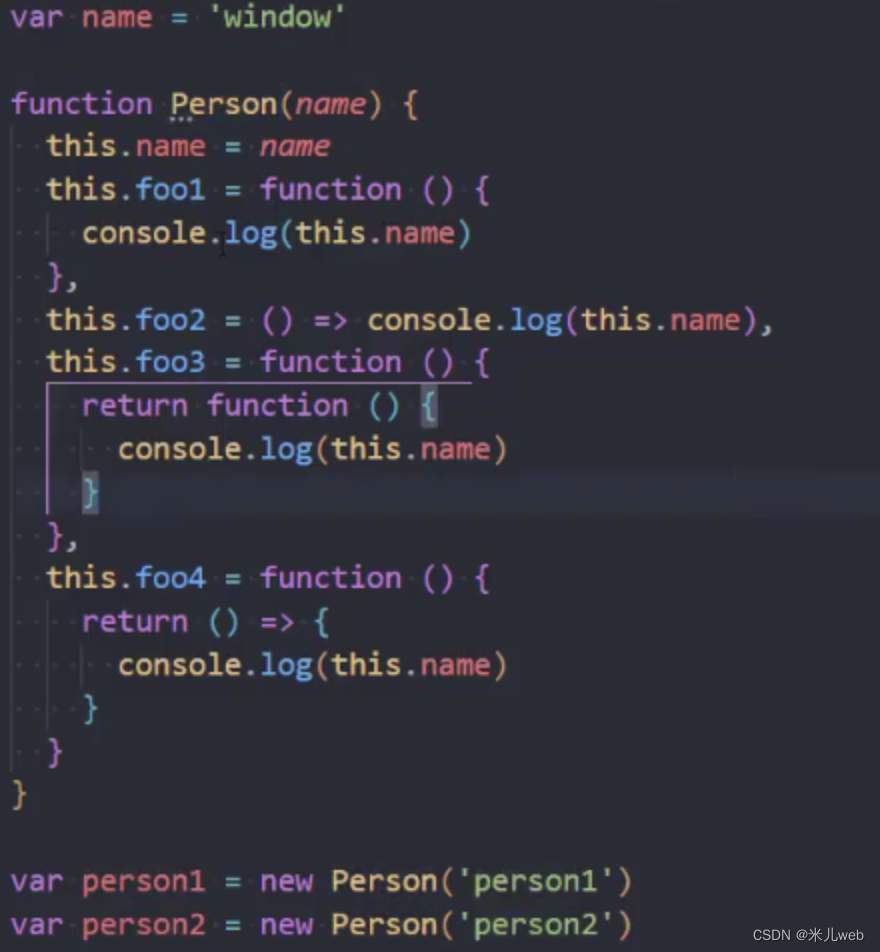
JS-this知识点、面试题
一、this指向什么 1.简介 2.规则一:默认绑定 3.规则二:隐式绑定 4.规则四:new绑定 5.规则三:显式绑定 call、apply、bind 6.内置函数的绑定 7.规则优先级 8.this规则之外--es6剪头函数 9.ES6剪头函数this 二、This面试题 面试题…...

【C++入门到精通】C++入门 —— 多态(抽象类和虚函数的魅力)
阅读导航 前言一、多态的概念1. 概念2. 多态的特点 二、多态的定义及实现1. 多态的构成条件2. 虚函数3. 虚函数的重写⭕虚函数重写的两个例外1.协变(基类与派生类虚函数返回值类型不同)2.析构函数的重写(基类与派生类析构函数的名字不同) 4. override 和 final(C11 …...
基于springboot学生社团管理系统/基于Java的高校社团管理系统的设计与实现
摘 要 随着信息技术和网络技术的飞速发展,人类已进入全新信息化时代,传统管理技术已无法高效,便捷地管理信息。为了迎合时代需求,优化管理效率,各种各样的管理系统应运而生,各行各业相继进入信息管理时代&…...
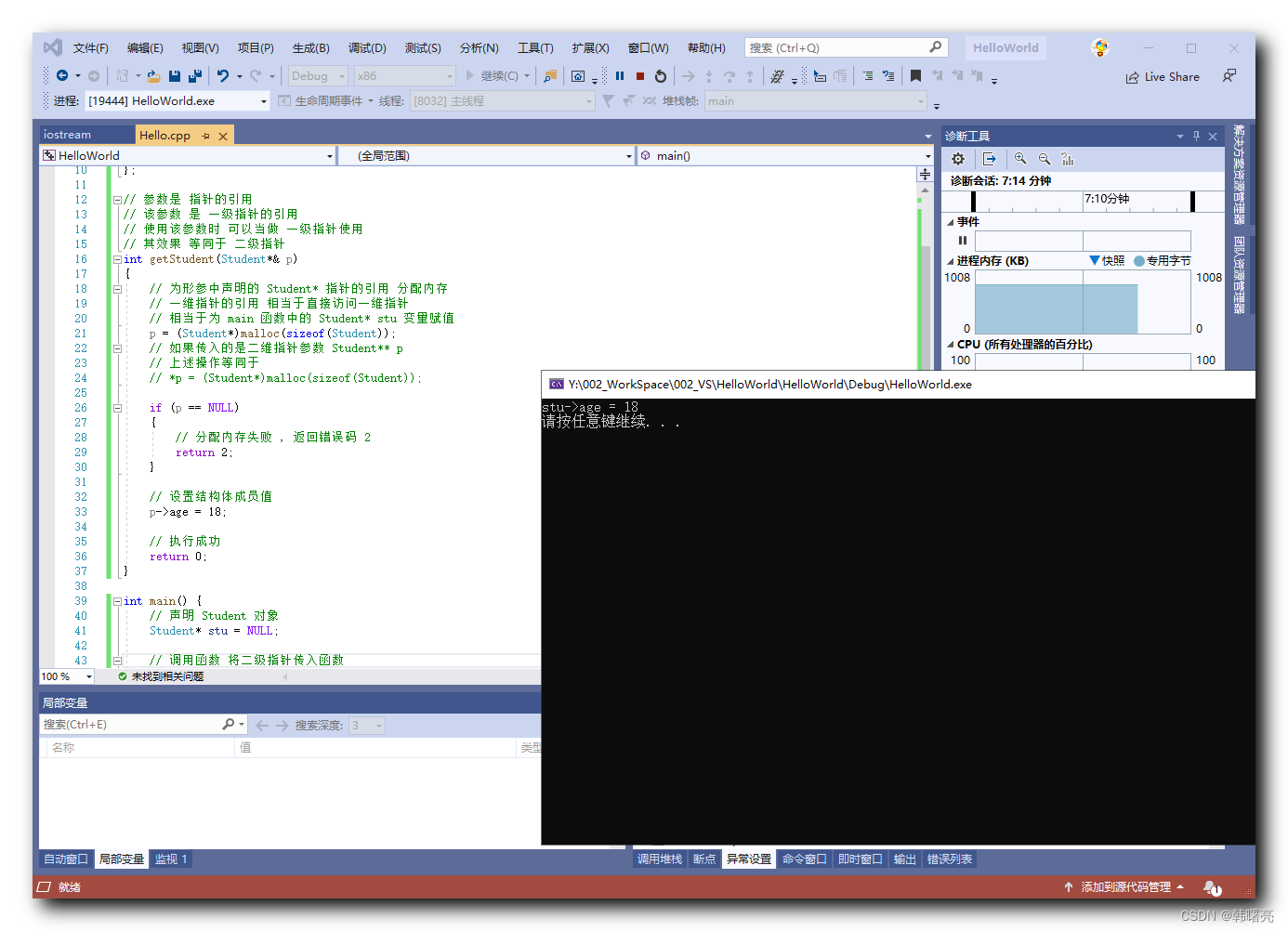
【C++】C++ 引用详解 ⑦ ( 指针的引用 )
文章目录 一、二级指针可实现的效果二、指针的引用1、指针的引用 等同于 二级指针 ( 重点概念 )2、引用本质 - 函数间接赋值简化版本3、代码示例 - 指针的引用 一、二级指针可实现的效果 指针的引用 效果 等同于 二级指针 , 因此这里先介绍 二级指针 ; 使用 二级指针 作为参数 …...

ubuntu安装goland
下载并解压goland sudo tar -C /opt/ -xzvf goland-2023.1.3.tar.gz配置应用图标 新建文件: vim /usr/share/applications/goland.desktop文件中写入如下内容: [Desktop Entry] TypeApplication NameGoLand Icon/opt/GoLand/bin/goland.png Exec/op…...
海康摄像头通过SDK接入到LiveNVR实现双向语音喊话对讲与网页无插件播放,并支持GB28181级联语音对讲...
目录 1、确认摄像头是否支持对讲2、摄像头视频类型复合流3、通道配置SDK接入4、视频广场点击播放5、相关问题 5.1、如何配置通道获取直播流?5.2、如何GB28181级联国标平台?6、RTSP/HLS/FLV/RTMP拉流Onvif流媒体服务 1、确认摄像头是否支持对讲 可以访问摄…...

解锁开发中的创意:用户为中心的设计思维的力量
引言 设计思维,起源于20世纪60年代,是一种解决问题的方法。它不仅仅是设计师的专利,而是一种可以广泛应用于各种行业和领域的方法。设计思维强调了用户至中的重要性,认为任何问题的解决都应该从用户的需求出发。这种方法鼓励我们…...
python+mysql+前后端分离国内职位数据分析(源码+文档+指导)
系统阐述的是使用国内python职位数据分析系统的设计与实现,对于Python、B/S结构、MySql进行了较为深入的学习与应用。主要针对系统的设计,描述,实现和分析与测试方面来表明开发的过程。开发中使用了 Flask框架和MySql数据库技术搭建系统的整体…...

uniapp封装ajax请求
import /common/api/interceptor.js; // 引入拦截器文件 export default{common:{baseUrl:"http://localhost:3000/api",data:{},header:{"Access-Control-Allow-Origin":"*","Content-Type":"application/json","Cont…...

电路原理分析2:应急照明灯电路
k是线圈,1-2(常开)和2-3(常闭)是2个触点。 1、220v交流电正常供电时,变压器触头位置提供12v的电压,这个时候,v2二极管是导通状态,所以线圈k吸合,这个时候1-2…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
