函数的参数传递和返回值-PHP8知识详解
本文学习的是《php8知识详解》中的《函数的参数传递和返回值》。主要包括:向函数传递参数值、向函数传递参数引用、函数的返回值。

1、向函数传递参数值
函数是一段封闭的程序,有时候,程序员需要向函数传递一些数据进行操作。可以接受传入参数的函数定义形式如下:
function 函数名称(参数1,参数2){算法描述,其中使用参数1和参数2;
}向函数传递参数值,示例代码:
<?php
function myFunction($param1, $param2) {// 在函数中使用传递的参数echo "参数1的值为:" . $param1 . "<br>";echo "参数2的值为:" . $param2 . "<br>";
}// 调用函数并传递参数值
myFunction("Hello", "World");?>
在PHP8中的运行结果为:
参数1的值为:Hello
参数2的值为:World
在上述示例中,我们定义了一个名为myFunction的函数,它接受两个参数$param1和$param2。在函数体内,我们使用echo语句打印出传递的参数值。最后,我们通过调用myFunction函数并传递参数值"Hello"和"World"来执行函数。
2、向函数传递参数引用
向函数传递参数引用就是将参数的内存地址传递到函数中。此时,函数内部的所有操作都会影响调用参数值。
使用引用传递方式传值时只需要在原来的基础上加上“&”即可。
向函数传递参数引用,示范代码:
<?php
$a = 10;
$b = 20;
function sum(&$a,$b){$a = $a * $b;echo "求积运算的结果为:$a";
}
sum($a,$b);
echo "<br>";
sum($a,$b);
echo "<br>";
sum($a,$b);
?>
这段代码展示了一个名为sum的函数在PHP中的使用。首先,变量a被赋值10,变量b被赋值20。
然后定义了一个名为sum的函数,并传入两个参数-引用参数a和普通参数b。在函数内部,
a与b相乘的结果赋值给了$a本身,即它是一个引用参数。然后,打印出"a"的结果。
在主程序中,通过调用sum函数,将a和b传递进去并进行求积运算,并输出结果。由于$a是引用参数,在每次调用sum函数时,它会保持更新。
因此,上述代码会执行三次sum函数调用,每次打印出不同的求积结果。
以上代码在PHP8中的运行结果为:
求积运算的结果为:200
求积运算的结果为:4000
求积运算的结果为:80000
3、函数的返回值
在上面的例子中,都是把函数运算完成的值直接打印出来。
但是,很多情况下,程序不需要直接打印结果,而是仅仅给出结果,并且把结果传递给调用这个函数的程序,为其所用。
这里需要用到return关键字设置函数的返回值。
函数的返回值,示例代码:
<?php
function sum($a,$b){ //创建函数return $a*$b; //设置函数的返回值
}
echo "求积运算的结果为:".sum(10,20);
?>以上代码在PHP8的运行结果为:
求积运算的结果为:200
到此为止,向函数传递参数值、向函数传递参数引用、函数的返回值。就讲解完毕了。
space
相关文章:

函数的参数传递和返回值-PHP8知识详解
本文学习的是《php8知识详解》中的《函数的参数传递和返回值》。主要包括:向函数传递参数值、向函数传递参数引用、函数的返回值。 1、向函数传递参数值 函数是一段封闭的程序,有时候,程序员需要向函数传递一些数据进行操作。可以接受传入参…...

【Redis】 Redis短连接的性能优化
Redis短连接的性能优化 1. 问题 通过历史监控我们可以发现用户在频繁使用短连接的时候Redis的cpu使用率有显著的上升 2. 排查 通过扁鹊查看但是Redis的cpu运行情况如下 从扁鹊我们可以看到Redis在freeClient的时候会频繁调用listSearchKey,并且该函数占用了百分…...

无涯教程-分类算法 - 逻辑回归
逻辑回归是一种监督学习分类算法,用于预测目标变量的概率,目标或因变量的性质是二分法,这意味着将只有两种可能的类。 简而言之,因变量本质上是二进制的,其数据编码为1(代表成功/是)或0(代表失败/否)。 在数学上&…...
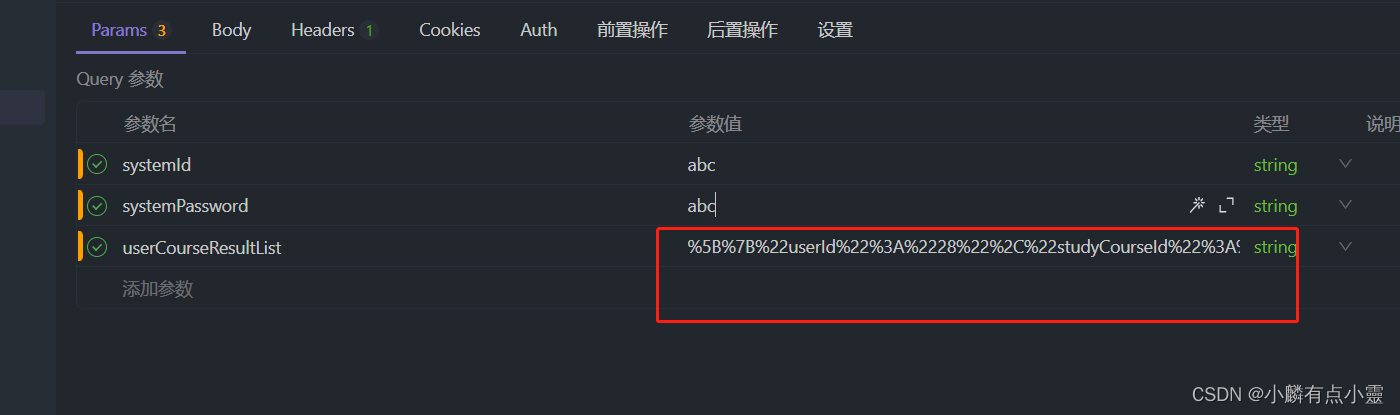
URL中传递JSON字符串
今天遇见了一个需求,从post请求中在url里传递json字符串, 就是路径?参数11那种情况 最后怎么解决的呢? 需要使用前端方法,先用JSON.stringify格式化成字符串,再用encodeURIComponent把JSON里面的符号转转为url支持的…...

Python Opencv实践 - Sobel边缘检测
import cv2 as cv import numpy as np import matplotlib.pyplot as pltimg cv.imread("../SampleImages/pomeranian.png", cv.IMREAD_GRAYSCALE) print(img.shape)#Sobel边缘检测 #cv.sobel( src, ddepth, dx, dy[,ksize[, scale[, delta[, borderType]]]] ) #src:…...
IDEA快速设置Services窗口
现在微服务下面会有很多SpringBoot服务,Services窗口方便我们管理各个SpringBoot服务,但有时IDEA打开项目后无法的看到Services窗口,以下步骤可以解决!...
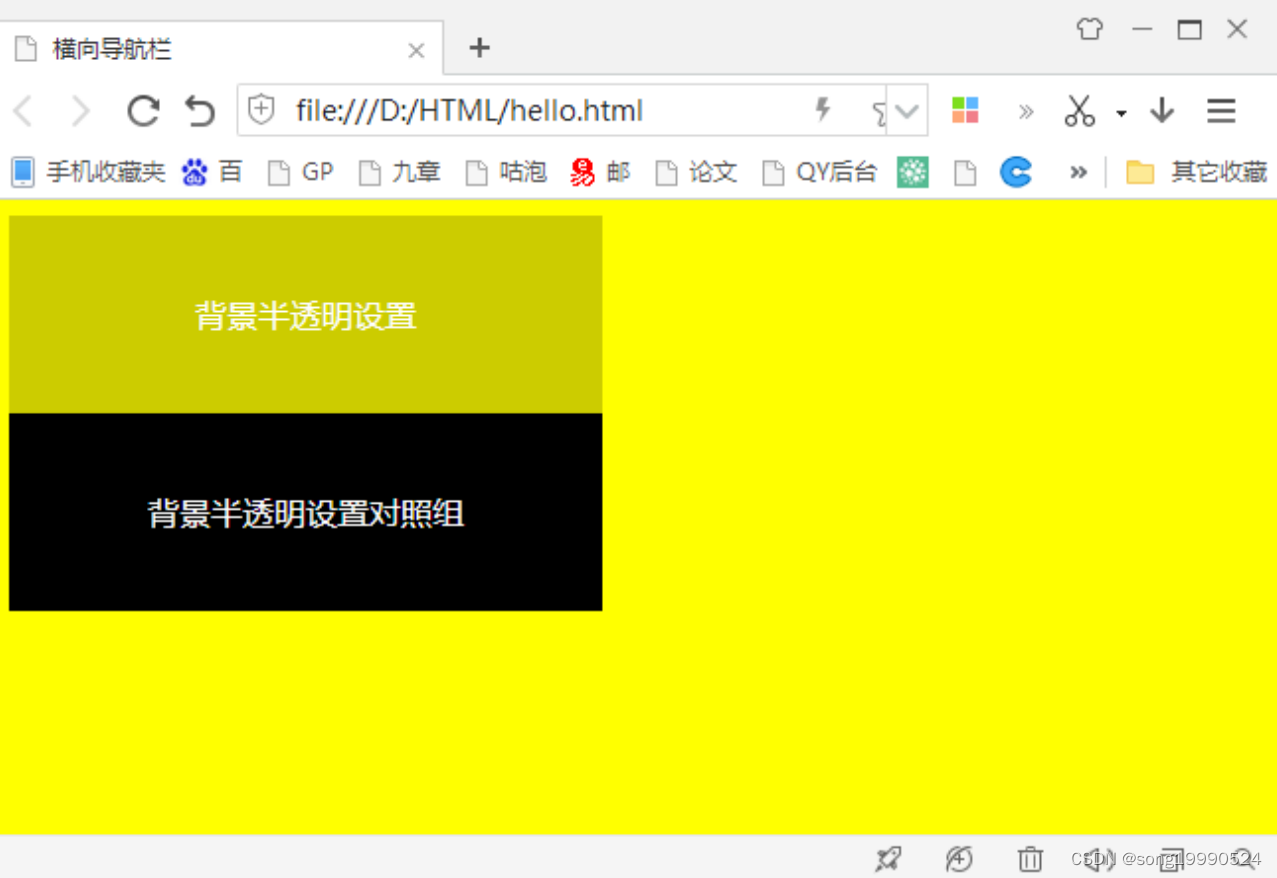
【CSS】CSS 背景设置 ( 背景半透明设置 )
一、背景半透明设置 1、语法说明 背景半透明设置 可以 使用 rgba 颜色值设置半透明背景 ; 下面的 CSS 样式中 , 就是 设置黑色背景 , 透明度为 20% ; background: rgba(0, 0, 0, 0.2);颜色的透明度 alpha 取值范围是 0 ~ 1 之间 , 在使用时 , 可以 省略 0.x 前面的 0 , 直接…...
基于android的学生公寓后勤系统/学生公寓管理系统APP
摘 要 随着网络科技的发展,移动智能终端逐渐走进人们的视线,相关应用越来越广泛,并在人们的日常生活中扮演着越来越重要的角色。因此,关键应用程序的开发成为影响移动智能终端普及的重要因素,设计并开发实用、方便的应…...

跳跃游戏 II
跳跃游戏 II 题目: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处:0 < j < nums[i] i j < n 返回到达…...

GPT教我学Vue-Router
文章目录 路由的基本配置路由嵌套路由守卫路由参数编程式导航 路由的基本知识点 Vue Router 是 Vue.js 官方的路由管理器。它允许你在 Vue 应用程序中构建单页面应用(SPA),并实现了客户端路由功能。下面是一些 Vue Router 的重要知识点&#…...
Tokenview再度升级:全新Web3开发者APIs数据服务体验!
Tokenview发布全新版本的区块链APIs和数据服务平台,为开发者打造更强大、更便捷的开发体验! 此次升级,我们整合了开发者使用习惯以及Tokenview产品优势。我们深知对于开发者来说,时间是非常宝贵的,因此我们努力提供一…...
?它在JavaScript中有什么作用?请解释一下JavaScript中的“this”关键字的含义和用法。)
什么是原型链(Prototype Chain)?它在JavaScript中有什么作用?请解释一下JavaScript中的“this”关键字的含义和用法。
1、什么是原型链(Prototype Chain)?它在JavaScript中有什么作用? 原型链(Prototype Chain)是一种在JavaScript中创建对象的方式,它允许我们通过继承来扩展对象的属性和方法。 在原型链中,每个对象都有一个…...
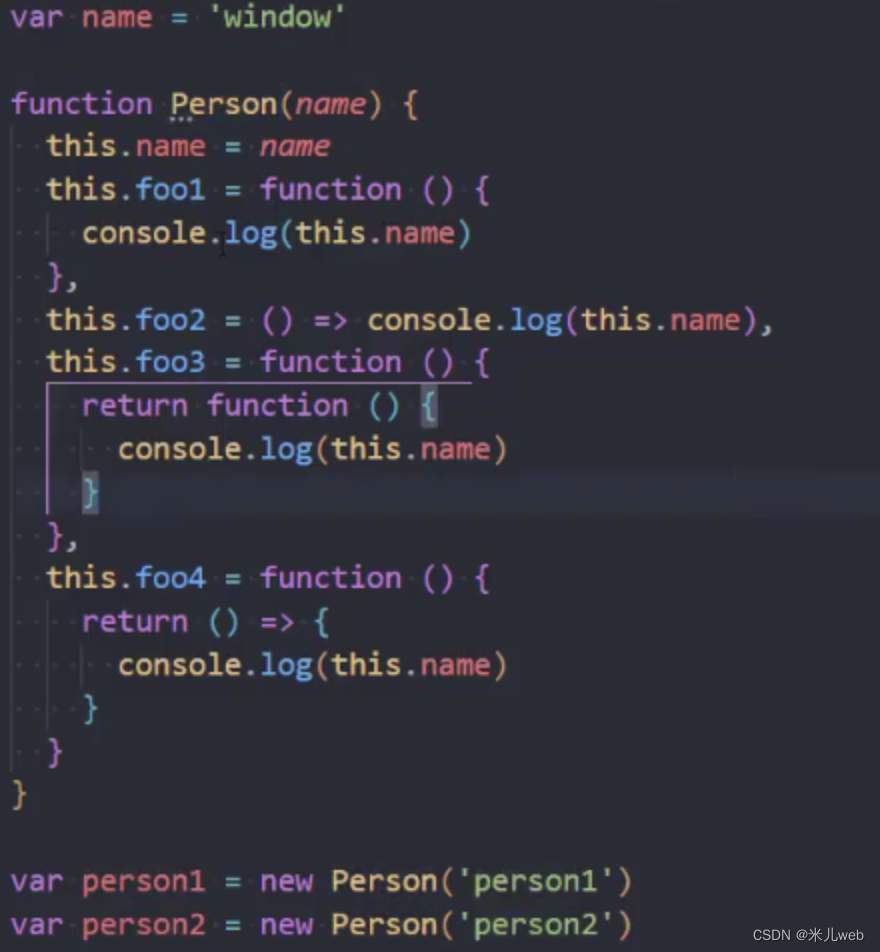
JS-this知识点、面试题
一、this指向什么 1.简介 2.规则一:默认绑定 3.规则二:隐式绑定 4.规则四:new绑定 5.规则三:显式绑定 call、apply、bind 6.内置函数的绑定 7.规则优先级 8.this规则之外--es6剪头函数 9.ES6剪头函数this 二、This面试题 面试题…...

【C++入门到精通】C++入门 —— 多态(抽象类和虚函数的魅力)
阅读导航 前言一、多态的概念1. 概念2. 多态的特点 二、多态的定义及实现1. 多态的构成条件2. 虚函数3. 虚函数的重写⭕虚函数重写的两个例外1.协变(基类与派生类虚函数返回值类型不同)2.析构函数的重写(基类与派生类析构函数的名字不同) 4. override 和 final(C11 …...
基于springboot学生社团管理系统/基于Java的高校社团管理系统的设计与实现
摘 要 随着信息技术和网络技术的飞速发展,人类已进入全新信息化时代,传统管理技术已无法高效,便捷地管理信息。为了迎合时代需求,优化管理效率,各种各样的管理系统应运而生,各行各业相继进入信息管理时代&…...
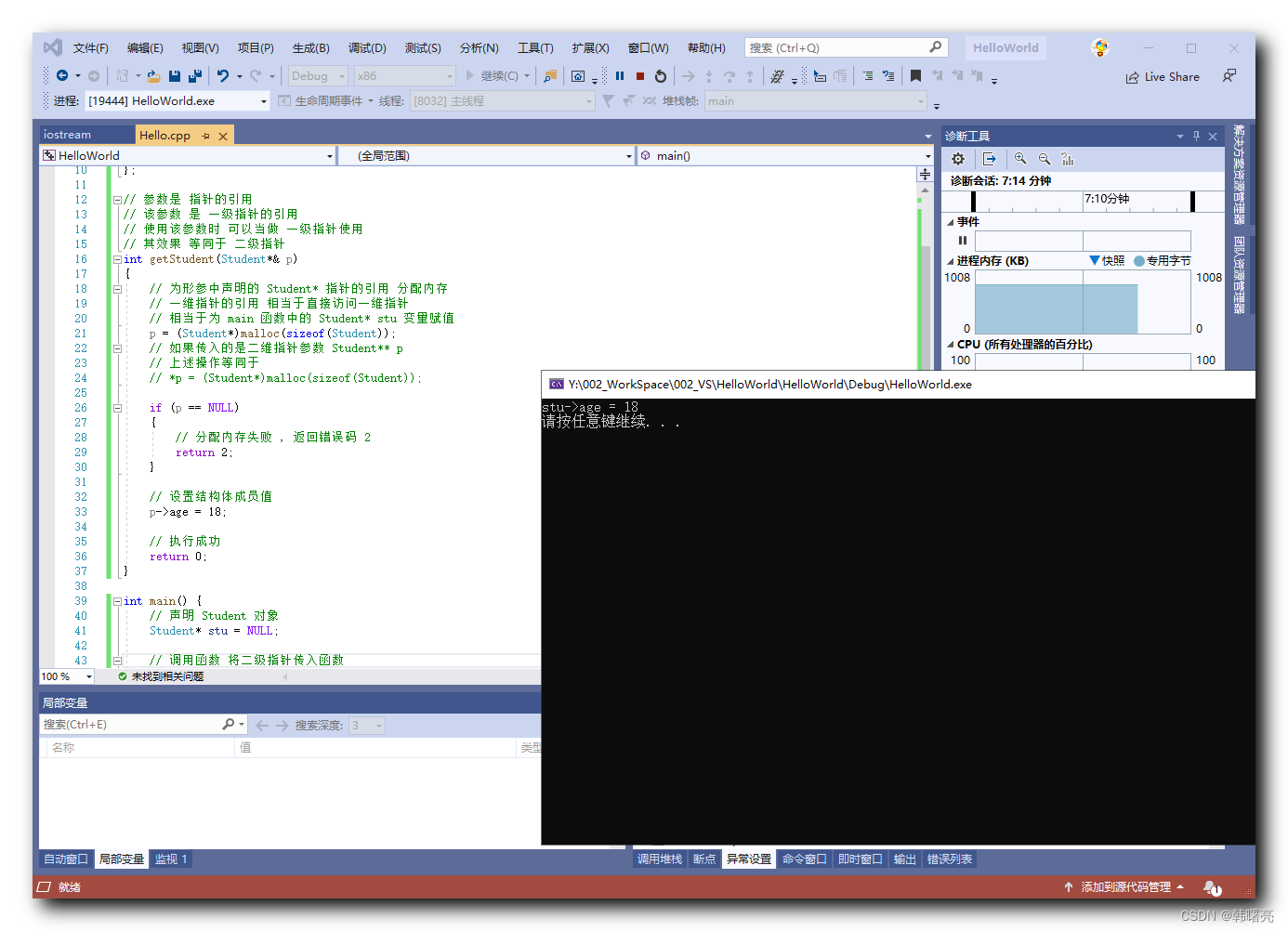
【C++】C++ 引用详解 ⑦ ( 指针的引用 )
文章目录 一、二级指针可实现的效果二、指针的引用1、指针的引用 等同于 二级指针 ( 重点概念 )2、引用本质 - 函数间接赋值简化版本3、代码示例 - 指针的引用 一、二级指针可实现的效果 指针的引用 效果 等同于 二级指针 , 因此这里先介绍 二级指针 ; 使用 二级指针 作为参数 …...

ubuntu安装goland
下载并解压goland sudo tar -C /opt/ -xzvf goland-2023.1.3.tar.gz配置应用图标 新建文件: vim /usr/share/applications/goland.desktop文件中写入如下内容: [Desktop Entry] TypeApplication NameGoLand Icon/opt/GoLand/bin/goland.png Exec/op…...
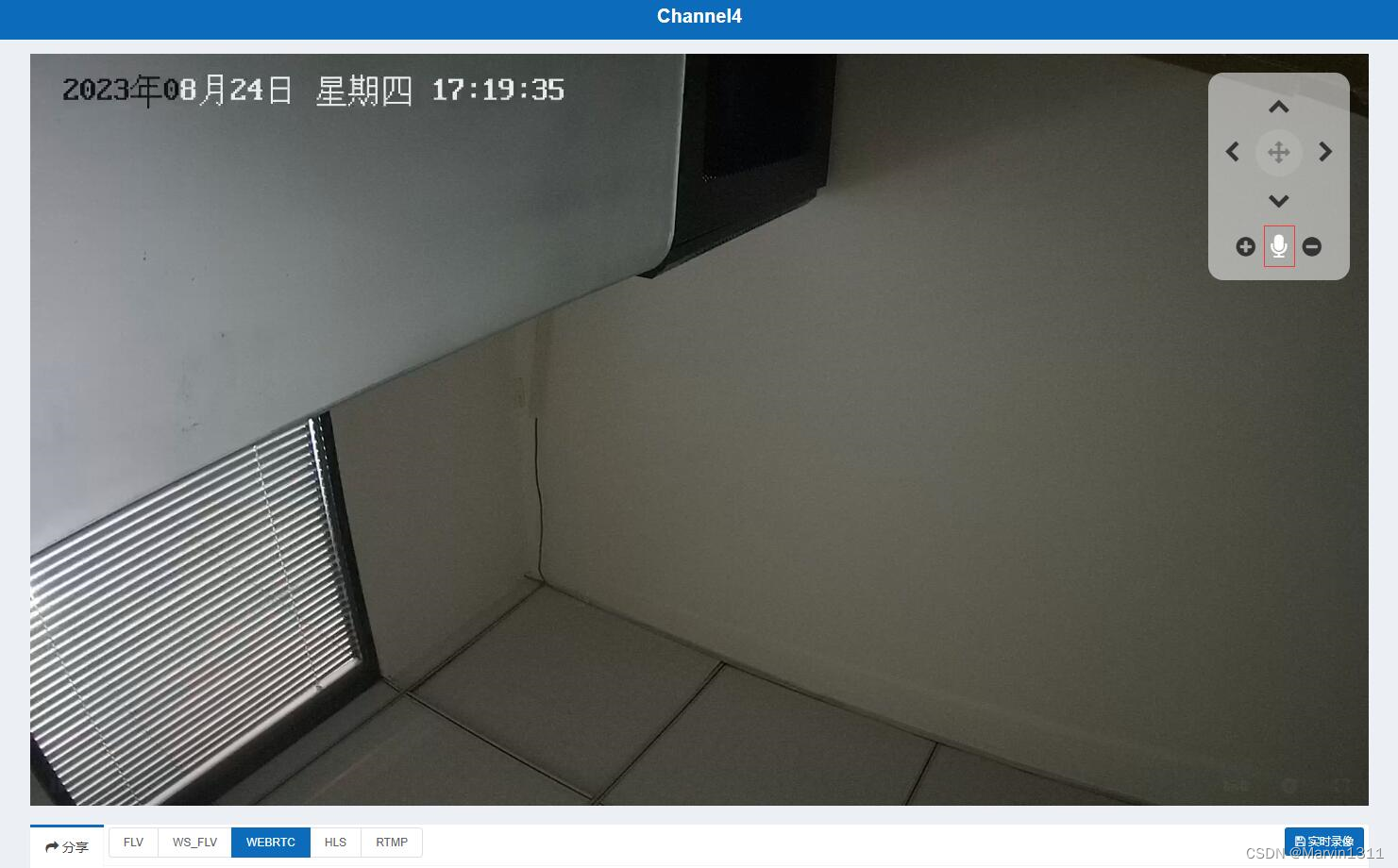
海康摄像头通过SDK接入到LiveNVR实现双向语音喊话对讲与网页无插件播放,并支持GB28181级联语音对讲...
目录 1、确认摄像头是否支持对讲2、摄像头视频类型复合流3、通道配置SDK接入4、视频广场点击播放5、相关问题 5.1、如何配置通道获取直播流?5.2、如何GB28181级联国标平台?6、RTSP/HLS/FLV/RTMP拉流Onvif流媒体服务 1、确认摄像头是否支持对讲 可以访问摄…...

解锁开发中的创意:用户为中心的设计思维的力量
引言 设计思维,起源于20世纪60年代,是一种解决问题的方法。它不仅仅是设计师的专利,而是一种可以广泛应用于各种行业和领域的方法。设计思维强调了用户至中的重要性,认为任何问题的解决都应该从用户的需求出发。这种方法鼓励我们…...
python+mysql+前后端分离国内职位数据分析(源码+文档+指导)
系统阐述的是使用国内python职位数据分析系统的设计与实现,对于Python、B/S结构、MySql进行了较为深入的学习与应用。主要针对系统的设计,描述,实现和分析与测试方面来表明开发的过程。开发中使用了 Flask框架和MySql数据库技术搭建系统的整体…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
