当前位置： 首页 > news >正文

机器学习：异常检测实战

news 2025/8/22 23:00:50

文章目录

  • Anomaly Detection
    • 目录
    • 任务介绍
    • 数据集
    • 方法
    • 评估
    • Baseline
    • 报告
    • 报告评价标准

Anomaly Detection

目录

在这里插入图片描述

任务介绍

在这里插入图片描述
无监督的异常检测

数据集

在这里插入图片描述

方法

在这里插入图片描述
autoencode 是否能够还原出原始类型图片，基于重构loss来判断是否正常
在这里插入图片描述
重构误差当作异常分数

评估

在这里插入图片描述
采用ROC和AUC分数进行评价，不能用acc进行评价。
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Baseline

在这里插入图片描述
三种autoencoder

在这里插入图片描述
后面可以再加一个分类器，训练一个分类器，用分类器的输出是概率分布来表示异常概率。

报告

在这里插入图片描述

报告评价标准

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

相关文章：

机器学习：异常检测实战

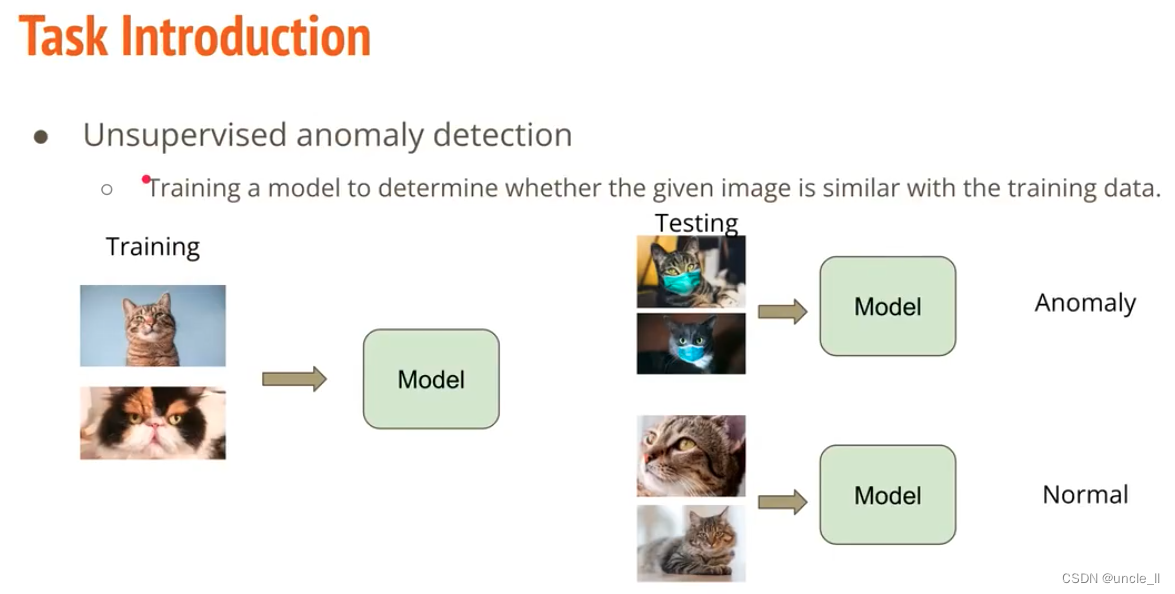
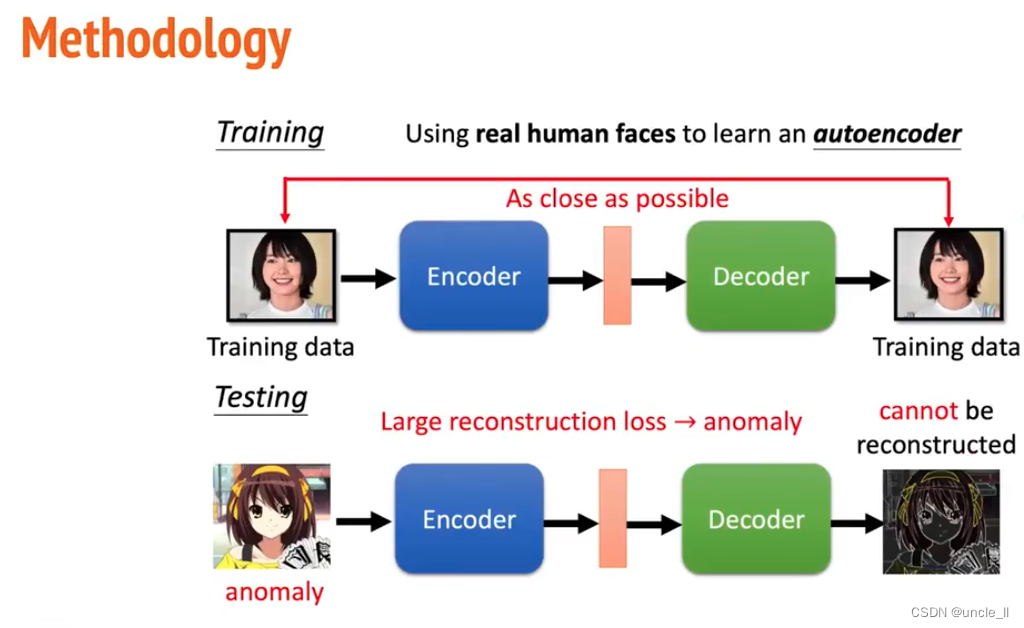
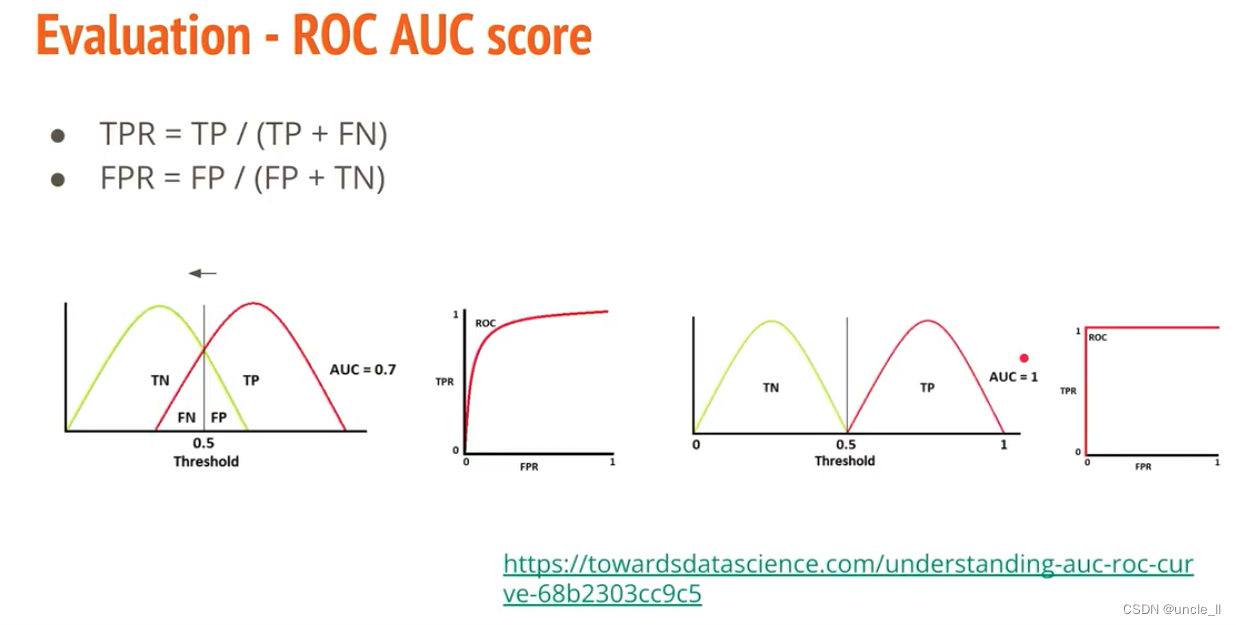
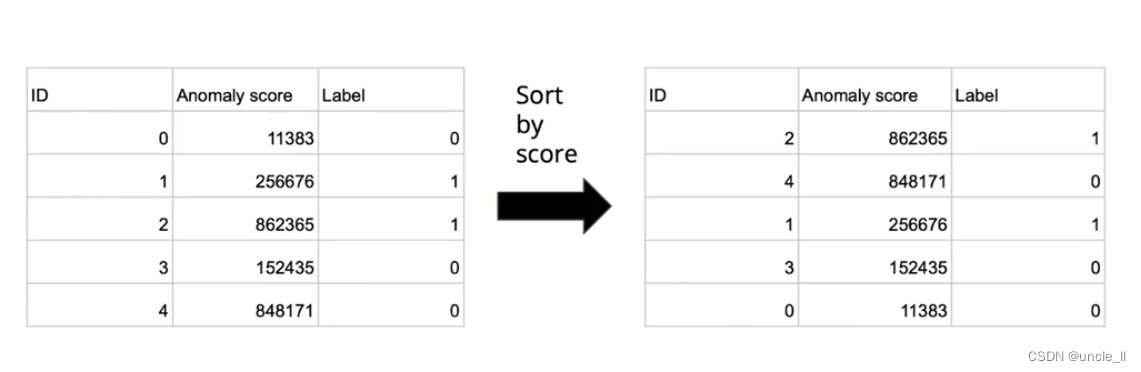
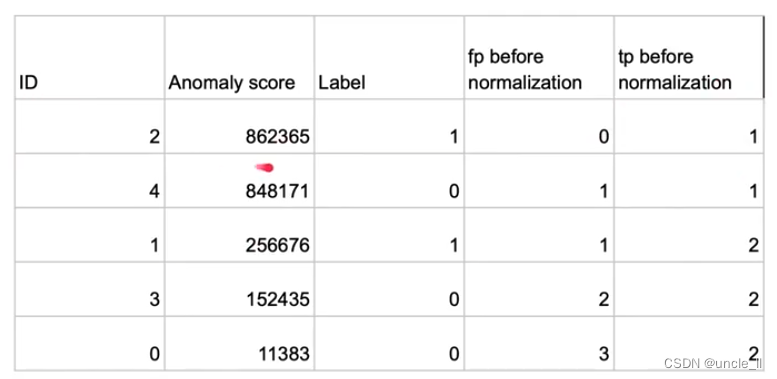
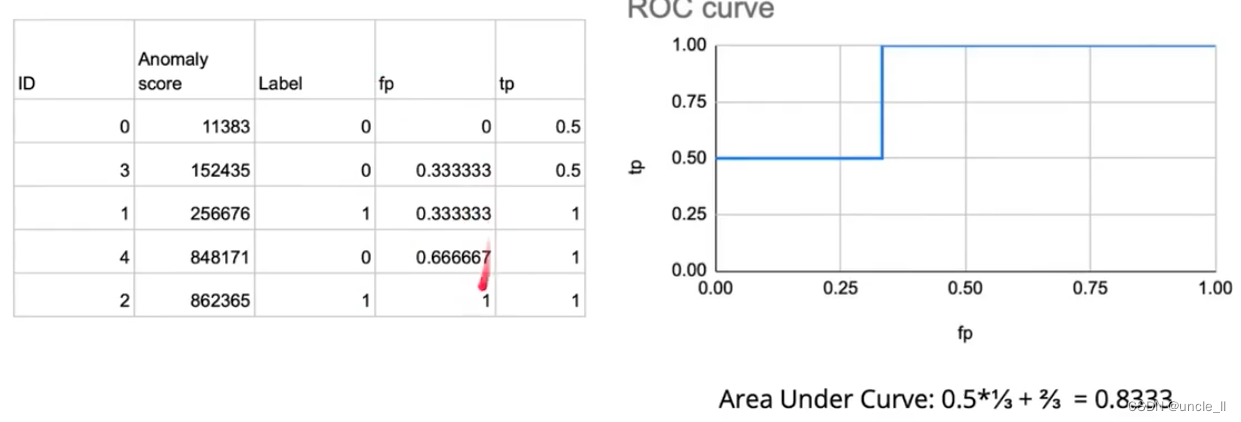
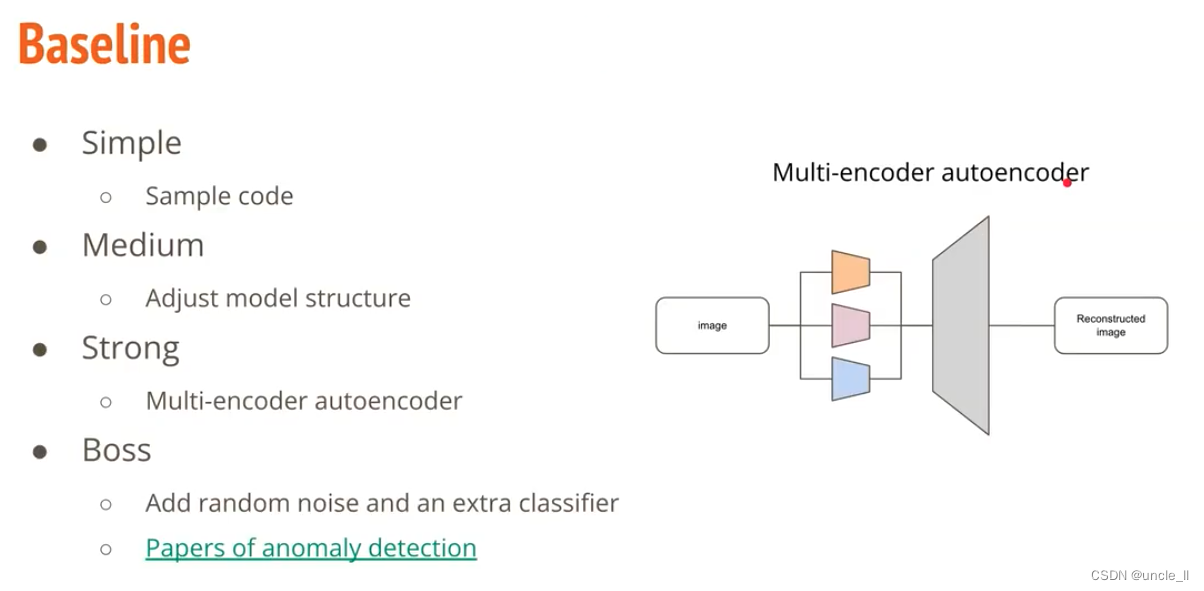
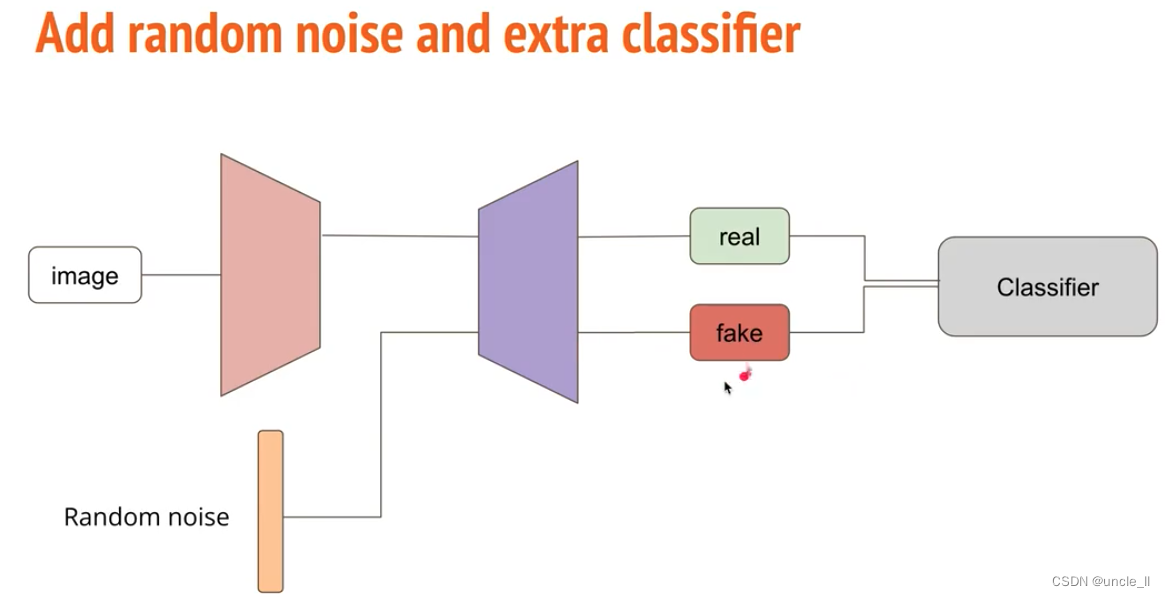
文章目录 Anomaly Detection目录任务介绍数据集方法评估Baseline报告报告评价标准 Anomaly Detection 目录 任务介绍 无监督的异常检测 数据集 方法 autoencode 是否能够还原出原始类型图片，基于重构loss来判断是否正常 重构误差当作异常分数 评估 采用ROC和AUC…...

编程日记 2023/8/28 5:11:26

数据结构1

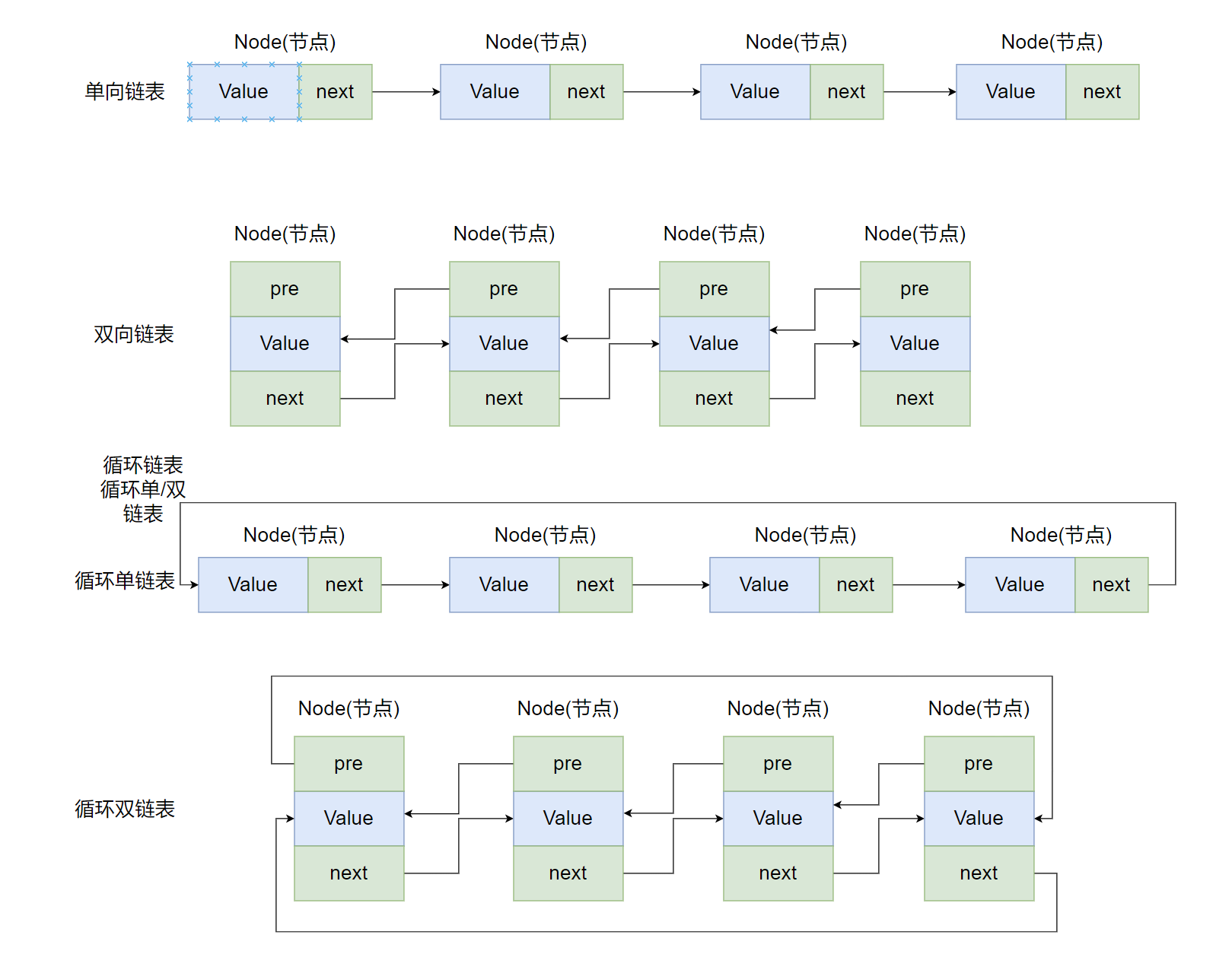
数据结构是计算机科学中存储和组织数据的一种方式，它定义了数据的表示方式和对数据进行操作的方法，常见的数据结构包括数组、栈、链表、队列、树、图等。 目录 一、常见的数据结构 1.数组 2.栈 3.队列 4.链表 5.树 6.图 一、常见的数据结构 1.数…...

编程日记 2023/8/28 5:10:25

自然语言处理学习笔记（七）————字典树效率改进

目录 1. 首字散列其余二分的字典树 2.双数组字典树 3.AC自动机(多模式匹配) （1）goto表 （2）output表 （3）fail表 4.基于双数组字典树的AC自动机 字典树的数据结构在以上的切分算法中已经很快了&#x…...

编程日记 2023/8/28 5:09:23

forEach和map有什么区别，使用场景？

forEach和map有什么区别，使用场景？ 区别什么意思？forEach: 不直接改变原始数组，但可以在回调中更改原始数组。 区别 forEach 和 map 都是数组的常用方法，但它们有不同的目的和用法。下面是它们之间的主要区别以及各自…...

编程日记 2023/8/28 5:08:20

【Spring Boot】SpringBoot完整实现社交网站系统

一个完整的社交网站系统需要涉及到用户登录、发布动态、关注、评论、私信等各方面。这里提供一个简单的实现示例&#xff0c;供参考。 前端代码 前端使用Vue框架&#xff0c;以下是部分代码示例&#xff1a; 登录页&#xff1a; <template><div><input type…...

编程日记 2023/8/28 5:07:18

Modbus转Profinet网关连接三菱变频器博图快速配置

本案例将分享如何使用兴达易控的modbus转profinet网关&#xff08;XD-MDPN100&#xff09;来连接西门子1200系列plc&#xff0c;并实现三菱变频器的485通讯兼容转modbusTCP通信。通过在博图中进行配置&#xff0c;我们可以实现设备之间的连接和通信。 首先&#xff0c;我们需要…...

编程日记 2023/8/28 5:06:17

8.9 【C语言】有关指针的小结

&#xff08;1&#xff09;首先要准确理解指针的含义。 &a是变量a的地址&#xff0c;也可称为变量a的指针。 指针变量是存放地址的变量。 指针变量的值是一个地址。 指针变量也称为地址变量&#xff0c;它的值是地址。 &#xff08;2&#xff09;在C语言中&#xff0c…...

编程日记 2023/8/28 5:05:14

WordPress Nginx伪静态规则设置以及二级目录规则

WordPress Nginx伪静态规则设置以及二级目录规则&#xff08;wordpress不是安装在根目录的情况&#xff09; 根目录下WordPress的伪静态规则&#xff1a; location / {if (-f $request_filename/index.html){rewrite (.*) $1/index.html break;}if (-f $request_filename/ind…...

编程日记 2023/8/28 5:04:12

2023年高教社杯 国赛数学建模思路 - 复盘：人力资源安排的最优化模型

文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 &#xff08;赛题出来以后第一时间在CSDN分享&#xff09; https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

编程日记 2023/8/28 5:03:11

React内置函数之startTransition与useTransition

React内置函数之startTransition&#xff0c;useTransition 在React中&#xff0c;使用startTransition和useTransition这两个内置函数可以帮助我们更好地管理组件的过渡状态。这两个函数的出现&#xff0c;旨在提供一种简单而强大的方式&#xff0c;来处理组件状态的变化&…...

编程日记 2023/8/28 5:02:09

观察者模式简介

概念&#xff1a; 观察者模式&#xff08;Observer Pattern&#xff09;是一种行为型设计模式&#xff0c;用于在对象之间建立一对多的依赖关系&#xff0c;当一个对象的状态发生变化时&#xff0c;其相关依赖对象会自动收到通知并进行相应处理。 特点&#xff1a; 松耦合&a…...

编程日记 2023/8/28 5:01:08

统计程序两个点之间执行的指令数量

环境:支持perf ubuntu安装 apt-get install linux-tools-common linux-tools-generic linux-tools-uname -randroid 一般自带simpleperf 分析 两个点作差, 求中间结果; *(int*)nullptr 0;案例 断点 1 代码 #define SETPOINT(...) do { *(int*)nullptr 0; } while(0…...

编程日记 2023/8/28 5:00:06

时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)

时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价) 目录 时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现基于TSO-XGBoost金枪鱼算…...

编程日记 2023/8/28 4:59:04

java- ConcurrentHashMap 并发

1. ConcurrentHashMap 并发 1.1. 减小锁粒度 减小锁粒度是指缩小锁定对象的范围&#xff0c;从而减小锁冲突的可能性&#xff0c;从而提高系统的并发能力。减小锁粒度是一种削弱多线程锁竞争的有效手段&#xff0c;这种技术典型的应用是 ConcurrentHashMap(高性能的 HashMap)…...

编程日记 2023/8/28 4:58:03

java练习8.100m小球落地

题目: 如一个小球从100米高度自由落下&#xff0c;每次落地后就反跳回原高度的一半。 那么求它在第10次落地时&#xff0c;共经过多少米&#xff1f;第10次反弹多高&#xff1f; public static void main(String[] args) {/*假如一个小球从100米高度自由落下&#xff0c;每次落…...

编程日记 2023/8/28 4:57:01

Android JNI系列详解之生成指定CPU的库文件

一、前提 这次主要了解Android的cpu架构类型&#xff0c;以及在使用CMake工具的时候&#xff0c;如何指定生成哪种类型的库文件。 如上图所示&#xff0c;是我们之前使用CMake工具默认生成的四种cpu架构的动态库文件&#xff1a;arm64-v8a、armeabi-v7a、x86、x86_64&#xff0…...

编程日记 2023/8/28 4:55:59

Leetcode每日一题：1448. 统计二叉树中好节点的数目

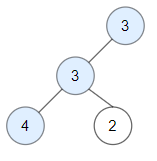
原题 给你一棵根为 root 的二叉树&#xff0c;请你返回二叉树中好节点的数目。 「好节点」X 定义为&#xff1a;从根到该节点 X 所经过的节点中&#xff0c;没有任何节点的值大于 X 的值。 示例 1&#xff1a; 输入&#xff1a;root [3,1,4,3,null,1,5] 输出&#xff1a;4 解…...

编程日记 2023/8/28 4:54:58

华为OD七日集训第2期 - 按算法分类，由易到难，循序渐进，玩转OD（文末送书）

目录 一、适合人群二、本期训练时间三、如何参加四、7日集训第2期五、精心挑选21道高频100分经典题目&#xff0c;作为入门。第1天、逻辑分析第2天、字符串处理第3天、数据结构第4天、递归回溯第5天、二分查找第6天、深度优先搜索dfs算法第7天、动态规划 六、集训总结1、《代码…...

编程日记 2023/8/28 4:53:56

3d max插件CG MAGIC中的蜂窝材质功能可提升效率吗？

工作中能提升效率也都是大家所想的&#xff0c;对于设计师的一个设计过程中&#xff0c;可能想怎么样可以更快呀&#xff0c;是哪个步骤慢了呢&#xff1f; 这样的结果只能说会很多&#xff0c;但是建模这个步骤&#xff0c;肯定是有多无少的。 为了让模型更加逼真&#xff0c…...

编程日记 2023/8/28 4:52:55

一句话木马攻击复现：揭示黑客入侵的实战过程

这篇文章旨在用于网络安全学习&#xff0c;请勿进行任何非法行为&#xff0c;否则后果自负。 准备环境 OWASP虚拟机xfp 7与xshell 7 ​ DVWA系统默认的账号密码均为&#xff1a;admin/admin 1、命令注入中复现 ​ 攻击payload 127.0.0.1 | echo "<?php eval(…...

编程日记 2023/8/28 4:51:53

装饰模式（Decorator Pattern）重构java邮件发奖系统实战

前言 现在我们有个如下的需求&#xff0c;设计一个邮件发奖的小系统&#xff0c; 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式&#xff08;Decorator Pattern&#xff09;允许向一个现有的对象添加新的功能&#xff0c;同时又不改变其…...

编程新知 2025/8/22 21:56:25

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

剑指offer20_链表中环的入口节点

链表中环的入口节点 给定一个链表&#xff0c;若其中包含环&#xff0c;则输出环的入口节点。 若其中不包含环&#xff0c;则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

编程新知 2025/8/22 22:30:54

高危文件识别的常用算法：原理、应用与企业场景

高危文件识别的常用算法&#xff1a;原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件&#xff0c;如包含恶意代码、敏感数据或欺诈内容的文档&#xff0c;在企业协同办公环境中&#xff08;如Teams、Google Workspace&#xff09;尤为重要。结合大模型技术&…...

编程新知 2025/8/18 2:28:17

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2025/8/20 17:01:25

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2025/6/20 15:59:42

RSS 2025｜从说明书学习复杂机器人操作任务：NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill

视觉语言模型&#xff08;Vision-Language Models, VLMs&#xff09;&#xff0c;为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展&#xff0c;机器人仍难以胜任复杂的长时程任务&#xff08;如家具装配&#xff09;&#xff0c;主要受限于人…...

编程新知 2025/8/20 16:04:45

Elastic 获得 AWS 教育 ISV 合作伙伴资质，进一步增强教育解决方案产品组合

作者&#xff1a;来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布&#xff0c;Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明&#xff0c;Elastic 作为 …...

编程新知 2025/8/22 6:11:34

五子棋测试用例

一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏&#xff0c;有着深厚的文化底蕴。通过将五子棋制作成网页游戏&#xff0c;可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家&#xff0c;都可以通过网页五子棋感受到东方棋类…...

编程新知 2025/8/21 14:31:48

​​企业大模型服务合规指南：深度解析备案与登记制度​​

伴随AI技术的爆炸式发展&#xff0c;尤其是大模型&#xff08;LLM&#xff09;在各行各业的深度应用和整合&#xff0c;企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者&#xff0c;还是积极拥抱AI转型的传统企业&#xff0c;在面向公众…...

编程新知 2025/8/21 2:00:40