2022年09月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试

第1题:最长上升子序列
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8). 你的任务,就是对于给定的序列,求出最长上升子序列的长度。
时间限制:11000
内存限制:65536
输入
输入的第一行是序列的长度N (1 <= N <= 1000)。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000。
输出
最长上升子序列的长度。
样例输入
7
1 7 3 5 9 4 8
样例输出
4
要解决最长上升子序列的问题,可以使用动态规划的方法。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdlib.h>int max(int a, int b) {return (a > b) ? a : b;
}int longestIncreasingSubsequence(int arr[], int n) {int dp[1001] = {0};int maxLen = 1;for (int i = 0; i < n; i++) {dp[i] = 1;for (int j = 0; j < i; j++) {if (arr[i] > arr[j]) {dp[i] = max(dp[i], dp[j] + 1);}}maxLen = max(maxLen, dp[i]);}return maxLen;
}int main() {int n;scanf("%d", &n);int arr[1001];for (int i = 0; i < n; i++) {scanf("%d", &arr[i]);}int longestLen = longestIncreasingSubsequence(arr, n);printf("%d\n", longestLen);return 0;
}
该代码使用一个一维数组dp来记录以每个位置上的元素为结尾的最长上升子序列的长度。
首先,将dp数组的初始值全部设为1,因为任意单个元素本身就是一个长度为1的上升子序列。
然后,从第二个位置开始,遍历数组中的每个元素,对于每个元素,再次遍历它之前的元素,如果找到比当前元素小的元素,说明可以将当前元素加入到以该元素结尾的子序列中,更新dp数组的值。
最后,遍历dp数组找到最大的值,即为最长上升子序列的长度。
第2题:神奇的口袋
有一个神奇的口袋,总的容积是40,用这个口袋可以变出一些物品,这些物品的总体积必须是40。John现在有n个想要得到的物品,每个物品的体积分别是a1,a2……an。John可以从这些物品中选择一些,如果选出的物体的总体积是40,那么利用这个神奇的口袋,John就可以得到这些物品。现在的问题是,John有多少种不同的选择物品的方式。
时间限制:10000
内存限制:65536
输入
输入的第一行是正整数n (1 <= n <= 20),表示不同的物品的数目。接下来的n行,每行有一个1到40之间的正整数,分别给出a1,a2……an的值。
输出
输出不同的选择物品的方式的数目。
样例输入
3
20
20
20
样例输出
3
要解决神奇的口袋问题,可以使用递归的方法进行求解。
以下是使用C语言实现的代码:
#include <stdio.h>int count = 0;void magicalPocket(int items[], int n, int idx, int sum) {if (sum == 0) {count++;return;}if (idx == n || sum < 0) {return;}magicalPocket(items, n, idx + 1, sum - items[idx]);magicalPocket(items, n, idx + 1, sum);
}int main() {int n;scanf("%d", &n);int items[21];for (int i = 0; i < n; i++) {scanf("%d", &items[i]);}magicalPocket(items, n, 0, 40);printf("%d\n", count);return 0;
}
该代码使用递归函数magicalPocket来尝试不同的选择物品的方式。
递归函数的参数包括物品数组items、物品数量n、当前处理的物品索引idx和目标总体积sum。
函数首先判断如果目标总体积为0,则表示找到一种选择方式,将count计数器加1并返回。
然后判断如果当前处理的物品索引为n或目标总体积小于0,则返回。
接下来,递归调用函数,分为两种情况:选择当前物品或不选择当前物品。
选择当前物品时,递归调用函数并更新目标总体积为sum - items[idx],同时将物品索引加1。
不选择当前物品时,递归调用函数并保持目标总体积为sum,同时将物品索引加1。
最后,主函数调用magicalPocket函数,并输出count计数器的值,即为不同的选择物品的方式的数目。
第3题:滑雪
Michael喜欢滑雪百这并不奇怪, 因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上,这是最长的一条。
时间限制:1000
内存限制:65536
输入
输入的第一行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行,每行有C个整数,代表高度h,0<=h<=10000。
输出
输出最长区域的长度。
样例输入
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
样例输出
25
要解决滑雪问题,可以使用动态规划的方法。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdbool.h>int max(int a, int b) {return (a > b) ? a : b;
}int longestSlide(int grid[][100], int R, int C, int r, int c, int dp[][100]) {if (dp[r][c] != -1) {return dp[r][c];}int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};int maxLen = 1;for (int i = 0; i < 4; i++) {int newRow = r + directions[i][0];int newCol = c + directions[i][1];if (newRow >= 0 && newRow < R && newCol >= 0 && newCol < C && grid[newRow][newCol] < grid[r][c]) {maxLen = max(maxLen, longestSlide(grid, R, C, newRow, newCol, dp) + 1);}}dp[r][c] = maxLen;return maxLen;
}int main() {int R, C;scanf("%d %d", &R, &C);int grid[100][100];int dp[100][100];for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {scanf("%d", &grid[i][j]);dp[i][j] = -1;}}int maxLength = 0;for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {maxLength = max(maxLength, longestSlide(grid, R, C, i, j, dp));}}printf("%d\n", maxLength);return 0;
}
该代码使用一个二维数组dp来记录从每个位置开始的最长滑坡的长度,以避免重复计算。
首先,将dp数组的初始值全部设为-1,表示尚未计算。
然后,遍历输入的区域二维数组,对于每个位置(r, c),调用longestSlide函数进行递归计算以该位置为起点的最长滑坡长度。
在longestSlide函数中,首先判断如果dp[r][c]已经计算过,则直接返回其值。
然后,定义四个方向的移动数组directions,分别为上、下、左、右。
接下来,遍历四个方向,计算新的行和列的位置,并判断新位置是否在合法范围内且高度小于当前位置的高度。
如果满足条件,则递归调用longestSlide函数并更新maxLen的值。
最后,将dp[r][c]设为maxLen并返回。
最后,主函数遍历整个区域二维数组,找到最大的滑坡长度,并输出。
第4题:删除数字
娇娇一年级了,刚刚学会了识数和比大小。有一天,她在黑板上写上了一串数字:2,1,2,5,4。接着她擦掉了第一个2,发现剩下1,2,4都在自己的位置上,即:1在第1位,2在第2位,4在第4位。
娇娇希望擦掉某些数后,剩下的数列中在自己位置上的数尽量多。她发现这个问题很有趣,想知道最多能有几个数在自己的位置上,请你帮帮她!
时间限制:1000
内存限制:65536
输入
第一行,一个整数 TestNum( ≤ 10),表示测试数据的组数。 接下来每组数据有两行,第一行:一个整数n( ≤ 1000),第二行:n个正整数(≤ 1000)。
输出
对于每组测试数据,输出一个数表示答案。
样例输入
3
5
2 1 2 5 4
7
2 2 3 2 4 5 3
10
1 1 2 2 3 3 4 4 5 5
样例输出
3
4
5
提示
第一组测试数据:擦掉第一个数,1 2 4 有 3 个数在自己的位置上。
第二组测试数据:擦掉第4个、第7个数,2 3 4 5 有 4 个数在自己的位置上。
第三组测试数据:每种相同的数擦掉一个,1 2 3 4 5 有 5 个数在自己的位置上。
要解决删除数字的问题,可以使用贪心算法的思路。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdbool.h>int max(int a, int b) {return (a > b) ? a : b;
}int countNumbers(int numbers[], int n) {int count = 0;for (int i = 0; i < n; i++) {if (numbers[i] == i + 1) {count++;}}return count;
}int maxCountNumbers(int numbers[], int n) {int maxCount = 0;for (int i = 0; i < n; i++) {int temp = numbers[i];numbers[i] = -1;maxCount = max(maxCount, countNumbers(numbers, n));numbers[i] = temp;}return maxCount;
}int main() {int TestNum;scanf("%d", &TestNum);while (TestNum--) {int n;scanf("%d", &n);int numbers[1000];for (int i = 0; i < n; i++) {scanf("%d", &numbers[i]);}int result = maxCountNumbers(numbers, n);printf("%d\n", result);}return 0;
}
该代码使用两个函数来解决问题。
首先,countNumbers函数用于计算给定数字数组中有多少个数字在自己的位置上。
函数遍历数组,对于每个位置i,如果数字numbers[i]的值等于i + 1,则计数器count加1。
最后,返回计数器count的值。
接下来,maxCountNumbers函数用于找到删除数字后最多有多少个数字在自己的位置上。
函数遍历数组,对于每个位置i,将数字numbers[i]暂存到temp变量中,并将该位置的值设为-1,表示删除。
然后,调用countNumbers函数计算删除数字后剩下的数字数组中有多少个数字在自己的位置上,并更新最大值maxCount。
最后,将该位置的值恢复为temp,继续下一次循环。
最后,主函数根据输入的测试组数,循环读取每组测试数据,并调用maxCountNumbers函数计算答案并输出。
相关文章:

2022年09月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:最长上升子序列 一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 < i1 < i2 &…...
二级MySQL(九)——表格数据处理练习
在Mysql中,可以用INSERT或【REPLACE】语句,向数据库中已一个已有的表中插入一行或多行记录。 在Mysql中,可以用【DELETE】或【TRUNCATE】语句删除表中的所有记录。 在Mysql中,可以用【UPDATE】语句来修改数据表中的记录。 为了完…...

QT ListQvector at赋值出错以及解决办法 QT基础入门【QT存储结构】
1、问题 error: passing const QString as this argument discards qualifiers error: assignment of read-only location vec.QVector<int>::at(0) 在Qt中QList,Qvector一般获取元素都是通过at(index)来获取,但是at()的返回是一个const & 常引用,也就是元素不支…...

STM32 CubeMX (H750)RGB屏幕 LTDC
STM32 CubeMX STM32 RGB888 LTDC STM32 CubeMX一、STM32 CubeMX 设置时钟树LTDC使能设置屏幕参数修改RGB888的GPIO 二、代码部分效果 RGB屏幕线束定义: 一、STM32 CubeMX 设置 时钟树 这里设置的时钟,关于刷新速度 举例子:LCD_CLK24MHz 时…...

Redis问题集合(三)在Redis容器里设置键值对
前言 前提是已经拉取了Redis镜像并创建了对应的容器做个记录,方便后续查看 步骤 查看Redis容器的ID:docker ps -a 进入容器:docker exec -it 容器ID /bin/bash进入redis命令行:redis-cli输入密码:auth 配置密码 查看…...
spark中排查Premature EOF: no length prefix available
报错信息 /07/22 10:20:28 WARN DFSClient: Error Recovery for block BP-888461729-172.16.34.148-1397820377004:blk_15089246483_16183344527 in pipeline 172.16.34.64:50010, 172.16.34.223:50010: bad datanode 172.16.34.64:50010 [DataStreamer for file /bdp/data/u9…...

numpy高级函数之where和extract函数
1 numpy.where() 函数返回输入数组中满足给定条件的元素的索引 ---------------------------------------------------- 代码: n1np.random.randint(10,20,10) n2np.where(n1>15) 结果: [17 15 19 15 12 10 16 11 15 13] #原始数组 (array([…...

用Python写一个武侠游戏
前言 在本教程中,我们将使用Python写一个武侠类的游戏,大的框架全部搭好了,很多元素都可以自己添加,让游戏更丰富 📝个人主页→数据挖掘博主ZTLJQ的主页 个人推荐python学习系列: ☄️爬虫JS逆向系列专栏 -…...

Java --- 异常处理
目录 一、什么是异常 二、异常抛出机制 三、如何对待异常 四、 Java异常体系 4.1、Throwable 4.2、Error 4.2、Exception 4.2.1、编译时异常 4.2.2、运行时期异常 五、异常处理 5.1、捕获异常(try-catch) 5.1.2、catch中异常处理方式 …...
CDN/DCDN(全站加速)排查过程中如何获取Eagle ID/UUID
目录 前言1.通过浏览器直接访问文件时获取Request ID 前言 阿里云CDN/DCDN(全站加速)为接收到的每个请求分配唯一的服务器请求ID,作为关联各类日志信息的标识符。当您在使用CDN/DCDN(全站加速)过程中遇到错误且希望阿里云技术支持提供协助时,需要提交失…...

网络安全应急响应预案培训与演练目的
1、增强网络安全意识 网络安全事故隐患往往“生成”于无形。例如,漏洞或黑客攻 击发生之时,受害方企事业单位可能处于非常危险的境地而无所察 觉,一些内部部门人员的网络安全意识也容易懈怠。但不论是内部 员工的疏忽还是管理上的大意&am…...

2023年高教社杯 国赛数学建模思路 - 复盘:校园消费行为分析
文章目录 0 赛题思路1 赛题背景2 分析目标3 数据说明4 数据预处理5 数据分析5.1 食堂就餐行为分析5.2 学生消费行为分析 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 赛题背景 校园一卡通是集…...

7.Oracle视图创建与使用
1、视图的创建与使用 在所有进行的SQL语句之中,查询是最复杂的操作,而且查询还和具体的开发要求有关,那么在开发过程之中,程序员完成的并不是是和数据库的所有内容,而更多的是应该考虑到程序的设计结构。可以没有一个项…...

rust学习-不安全操作
在 Rust 中,不安全代码块用于避开编译器的保护策略 四种不安全操作 解引用裸指针通过 FFI (Foreign Function Interface,外部语言函数接口)调用函数调用不安全的函数内联汇编(inline assembly)解引用裸指针 原始指针(raw pointer,裸指针)* 和引用 &T 有类似的功…...
RHCE——八、DNS域名解析服务器
RHCE 一、概述1、产生原因2、作用3、连接方式4、因特网的域名结构4.1 拓扑4.2 分类4.3 域名服务器类型划分 二、DNS域名解析过程1、分类2、解析图:2.1 图:2.2 过程分析 三、搭建DNS域名解析服务器1、概述2、安装软件3、/bind服务中三个关键文件4、配置文…...

flink cdc初始全量速度很慢原因和优化点
link cdc初始全量速度很慢的原因之一是,它需要先读取所有的数据,然后再写入到目标端,这样可以保证数据的一致性和顺序。但是这样也会导致数据的延迟和资源的浪费。flink cdc初始全量速度很慢的原因之二是,它使用了Debezium作为捕获…...
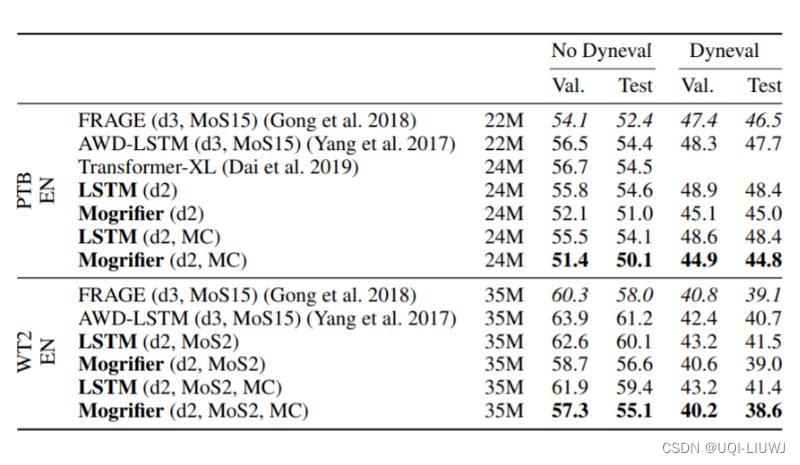
论文笔记: MOGRIFIER LSTM
2020 ICLR 修改传统LSTM 当前输入和隐藏状态充分交互,从而获得更佳的上下文相关表达 1 Mogrifier LSTM LSTM的输入X和隐藏状态H是完全独立的 机器学习笔记:GRU_gruc_UQI-LIUWJ的博客-CSDN博客这篇论文想探索,如果在输入LSTM之前…...

Angular中使用drag and drop实现文件拖拽上传,及flask后端接收
效果:拖拽文件到组件上面时 边框变大变红 松手后发送到服务器(或者点击蓝字手动选择文件)并且把文件名显示在框内,美化还没做 html <div class"drapBox"><div id"drop" (dragenter)"dragenter($event)" (dragov…...

Spring Authorization Server入门 (十六) Spring Cloud Gateway对接认证服务
前言 之前虽然单独讲过Security Client和Resource Server的对接,但是都是基于Spring webmvc的,Gateway这种非阻塞式的网关是基于webflux的,对于集成Security相关内容略有不同,且涉及到代理其它微服务,所以会稍微比较麻…...
配置Flink
配置flink_1.17.0 1.Flink集群搭建1.1解压安装包1.2修改集群配置1.3分发安装目录1.4启动集群、访问Web UI 2.Standalone运行模式3.YARN运行模式4.K8S运行模式 1.Flink集群搭建 1.1解压安装包 链接: 下载Flink安装包 解压文件 [gpbhadoop102 software]$ tar -zxvf flink-1.1…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
生成对抗网络(GAN)损失函数解读
GAN损失函数的形式: 以下是对每个部分的解读: 1. , :这个部分表示生成器(Generator)G的目标是最小化损失函数。 :判别器(Discriminator)D的目标是最大化损失函数。 GAN的训…...

Go 并发编程基础:select 多路复用
select 是 Go 并发编程中非常强大的语法结构,它允许程序同时等待多个通道操作的完成,从而实现多路复用机制,是协程调度、超时控制、通道竞争等场景的核心工具。 一、什么是 select select 类似于 switch 语句,但它用于监听多个通…...
