浙大陈越何钦铭数据结构07-图6 旅游规划
题目:
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
代码及注释:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MAX_VERTEX_NUM 500
#define MAX_DIST 501
#define MAX_COST 501
#define ERROR -1typedef int Vertex;struct _Edge
{Vertex V, W;int dist, cost;
};
typedef struct _Edge *Edge;struct _MGraph
{int Nv, Ne;int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM];int cost[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
};
typedef struct _MGraph *MGraph; /* 以邻接矩阵存储的图的类型 */void InsertEdge(MGraph G, Edge E); // 插入边
MGraph CreateGraph(int vertexNum); // 初始化图
MGraph BuildGraph();Vertex FindMinDist(MGraph G, int dist[], bool collected[]);
void Dijkstra(MGraph G, int dist[], int cost[], Vertex S);Vertex src, dst;
// 对于全局的int数组自动初始化为0,bool数组初始化为false
int dist[MAX_VERTEX_NUM];
int cost[MAX_VERTEX_NUM];
bool collected[MAX_VERTEX_NUM];/*
07-图6 旅游规划
https://pintia.cn/problem-sets/1667128414987735040/exam/problems/1667128415088398337难度:2颗星4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 203 40*/int main()
{MGraph G = BuildGraph();Dijkstra(G, dist, cost, src);printf("%d %d\n", dist[dst], cost[dst]);free(G);return 0;
}MGraph CreateGraph(int vertexNum)
{MGraph G = (MGraph)malloc(sizeof(struct _MGraph));G->Nv = vertexNum;G->Ne = 0;Vertex V, W;for (V = 0; V < vertexNum; V++){for (W = 0; W < vertexNum; W++){G->dist[V][W] = MAX_DIST;G->cost[V][W] = MAX_COST;}}return G;
}void InsertEdge(MGraph G, Edge E)
{/* 插入边<V,W> */G->dist[E->V][E->W] = E->dist;G->cost[E->V][E->W] = E->cost;/* 若是无向图则要反向也插入 */G->dist[E->W][E->V] = E->dist;G->cost[E->W][E->V] = E->cost;
}MGraph BuildGraph()
{MGraph G;Edge E;int Nv, Ne;scanf("%d %d %d %d", &Nv, &Ne, &src, &dst);G = CreateGraph(Nv);if (Ne){G->Ne = Ne;E = (Edge)malloc(sizeof(struct _Edge));for (int i = 0; i < G->Ne; i++){scanf("%d %d %d %d", &E->V, &E->W, &E->dist, &E->cost);InsertEdge(G, E);}free(E);}return G;
}Vertex FindMinDist(MGraph G, int dist[], bool collected[])
{ /* 返回未被收录顶点中dist最小者 */Vertex minV = ERROR;int minDist = MAX_DIST;for (Vertex V = 0; V < G->Nv; V++){if (collected[V] == false && minDist > dist[V]){/* 若V未被收录,且dist[V]更小 */minDist = dist[V]; /* 更新最小距离 */minV = V; /* 更新对应顶点 */}}if (minDist < MAX_DIST) /* 若找到最小dist */return minV; /* 返回对应的顶点下标 */elsereturn ERROR; /* 若这样的顶点不存在,返回错误标记 */
}void Dijkstra(MGraph G, int dist[], int cost[], Vertex S)
{Vertex V, W;/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */for (V = 0; V < G->Nv; V++){dist[V] = G->dist[S][V];cost[V] = G->cost[S][V];}/* 先将起点收入集合 */dist[S] = 0;cost[S] = 0;collected[S] = true;while (1){/* V = 未被收录顶点中dist最小者 */V = FindMinDist(G, dist, collected);if (V == ERROR) /* 若这样的V不存在 */break; /* 算法结束 */collected[V] = true; /* 收录V */for (W = 0; W < G->Nv; W++) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未被收录 */if (collected[W] == false && G->dist[V][W] < MAX_DIST){if (G->dist[V][W] < 0) /* 若有负边 */return; /* 不能正确解决,返回错误标记 *//* 若收录V使得dist[W]变小 */if (dist[V] + G->dist[V][W] < dist[W]){dist[W] = dist[V] + G->dist[V][W]; /* 更新dist[W] */cost[W] = cost[V] + G->cost[V][W];}else if (dist[V] + G->dist[V][W] == dist[W] &&cost[V] + G->cost[V][W] < cost[W]){cost[W] = cost[V] + G->cost[V][W];}}} /* while结束*/
}
ChatGPT对代码的分析,评估:
定义了合适的常量:MAX_DIST 和 MAX_COST 的定义符合题目要求,对于表示距离和花费的最大值都设置为 501,有效地区分了有限距离和无穷远的情况。
创建图和插入边:CreateGraph 和 InsertEdge 函数用于创建图和插入边的操作,实现了初始化图的邻接矩阵并向图中添加边的功能。
构建图:BuildGraph 函数根据输入构建了图,并通过调用 CreateGraph 和 InsertEdge 来创建和填充图的邻接矩阵。
Dijkstra 算法:Dijkstra 函数使用 Dijkstra 算法,根据图的邻接矩阵计算从起点到每个顶点的最短距离和最小花费。在这个过程中,使用了辅助函数 FindMinDist 来选择未被收录顶点中距离最小的顶点。
主函数运行:主函数中先调用 BuildGraph 构建图,然后调用 Dijkstra 计算最短距离和最小花费,并输出结果。
执行结果:
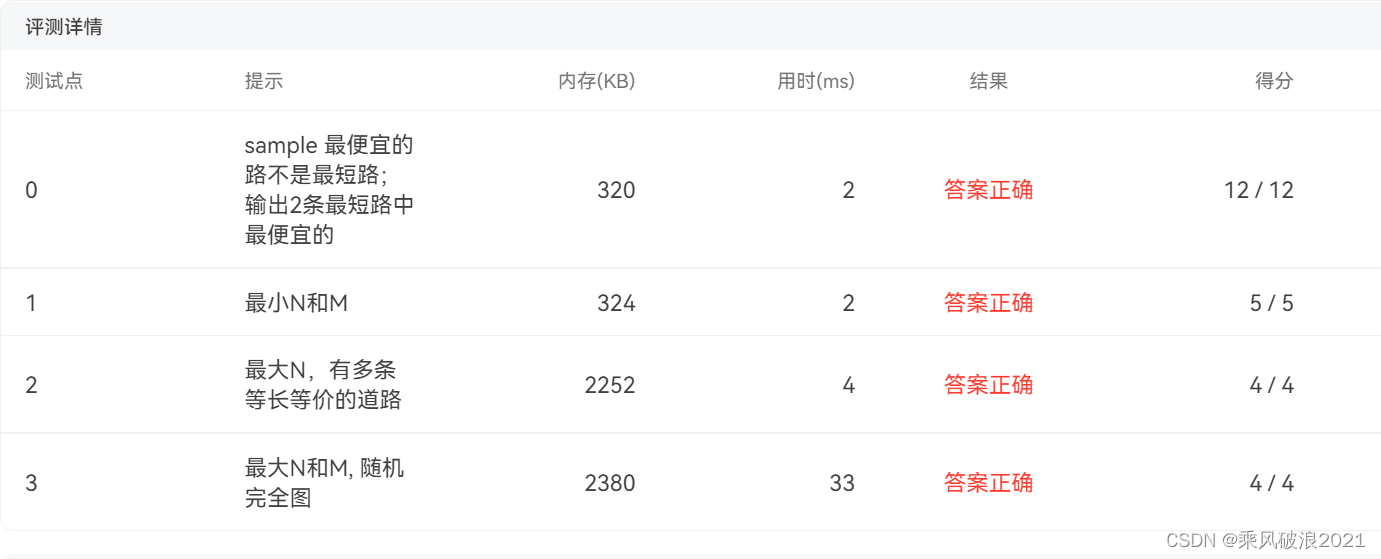
相关文章:

浙大陈越何钦铭数据结构07-图6 旅游规划
题目: 有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。 输入…...
项目登录)
VUE笔记(七)项目登录
1、安装elementui 在终端执行 vue add element 注册组件 如果要使用哪个组件,大家需要在plugins/element.js中注册该组件 import Vue from vue import { Button } from element-ui Vue.use(Button) 在页面组件中使用 <el-button type"primary"&…...
大语言模型之六- LLM之企业私有化部署
数据安全是每个公司不得不慎重对待的,为了提高生产力,降本增效又不得不接受新技术带来的工具,私有化部署对于公司还是非常有吸引力的。大语言模型这一工具结合公司的数据可以大大提高公司生产率。 私有化LLM需要处理的问题 企业内私有化LLM…...
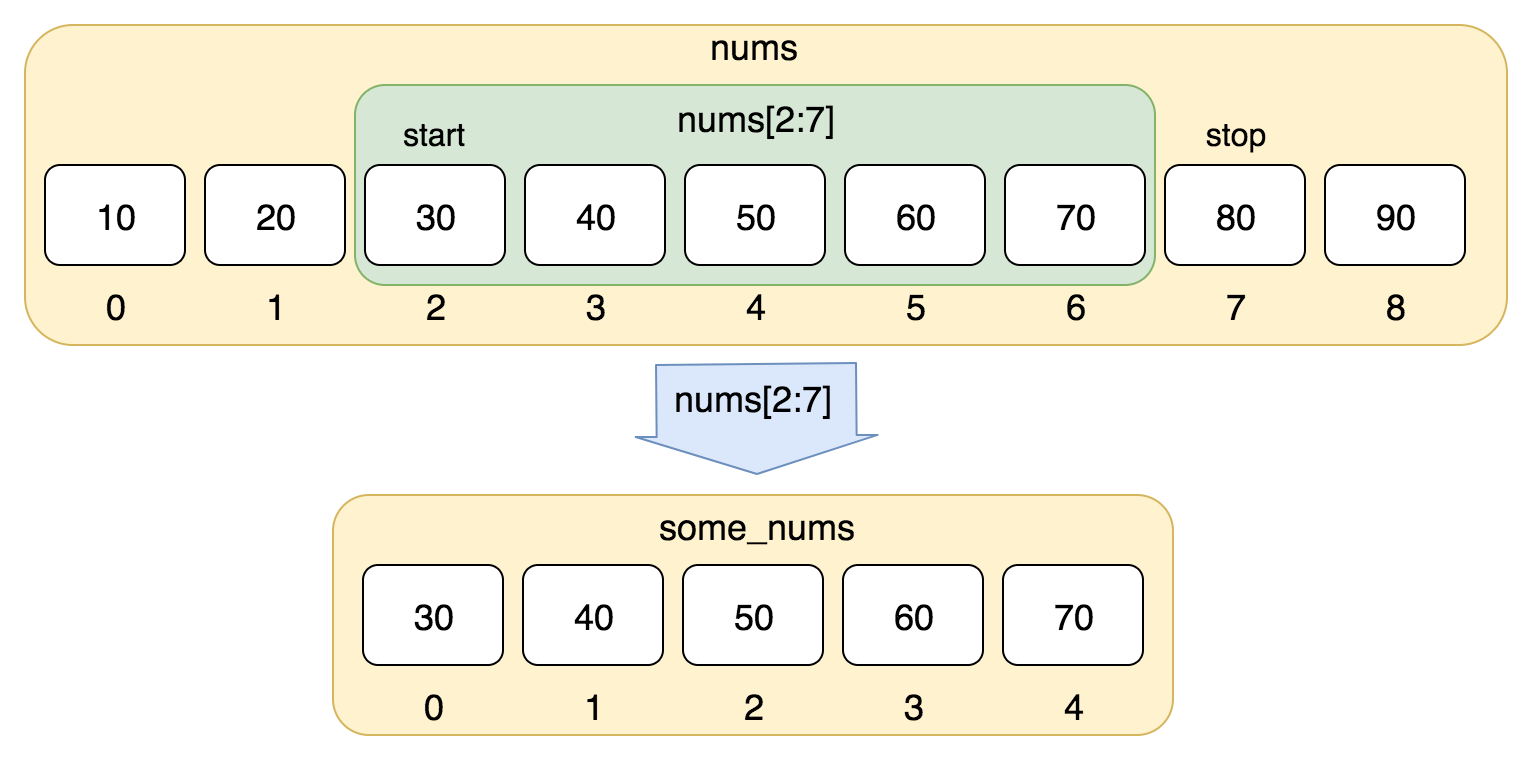
Python3 列表
Python3 列表 序列是 Python 中最基本的数据结构。 序列中的每个值都有对应的位置值,称之为索引,第一个索引是 0,第二个索引是 1,依此类推。 Python 有 6 个序列的内置类型,但最常见的是列表和元组。 列表都可以进…...

OpenCV基础知识(8)— 图形检测
前言:Hello大家好,我是小哥谈。图形检测是计算机视觉的一项重要功能。通过图形检测可以分析图像中可能存在的形状,然后对这些形状进行描绘,例如搜索并绘制图像的边缘,定位图像的位置,判断图像中有没有直线、…...
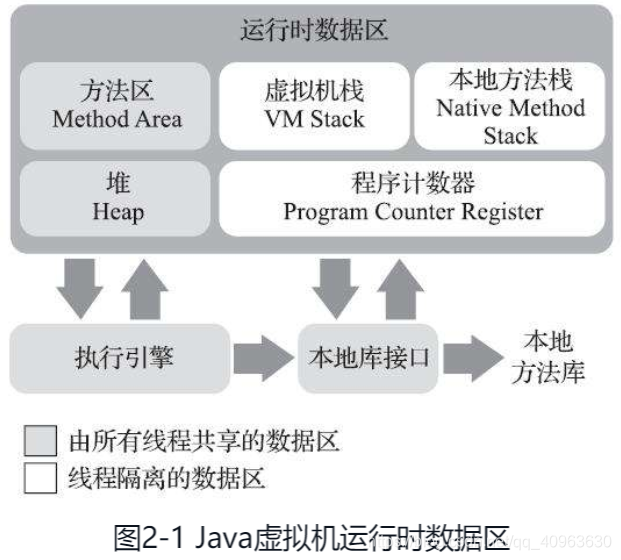
Java虚拟机
文章目录 JVM运行时数据区域HotSpot虚拟机对象探秘实战:OutOfMemoryError异常 JVM 运行时数据区域 HotSpot虚拟机对象探秘 实战:OutOfMemoryError异常...

c++学习 之 函数重载注意事项
文章目录 引用作为函数重载的条件函数重载遇到默认参数 引用作为函数重载的条件 #include <iostream> using namespace std; void fun(int &a) {cout << "void fun(int & a)" << endl; }void fun(const int &a) {cout << "…...

2023-08-27 LeetCode每日一题(合并区间)
2023-08-27每日一题 一、题目编号 56. 合并区间二、题目链接 点击跳转到题目位置 三、题目描述 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组&#…...

C#,数值计算——调适数值积分法(adaptive quadrature)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 调适数值积分法 /// adaptive quadrature /// </summary> public class Adapt { private double x1 { get; } 0.942882415695480; private …...

微信小程序发布迭代版本后如何提示用户强制更新新版本
在点击小程序发布的时候选择,升级选项 之前用户使用过的再打开小程序页面就会弹出升级弹窗modal...
星际争霸之小霸王之小蜜蜂(七)--消失的子弹
目录 前言 一、删除子弹 二、限制子弹数量 三、继续重构代码 总结 前言 昨天我们已经让子弹飞了起来,但是会面临一个和之前小蜜蜂一样的问题,小蜜蜂的行动应该限制在窗口内,那么子弹也是有相同之处,也需要限制一个移动范围&…...
Hadoop入门机安装hadoop
0目录 1.Hadoop入门 2.linux安装hadoop 1.Hadoop入门 定义 Hadoop是一个由Apache基金会所开发的分布式系统基础架构。用户可以在不了解分布式底层细节的情况下,开发分布式程序。充分利用集群的威力进行高速运算和存储。 优势 高可靠性:Hadoop底层维护多…...

cookie技术介绍
title: cookie技术 date: 2023-08-27 21:34:19 tags: [cookie, 网络, http] categories: 网络 我们经常说的cookie缓存数据,允许cookie是什么意思? Cookie也被称作Cookies,它是一种让网站的服务器端可以把少量数据存储在客户端的硬盘或内存中&#x…...

网络摄像头:SparkoCam Crack
SparkoCam 网络摄像头软件 SparkoCam 是一款网络摄像头和视频效果软件,用于广播实时网络摄像头效果并将其应用到视频聊天和录音中。 使用佳能/尼康数码单反相机作为常规网络摄像头通过向实时视频聊天和视频录制添加酷炫的网络摄像头效果和图形来增强 USB 网络摄像…...
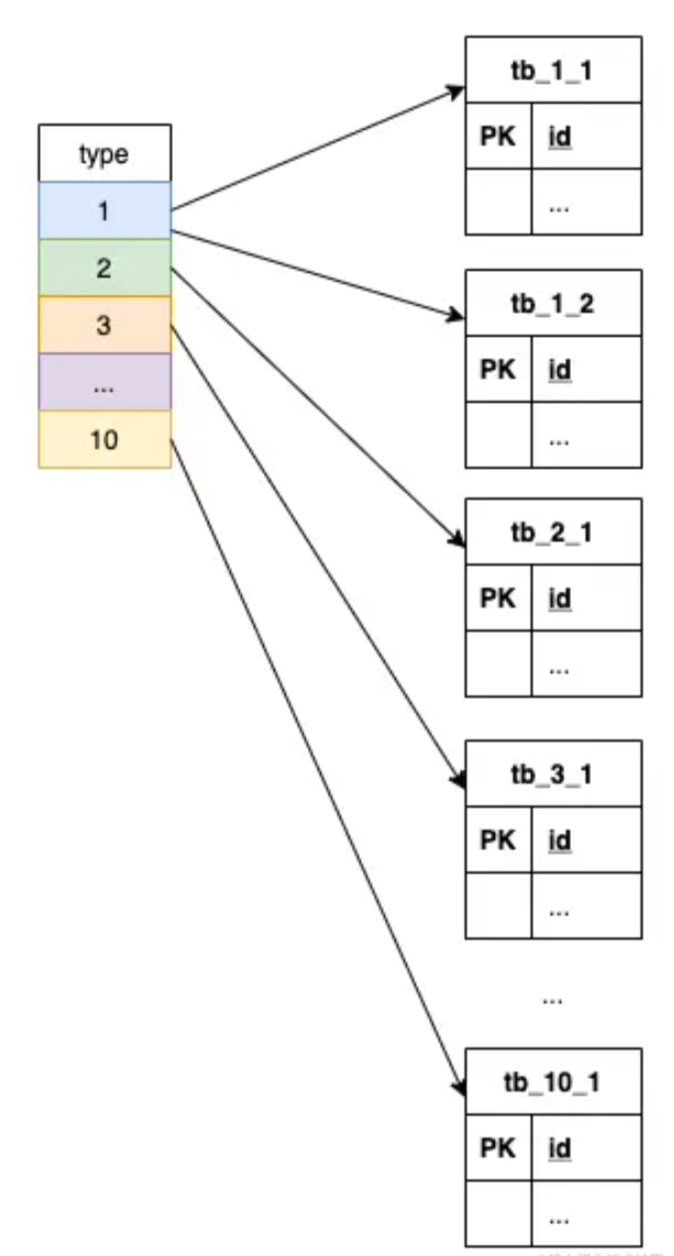
【缓存设计】记一种不错的缓存设计思路
文章目录 前言场景设计思路小结 前言 之前与同事讨论接口性能问题时听他介绍了一种缓存设计思路,觉得不错,做个记录供以后参考。 场景 假设有个以下格式的接口: GET /api?keys{key1,key2,key3,...}&types{1,2,3,...}其中 keys 是业务…...

微信小程序大学校园二手教材与书籍拍卖系统设计与实现
摘 要 随着应用技术的发展以及电子商务平台的崛起,利用线上平台实现的二手交易为传统的二手交易市场注入了新的生机,大学校园内的新生和应届毕业生的相互交替产生了巨大的二手交易空间,同时考虑到环保和资源再利用,大学校园的书籍…...

涛然自得周刊(第06期):韩版苏东坡的突围
作者:何一涛 日期:2023 年 8 月 27 日 涛然自得周刊主要精选作者阅读过的书影音内容,不定期发布。历史周刊内容可以看这里。 电影 兹山鱼谱 讲述丁若铨因政治事件被贬黜到了遥远的黑山岛。来到岛上后,丁被大自然环境疗愈&#…...
DOCKER 部署 webman项目
# 设置基础镜像 FROM php:8.2-fpm# 安装必要的软件包和依赖项 RUN apt-get update && apt-get install -y \nginx \libzip-dev \libpng-dev \libjpeg-dev \libfreetype6-dev \&& rm -rf /var/lib/apt/lists/*# 安装 PHP 扩展 RUN docker-php-ext-configure gd …...
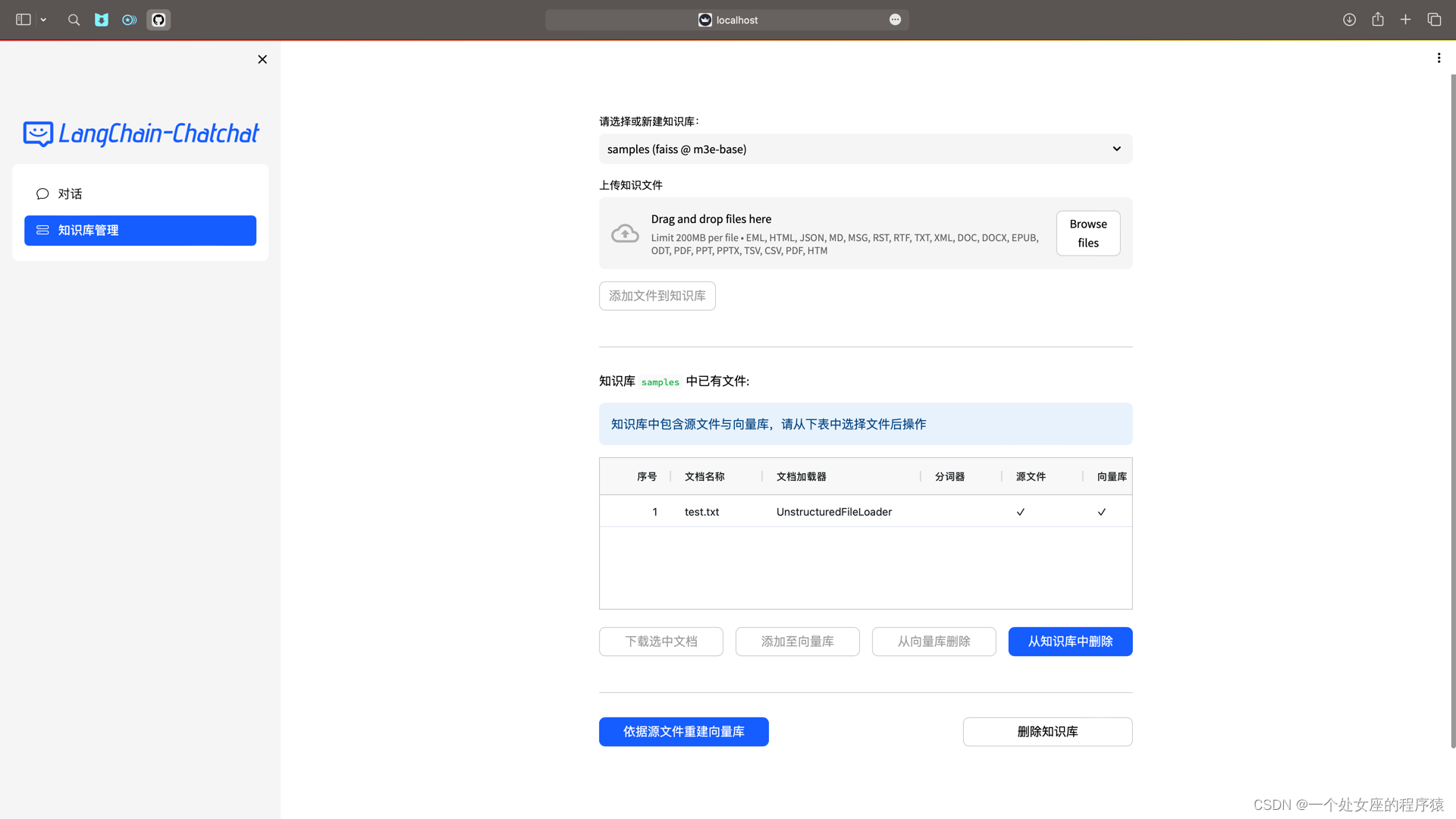
LLMs:LangChain-Chatchat(一款可实现本地知识库问答应用)的简介、安装、使用方法之详细攻略
LLMs:LangChain-Chatchat(一款可实现本地知识库问答应用)的简介、安装、使用方法之详细攻略 目录 LangChain-Chatchat的简介 1、原理图解 2、文档处理实现流程 1、模型支持 (1)、LLM 模型支持 (2)、Embedding 模型支持 LangChain-Chatchat的安装 1、镜像部署…...

Qt 解析XML文件 QXmlStreamReader
如何使用QXmlStreamReader来解析格式良好的XML,Qt的文档中指出,它是一种更快、更方便的Qt自己的SAX解析器(QXmlSimpleReader)的替代,它也较快,在某种情况下,比DOM(QDomDocument&…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
