算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录
- 74. 搜索二维矩阵:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
74. 搜索二维矩阵:
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非递减顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
样例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3输出:true
样例 2:
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13输出:false
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -104 <= matrix[i][j], target <= 104
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 在有序列表中,查找指定元素,一般使用二分查找,非常高效。
- 但是题目中是个二维矩阵,是否还能用二分查找呢?
- 首先想到,可以用两次二分查找,分别看在哪行,再看在哪列,效率已经很高了,但是是否能只用一次二分查找呢?
- 想要使用一次二分查找,就需要将二维矩阵转换成线性结构,有什么办法呢?
- 我们可以快速算出矩阵的长和宽,也就可以拿到它的总长度,我们可以快速将长度范围内的下标,快速转换成行和列的下标,因为行列都是等长的。
题解:
rust:
impl Solution {pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {let (m, n) = (matrix.len(), matrix[0].len());let (mut left, mut right) = (0, m * n);while left < right {let mid = left + ((right - left) >> 1);let v = matrix[mid / n][mid % n];if v < target {left = mid + 1;} else if v > target {right = mid;} else {return true;}}return false;}
}
go:
func searchMatrix(matrix [][]int, target int) bool {m, n := len(matrix), len(matrix[0])i := sort.Search(m*n, func(i int) bool { return matrix[i/n][i%n] >= target })return i < m*n && matrix[i/n][i%n] == target
}
c++:
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {const int m = matrix.size(), n = matrix[0].size();int left = 0, right = m * n;while (left < right) {const int mid = left + ((right - left) >> 1);const int v = matrix[mid / n][mid % n];if (v < target) {left = mid + 1;} else if (v > target) {right = mid;} else {return true;}}return false;}
};
python:
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:m, n = len(matrix), len(matrix[0])left, right = 0, m * nwhile left < right:mid = left + ((right - left) >> 1)v = matrix[mid // n][mid % n]if v < target:left = mid + 1elif v > target:right = midelse:return Truereturn Falsejava:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {final int m = matrix.length, n = matrix[0].length;int left = 0, right = m * n;while (left < right) {final int mid = left + ((right - left) >> 1);final int v = matrix[mid / n][mid % n];if (v < target) {left = mid + 1;} else if (v > target) {right = mid;} else {return true;}}return false;}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:

算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录 74. 搜索二维矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 74. 搜索二维矩阵: 给你一个满足下述两条属性的…...

element浅尝辄止7:InfiniteScroll 无限滚动
滚动加载:滚动至底部时,加载更多数据。 1.如何使用? //在要实现滚动加载的列表上上添加v-infinite-scroll,并赋值相应的加载方法, //可实现滚动到底部时自动执行加载方法。<template><ul class"infinit…...

Day05-Vue基础
Day05-Vue基础 一、单向数据流 父子组件通信。会在父组件中定义好数据,将数据传递给子组件,可以使用这个数据 Vue中针对props这个属性提出了一个单向数据流的概念。 Vue针对props做了一些限制,可以接受值,使用这个值,规范中不要去直接修改这个值 目的是为了对数据流进…...
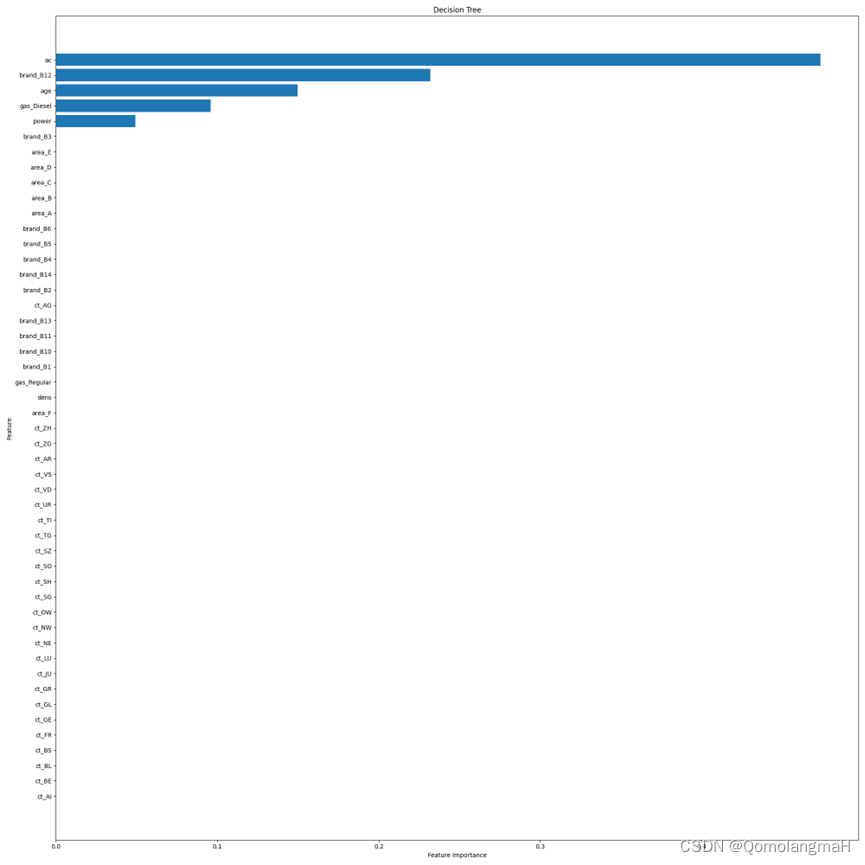
《机器学习在车险定价中的应用》实验报告
目录 一、实验题目 机器学习在车险定价中的应用 二、实验设置 1. 操作系统: 2. IDE: 3. python: 4. 库: 三、实验内容 实验前的猜想: 四、实验结果 1. 数据预处理及数据划分 独热编码处理结果(以…...
14. Docker中实现CI和CD
目录 1、前言 2、什么是CI/CD 3、部署Jenkins 3.1、下载Jenkins 3.2、启动Jenkins 3.3、访问Jenkins页面 4、Jenkins部署一个应用 5、Jenkins实现Docker应用的持续集成和部署 5.1、创建Dockerfile 5.2、集成Jenkins和Docker 6、小结 1、前言 持续集成(CI/CD)是一种…...

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
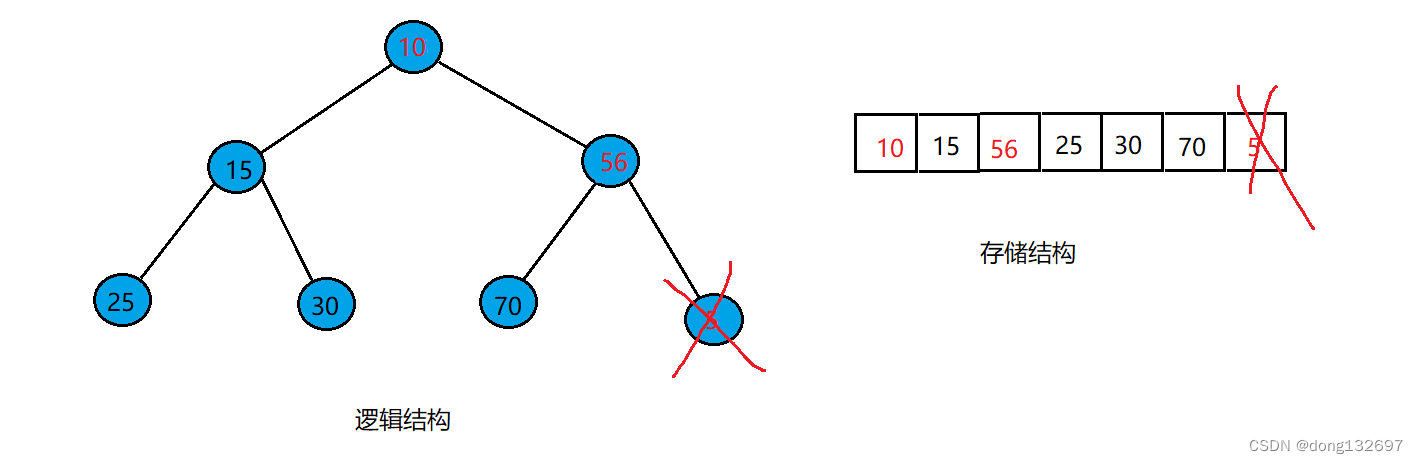
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...
)
前端优化页面加载速度的方法(持续更新)
提速方法方向 延迟脚本加载 使用 async 属性: 在这种方法中,脚本将在下载完成后立即执行,而不会阻塞其他页面资源的加载和渲染。这适用于那些不依赖于其他脚本和页面内容的脚本,例如分析脚本等。示例如下: html …...

利用SSL证书的SNI特性建立自己的爬虫ip服务器
今天我要和大家分享一个关于自建多域名HTTPS爬虫ip服务器的知识,让你的爬虫ip服务器更加强大!无论是用于数据抓取、反爬虫还是网络调试,自建一个支持多个域名的HTTPS爬虫ip服务器都是非常有价值的。本文将详细介绍如何利用SSL证书的SNI&#…...

HTML和CSS
HTML HTML(Hyper Text Markup Language):超文本语言 超文本:超越了文本的限制,比普通文本更强大。除了文字信息,还可以定义图片、音频、视频等内容。 标记语言:由标签构成的语言 HTML标签都是预定义好的。例如:使用&l…...

C#的IndexOf
在 C# 中,IndexOf 是一个字符串、数组或列表的方法,用于查找指定元素的第一个匹配项的索引。它返回一个整数值,表示匹配项在集合中的位置,如果未找到匹配项,则返回 -1。 IndexOf 方法有多个重载形式,可以根…...

深度学习2.神经网络、机器学习、人工智能
目录 深度学习、神经网络、机器学习、人工智能的关系 大白话解释深度学习 传统机器学习 VS 深度学习 深度学习的优缺点 4种典型的深度学习算法 卷积神经网络 – CNN 循环神经网络 – RNN 生成对抗网络 – GANs 深度强化学习 – RL 总结 深度学习 深度学习、神经网络…...

利用LLM模型微调的短课程;钉钉宣布开放智能化底座能力
🦉 AI新闻 🚀 钉钉宣布开放智能化底座能力AI PaaS,推动企业数智化转型发展 摘要:钉钉在生态大会上宣布开放智能化底座能力AI PaaS,与生态伙伴探寻企业服务的新发展道路。AI PaaS结合5G、云计算和人工智能技术的普及和…...
 UML之用例图详解)
软件工程(七) UML之用例图详解
1、UML-4+1视图 UML-4+1视图将会与后面的架构4+1视图会一一对应上 视图往往出现在什么场景:我们看待一个事物,我们觉得它很复杂,难以搞清楚,为了化繁为简,我们会从一个侧面去看,这就是视图。而4+1视图就是分不同角度去看事物。 逻辑视图(logical view) 一般使用类与对…...
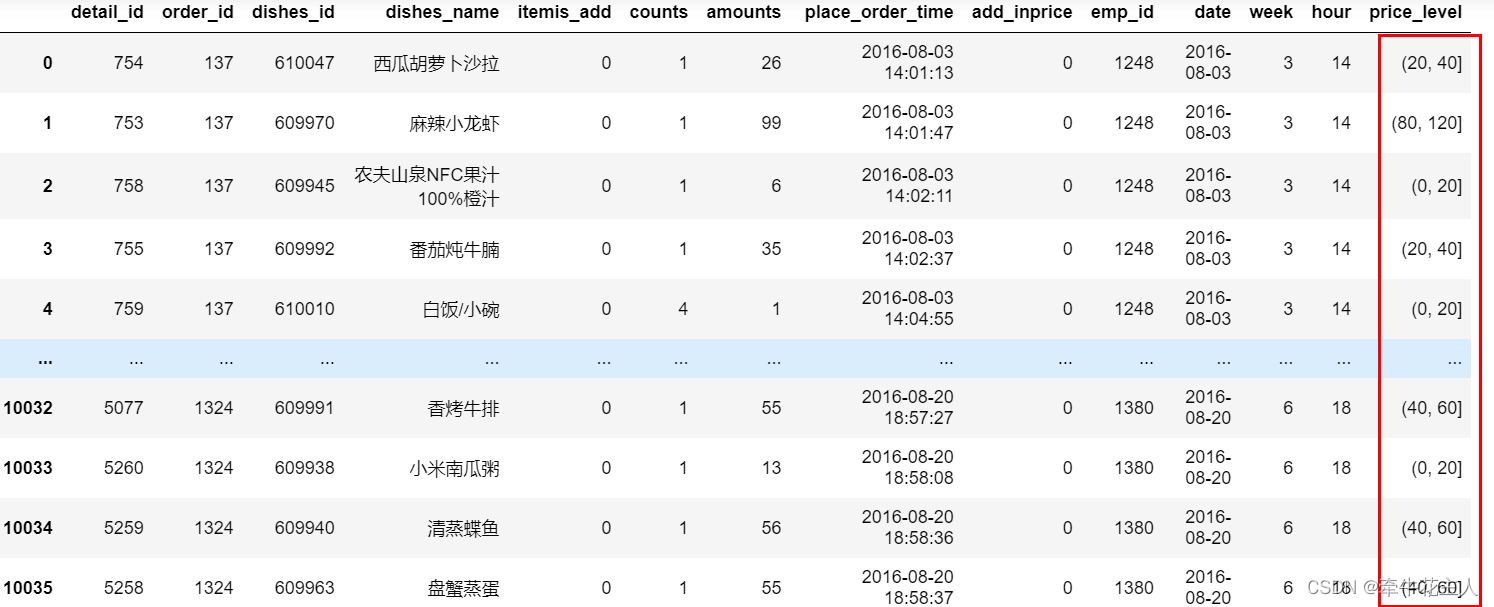
pd.cut()函数--Pandas
1. 函数功能 将连续性数值进行离散化处理:如对年龄、消费金额等进行分组 2. 函数语法 pandas.cut(x, bins, rightTrue, labelsNone, retbinsFalse, precision3, include_lowestFalse, duplicatesraise, orderedTrue)3. 函数参数 参数含义x要离散分箱操作的数组&…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
