BM20 数组中的逆序对
描述

解题思路:归并排序
分治:分治即“分而治之”,“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题,子问题继续按照这样划分,直到问题可以被轻易解决;“治”指的是将子问题单独进行处理。经过分治后的子问题,需要将解进行合并才能得到原问题的解,因此整个分治过程经常用递归来实现。
具体做法:
1、这里要借助一个辅助数组,用来暂时存储合并后的结果。然后就开始进入划分阶段,把原数组从中间分开,直到子数组长度为1。
2、使用归并排序对原数组进行排序,并且统计逆序对,在这里设置两个指针i,j分别在左右子区间上移动,此时左区间的下标i都是小于右区间的,若知道了第一个大于a[j]的数,设为a[i],则左区间中a[i]以后的所有数,都比a[j]大。故此时,在左区间中,与a[j]构成逆序对的数字个数为左边剩下的数,剩余的数=(右端-左端+1)=(mid-i+1)。这个就是逆序对的计算方法。
3、将排好序的子序列合并,同时累加逆序对。
图解:
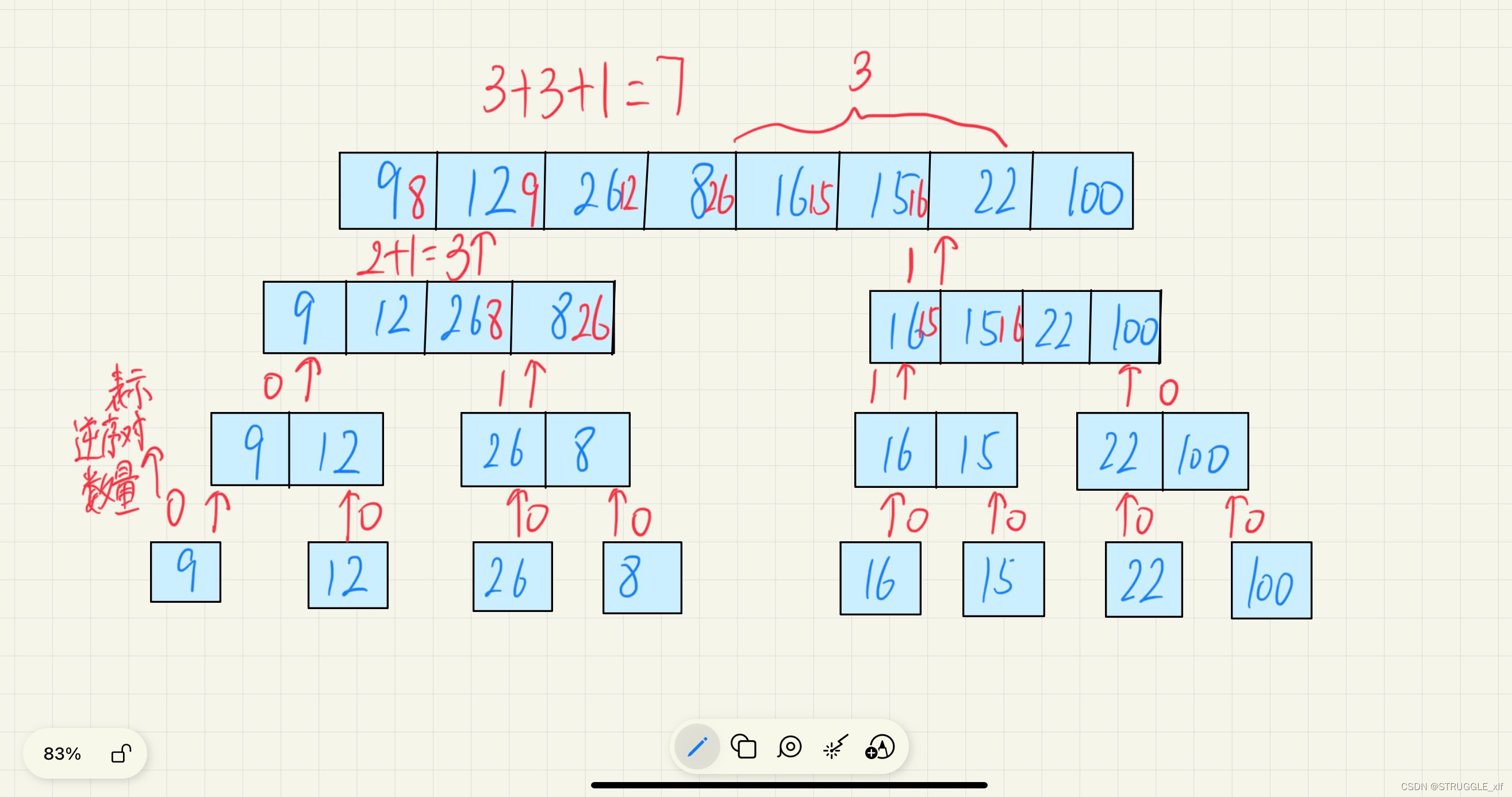
代码:
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param nums int整型一维数组 * @return int整型*/public int mod = 1000000007;public int mergeSort(int left,int right,int [] data,int[] temp){if(left>=right){return 0;}int mid = (left+right)/2;int res = mergeSort(left,mid,data,temp)+mergeSort(mid+1,right,data,temp);res %= mod;//i,j代表两个指针,分别在左右子区间上移动。int i = left,j = mid+1;for(int k=left;k<=right;k++){temp[k] = data[k]; //temp为辅助数组}for(int k=left;k<=right;k++){if(i==mid+1){ //如果左边有剩余,不太懂这处代码data[k] = temp[j++];}//如果右边有剩余,或者左边数更小else if(j==right+1||temp[i]<=temp[j]){ data[k] = temp[i++];//不太懂处代码}else{data[k] = temp[j++];//逆序对计算方法res += mid-i+1;}}return res%mod;}public int InversePairs (int[] nums) {// write code hereint n = nums.length;int [] res = new int[n];return mergeSort(0,n-1,nums,res);}
}
个人疑问:不知道有没有和我一样的小伙伴,在看这道题的解题思路会有这样的疑问:为什么可以排序呢?这里题目要求的是在一个已经列好的数组中左边的数大于右边,才被称为逆序数,而如果使用归并排序的话,这个数组不是都有序了吗,有序的基础上找逆序,不是和题目违背了吗?
经过思考,我个人的见解是这样的,这里归并排序计算逆序对的数量和暴力解法不一样,暴力解法是在一个已有的数组中,对于每一个数,都判断其他的数是否比该数大,而递归排序,它比较的不是相邻的两个数,而是相邻的两个子数组,我认为这是看懂这道题的关键,因为比较的是两个子数组,所以在两个子数组中已经排好序是没关系的,因为两个子数组的相对顺序没有变,所以如果在左区间发现了一个比右区间大的数,那么说明左区间中这个数以后的数都会比右区间大,这是递归算法计算的公式。
相关文章:

BM20 数组中的逆序对
描述 解题思路:归并排序 分治:分治即“分而治之”,“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题,子问题继续按照这样划分,直到问题可以被轻易解决;“治”指的是将子问题单独进…...

高德猎鹰轨迹查询相关接口
高德猎鹰轨迹官网:服务管理-API文档-开发指南-猎鹰轨迹服务 | 高德地图API 轨迹查询 httpclient的post // post方法请求 创建轨迹 private static void createTrace() {String key "高德注册的key";String sid "服务id"; // 服务idString…...

整理总结新手开始抖音小店经营:常见问题及解决办法
抖音小店作为一种新兴的电商模式,在短时间内获得了广泛的关注和使用。然而,对于新手来说,抖音小店经营可能会遇到一些问题。下面是四川不若与众总结的一些常见的问题以及相应的解决办法。 问题一:产品选择困难 对于新手来说&#…...
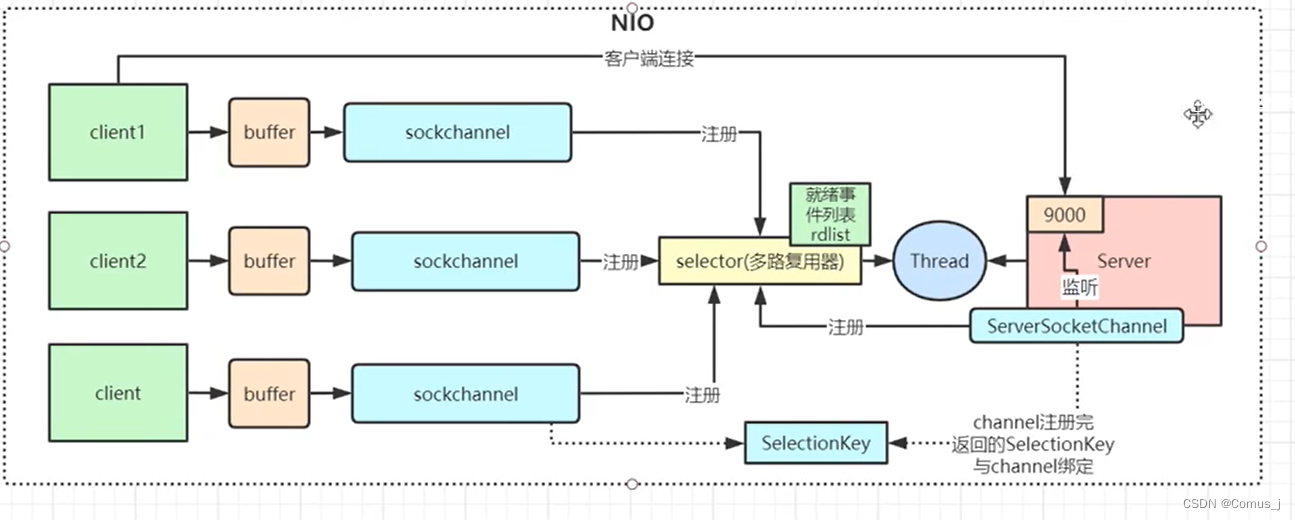
4-1-netty
非阻塞io 服务端就一个线程,可以处理无数个连接 收到所有的连接都放到集合channelList里面 selector是有事件集合的 对server来说优先关注连接事件 遍历连接事件...

hive 动态分区-动态分区数量太多也会导致效率下降只设置非严格模式也能执行动态分区
hive 动态分区-动态分区数量太多也会导致效率下降&只设置非严格模式也能执行动态分区 结论 在非严格模式下不开启动态分区的功能的参数(配置如下),同样也能进行动态分区数据写入,目测原因是不严格检查SQL中是否指定分区或者…...
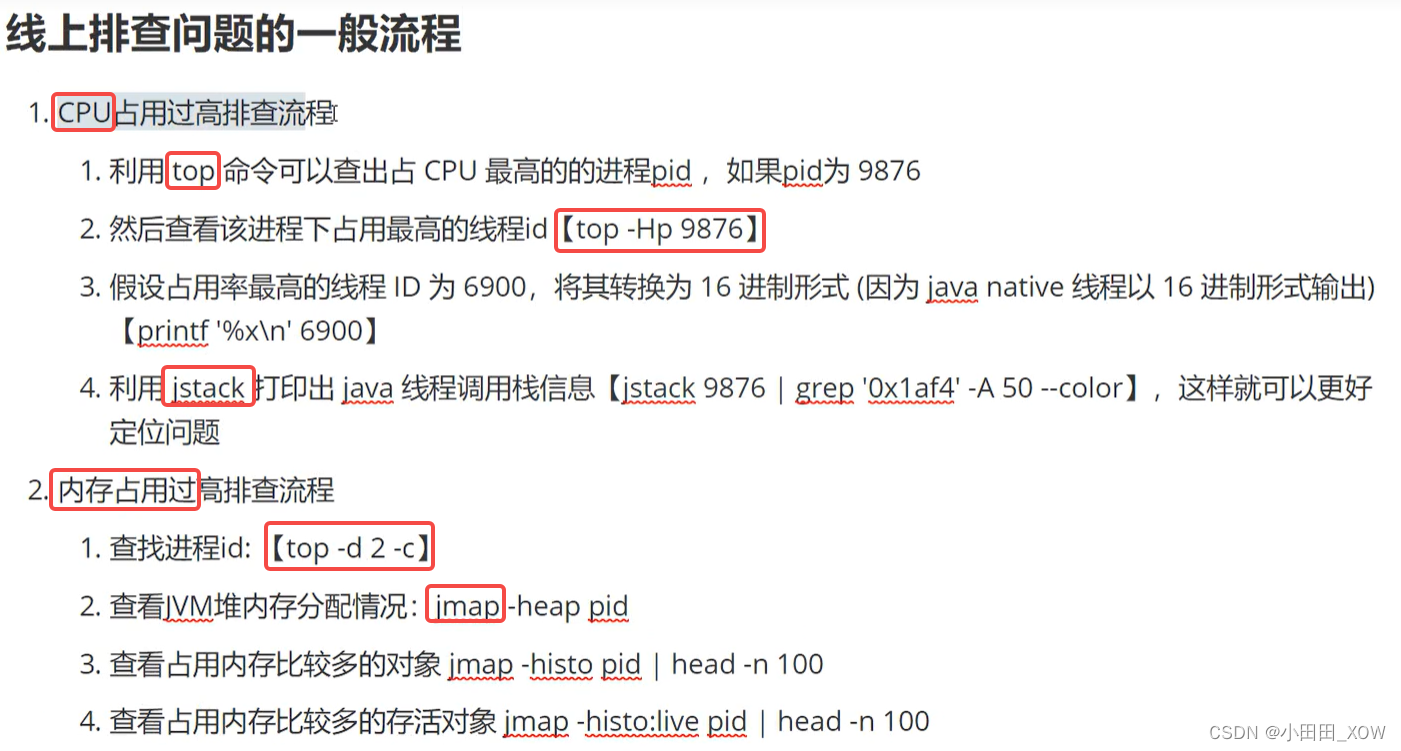
java八股文面试[JVM]——JVM调优
知识来源: 【2023年面试】JVM性能调优实战_哔哩哔哩_bilibili...

FairyGUI-Unity 异形屏适配
本文中会修改到FairyGUI源代码,涉及两个文件Stage和StageCamera,需要对Unity的屏幕类了解。 在网上查找有很多的异形屏适配操作,但对于FairyGUI相关的描述操作很少,这里我贴出一下自己在实际应用中的异形屏UI适配操作。 原理 获…...
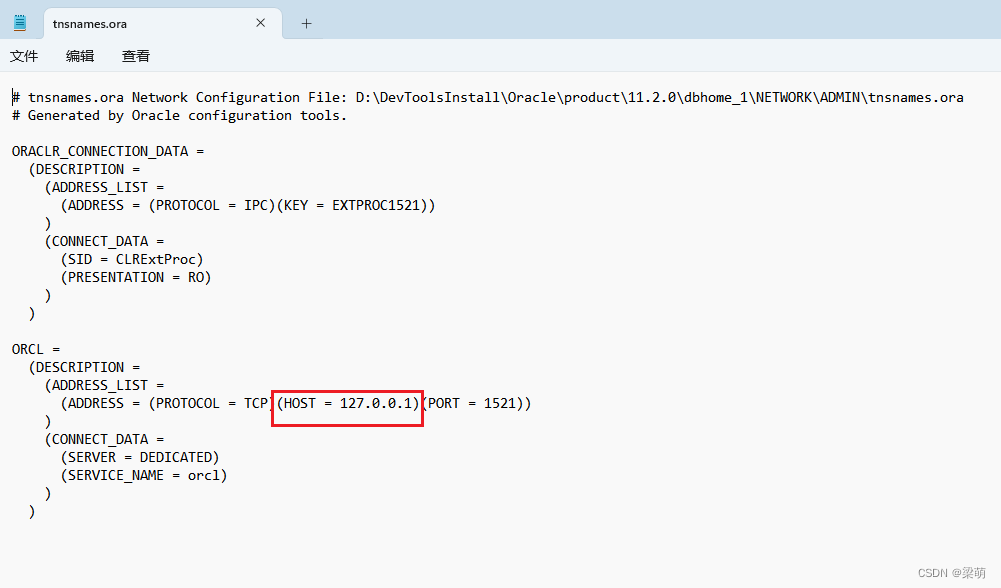
Oracle监听器启动出错:本地计算机上的OracleOraDb11g_home1TNSListener服务启动后又停止了解决方案
在启动oracle的服务OracleOraDb11g_home1TNSListener时,提示服务启动后又停止了。 解决方法: 修改oracle安装目录下的两个配置文件: 以上两个文件,对应的HOST的值,都改为127.0.0.1 然后再启动服务,启动成…...
<context:annotation-config/>的作用)
Spring复习:(58)<context:annotation-config/>的作用
引入如下的BeanPostProcessor • ConfigurationClassPostProcessor • AutowiredAnnotationBeanPostProcessor • CommonAnnotationBeanPostProcessor • PersistenceAnnotationBeanPostProcessor • EventListenerMethodProcessor如果xml文件配置了bean中使用了Autowired注解…...

“东方杯”英特尔oneAPI黑客松大赛—参赛经验分享
目录 前言1、大赛要求2、oneMKL介绍3、准备 oneMKL基本使用1、下载:2、安装:3、初始化oneMKL环境:4、编译代码5、运行 所需的头文件使用oneMKL工具生成随机数使用fftw3计算FFT调用oneMKL API加速计算FFT对比两种方法的准确性输出结果结束语 前…...
win10家庭版远程桌面补丁_rdp wrapper
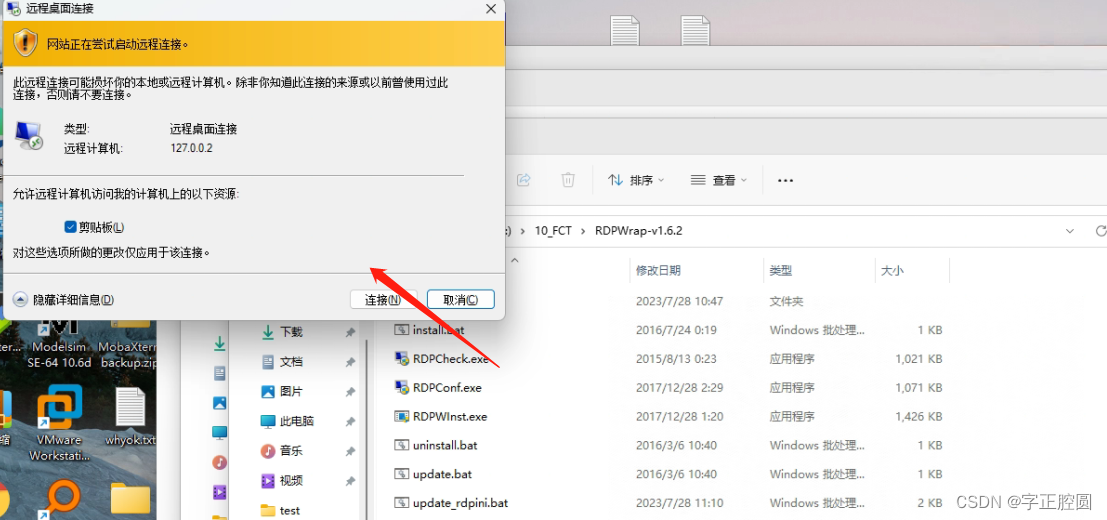
RDP Wrapper Library 就是可以帮你在 Windows 7、Windows 8、Windows 10 家庭版中打开远程桌面的工具。 1、把电脑上打开的安全软件与杀毒软件都关掉,因为这个远程桌面补丁会修改系统文件,所以安全软件可能会拦截。 2、下载RDP Wrapper Library补丁压缩…...

【C++设计模式】开放-封闭原则
2023年8月27日,周日下午 我觉得我的这篇博客还是写得很不错的,哈哈哈。 目录 概述举例说明用开放-封闭原则重构 概述 开放-封闭原则(Open-Closed Principle,OCP)是面向对象设计中的一个重要原则,也是许多…...

vue+file-saver+xlsx+htmlToPdf+jspdf实现本地导出PDF和Excel
页面效果如下(echarts图表按需添加,以下代码中没有) 1、安装插件 npm install xlsx --save npm install file-saver --save npm install html2canvas --save npm install jspdf --save2、main.js引入html2canvas import htmlToPdf from …...
axios 进阶
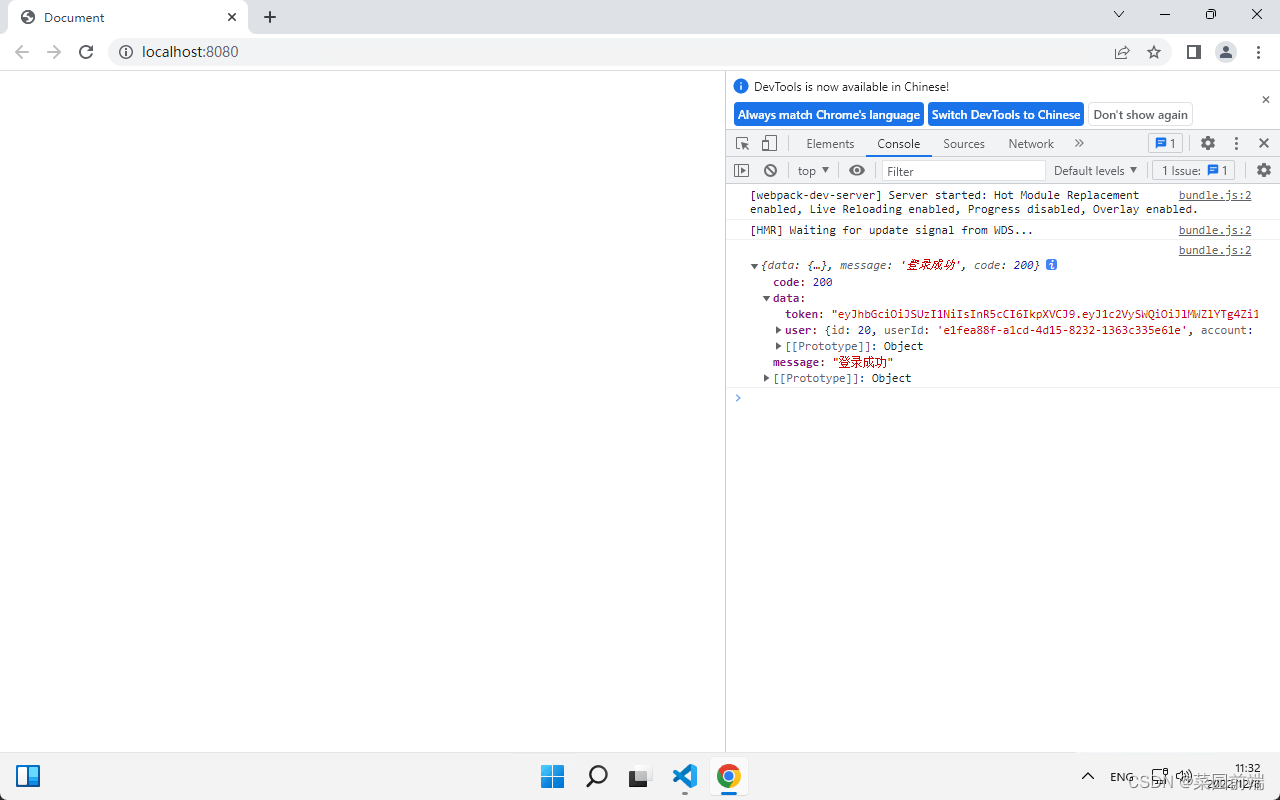
axios 进阶 接口传参方式 使用 xhr 原生技术或者是 axios 时,它的 post 传参方式是键值对的形式 keyvalue。但是在实际开发中一般是使用对象的形式定义数据,方便读取和赋值。所以当我们需要发起请求时可以通过 qs 这一款插件将对象转成键值对形式&…...

Redis限流实践:实现用户消息推送每天最多通知2次的功能
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师…...

uniapp 存储base64资源为http链接图片
1. 新建一个base64.js 文件 const fsm wx.getFileSystemManager(); // base64data base64资源 // name 文件名 function base64src(base64data, name, cb) {const time new Date().getTime();const filePath ${wx.env.USER_DATA_PATH}/${name}.${time}.png;const buffer …...

列表类控件虚拟化
WPF列表控件提供的最重要的功能是UI虚拟化(WPF编程宝典说的)。所有的WPF列表控件(所有继承自ItemsControl的控件,包括ListBox、CombBox、ListView、TreeView、DataGrid)都支持UI虚拟化。 UI虚拟化的支持实际上没有被构…...

c# 多线程Task.Run 取消正在执行的多线程
c# 异步处理,上次处理没有完成,下次有紧接着处理多线程出错 在 C# 中进行异步处理时,确保处理上一个任务完成后再处理下一个任务是很重要的,特别是在涉及多线程的情况下。如果上一个任务尚未完成,而下一个任务又开始执…...

sql server 如何设置主键
开始之前 限制和局限 一个表只能包含一个 PRIMARY KEY 约束。 在 PRIMARY KEY 约束中定义的所有列都必须定义为 NOT NULL。 如果没有指定为 Null 性,则加入 PRIMARY KEY 约束的所有列的为 Null 性都将设置为 NOT NULL。 创建主键会自动创建相应的唯一群集索引、…...
【LeetCode-中等题】19. 删除链表的倒数第 N 个结点
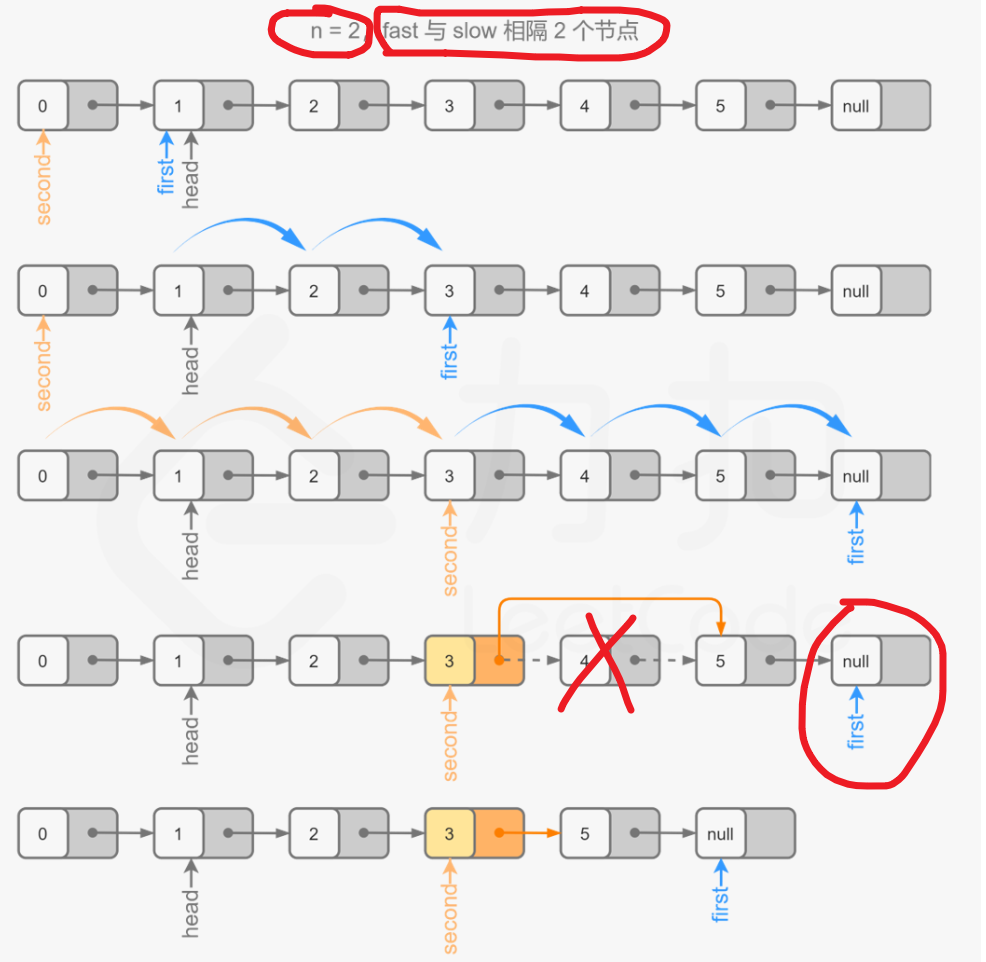
文章目录 题目方法一:节点加入集合找索引方法二:直接计算长度,然后找出要删除的节点的前一个节点方法三:栈方法四:前后双指针 题目 这题的关键在与两个点 一定要设置一个哑结点,防止删除第一个元素时,导致空…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
