【题解】JZOJ6578 / 洛谷P5201[USACO2019Jan]Shortcut G
洛谷 P5201 [USACO19JAN] Shortcut G
题意
在一个带权无向连通图上,每个点有 a i a_i ai 只奶牛,奶牛会走最短路径到 1 1 1,如果有多条路径,选择字典序最小的,定义移动总时间为所有奶牛走到 1 1 1 的时间之和。你可以修建一条从任意一点到 1 1 1 的边权为 t t t 的边,奶牛只有在平时走到 1 1 1 的路上看到这条边才会走。求最多能减少多少移动总时间。
题解
题目保证了对于每个点都有唯一的路径走到 1 1 1,那么可以建出一棵树,根节点为 1 1 1。
然后统计一下子树中奶牛数量总和,对于每个点尝试建时间为 t t t 的新边,可以 O ( 1 ) O(1) O(1) 求出减少的移动总时间。设 j j j 为 i i i 的子树中的节点,则减少的时间为 ( d i s i − t ) ∑ j a j (dis_i-t)\sum\limits_{j}a_j (disi−t)j∑aj。
时间复杂度 O ( n ) O(n) O(n)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50005;
int n, m, t, a[N], vis[N];
LL dis[N], cnt[N], ans = 0;
int cn1 = 0, fi1[N], nx1[N << 1], to1[N << 1], va1[N << 1], cn2 = 0, fi2[N], nx2[N << 1], to2[N << 1];
void ad1(int u, int v, int w) {cn1++, nx1[cn1] = fi1[u], fi1[u] = cn1, to1[cn1] = v, va1[cn1] = w; cn1++, nx1[cn1] = fi1[v], fi1[v] = cn1, to1[cn1] = u, va1[cn1] = w;
}
void ad2(int u, int v) { cn2++, nx2[cn2] = fi2[u], fi2[u] = cn2, to2[cn2] = v; }
struct node {int r;LL dis;bool operator < (const node &T) const { return dis > T.dis; }
};
priority_queue<node> pq;
void dij(int r) {memset(dis, 0x3f, sizeof(dis)), dis[r] = 0;pq.push((node){r, 0});while (!pq.empty()) {node h = pq.top();pq.pop();if (vis[h.r]) continue;vis[h.r] = 1;for (int i = fi1[h.r]; i; i = nx1[i])if (dis[to1[i]] > dis[h.r] + va1[i])dis[to1[i]] = dis[h.r] + va1[i], pq.push((node){to1[i], dis[to1[i]]});}
}
void dfs(int r) {cnt[r] = a[r];for (int i = fi2[r]; i; i = nx2[i]) dfs(to2[i]);for (int i = fi2[r]; i; i = nx2[i]) cnt[r] += cnt[to2[i]];if (t < dis[r]) ans = max(ans, (dis[r] - t) * cnt[r]);
}
int main() {scanf("%d%d%d", &n, &m, &t);for (int i = 1; i <= n; i++) scanf("%d", &a[i]);for (int i = 1, u, v, w; i <= m; i++) scanf("%d%d%d", &u, &v, &w), ad1(u, v, w);dij(1);for (int i = 2; i <= n; i++) {int x = n;for (int j = fi1[i]; j; j = nx1[j])if (dis[i] == dis[to1[j]] + va1[j])x = min(x, to1[j]);ad2(x, i);}dfs(1);printf("%lld", ans);return 0;
}
相关文章:

【题解】JZOJ6578 / 洛谷P5201[USACO2019Jan]Shortcut G
洛谷 P5201 [USACO19JAN] Shortcut G 题意 在一个带权无向连通图上,每个点有 a i a_i ai 只奶牛,奶牛会走最短路径到 1 1 1,如果有多条路径,选择字典序最小的,定义移动总时间为所有奶牛走到 1 1 1 的时间之和。…...
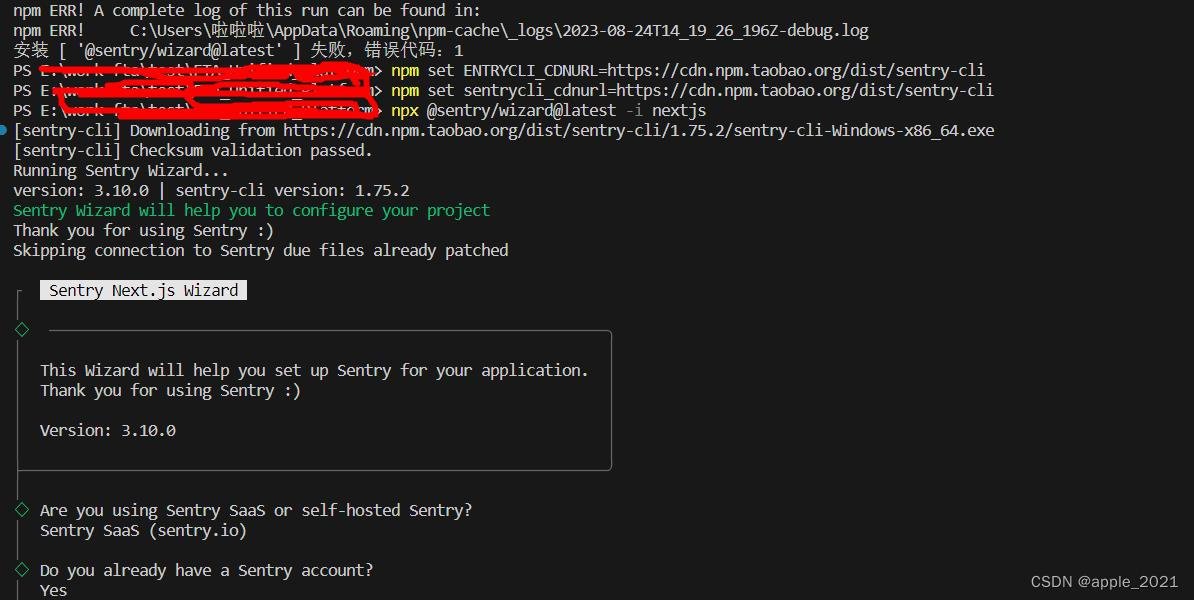
npm install sentry-cli失败的问题
1. 目前报错 2. 终端运行 npm set ENTRYCLI_CDNURLhttps://cdn.npm.taobao.org/dist/sentry-cli npm set sentrycli_cdnurlhttps://cdn.npm.taobao.org/dist/sentry-cli3. 再安装 npx sentry/wizardlatest -i nextjs即可成功...

Node opensslErrorStack 错误解决方法记录
从Git仓库中下载了一个老项目,使用npm install 安装后没有问题,当我使用npm run dev 的时候遇到了 OpenSSL 相关错误,例如 opensslErrorStack: [error:03000086:digital envelope routines::initialization error] 网上找了一下相关信息&am…...

你知道什么是Grandmillennial风格吗,进来看看吧
如果你既欣赏祖母的印花棉布扶手椅和大胆的图案,又喜欢千禧一代朋友现代家居中的开放空间和时尚家具,那么 "千禧一代 “风格就是为你量身打造的。它借鉴了几十年来的流行趋势,形成了一种独特的、带有现代风格的老式设计。 在典型的 &quo…...

App Inventor 2 开发 ChatGPT 对话App
ChatGPT大家应该不会陌生,它的回答内容非常的专业及深入,具有实际的可指导性。我们通过App Inventor 2开发一个简单的对话App,先看效果: App Inventor 2 ChatGPT教育领域对话演示 代码块如下: 用到的核心组件“ChatBot…...

SQL 大小敏感问题
在SQL中,关键字和函数名 是不区分 大小写的 比如(select、where、order by 、group by update 等关键字),以及函数(ABS、MOD、round、min等) window系统默认是大小写不敏感 (ZEN文件和zen 文件 不能同时存在ÿ…...

微信小程序+Taro 混编,Taro 使用微信原生 behaviors
最近有一个小程序项目,因为一些原因项目架构选择了微信小程序原生Taro 混编的方式进行开发,在开发的过程中发现 Taro 不支持使用原生的 behaviors 特性,因为混编的原因项目当中已有原生页面在使用 behaviors,所以需要一个方案在不…...
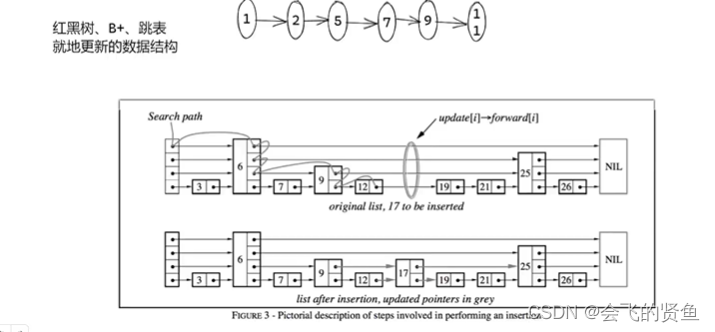
b树/b+树、时间轮、跳表、LSM-Tree
b树、b树:关系型数据库核心存储结构 1、为什么磁盘数据存储结构用B树、而不用红黑树 磁盘每次读取不是读一个节点、是返回一页数据。 红黑树每次遍历一个节点排除一半数据。 B树通常映射相邻的磁盘页数据。4K mysql索引一个节点隐射16k故而映射4倍,故…...
Unity OnDrawGizmos的简单应用 绘制圆形
编辑器和配置表各有各的好。 卡牌游戏即使再复杂,哪怕是梦幻西游,大话西游那种,甚至wow那种,用配表都完全没问题。但是崩坏3,或者鬼泣,格斗游戏,可视化编辑器是唯一的选择。 开发初期刚开始配技…...
uniapp语法3)
Uniapp笔记(四)uniapp语法3
一、商品详情 1、从商品列表页跳转到商品详情页 在商品列表的项中绑定单击事件,并传递商品id值 <view class"goods-item" v-for"(item,index) in goodsList" :key"index" click"goGoodsDetail(item.goods_id)"> &…...

leetcode做题笔记105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 思路一:递归 struct TreeNode* buildTree(int* preorder, int preorderSize, int* ino…...

Python里的列表List求和
1、使用sum()函数 numbers [1, 2, 3, 4, 5] total sum(numbers) print(total) # 输出 15 2、注意事项 在使用 sum() 函数获取列表的总和时,需要注意以下几点: sum() 函数只能用于数字类型的可迭代对象,如果 iterable 中包含了非数字类…...
)
启动docker容器的几种方法和注意事项(docker-compose,dockerfile)
1:要启动容器必须都先创建好镜像文件 C:\Users\dell>docker images REPOSITORY TAG IMAGE ID CREATED SIZE poi 1.0 22738bb31074 4 hours ago 105MB redis latest 506734eb5e71 6 days ago 138MB ng…...
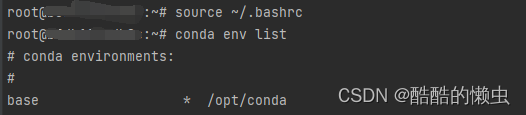
bash: conda: command not found
问题描述: 在Pycharm上用SSH远程连接到服务器,打开Terminal准备查看用 conda 创建的虚拟环境时,却发现调用 conda 指令时出现以下报错: -bash: conda: command not found如果使用Xshell 利用端口号直接连接该 docker 容器&#…...
Leetcode-每日一题【剑指 Offer 36. 二叉搜索树与双向链表】
题目 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。 为了让您更好地理解问题,以下面的二叉搜索树为例: 我们希望将这个二叉搜索树转化为双向循环链表…...
ctfshow-萌新专属红包题
0x00 前言 CTF 加解密合集CTF Web合集 0x01 题目 0x02 Write Up 访问之后是一个登录页面,扫了目录,试了sql注入,没办法于是跑一跑弱口令,所以有事没事,admin弱口令跑一跑 搜索 微信公众号 皓月当空w 发送关键字 字典…...
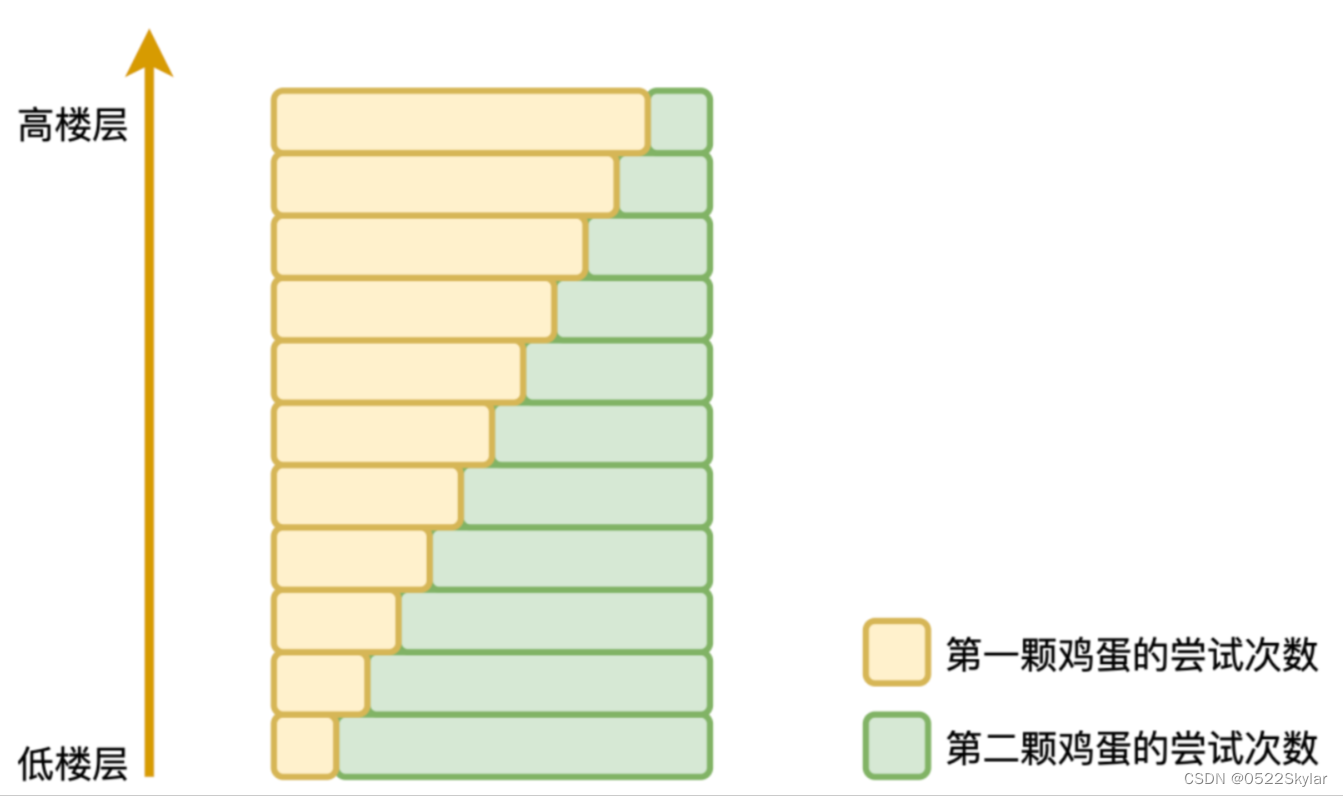
谷歌面试-扔鸡蛋
今天想跟大家分享一个有意思的面试题,这让我再一次感叹思维的奇妙,接下来我们一起看看吧~ 首先来看看题目: 你有2颗鸡蛋,需要以最少的尝试次数来判断在100层的高楼上,哪一层楼是鸡蛋的安全层。 换句话说,…...
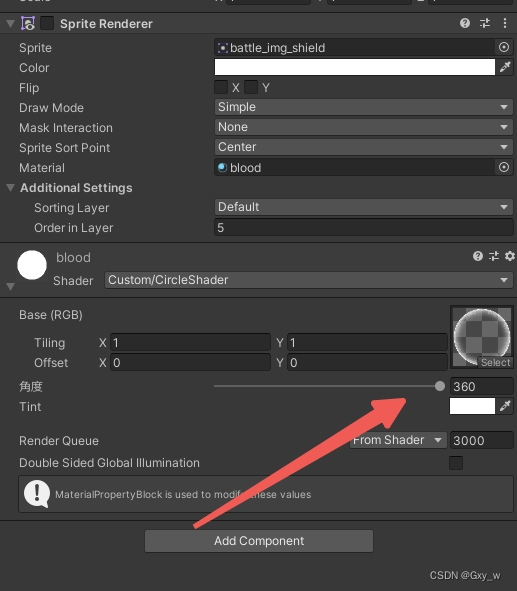
Unity血条制作
一、使用UGUI制作血条 我一般使用image制作血条,当然,也可以使用滑动组件Slider。image的具体操作步骤如下 普通血条 1、在Hierarchy面板中,创建两个image组件,将其中一个设置为另外一个的子节点 2、在Inspector面板中&#…...

vue,uniapp生成二维码
话不多说直接开干 先是vue的 1,首先按照一下依赖 npm install --save qrcode 2,在需要使用的页面引入 import QRCode from qrcode; 3,使用 const codeDetail (item) > {//这个item.code是要生成的数据,我的是一串数字QRCode.toDataURL(item.co…...
分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测
分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测 目录 分类预测 | MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SSA-CNN-SVM基于麻雀算法优化卷积支持向量机分类预测…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
