回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)
目录
- 回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)
- 效果一览
- 基本介绍
- 程序设计
- 参考资料
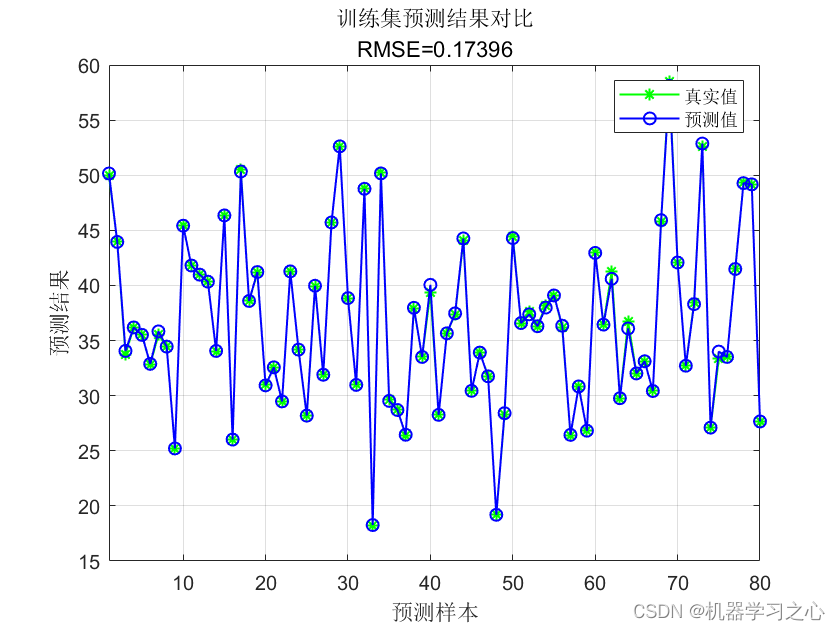
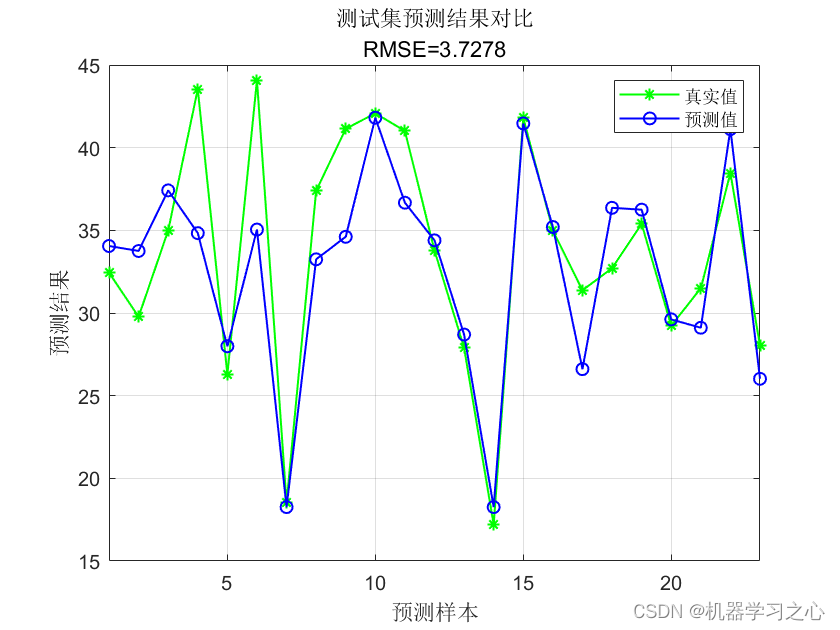
效果一览

基本介绍
回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图),输入多个特征,输出单个变量,多输入单输出回归预测;
多指标评价,代码质量极高;excel数据,方便替换,运行环境2018及以上。
布谷鸟算法(Cuckoo Search Algorithm)是一种基于自然界布谷鸟繁殖行为的优化算法,用于解决优化问题。布谷鸟算法可以与极限学习机(Extreme Learning Machine,ELM)结合,以优化极限学习机的性能。通过将布谷鸟算法应用于极限学习机的优化过程,可以帮助寻找更好的超参数组合,以提高极限学习机在特定问题上的性能和泛化能力。
程序设计
- 完整源码和数据获取方式:私信回复CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)。
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行%% 导入数据
res = xlsread('data.xlsx');%% 划分训练集和测试集
temp = randperm(103);P_train = res(temp(1: 80), 1: 7)';
T_train = res(temp(1: 80), 8)';
M = size(P_train, 2);P_test = res(temp(81: end), 1: 7)';
T_test = res(temp(81: end), 8)';
N = size(P_test, 2);%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);%% 仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test);%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);%% 相关指标计算
% 决定系数 R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;disp(['训练集数据的R2为:', num2str(R1)])
disp(['测试集数据的R2为:', num2str(R2)])% 平均绝对误差 MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 - T_test )) ./ N ;disp(['训练集数据的MAE为:', num2str(mae1)])
disp(['测试集数据的MAE为:', num2str(mae2)])% 平均相对误差 MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 - T_test ) ./ N ;disp(['训练集数据的MBE为:', num2str(mbe1)])
disp(['测试集数据的MBE为:', num2str(mbe2)])
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718
相关文章:

回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现CSO-ELM布谷鸟算法优化极限学习机多输入单输出回归预测(多指标,多图)效果一览基本介…...

静态链接库和动态链接库的区别
C静态链接库(Static Linking)和动态链接库(Dynamic Linking)的主要区别在于代码的组织和加载方式。 静态链接库 在编译时将库的代码和应用程序的代码合并在一起,生成一个单独的可执行文件。执行文件独立包含所需的库…...

使用 python 源码搭建 conda 环境
今天需要使用 python 2.6.8 的环境,发现 conda 设置成清华源后,没有旧版本了。所以打算从官网上下载一份 python 进行安装, 结果发现,conda 不能直接安装离线包(也可能我没找到方法),经过一番尝…...

dart 学习之 异步操作
import package:dio/dio.dart;// 定义一个异步函数,用于获取 URL 的内容 Future<String> getUrl(String url) async {Dio dio Dio();Response response await dio.get(url);return response.data; }void main() async {// 在主函数中执行异步操作var conten…...
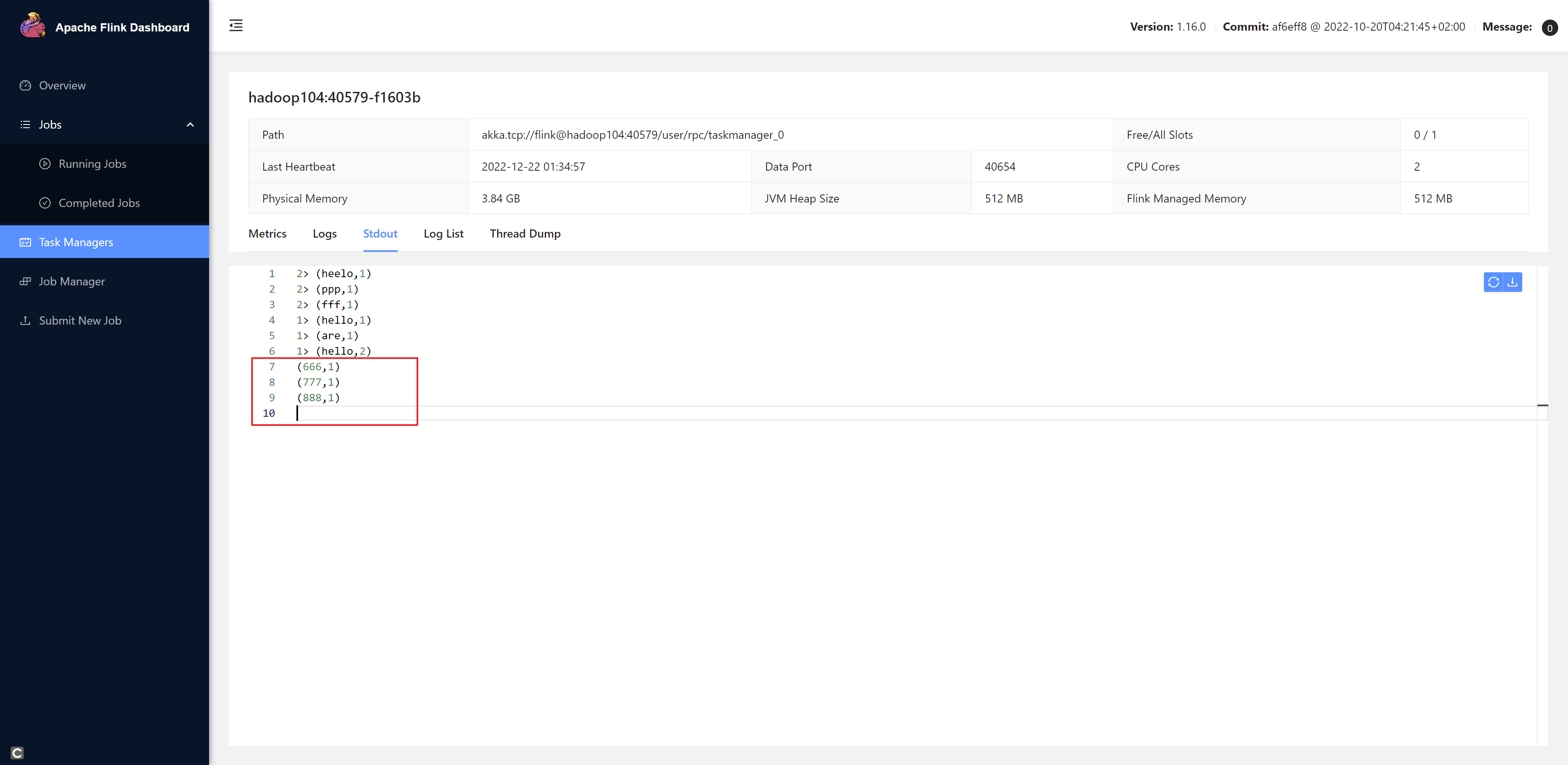
《Flink学习笔记》——第二章 Flink的安装和启动、以及应用开发和提交
介绍Flink的安装、启动以及如何进行Flink程序的开发,如何运行部署Flink程序等 2.1 Flink的安装和启动 本地安装指的是单机模式 0、前期准备 java8或者java11(官方推荐11)下载Flink安装包 https://flink.apache.org/zh/downloads/hadoop&a…...
网易新财报:游戏稳、有道进、云音乐正爬坡
今年以来,AI大模型的火热程度屡屡攀升,越来越多的企业都加入到了AI大模型的赛场中,纷纷下场布局。而在众多参与者中,互联网企业的身影更是频频浮现,比如,百度、阿里巴巴、腾讯等等。值得一提的是࿰…...
Docsify的评论系统gitalk配置过程
💖 作者简介:大家好,我是Zeeland,开源建设者与全栈领域优质创作者。📝 CSDN主页:Zeeland🔥📣 我的博客:Zeeland📚 Github主页: Undertone0809 (Zeeland)&…...
卡片开发应用上下文Context使用场景二)
HarmonyOS/OpenHarmony(Stage模型)卡片开发应用上下文Context使用场景二
3.创建其他应用或其他Module的Context 基类Context提供创建其他应用或其他Module的Context的方法为createModuleContext(moduleName:string),创建其他应用或者其他Module的Context,从而通过该Context获取相应的资源信息(例如获取其他Module的…...

数字货币量化交易平台
数字货币量化交易平台是近年来金融科技领域迅速崛起的一种创新型交易方式。它通过应用数学模型和算法策略,实现对数字货币市场的自动交易和风险控制。然而,要在这个竞争激烈的领域中脱颖而出,一个数字货币量化交易平台需要具备足够的专业性&a…...
)
2022 ICPC 济南 E Identical Parity (扩欧)
2022 ICPC 济南 E. Identical Parity (扩欧) Problem - E - Codeforces 大意:给出一个 n 和一个 k , 问是否能构造一个长 n 的排列使得所有长 k 的连续子序列和的奇偶性相同。 思路:通过分析可知 , 任两个间隔 k - 1 的元素奇偶…...

【BUG事务内消息发送】事务内消息发送,事务还未结束,消息发送已被消费,查无数据怎么解决?
问题描述 在一个事务内完成插入操作,通过MQ异步通知其他微服务进行事件处理。 由于是在事务内发送,其他服务消费消息,查询数据时还不存在如何解决呢? 解决方案 通过spring-tx包的TransactionSynchronizationManager事务管理器解…...
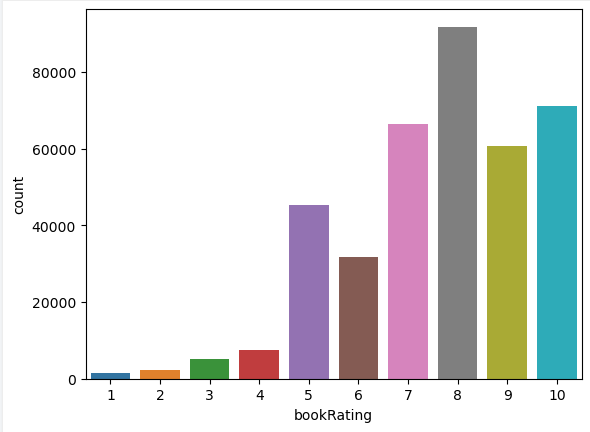
数据分析作业四-基于用户及物品数据进行内容推荐
## 导入支持库 import pandas as pd import matplotlib.pyplot as plt import sklearn.metrics as metrics import numpy as np from sklearn.neighbors import NearestNeighbors from scipy.spatial.distance import correlation from sklearn.metrics.pairwise import pairwi…...

在腾讯云服务器OpenCLoudOS系统中安装svn(有图详解)
1. 安装svn yum -y install subversion 安装成功: 2. 创建数据根目录及仓库 mkdir -p /usr/local/svn/svnrepository 创建test仓库: svnadmin create /usr/local/svn/test test仓库创建成功: 3. 修改配置test仓库 cd /usr/local/svn/te…...

C语言日常刷题5
文章目录 题目答案与解析1234567、 题目 1、以下叙述中正确的是( ) A: 只能在循环体内和switch语句体内使用break语句 B: 当break出现在循环体中的switch语句体内时,其作用是跳出该switch语句体,并中止循环体的执行 C: continue语…...
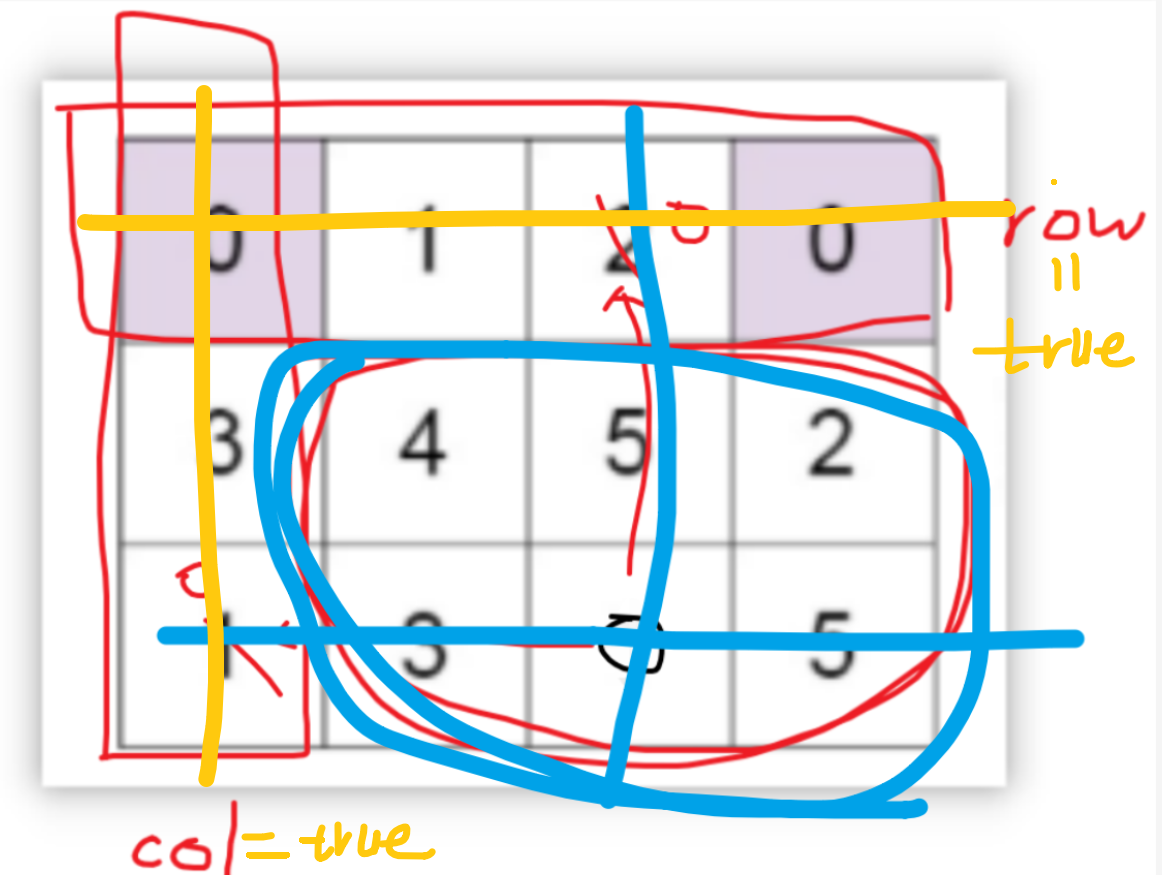
【LeetCode-中等题】73. 矩阵置零
题目 题解一:使用标记数组 public void setZeroes(int[][] matrix) {int m matrix.length;int n matrix[0].length;boolean[] row new boolean[m];boolean[] col new boolean[n];for(int i0; i< m;i){for(int j 0;j<n;j){if (matrix[i][j] 0) row[i]col…...

本地部署 FastGPT
本地部署 FastGPT 1. FastGPT 是什么2. 部署 FastGPT 1. FastGPT 是什么 FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景! …...

软件工程(十八) 行为型设计模式(四)
1、状态模式 简要说明 允许一个对象在其内部改变时改变它的行为 速记关键字 状态变成类 类图如下 状态模式主要用来解决对象在多种状态转换时,需要对外输出不同的行为的问题。比如订单从待付款到待收货的咋黄台发生变化,执行的逻辑是不一样的。 所以我们将状态抽象为一…...
Socket通信与WebSocket协议
文章目录 目录 文章目录 前言 一、Socket通信 1.1 BIO 1.2 NIO 1.3 AIO 二、WebSocket协议 总结 前言 一、Socket通信 Socket是一种用于网络通信的编程接口(API),它提供了一种机制,使不同主机之间可以通过网络进行数据传输和通信…...

新KG视点 | Jeff Pan、陈矫彦等——大语言模型与知识图谱的机遇与挑战
OpenKG 大模型专辑 导读 知识图谱和大型语言模型都是用来表示和处理知识的手段。大模型补足了理解语言的能力,知识图谱则丰富了表示知识的方式,两者的深度结合必将为人工智能提供更为全面、可靠、可控的知识处理方法。在这一背景下,OpenKG组织…...

详解过滤器Filter和拦截器Interceptor的区别和联系
目录 前言 区别 联系 前言 过滤器(Filter)和拦截器(Interceptor)都是用于在Web应用程序中处理请求和响应的组件,但它们在实现方式和功能上有一些区别。 区别 1. 实现方式: - 过滤器是基于Servlet规范的组件,通过实现javax.servlet.Filt…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
