线性代数(五) 线性空间
前言
《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解
空间是什么
大家较熟悉的:平面直角坐标系是最常见的二维空间

空间由无穷多个坐标点组成

每个坐标点就是一个向量

- 反过来,也可说:2维空间,是由无穷多个2维向量构成
- 同样的,在3维空间中,每个3维坐标点就是一个3维向量
- 那么同理:3维空间中有无穷多个3维向量,或3维空间由无穷多个3维向量构成
空间中所有向量,都可被表示成 e 1 ⃗ , e 2 ⃗ , . . . , e n ⃗ \vec{e_{1}},\vec{e_{2}},...,\vec{e_{n}} e1,e2,...,en的线性组合,若有一向量记为: a ⃗ \vec{a} a
a ⃗ = k 1 ⋅ e 1 ⃗ + k 2 ⋅ e 2 ⃗ + . . . + k n ⋅ e n ⃗ , k 1 , k 2 , . . . , k n 有解即可 \vec{a}=k_{1}·\vec{e_{1}}+k_{2}·\vec{e_{2}}+...+k_{n}·\vec{e_{n}} , k_{1},k_{2},...,k_{n}有解即可 a=k1⋅e1+k2⋅e2+...+kn⋅en,k1,k2,...,kn有解即可
则称:这些向量 e 1 ⃗ , e 2 ⃗ , . . . , e n ⃗ \vec{e_{1}},\vec{e_{2}},...,\vec{e_{n}} e1,e2,...,en为这个空间基
线性空间定义及性质



向量相加

[ x 1 y 1 ] + [ x 2 y 2 ] = [ x 1 + x 2 y 1 + y 2 ] = [ 2 + 3 4 + 1 ] \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} + \begin{bmatrix} x_2 \\ y_2 \end{bmatrix} = \begin{bmatrix} x_1 + x_2 \\ y_1+ y_2 \end{bmatrix} = \begin{bmatrix} 2 + 3 \\ 4+ 1 \end{bmatrix} [x1y1]+[x2y2]=[x1+x2y1+y2]=[2+34+1]
数与向量乘法

[ x y ] ∗ 2 = [ 2 x 2 y ] \begin{bmatrix} x \\ y \end{bmatrix} * 2 = \begin{bmatrix} 2x \\ 2y \end{bmatrix} [xy]∗2=[2x2y]
维数,坐标和基

这里出现了一个线性无关的概念,这里线性无关的概念和向量空间中的线性无关差不多,但向量的范围变广了。

- n维线性空间V的基不是唯一的。V中的任意n个线性无关向量都是V的一组基
- 向量 a ⃗ \vec{a} a的坐标 ( a 1 , a 2 , . . . a n ) (a_1,a_2,...a_n) (a1,a2,...an)在 ( ε 1 , ε 2 , . . . ε n ) (\varepsilon_1,\varepsilon_2,...\varepsilon_n) (ε1,ε2,...εn)基下,是唯一且确定的
要怎么确定线性空间的维数与基

欧几里得空间
欧几里得空间是空间中的一种类型,是一种特殊的集合。欧几里得集合中的元素:有序实数元组
例:(2,3)(2,4)(3,4)(3,5)为有序实数2元组
- 有序是指:如(2,3)和(3,2)是两个不同的元素
- 也就是:每个元素内的实数是讲顺序的
- 实数是指:每个元素内的数字都∈R
- 元组是指:每个元素有有序几个数字构成
- 如:2个数字构成=2元组,n个数字构成=n元组
欧几里得集合=有序实数元组=n维坐标点的集合
所以,欧几里得空间就是我们从小到大进场使用的那个空间
欧几里得空间符合空间的8大定理
子空间
子空间,是整个空间的一部分。但它也是空间,必须满足向量空间的定义。

子空间的交集

子空间的和
子空间的 V 1 , V 2 V_1,V_2 V1,V2的并集,并不是简单的元素相加,造成“子空间的并集不属于子空间”。

所以定义子空间的和

子空间的直和

子空间直和是特殊的和。基要求各子空间互相独立。
可以把整个线性空间看成一个大蛋糕。
- 直和分解就是把蛋糕切成小块的,每一小块蛋糕都是一个子空间,所有小蛋糕之间没有交集,且它们能拼成整个蛋糕。
- 子空间的和就是分蛋糕的时候没切好,小蛋糕拼不成整个蛋糕(子空间之间的交集非空).
内积空间
在之前的内容中,我们抽象的介绍了向量,矩阵以及线性空间线性变换等。但是在几何中,向量还有向量的模,向量的内积运算等。为了引入向量的模,向量的内积等运算,我们引入了“内积定义”。即内积空间=线性空间+内积定义。


向量的夹角

cos θ = cos ( α − β ) = cos ( α ) cos ( β ) + sin ( α ) sin ( β ) = x 1 x 1 2 + y 1 2 ∗ x 2 x 2 2 + y 2 2 + y 1 x 1 2 + y 1 2 ∗ y 2 x 2 2 + y 2 2 \cos\theta = \cos(\alpha-\beta) =\cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta)=\cfrac{x_1}{\sqrt{\gdef\bar#1{#1^2} \bar{x_1} + \bar{y_1} }} * \cfrac{x_2}{\sqrt{\gdef\bar#1{#1^2} \bar{x_2} + \bar{y_2} }} + \cfrac{y_1}{\sqrt{\gdef\bar#1{#1^2} \bar{x_1} + \bar{y_1} }} * \cfrac{y_2}{\sqrt{\gdef\bar#1{#1^2} \bar{x_2} + \bar{y_2} }} cosθ=cos(α−β)=cos(α)cos(β)+sin(α)sin(β)=x12+y12x1∗x22+y22x2+x12+y12y1∗x22+y22y2
cos θ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 = a ⃗ ∗ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ \cos\theta = \cfrac{x_1x_2+y_1y_2}{\sqrt{\gdef\bar#1{#1^2} \bar{x_1} + \bar{y_1}}\sqrt{\gdef\bar#1{#1^2} \bar{x_2} + \bar{y_2}}} = \cfrac{\vec{a} *\vec{b}}{|\vec{a} ||\vec{b}|} cosθ=x12+y12x22+y22x1x2+y1y2=∣a∣∣b∣a∗b
上述的a,b向量,只是在2维坐标系中,如果将坐标系转为n维度,即向量a为(x1,x2,x3…xn)向量b为(y1,y2,y3…yn)
cos θ = ∑ i = 1 n ( x i ∗ y i ) ∑ i = 1 n x i 2 ∑ i = 1 n y i 2 = [ a , b ] [ a , a ] [ b , b ] \cos\theta = \cfrac{\sum_{i=1}^n(x_i*y_i)}{\sqrt{\sum_{i=1}^n\gdef\bar#1{#1^2} \bar{x_i}}\sqrt{\sum_{i=1}^n\gdef\bar#1{#1^2} \bar{y_i}}}=\cfrac{[a,b]}{\sqrt{[a,a]}\sqrt{[b,b]}} cosθ=∑i=1nxi2∑i=1nyi2∑i=1n(xi∗yi)=[a,a][b,b][a,b]
两个向量的夹角 θ \theta θ=90°,即两个向量正交.
两个向量相互正交,把这2个向量合为一组向量,就叫正交向量组

正交基

如果 ∣ e n ∣ = 1 |e_n|=1 ∣en∣=1,则称为标准正交基
施密特(Schmidt)求解正交基
通过简单的投影方式,可以找到一基的正交基

已知一组基{KaTeX parse error: Expected 'EOF', got '}' at position 18: …lpha_1,\alpha_2}̲求其正交基组
- 令 β 1 = α 1 \beta_1=\alpha_1 β1=α1
- 得 β 1 \beta_1 β1的上的单位基为 β 1 [ β 1 , β 1 ] \cfrac{\beta_1}{\sqrt{[\beta_1,\beta_1]}} [β1,β1]β1
- 计算 α 1 \alpha_1 α1在 β 1 \beta_1 β1上的投影
- 计算投影长度, [ α 2 , β 1 ] [ α 2 , α 2 ] [ β 1 , β 1 ] ∗ [ α 2 , α 2 ] \cfrac{[\alpha_2,\beta_1]}{\sqrt{[\alpha_2,\alpha_2]}\sqrt{[\beta_1,\beta_1]}} *\sqrt{[\alpha_2,\alpha_2]} [α2,α2][β1,β1][α2,β1]∗[α2,α2]
- 投影为长度* β 1 \beta_1 β1的上的单位基 [ α 2 , β 1 ] [ β 1 , β 1 ] ∗ β 1 \cfrac{[\alpha_2,\beta_1]}{[\beta_1,\beta_1]} *\beta_1 [β1,β1][α2,β1]∗β1
- 得正交基为 α 2 − [ α 2 , β 1 ] [ β 1 , β 1 ] ∗ β 1 \alpha_2 - \cfrac{[\alpha_2,\beta_1]}{[\beta_1,\beta_1]} *\beta_1 α2−[β1,β1][α2,β1]∗β1
- 正交基组为{ α 2 − [ α 2 , β 1 ] [ β 1 , β 1 ] ∗ β 1 , [ α 2 , β 1 ] [ β 1 , β 1 ] ∗ β 1 \alpha_2 - \cfrac{[\alpha_2,\beta_1]}{[\beta_1,\beta_1]} *\beta_1,\cfrac{[\alpha_2,\beta_1]}{[\beta_1,\beta_1]} *\beta_1 α2−[β1,β1][α2,β1]∗β1,[β1,β1][α2,β1]∗β1}
如果是三维的话

正交补
定义: 设 U U U是 V V V的子空间,则 U ⊥ = { v ∈ V : ∀ u ∈ U < v , u > = 0 } U^\perp =\{v\in V : \forall u\in U \left< v,u\right> =0 \} U⊥={v∈V:∀u∈U⟨v,u⟩=0}称之为 U U U的正交补. ∀ u \forall u ∀u表示集合中所有u的意思
- U ⊥ U^\perp U⊥是 V V V的子空间;
- V ⊥ = { 0 } V^\perp=\{0\} V⊥={0}且 { 0 } ⊥ = V \{0\}^\perp=V {0}⊥=V
- U ⊥ ∩ U = { 0 } U^\perp \cap U = \{0\} U⊥∩U={0};
- 如果 U , W U,W U,W都是 V V V的子集,且 U ⊆ W U\sube W U⊆W ,则 W ⊥ ⊆ U ⊥ W^\perp \sube U^\perp W⊥⊆U⊥
定理: 有限维子空间的正交分解: V = U ⊕ U ⊥ V= U \oplus U^\perp V=U⊕U⊥
- ( U ⊥ ) ⊥ = U (U^\perp)^\perp=U (U⊥)⊥=U
- dim V = dim U + dim U ⊥ \dim V = \dim U + \dim U^\perp dimV=dimU+dimU⊥
如何求解正交补的基?
- 假设 d i m V = 3 , d i m U = 2 且基组为 [ { 1 , 0 , 0 } , { 0 , 1 , 0 } ] dim V = 3 , dim U = 2 且基组为[\{1,0,0\},\{0,1,0\}] dimV=3,dimU=2且基组为[{1,0,0},{0,1,0}]
- 得矩阵 A = [ 1 0 0 0 1 0 0 0 0 ] A=\begin{bmatrix} 1 &0&0 \\ 0&1&0 \\ 0&0&0 \end{bmatrix} A= 100010000
- 假设 U ⊥ U^\perp U⊥的基组 x ⃗ = [ x y z ] \vec{x}=\begin{bmatrix} x\\ y\\ z \end{bmatrix} x= xyz
- 得 A x = 0 Ax=0 Ax=0齐次方程组,你通解为{0,0,1}
正交补的基就是方程组的解,解数=dim V - R(A)
主要参考
《欧几里得空间是向量空间》
《生成空间是什么》
《子空间的交与和》
《3.10子空间的运算》
《正交基与标准正交基》
《如何理解施密特(Schmidt)正交化》
《正交补 (orthogonal complements)》
相关文章:

线性代数(五) 线性空间
前言 《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解 空间是什么 大家较熟悉的:平面直角坐标系是最常见的二维空间 空间由无穷多个坐标点组成 每个坐标点就是一个向量 反过来,也可说&…...
kafka--技术文档--spring-boot集成基础简单使用
阿丹: 查阅了很多资料了解到,使用了spring-boot中整合的kafka的使用是被封装好的。也就是说这些使用其实和在linux中的使用kafka代码的使用其实没有太大关系。但是逻辑是一样的。这点要注意! 使用spring-boot整合kafka 1、导入依赖 核心配…...
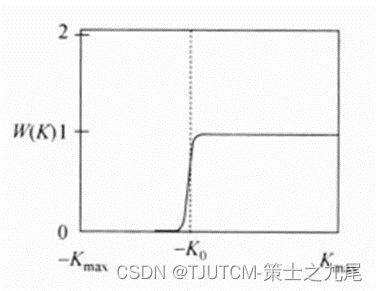
【核磁共振成像】部分傅里叶重建
目录 一、部分傅里叶重建二、部分傅里叶重建算法2.1 填零2.2 零差处理 一、部分傅里叶重建 在部分傅里叶采集中,数据并不是绕K空间中心对称收集的,而是K空间的一半是完全填充的,另一半只收集了一小部分数据。 部分傅里叶采集所依据的原理…...

React中的flushSync与Vue中的nextTick的比较
React中的flushSync与Vue中的nextTick是两种用于处理异步更新的机制。它们在React和Vue这两个流行的前端框架中起着重要的作用。 首先,让我们来看看flushSync。在React中,当需要更新UI时,React会将更新操作放入一个队列中,然后异…...

golang设置国内镜像源
以windows为例, 在cmd 窗口中执行下列语句 go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.io,direct 或者 1.运行 go env -w GO111MODULEon //开启mod 运行 go env -w GOPROXYhttps://goproxy.cn,direct //设置代理 执…...

linux切换到root没有conda环境
这个错是因为 没有将anaconda添加到环境变量 export PATH"/home/tao/anaconda3/bin:$PATH"然后 source ~/.bashrc或者写入 nano ~/.bashrc在文件的末尾添加以下行 export PATH"/home/tao/anaconda3/bin:$PATH"再 source ~/.bashrc就可以了...

数据库——redis介绍
文章目录 redis是什么?分布式缓存常见的技术选型方案有哪些?说一下 Redis 和 Memcached 的区别和共同点? redis是什么? 简单来说 Redis 就是一个使用 C 语言开发的数据库,不过与传统数据库不同的是 Redis 的数据是存在…...
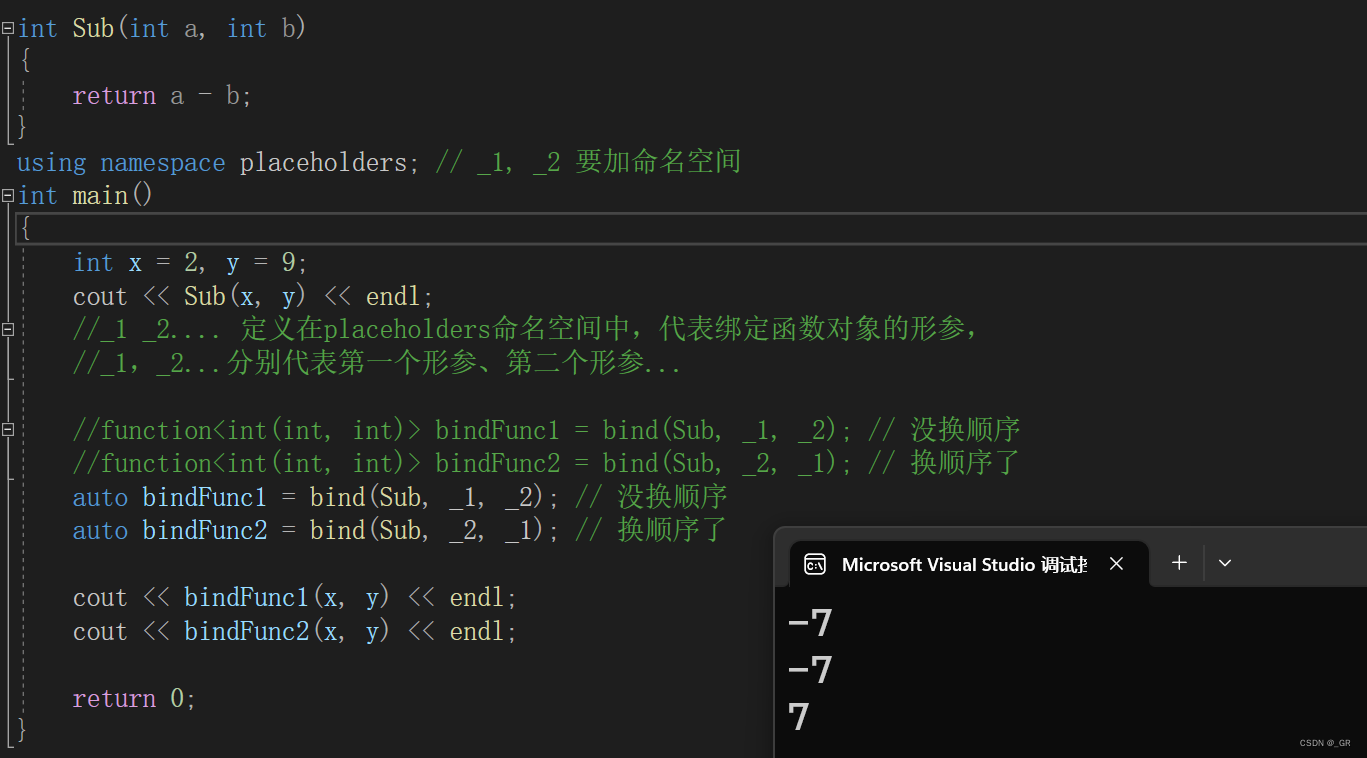
从C语言到C++_34(C++11_下)可变参数+ lambda+function+bind+笔试题
目录 1. 可变参数模板 1.1 展开参数包 1.1.1 递归函数方式展开 1.1.2 逗号表达式展开 1.2 emplace相关接口 2. lambda表达式(匿名函数) 2.1 C11之前函数的缺陷 2.2 lambda表达式语法 2.3 函数对象与lambda表达式 3. 包装器 3.1 function包装器…...

喜报|星瑞格荣获“2022-2023年度国产数据库应用优秀解决方案”奖项
近日,赛迪网为表彰数字赛道上的先行者,联合《数字经济》杂志社和北京科创互联,共同组织以“树立行业标杆,引领服务创新”为中心的“2022-2023年度产业数字服务案例及创新成果征集活动”。该活动旨在鼓励各行业数字化应用技术创新树…...

【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式
【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式 文章目录 【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式一、概述二、什么是幂等性三、幂等性需关注几个重点四、幂等性有什么用五、常见用来保证幂等的手段5.1 MVCC方案5.2 去重表5.3 去重表5.4 select in…...
2023.8.26-2023.9.3 周报【3D+GAN+Diffusion基础知识+训练测试】
目录 学习目标 学习内容 学习时间 学习产出 学习目标 1. 3D方向的基础知识 2. 图像生成的基础知识(GAN \ Diffusion) 3. 训练测试GAN和Diffusion 学习内容 1. 斯坦福cv课程-3D (网课含PPT) 2. sjtu生成模型课件 3. ge…...

如何使用CSS创建渐变阴影?
随着网络的不断发展,制作漂亮的 UI 是提高客户在网站上的参与度的最重要的工作之一。改善前端外观的方法之一是在 CSS 中应用渐变阴影。应用渐变阴影的两种最重要的方法是线性渐变和径向渐变。 渐变阴影可用于吸引用户对特定信息的注意力,应用悬停或焦点…...

perl send HTTP Request
perl send HTTP Request 使用Perl进行发送HttP请求 use LWP::UserAgent; use HTTP::Request; use HTTP::Headers; use JSON::PP;my $test_url "htttp://127.0.0.1:8080/update/";sub sendHttp{my $user_agent LWP::UserAgent->new(timeout>60);my ($url, $…...
阿里云CDN缓存预热与刷新以及常见的故障汇总
文章目录 1.为CDN缓存的文件增加过期时间2.CDN缓存预热配置3.CDN缓存刷新配置4.常见故障 CDN缓存预热指的是主动将要缓存的文件推送到全国各地的CDN边缘加速器上,减少回源率,提供命中率。 缓存刷新指的是后期上传了同名的文件,之前的缓存已经…...
Oracle创建控制列表ACL(Access Control List)
Oracle创建控制列表ACL(Access Control List) Oracle ACL简介一、先登陆163邮箱设置开启SMTP。二、Oracle ACL控制列表处理(一)创建ACL(create_acl)(二)添加ACL权限(add_…...

3D模型转换工具HOOPS Exchange助力打造虚拟现实应用程序
挑战: 支持使用各种 CAD 系统和 CAD 文件格式的客户群向可视化硬件提供快速、准确的数据加载提供对详细模型信息的访问,同时确保高帧率性能 解决方案: HOOPS Exchange领先的CAD数据转换工具包 结果: 确保支持来自领先工程软件…...
python web GUI框架-NiceGUI 教程(二)
python web GUI框架-NiceGUI 教程(二) streamlit可以在一些简单的场景下仍然推荐使用,但是streamlit实在不灵活,受限于它的核心机制,NiceGUI是一个灵活的web框架,可以做web网站也可以打包成独立的exe。 基…...

RT_Thread内核机制学习(二)
对于RTT来说,每个线程创建时都自带一个定时器 rt_err_t rt_thread_sleep(rt_tick_t tick) {register rt_base_t temp;struct rt_thread *thread;/* set to current thread */thread rt_thread_self();RT_ASSERT(thread ! RT_NULL);RT_ASSERT(rt_object_get_type(…...
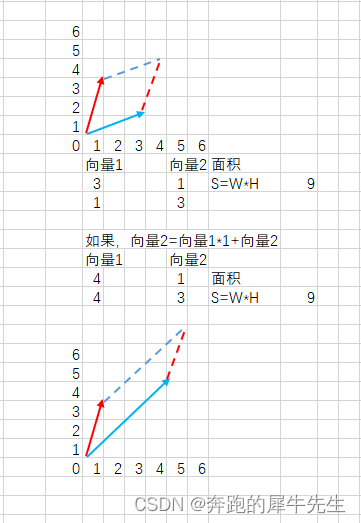
线性代数的学习和整理12: 矩阵与行列式,计算上的差别对比
目录 1 行列式和矩阵的比较 2 简单总结矩阵与行列式的不同 3 加减乘除的不同 3.1 加法不同 3.2 减法不同 3.3 标量乘法/数乘 3.3.1 标准的数乘对比 3.3.2 数乘的扩展 3.4 乘法 4 初等线性变换的不同 4.1 对矩阵进行线性变换 4.2 对行列式进行线性变换 1 行列式和…...

2023年MySQL核心技术面试第一篇
目录 一 . 存储:一个完整的数据存储过程是怎样的? 1.1 数据存储过程 1.1.1 创建MySQl 数据库 1.1.1.1 为什么我们要先创建一个数据库,而不是直接创建数据表? 1.1.1.2基本操作部分 1.2 选择索引问题 二 . 字段:这么多的…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
