线性代数的学习和整理12: 矩阵与行列式,计算上的差别对比
目录
1 行列式和矩阵的比较
2 简单总结矩阵与行列式的不同
3 加减乘除的不同
3.1 加法不同
3.2 减法不同
3.3 标量乘法/数乘
3.3.1 标准的数乘对比
3.3.2 数乘的扩展
3.4 乘法
4 初等线性变换的不同
4.1 对矩阵进行线性变换
4.2 对行列式进行线性变换
1 行列式和矩阵的比较
- 如果矩阵行数列数相等,那么这个矩阵是方阵,只有方阵才有行列式
- 行列式必须是行列数相等。行列式是方阵的一种特殊运算,加减乘除规则都和矩阵不同
2 简单总结矩阵与行列式的不同
- 区别1
- 矩阵是一个n*m的数表 矩阵是多个向量 ; 矩阵的行数和列数可以不同;
- 行列式是一个n阶的方阵样式的;
- 区别2
- 矩阵不能从整体上被看成一个数, 矩阵是多个向量 ;
- 行列式最终可以算出来变成一个数/标量;
- 区别3
- 加法不同
- 减法不同
- 数乘不同
- 乘法完全不同,不可比
- 区别4
- 线性变化的交换,行列式不同
- 线性变化的倍数,行列式不同
- 线性变化的倍加,行列式不变,是相同的
3 加减乘除的不同
3.1 加法不同
- 矩阵加法,两个矩阵都是n*m,A+B = 对应元素相加
- 行列式加法,见下图,只是某1行/列相加
3.2 减法不同
- 减法的差别,参考加法
3.3 标量乘法/数乘
3.3.1 标准的数乘对比
- 矩阵的标量乘法 λ*A=λ*每个元素,*A*B=A*λ*B
- 行列式的标量乘法,λ*|A|=λ*某1行/列
3.3.2 数乘的扩展
矩阵的数乘
- 矩阵的标量乘法始终如此 (λ*A)=λ*(A)
行列式得数乘扩展
- 行列式的标量乘法,|λ*A|=λ^n*|A| ,其中n是满秩矩阵A的秩/维度
- 行列数乘法: |Ann*Bnn| =|Ann|*|Bnn|
- 行列数乘法: |2Ann*Bnn| =|2Ann|*|Bnn| =2^n*|Ann|*|Bnn|
- 里面是矩阵的数乘,矩阵(假设是方阵)的数乘是每行每列都*λ
- 而行列式的数乘是 某1行/列*λ
- 因此每行的λ 都可以提出来,因此是n 个λ 相乘=λ^n
3.4 乘法
- 矩阵乘法
- 矩阵乘法:点乘
- 矩阵乘法:叉乘
- 行列式应该只有标量乘法,没有其他乘法吧?
4 初等线性变换的不同
线性变换包含,行的线性变换和列的线性变换
行的线性变换
- 行之间,交换
- 某行乘以倍数
- 某行乘倍数+到其他行
列的线性变换
- 列之间,交换
- 某列乘以倍数
- 某列乘倍数+到其他列
4.1 对矩阵进行线性变换
- 无论是线性行变换,还是线性列变换,矩阵还是等价得
- 交换某行/列
- 倍数
- 倍加
-
矩阵进行线性变换后的结果
- 线性变换前后系统的特征值不变;
- 线性变换前后系统的传递函数矩阵不变;
4.2 对行列式进行线性变换
- 交换:如果交换行列式|A| 的任意两行/列,增加一个负号-
- 倍数:如果行列式|A| 某1行或列*λ,|A| 变成 λ*|A|
- 倍加:如果行列式|A| 某1行或列*λ后,再加到另外某1行/列,|A| 不变还是=|A|
- 总结,只有进行倍加的线性变换之后,行列式才不变化
解释原因
- 因为行列式其实代表有向的面积比,所以交换行列式|A| 的任意两行/列,增加一个负号-
- 因为行列式的标量乘法 λ*|A|= 把行列式的某1行/列* λ,所以行列式|A| 某1行或列*λ,|A| 变成 λ*|A|
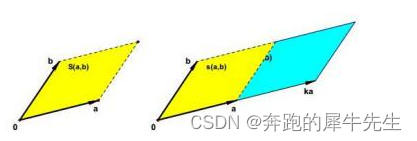
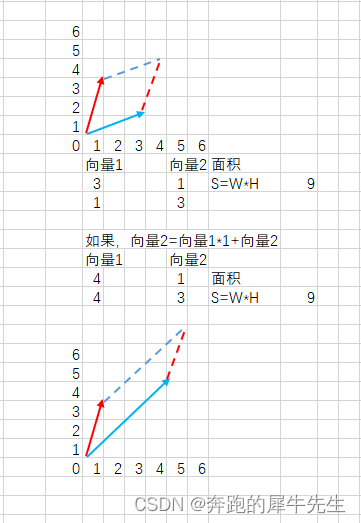
- 因为行列式其实代表有向的面积比,所以行列式|A| 某1行或列*λ后,再加到另外某1行/列,|A| 不变还是=|A|
相关文章:

线性代数的学习和整理12: 矩阵与行列式,计算上的差别对比
目录 1 行列式和矩阵的比较 2 简单总结矩阵与行列式的不同 3 加减乘除的不同 3.1 加法不同 3.2 减法不同 3.3 标量乘法/数乘 3.3.1 标准的数乘对比 3.3.2 数乘的扩展 3.4 乘法 4 初等线性变换的不同 4.1 对矩阵进行线性变换 4.2 对行列式进行线性变换 1 行列式和…...

2023年MySQL核心技术面试第一篇
目录 一 . 存储:一个完整的数据存储过程是怎样的? 1.1 数据存储过程 1.1.1 创建MySQl 数据库 1.1.1.1 为什么我们要先创建一个数据库,而不是直接创建数据表? 1.1.1.2基本操作部分 1.2 选择索引问题 二 . 字段:这么多的…...

linux启动jar 缺失lib
linux启动jar包时,找不到报错 [rootebs-141185 xl-admin]# java -Djava.library.path/home/kabangke/xl-admin/lib -jar /home/kabangke/xl-admin/xl-admin.jar Exception in thread "main" java.lang.NoClassDefFoundError: org/springframework/web/se…...

【Bash】常用命令总结
文章目录 1. 文件查询1.1 查看文件夹内(包含子文件夹)文件数量1.2 查看文件夹大小 任务简介: 对bash常用命令进行总结。 任务说明: 对平时工作中使用bash的相关命令做一个记录和说明,方便以后查阅。 1. 文件查询 1.…...
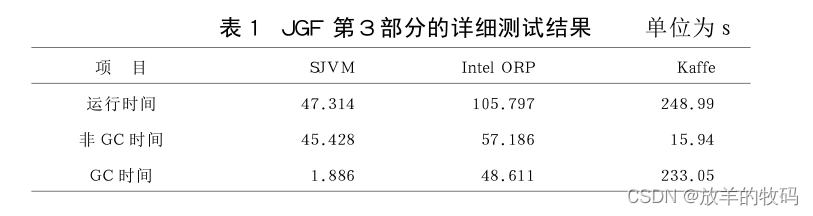
小研究 - Java虚拟机性能及关键技术分析
利用specJVM98和Java Grande Forum Benchmark suite Benchmark集合对SJVM、IntelORP,Kaffe3种Java虚拟机进行系统测试。在对测试结果进行系统分析的基础上,比较了不同JVM实现对性能的影响和JVM中关键模块对JVM性能的影响,并提出了提高JVM性能的一些展望。…...

Repo manifests默认default.xml清单文件中的各个标签详解
Repo简介 “Repo” 是一个用于管理多个Git存储库的工具,通常与Google的Android开发项目一起使用。它允许您在一个命令下轻松地进行多个Git存储库的同步、下载和管理。 repo下载安装 从清华镜像源下载 mkdir ~/bin PATH~/bin:$PATH curl https://mirrors.tun…...
javacv基础02-调用本机摄像头并预览摄像头图像画面视频
引入架包: <dependency><groupId>org.openpnp</groupId><artifactId>opencv</artifactId><version>4.5.5-1</version></dependency><dependency><groupId>org.bytedeco</groupId><artifactId…...
缓冲区与响应头)
【Nginx21】Nginx学习:FastCGI模块(三)缓冲区与响应头
Nginx学习:FastCGI模块(三)缓冲区与响应头 缓存相关的内容占了 FastCGI 模块将近一小半的内容,当然,用过的人可能不多。而今天的内容说实话,我平常也没怎么用过。第一个是缓冲区相关的知识,其实…...
)
正则表达式(常用字符简单版)
量词 字符类 边界匹配 分组和捕获 特殊字符 字符匹配 普通字符:普通字符按照字面意义进行匹配,例如匹配字母 "a" 将匹配到文本中的 "a" 字符。元字符:元字符具有特殊的含义,例如 \d 匹配任意数字字符…...

从零开始学习Python爬虫:详细指南
导言: 随着互联网的迅速发展,大量的数据可供我们利用。而Python作为一种简单易学且功能强大的编程语言,被广泛应用于数据分析和处理。学习Python爬虫技术,能够帮助我们从互联网上获取数据,并进行有效地分析和利用。本文…...
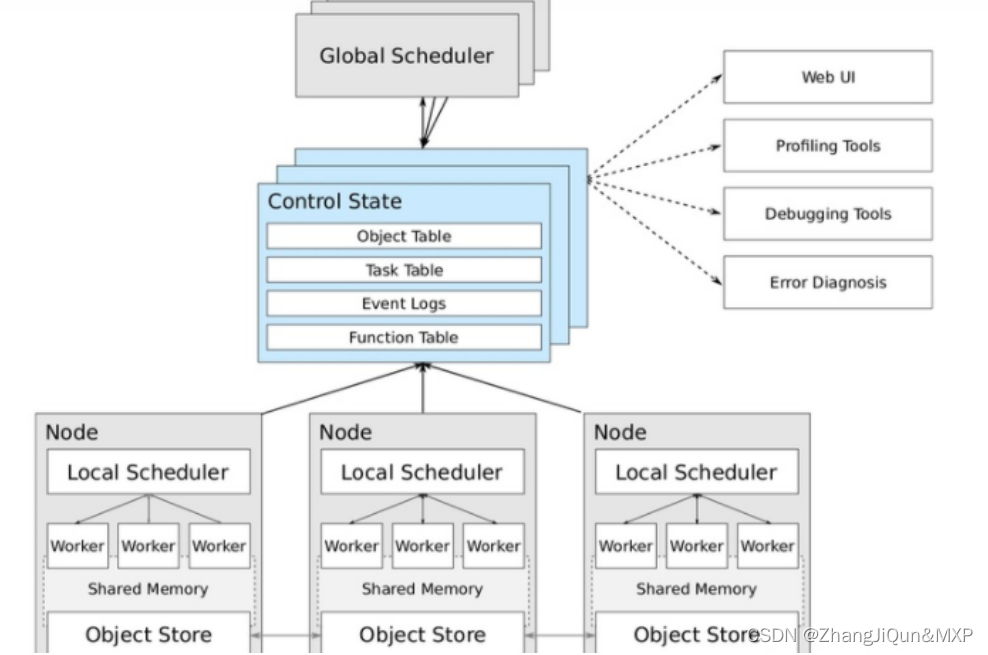
分布式计算框架:Spark、Dask、Ray
目录 什么是分布式计算 分布式计算哪家强:Spark、Dask、Ray 2 选择正确的框架 2.1 Spark 2.2 Dask 2.3 Ray 什么是分布式计算 分布式计算是一种计算方法,和集中式计算是相对的。 随着计算技术的发展,有些应用需要非常巨大的计算能力才…...

什么是伪类链(Pseudo-class Chaining)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ Pseudo-class Chaining⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为那些对Web开发感兴趣、刚刚…...

每日一题:leetcode 57 插入区间
给你一个 无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 示例 1: 输入:intervals [[1,3…...

第五节:实现自己的第一个environment
本专栏是强化学习运用在买卖股票之上的入门学习内容。 主要解决强化学习代码落地和代码实践,不需要学习相关数学原理,直观简单的带领读者入门强化学习炒股。 查看本专栏完整内容,请访问:https://blog.csdn.net/windanchaos/category_12391143.html 本文发布地址:https://b…...

无套路,财务数据分析-多组织损益表分析分享
在报表众多的财务数据分析中,损益表是老板们最关注的报表,特别是当有多组织时,损益表的分析就变得更加重要了。以前受限于数据分析工具,做损益表分析时很难做到多维度灵活分析,但随着BI数据可视化工具的发展࿰…...

Java并发编程第6讲——线程池(万字详解)
Java中的线程池是运用场景最多的并发框架,几乎所有需要异步或并发执行任务的程序都可以使用线程池,本篇文章就详细介绍一下。 一、什么是线程池 定义:线程池是一种用于管理和重用线程的技术(池化技术),它主…...

AI + Milvus:将时尚应用搭建进行到底
在上一篇文章中,我们学习了如何利用人工智能技术(例如开源 AI 向量数据库 Milvus 和 Hugging Face 模型)寻找与自己穿搭风格相似的明星。在这篇文章中,我们将进一步介绍如何通过对上篇文章中的项目代码稍作修改,获得更…...
归并排序(Java 实例代码)
目录 归并排序 一、概念及其介绍 二、适用说明 三、过程图示 四、Java 实例代码 MergeSort.java 文件代码: 归并排序 一、概念及其介绍 归并排序(Merge sort)是建立在归并操作上的一种有效、稳定的排序算法,该算法是采用分…...

【VUE】数字动态变化到目标值-vue-count-to
vue-count-to是一个Vue组件,用于实现数字动画效果。它可以用于显示从一个数字到另一个数字的过渡动画。 插件名:vue-count-to 官方仓库地址:GitHub - PanJiaChen/vue-countTo: Its a vue component that will count to a target number at a…...
)
Mysql /etc/my.cnf参数详解(二)
#buffer相关 #buffer pool根据实际内存大小调整,标准为物理内存的50% innodb_buffer_pool_size15996M //默认值128M,innodb_buffer_pool_size | 134217728 key_buffer_size 33554432 #根据物理内存大小设置 确保每个instance内的内存2G左右 <5000 1,>5000 &…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
