macOS 安装 Homebrew 详细过程
文章目录
- macOS 安装 Homebrew 详细过程
- Homebrew 简介
- Homebrew 安装过程
- 设置环境变量
- 安装 Homebrew
- 安装完成
- 后续设置(重要)
- 设置环境变量
- homebrew 镜像源设置

macOS 安装 Homebrew 详细过程
本文讲解了如何使用中科大源安装 Homebrew 的安装过程,文章里面的所有步骤都是必要的,需要的同学直接复制粘贴到您的Terminal(终端程序) 中运行即可.
Homebrew 简介
Homebrew 是一个开源的包管理器,专为 macOS 设计,但后来也被扩展到了 Linux。它允许用户轻松地安装、更新和管理软件包。以下是关于 Homebrew 的一些关键点:
-
简单性:Homebrew 提供了一个简单的命令行界面,使得安装和管理软件变得非常容易。例如,要安装一个软件包,只需输入
brew install <软件名>。 -
公式 (Formulae):在 Homebrew 中,软件包被称为“公式”。公式是一些 Ruby 脚本,描述了如何安装软件及其依赖关系。
-
Cask:除了命令行工具和库,Homebrew 还有一个叫做 “Homebrew Cask” 的扩展,允许用户从命令行安装 macOS 的图形界面应用程序。
-
Bottles:Bottles 是 Homebr
相关文章:

macOS 安装 Homebrew 详细过程
文章目录 macOS 安装 Homebrew 详细过程Homebrew 简介Homebrew 安装过程设置环境变量安装 Homebrew安装完成后续设置(重要)设置环境变量homebrew 镜像源设置macOS 安装 Homebrew 详细过程 本文讲解了如何使用中科大源安装 Homebrew 的安装过程,文章里面的所有步骤都是必要的,需…...
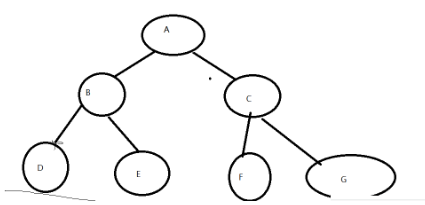
数据结构之树型结构
相关概念树的表示二叉树二叉树性质二叉树储存 实现一颗二叉树创建遍历(前中后序)获取树中节点个数获取叶子节点个数获取第k层节点个数获取二叉树高度检测值为value元素是否存在层序遍历(需要队列来实现)判断是否为完全二叉树&…...
指针进阶详解
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.字符指针 2.指针数组 3.数组指针 4.数组传…...
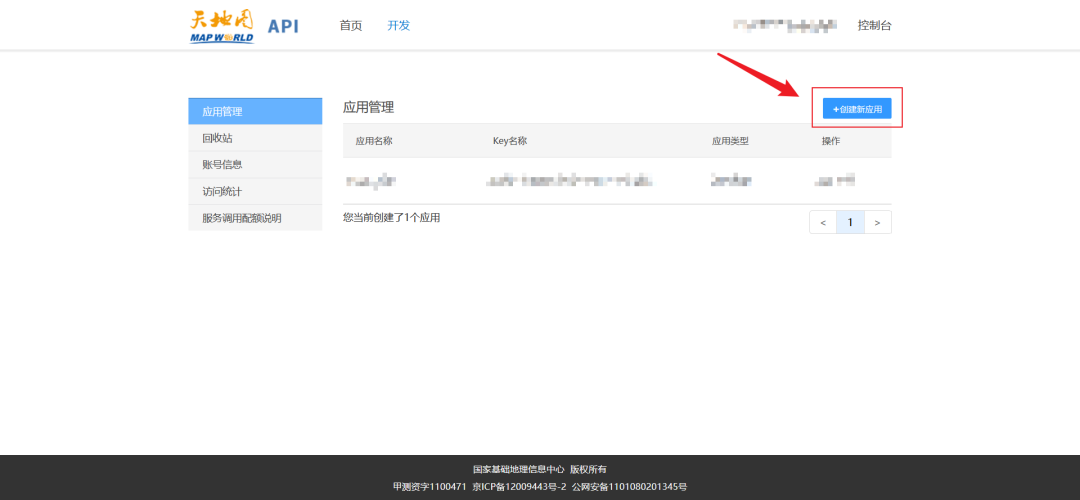
QGIS 如何添加天地图
相信很多小伙伴在 QGIS 里面添加天地图的时候一定感觉很困惑,按照官网的操作申请 Key 之后,添加相对应的服务地址之后看不到地图或者地图不正常显示,今天我们就来解决这个问题 以下所有操作基于 QGIS 3.22 版本 申请 Key 1. 添加天地图的第一步需要申请 Key,首先要注册天…...

PHP8内置函数中的数学函数-PHP8知识详解
php8中提供了大量的内置函数,以便程序员直接使用常见的内置函数包括数学函数、变量函数、字符串函数、时间和日期函数等。今天介绍内置函数中的数学函数。 本文讲到了数学函数中的随机数函数rand()、舍去法取整函数floor()、向上取整函数 ceil()、对浮点数进行四舍…...
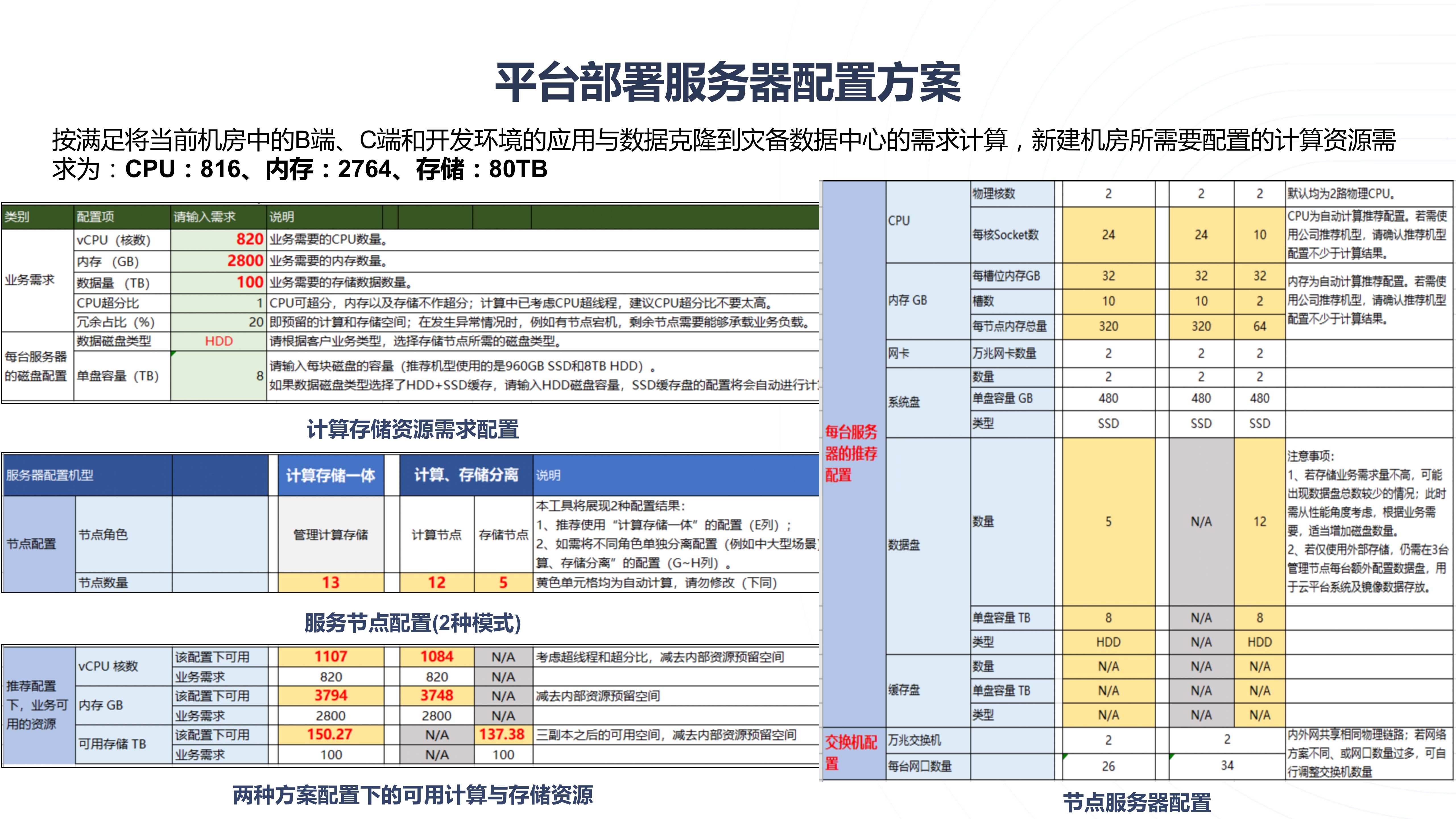
云计算企业私有云平台建设方案PPT
导读:原文《云计算企业私有云平台建设方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 喜欢文章,您可以点赞评论转发本文,…...

ORA-01174: DB_FILES be compatible RAC rolling fashion complete outage
How to change the DB_FILES parameter in RAC (Doc ID 1636681.1)编辑To Bottom In this Document Goal Solution APPLIES TO: Oracle Database - Enterprise Edition - Version 10.1.0.2 and later Oracle Database Cloud Schema Service - Version N/A and later Oracle…...

线性代数(五) 线性空间
前言 《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解 空间是什么 大家较熟悉的:平面直角坐标系是最常见的二维空间 空间由无穷多个坐标点组成 每个坐标点就是一个向量 反过来,也可说&…...
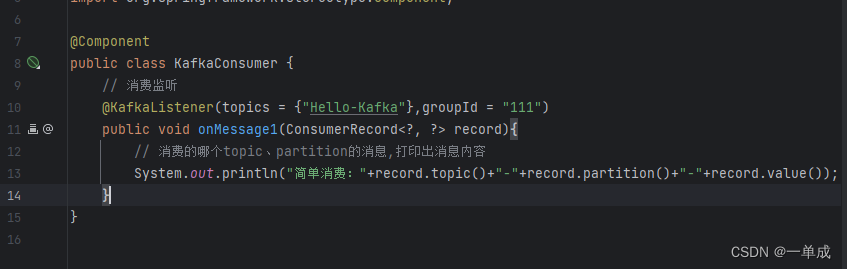
kafka--技术文档--spring-boot集成基础简单使用
阿丹: 查阅了很多资料了解到,使用了spring-boot中整合的kafka的使用是被封装好的。也就是说这些使用其实和在linux中的使用kafka代码的使用其实没有太大关系。但是逻辑是一样的。这点要注意! 使用spring-boot整合kafka 1、导入依赖 核心配…...
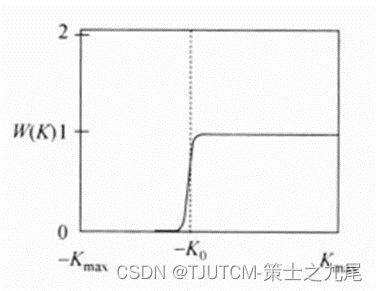
【核磁共振成像】部分傅里叶重建
目录 一、部分傅里叶重建二、部分傅里叶重建算法2.1 填零2.2 零差处理 一、部分傅里叶重建 在部分傅里叶采集中,数据并不是绕K空间中心对称收集的,而是K空间的一半是完全填充的,另一半只收集了一小部分数据。 部分傅里叶采集所依据的原理…...

React中的flushSync与Vue中的nextTick的比较
React中的flushSync与Vue中的nextTick是两种用于处理异步更新的机制。它们在React和Vue这两个流行的前端框架中起着重要的作用。 首先,让我们来看看flushSync。在React中,当需要更新UI时,React会将更新操作放入一个队列中,然后异…...

golang设置国内镜像源
以windows为例, 在cmd 窗口中执行下列语句 go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.io,direct 或者 1.运行 go env -w GO111MODULEon //开启mod 运行 go env -w GOPROXYhttps://goproxy.cn,direct //设置代理 执…...

linux切换到root没有conda环境
这个错是因为 没有将anaconda添加到环境变量 export PATH"/home/tao/anaconda3/bin:$PATH"然后 source ~/.bashrc或者写入 nano ~/.bashrc在文件的末尾添加以下行 export PATH"/home/tao/anaconda3/bin:$PATH"再 source ~/.bashrc就可以了...

数据库——redis介绍
文章目录 redis是什么?分布式缓存常见的技术选型方案有哪些?说一下 Redis 和 Memcached 的区别和共同点? redis是什么? 简单来说 Redis 就是一个使用 C 语言开发的数据库,不过与传统数据库不同的是 Redis 的数据是存在…...
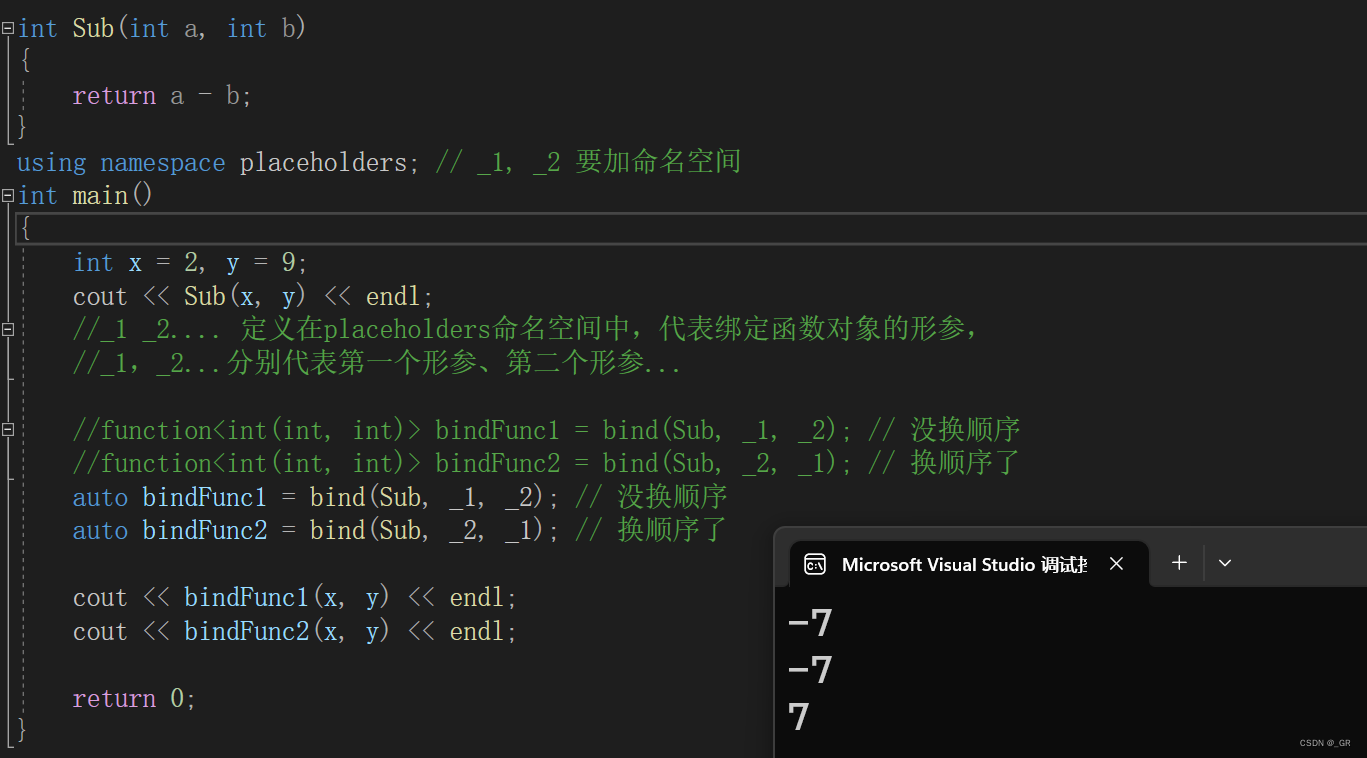
从C语言到C++_34(C++11_下)可变参数+ lambda+function+bind+笔试题
目录 1. 可变参数模板 1.1 展开参数包 1.1.1 递归函数方式展开 1.1.2 逗号表达式展开 1.2 emplace相关接口 2. lambda表达式(匿名函数) 2.1 C11之前函数的缺陷 2.2 lambda表达式语法 2.3 函数对象与lambda表达式 3. 包装器 3.1 function包装器…...

喜报|星瑞格荣获“2022-2023年度国产数据库应用优秀解决方案”奖项
近日,赛迪网为表彰数字赛道上的先行者,联合《数字经济》杂志社和北京科创互联,共同组织以“树立行业标杆,引领服务创新”为中心的“2022-2023年度产业数字服务案例及创新成果征集活动”。该活动旨在鼓励各行业数字化应用技术创新树…...

【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式
【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式 文章目录 【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式一、概述二、什么是幂等性三、幂等性需关注几个重点四、幂等性有什么用五、常见用来保证幂等的手段5.1 MVCC方案5.2 去重表5.3 去重表5.4 select in…...
2023.8.26-2023.9.3 周报【3D+GAN+Diffusion基础知识+训练测试】
目录 学习目标 学习内容 学习时间 学习产出 学习目标 1. 3D方向的基础知识 2. 图像生成的基础知识(GAN \ Diffusion) 3. 训练测试GAN和Diffusion 学习内容 1. 斯坦福cv课程-3D (网课含PPT) 2. sjtu生成模型课件 3. ge…...

如何使用CSS创建渐变阴影?
随着网络的不断发展,制作漂亮的 UI 是提高客户在网站上的参与度的最重要的工作之一。改善前端外观的方法之一是在 CSS 中应用渐变阴影。应用渐变阴影的两种最重要的方法是线性渐变和径向渐变。 渐变阴影可用于吸引用户对特定信息的注意力,应用悬停或焦点…...

perl send HTTP Request
perl send HTTP Request 使用Perl进行发送HttP请求 use LWP::UserAgent; use HTTP::Request; use HTTP::Headers; use JSON::PP;my $test_url "htttp://127.0.0.1:8080/update/";sub sendHttp{my $user_agent LWP::UserAgent->new(timeout>60);my ($url, $…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
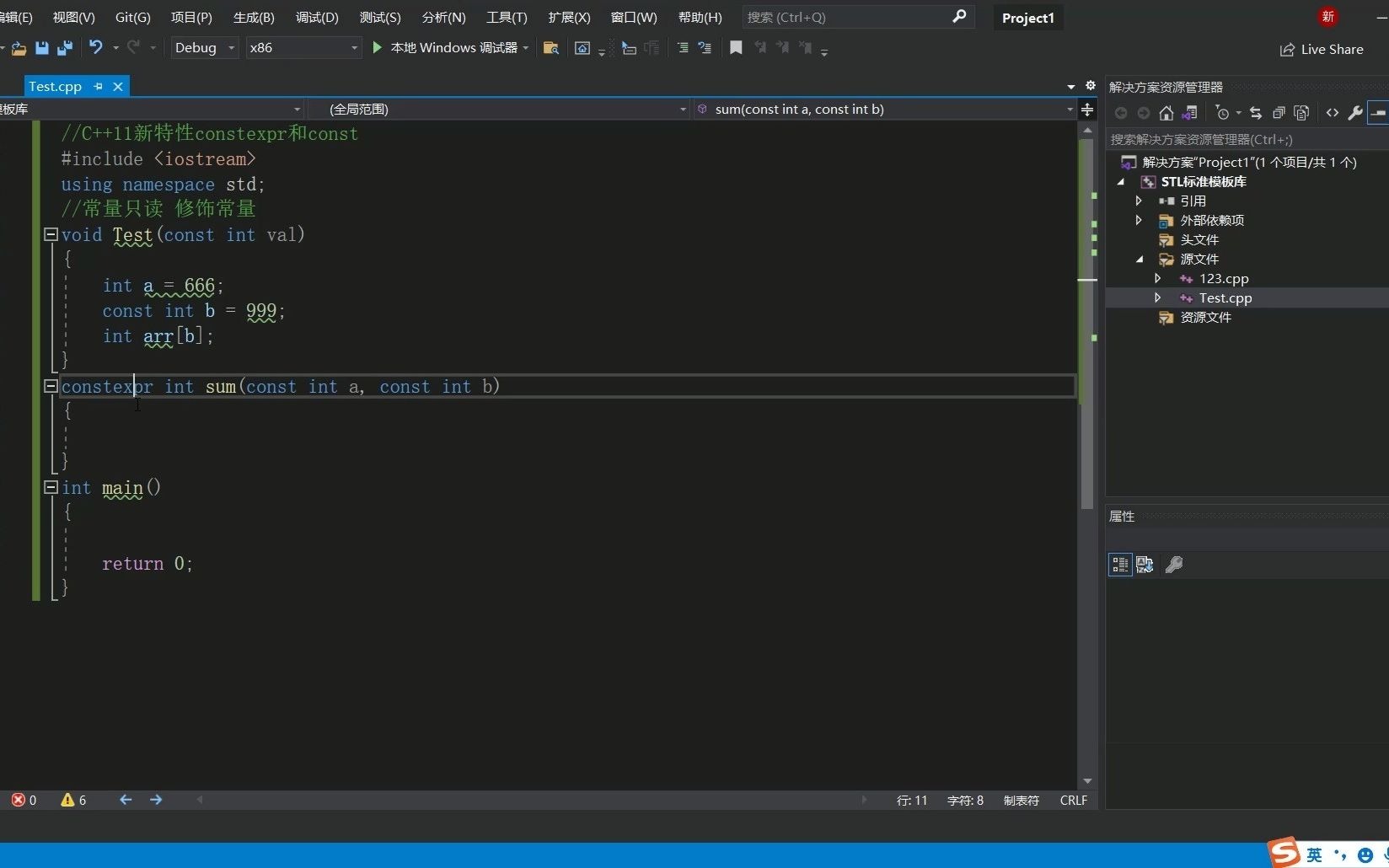
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...
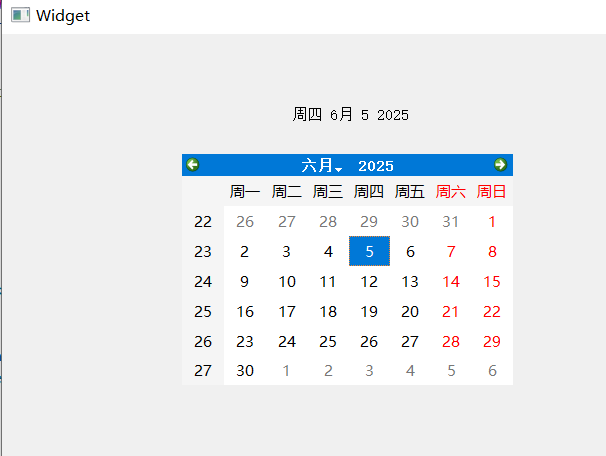
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
