数据结构之树型结构
- 相关概念
- 树的表示
- 二叉树
- 二叉树性质
- 二叉树储存
- 实现一颗二叉树
- 创建
- 遍历(前中后序)
- 获取树中节点个数
- 获取叶子节点个数
- 获取第k层节点个数
- 获取二叉树高度
- 检测值为value元素是否存在
- 层序遍历(需要队列来实现)
- 判断是否为完全二叉树(需要队列来实现)
相关概念
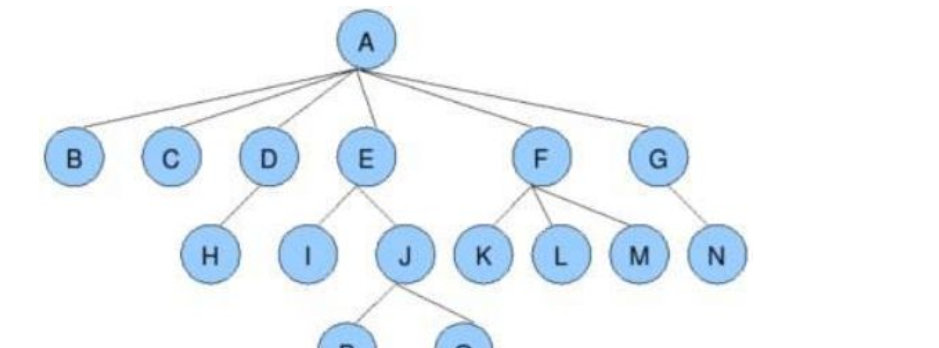
重点概念:后续学习将会反反复复出现

对我们当前学习稍微不重要:

树的表示
树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法(AVL树、红黑树、B树会用到)、孩子兄弟表示法等等。我们了解一下孩子兄弟表示法:
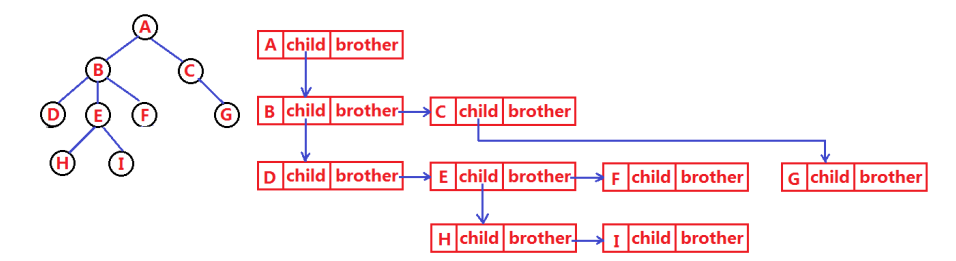
代码表示:
class Node{int value;//我们当前学习就是简简单单的存个int数字Node firstChild;Node nextNorther;}
二叉树
二叉树:每一个节点的度小于等于2;其实就是每一个节点的孩子个数不超过两个。二叉树的有次序是指你把右子树放左边画出来,结果就是两个不同的树
任意二叉树都是由以下的情况组合的:
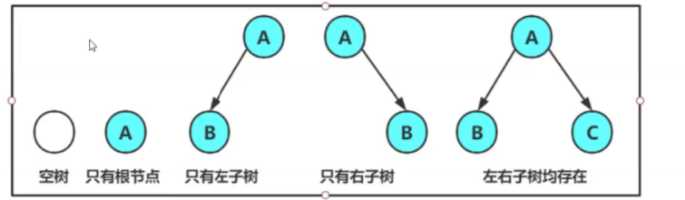
满二叉树:每层的结点数都达到最大值;如果层数是k;满二叉树的节点个数为2^k-1
完全二叉树:你按左右到上下编号1-n一定是连续的
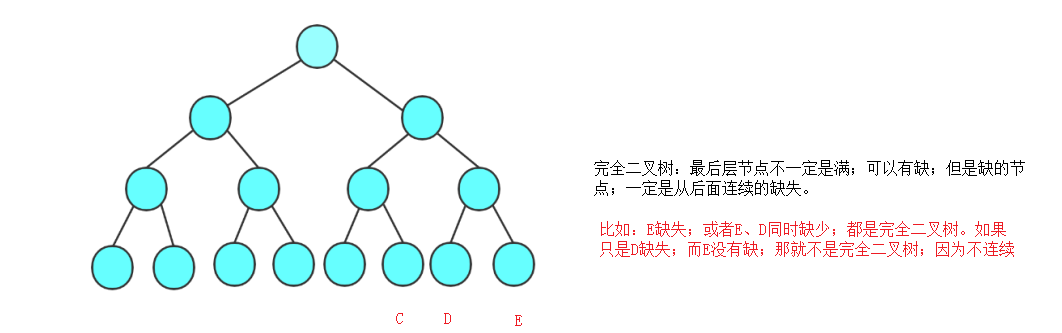
二叉树性质
前提:规定第一层是根节点的二叉树
1:第i层最多节点个数:2^(i-1)
2:深度为k;总节点个数最多是2^k-1 (完全二叉树的情况)
3:非常重要;任意的二叉树;叶子节点个数比度为2的节点个数多一个(度为0就是叶子,不涉及到度为1的节点)
n0=n2+1 (如果要把n1也扯上关系;使用n-1=n00+n11+n2*2;n是总节点个数;解释:一颗n个节点的树有N-1条边;而叶子节点不产生边;度为1的节点只产生一条边;度为2的节点产生两条边)
比如有4层:
其实就是;2的4次方等于2的3次方+2都平方+2的1次方+2的0次方+1。
题目:
某二叉树共有399个结点,其中有199个度为2的结点,则该二叉树中的叶子结点数为()
A不存在这样的二叉树
B200
C198
D199
4:具有n个结点的完全二叉树的深度k为log(n+1)向上取整
不受到你最后层节点个数影响,最后层一个跟2的n-1个是一样,因为用最大节点个数推导出来的
5:对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
注意:完全二叉树度为1的节点要么是1个,要么是0个。奇数个节点就没有度为1的节点,偶数个节点就有一个度为1的节点。如果题目告诉你2n个节点;那就说明有度为1的节点
二叉树储存

如何遍历:
先序:根—>左子树---->右子树(这个比较容易理解)
中序:左子树—>根—>右子树(先访问左子树,然后你左子树又得按照中序进行)
后序:左子树–>右子树—>根
实现一颗二叉树
创建
//创建一颗树
class tree{//树的节点,还是内部类实现,类似链表class Listnode{//一个节点包含三个域char val;Listnode left;//左边Listnode right;//右边public Listnode(char val) {this.val = val;}}public Listnode create(){//先把节点和值创建好,然后再绑关系Listnode A=new Listnode('A');Listnode B=new Listnode('B');Listnode C=new Listnode('C');Listnode D=new Listnode('D');Listnode E=new Listnode('E');Listnode F=new Listnode('F');Listnode G=new Listnode('G');//这里的B和C是节点A.left=B;A.right=C;B.left=D;B.right=E;C.left=F;C.right=G;return A;//返回根节点}遍历(前中后序)
前序:
public void print1(Listnode root){if(root==null) {return ;}System.out.println(root.val);print1(root.left);print1(root.right);}
中序:这次我们就不打印;遍历把值存在顺序表里
public List<Character> print2(Listnode root){List<Character> list=new ArrayList<>();if(root==null){return list;}//System.out.println(root.val);list.add(root.val);print2(root.left);print2(root.right);return list;}
后序:
public List<Character> print3(Listnode root){List<Character> ret=new ArrayList<>();if(root==null){return ret;}//System.out.println(root.val);ret.add(root.val);//先把头放进去,然后左边放一个表,右边放一个表,最后放到retList<Character> s=print3(root.left);ret.addAll(s);List<Character> s1=print3(root.right);ret.addAll(s1);return ret;
}
获取树中节点个数
//获取树中节点的个数int num=0;public int size(Listnode root){//遍历计数器if(root==null) {return 0;}num++;size(root.left);size(root.right);return num;}//子问题计数public int size1(Listnode root){if(root==null) {return 0;}int tmp =size1(root.left)+size1(root.right)+1;//(把走到每个节点都分为左边、右边和它自己)return tmp;}
获取叶子节点个数
// 获取叶子节点的个数int ret3=0;public void getLeafNodeCount(Listnode root){
//自己为空,肯定就结束了if(root==null){return ;}//如果左边和右边同时为空就计数if(root.left==null&&root.right==null){ret3++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);}// 子问题思路-求叶子结点个数public int getLeafNodeCount1(Listnode root){
//自己为空,肯定就结束了if(root==null){return 0;}//如果左边和右边同时为空就计数if(root.left==null&&root.right==null){return 1;}return getLeafNodeCount1(root.left)+getLeafNodeCount1(root.right);}获取第k层节点个数
// 获取第K层节点的个数,直接子问题public int getKLevelNodeCount(Listnode root,int k){
//我们之前不是求了一棵树节点个数吗;假设我要求k层,在k-1的左右子树的和if(root==null||k<=0) {return -1;}if(k==1){//这时候条件就不再是root.left==null&&root.right==null;而是k-1层的孩子节点我都要计算return 1;}int tmp=getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);return tmp;}获取二叉树高度
非常巧妙:递归的结束root==null;返回上一级到叶子节点;发现height1>height2不成立;叶子节点的右边+1;如果是root.left遍历下的就返回给这里的值。画个图就好理解
// 获取二叉树的高度public int getHeight(Listnode root) {if(root==null){return 0;}int height1= getHeight(root.left);int height2= getHeight(root.right);if (height1>height2){return height1+1;//加1是关键,每结束一层+1}elsereturn height2+1;}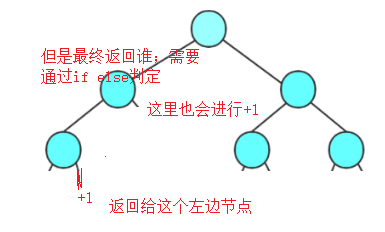
检测值为value元素是否存在
// 检测值为value的元素是否存在public Listnode find(Listnode root, int val) {if (root == null) {return null;}if (root.val == val) {return root;}find(root.left, val);//这里应该把find(root.left,val)存到ret里,避免下面用这个又要重复再递归一次if (find(root.left, val).val == val) {return root;} //如果我在左边找到就不去右边//如果我在右边找到就直接结束,如果都没找到find(root.right, val);if (find(root.right, val).val == val) {return root;}return null;}层序遍历(需要队列来实现)
因为二叉树;没法按这种顺序来遍历;就得依靠别的数据结构

这样子它的打印顺序就是从左到右;画图分析好
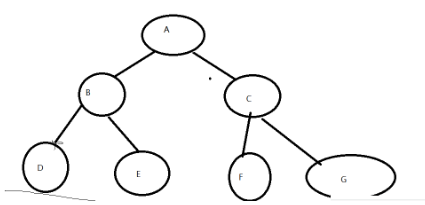
判断是否为完全二叉树(需要队列来实现)
队列;逻辑:按层次遍历弹出,把Null也放入队列里,当弹出Null的时候发现队列全为Null,就说明是完全二叉树
。不全为null就不是完全二叉树。
// 判断一棵树是不是完全二叉树 ,这题逻辑还是非常清晰public boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> qu = new LinkedList<>();qu.offer(root);while (!qu.isEmpty()) {TreeNode cur = qu.poll();if(cur != null) {qu.offer(cur.left);qu.offer(cur.right);}else {break;}}//判断队列剩下的值 是否有 非null的数据while (!qu.isEmpty()) {TreeNode pop = qu.poll();if(pop != null) {return false;}}return true;}
相关文章:

数据结构之树型结构
相关概念树的表示二叉树二叉树性质二叉树储存 实现一颗二叉树创建遍历(前中后序)获取树中节点个数获取叶子节点个数获取第k层节点个数获取二叉树高度检测值为value元素是否存在层序遍历(需要队列来实现)判断是否为完全二叉树&…...
指针进阶详解
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.字符指针 2.指针数组 3.数组指针 4.数组传…...
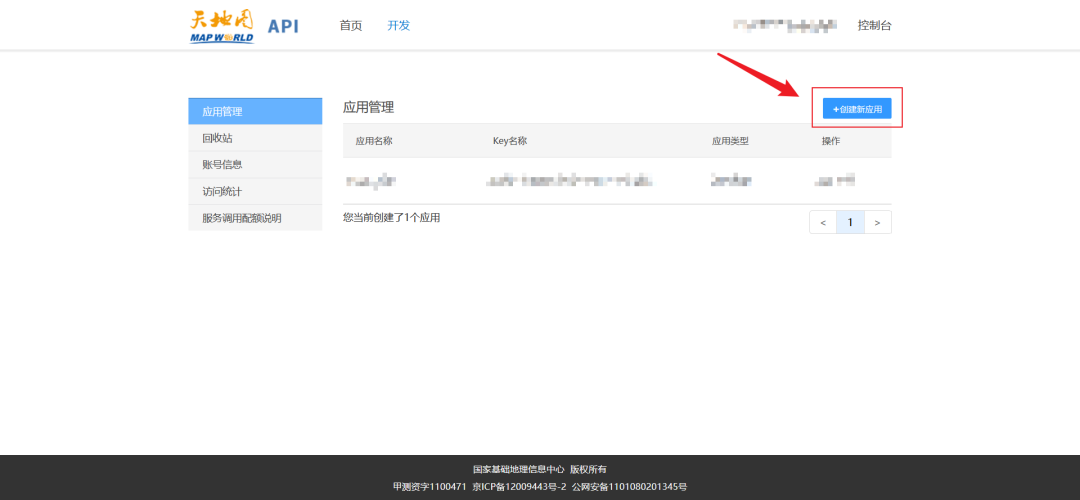
QGIS 如何添加天地图
相信很多小伙伴在 QGIS 里面添加天地图的时候一定感觉很困惑,按照官网的操作申请 Key 之后,添加相对应的服务地址之后看不到地图或者地图不正常显示,今天我们就来解决这个问题 以下所有操作基于 QGIS 3.22 版本 申请 Key 1. 添加天地图的第一步需要申请 Key,首先要注册天…...

PHP8内置函数中的数学函数-PHP8知识详解
php8中提供了大量的内置函数,以便程序员直接使用常见的内置函数包括数学函数、变量函数、字符串函数、时间和日期函数等。今天介绍内置函数中的数学函数。 本文讲到了数学函数中的随机数函数rand()、舍去法取整函数floor()、向上取整函数 ceil()、对浮点数进行四舍…...
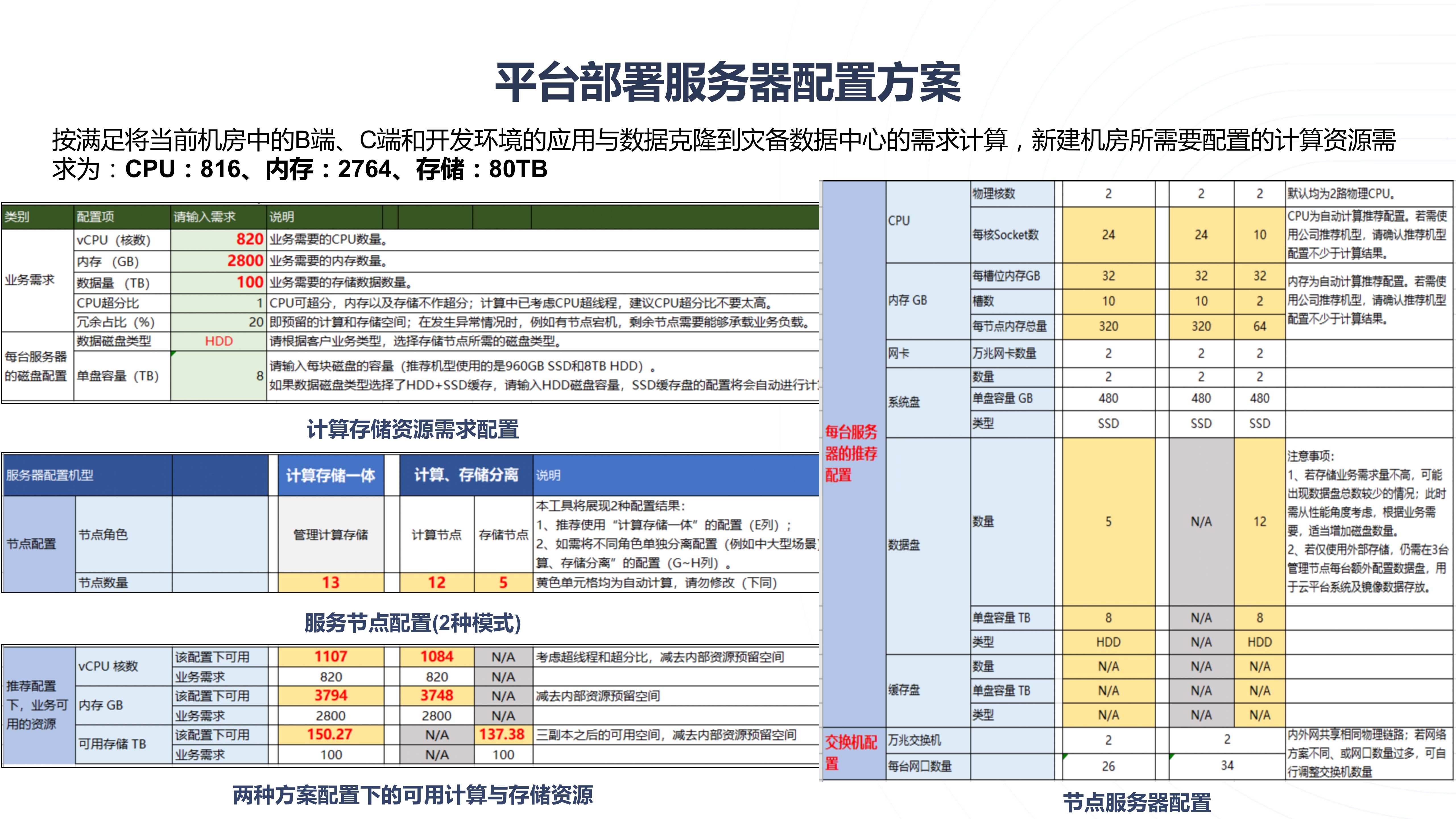
云计算企业私有云平台建设方案PPT
导读:原文《云计算企业私有云平台建设方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 喜欢文章,您可以点赞评论转发本文,…...

ORA-01174: DB_FILES be compatible RAC rolling fashion complete outage
How to change the DB_FILES parameter in RAC (Doc ID 1636681.1)编辑To Bottom In this Document Goal Solution APPLIES TO: Oracle Database - Enterprise Edition - Version 10.1.0.2 and later Oracle Database Cloud Schema Service - Version N/A and later Oracle…...

线性代数(五) 线性空间
前言 《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解 空间是什么 大家较熟悉的:平面直角坐标系是最常见的二维空间 空间由无穷多个坐标点组成 每个坐标点就是一个向量 反过来,也可说&…...
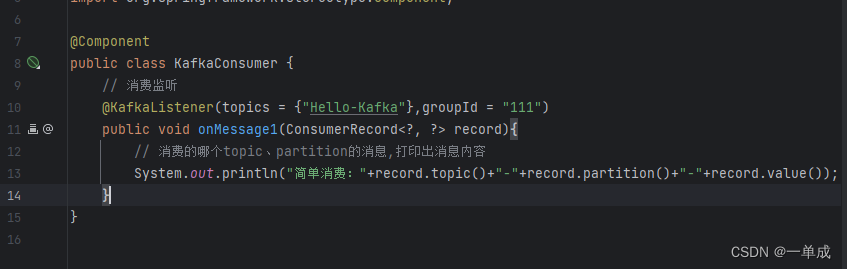
kafka--技术文档--spring-boot集成基础简单使用
阿丹: 查阅了很多资料了解到,使用了spring-boot中整合的kafka的使用是被封装好的。也就是说这些使用其实和在linux中的使用kafka代码的使用其实没有太大关系。但是逻辑是一样的。这点要注意! 使用spring-boot整合kafka 1、导入依赖 核心配…...
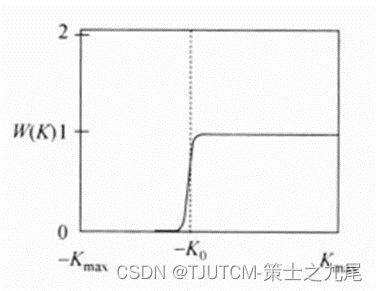
【核磁共振成像】部分傅里叶重建
目录 一、部分傅里叶重建二、部分傅里叶重建算法2.1 填零2.2 零差处理 一、部分傅里叶重建 在部分傅里叶采集中,数据并不是绕K空间中心对称收集的,而是K空间的一半是完全填充的,另一半只收集了一小部分数据。 部分傅里叶采集所依据的原理…...

React中的flushSync与Vue中的nextTick的比较
React中的flushSync与Vue中的nextTick是两种用于处理异步更新的机制。它们在React和Vue这两个流行的前端框架中起着重要的作用。 首先,让我们来看看flushSync。在React中,当需要更新UI时,React会将更新操作放入一个队列中,然后异…...

golang设置国内镜像源
以windows为例, 在cmd 窗口中执行下列语句 go env -w GO111MODULEon go env -w GOPROXYhttps://goproxy.io,direct 或者 1.运行 go env -w GO111MODULEon //开启mod 运行 go env -w GOPROXYhttps://goproxy.cn,direct //设置代理 执…...

linux切换到root没有conda环境
这个错是因为 没有将anaconda添加到环境变量 export PATH"/home/tao/anaconda3/bin:$PATH"然后 source ~/.bashrc或者写入 nano ~/.bashrc在文件的末尾添加以下行 export PATH"/home/tao/anaconda3/bin:$PATH"再 source ~/.bashrc就可以了...

数据库——redis介绍
文章目录 redis是什么?分布式缓存常见的技术选型方案有哪些?说一下 Redis 和 Memcached 的区别和共同点? redis是什么? 简单来说 Redis 就是一个使用 C 语言开发的数据库,不过与传统数据库不同的是 Redis 的数据是存在…...
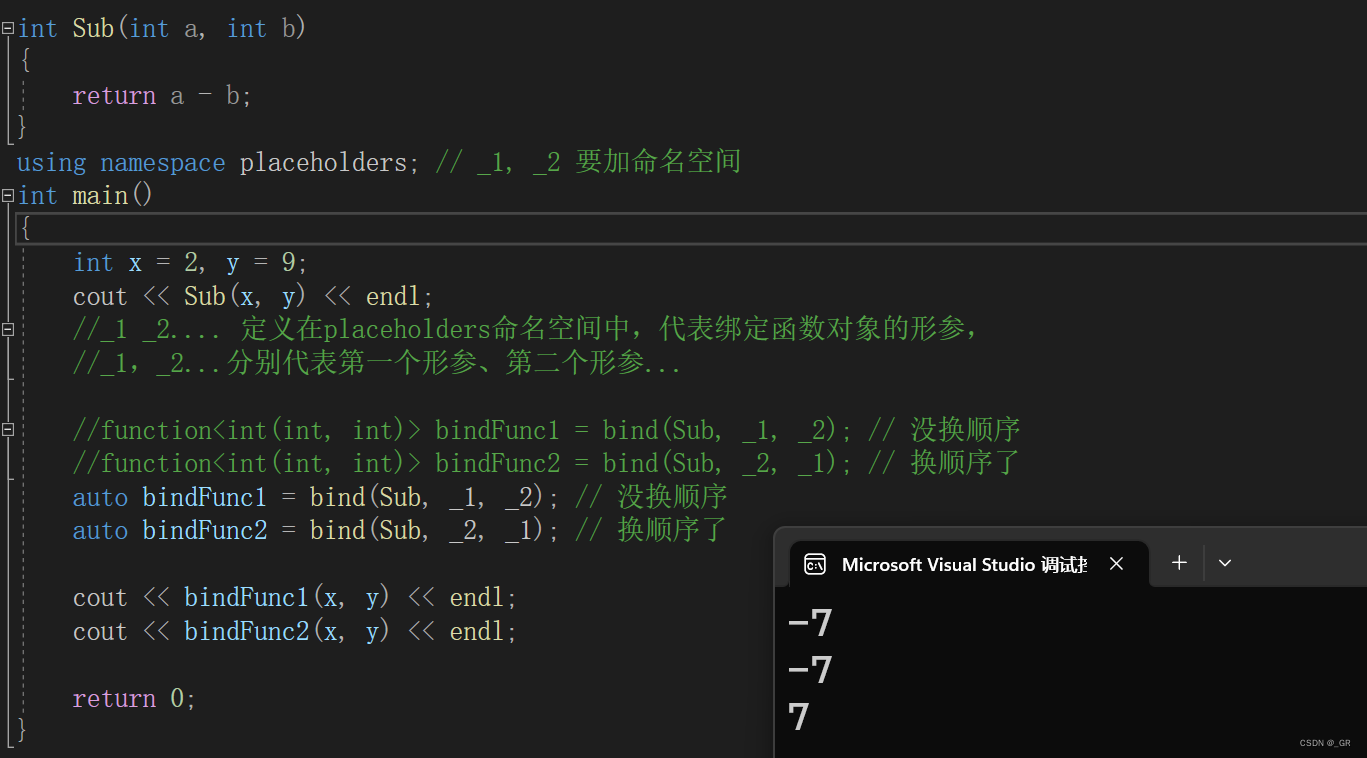
从C语言到C++_34(C++11_下)可变参数+ lambda+function+bind+笔试题
目录 1. 可变参数模板 1.1 展开参数包 1.1.1 递归函数方式展开 1.1.2 逗号表达式展开 1.2 emplace相关接口 2. lambda表达式(匿名函数) 2.1 C11之前函数的缺陷 2.2 lambda表达式语法 2.3 函数对象与lambda表达式 3. 包装器 3.1 function包装器…...

喜报|星瑞格荣获“2022-2023年度国产数据库应用优秀解决方案”奖项
近日,赛迪网为表彰数字赛道上的先行者,联合《数字经济》杂志社和北京科创互联,共同组织以“树立行业标杆,引领服务创新”为中心的“2022-2023年度产业数字服务案例及创新成果征集活动”。该活动旨在鼓励各行业数字化应用技术创新树…...

【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式
【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式 文章目录 【Spring Cloud系列】- 分布式系统中实现幂等性的几种方式一、概述二、什么是幂等性三、幂等性需关注几个重点四、幂等性有什么用五、常见用来保证幂等的手段5.1 MVCC方案5.2 去重表5.3 去重表5.4 select in…...
2023.8.26-2023.9.3 周报【3D+GAN+Diffusion基础知识+训练测试】
目录 学习目标 学习内容 学习时间 学习产出 学习目标 1. 3D方向的基础知识 2. 图像生成的基础知识(GAN \ Diffusion) 3. 训练测试GAN和Diffusion 学习内容 1. 斯坦福cv课程-3D (网课含PPT) 2. sjtu生成模型课件 3. ge…...

如何使用CSS创建渐变阴影?
随着网络的不断发展,制作漂亮的 UI 是提高客户在网站上的参与度的最重要的工作之一。改善前端外观的方法之一是在 CSS 中应用渐变阴影。应用渐变阴影的两种最重要的方法是线性渐变和径向渐变。 渐变阴影可用于吸引用户对特定信息的注意力,应用悬停或焦点…...

perl send HTTP Request
perl send HTTP Request 使用Perl进行发送HttP请求 use LWP::UserAgent; use HTTP::Request; use HTTP::Headers; use JSON::PP;my $test_url "htttp://127.0.0.1:8080/update/";sub sendHttp{my $user_agent LWP::UserAgent->new(timeout>60);my ($url, $…...
阿里云CDN缓存预热与刷新以及常见的故障汇总
文章目录 1.为CDN缓存的文件增加过期时间2.CDN缓存预热配置3.CDN缓存刷新配置4.常见故障 CDN缓存预热指的是主动将要缓存的文件推送到全国各地的CDN边缘加速器上,减少回源率,提供命中率。 缓存刷新指的是后期上传了同名的文件,之前的缓存已经…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
