代码随想录打卡—day45—【DP】— 8.29 完全背包应用
1 70. 爬楼梯(完全背包版)
70. 爬楼梯
完全背包+装满的选法+排列的套路,AC代码:
class Solution {
public:/*完全背包的思路:1 2是两个物体 可以无限取*/int dp[50]; // 能爬到第i楼的选法的排列数/*dp[j] += dp[j - i];dp[0] = 1for容积j++ for物体i++ 排列+无限个模拟——n=3*/int climbStairs(int n) {dp[0] = 1;for(int j = 0; j <= n; j++)for(int i = 1; i <= 2; i++) //物体if(j >= i)dp[j] += dp[j - i];// for(int i = 1; i <= 2; i++)// {// for(int j = 0; j <= n; j++)// cout << tmp[i][j] << ' ';// puts("");// }return dp[n];}
};2 322. 零钱兑换
322. 零钱兑换
之前做过,直接看这篇
3 279. 完全平方数
279. 完全平方数
之前没学多重背包之前看到题目是蒙的,现在学完时候很自然就做出来了,AC代码:
class Solution {
public:int dp[10010]; // dp[1]表示 凑成i的完全平方数最少需要的数目/*转成完全背包物品:i = 1....sqrt(n)背包:ndp[j] = min(dp[j- i]+1,dp[j])装i 不撞idp[0] = 0 其他非0下标全设为INT_MAXi++j++模拟——*/int numSquares(int n) {dp[0] = 0;for(int j = 1; j <= n; j++)dp[j] = INT_MAX;for(int i = 1; i*i <= n; i++){for(int j = 0; j <= n; j++){if(j >= i*i)dp[j] = min(dp[j- i*i]+1,dp[j]);else dp[j] = dp[j];}// for(int j = 0; j <= n; j++) cout << dp[j] << ' ';// puts("");}return dp[n];}
};相关文章:

代码随想录打卡—day45—【DP】— 8.29 完全背包应用
1 70. 爬楼梯(完全背包版) 70. 爬楼梯 完全背包装满的选法排列的套路,AC代码: class Solution { public:/*完全背包的思路:1 2是两个物体 可以无限取*/int dp[50]; // 能爬到第i楼的选法的排列数/*dp[j] dp[j - i];dp[0] 1fo…...
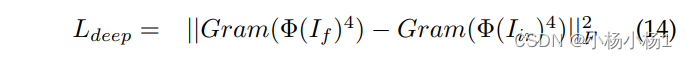
2023.8.28日论文阅读
文章目录 NestFuse: An Infrared and Visible Image Fusion Architecture based on Nest Connection and Spatial/Channel Attention Models(2020的论文)本文方法 LRRNet: A Novel Representation Learning Guided Fusion Network for Infrared and Visible Images本文方法学习…...
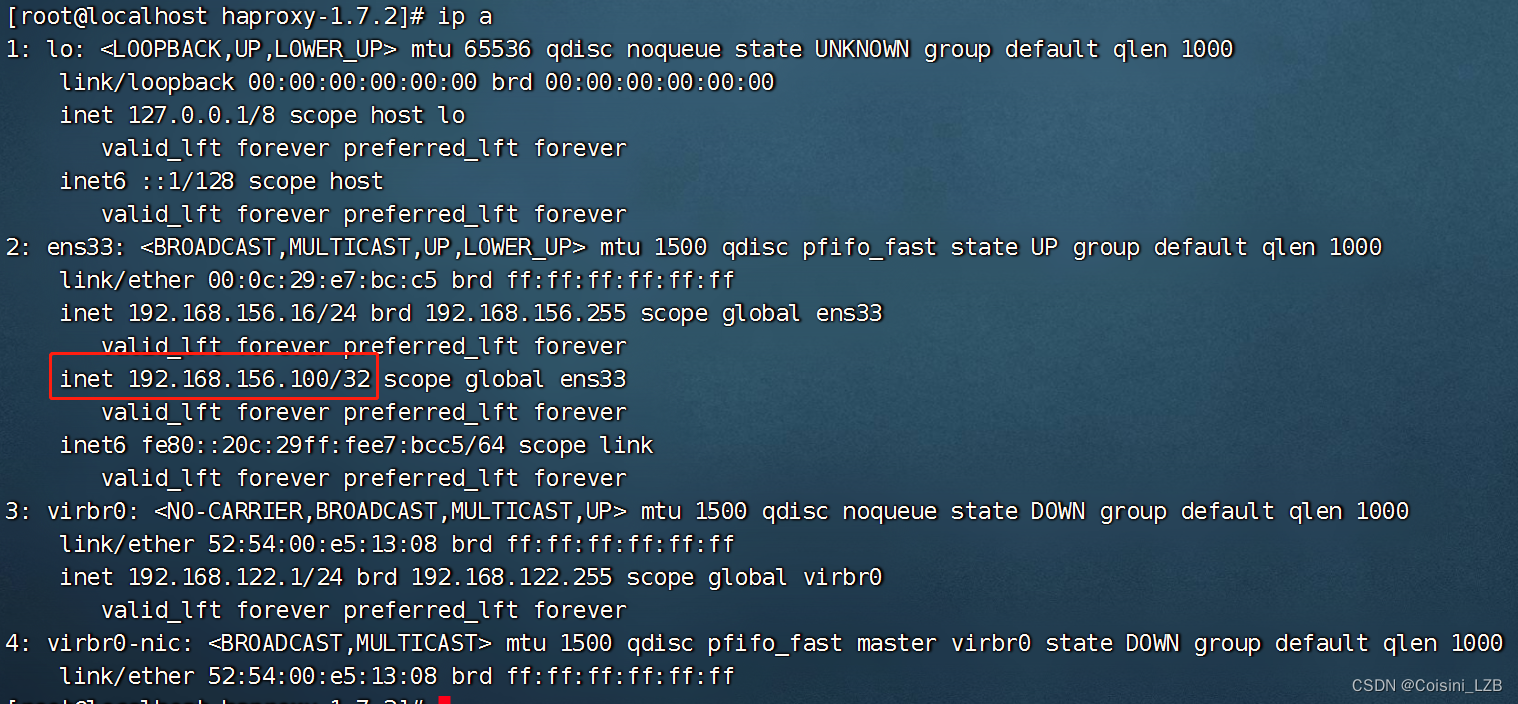
HAproxy(四十七)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、概述 1.1 简介 1.2 核心功能 1.3 关键特性 1.4 应用场景 二、安装 1.内核配置 2.编译安装 3. 建立配置文件 4. 添加为系统服务 5. 添加3和5运行级别下自启动…...

Java实战场景下的ElasticSearch
文章目录 前言一、环境准备二、RsetAPI操作索引库1.创建索引库2.判断索引库是否存在3.删除索引库 二、RsetAPI操作文档1.新增文档2.单条查询3.删除文档4.增量修改5.批量导入6.自定义响应解析方法 四、常用的查询方法1.MatchAll():查询所有2.matchQuery():单字段查询3.multiMatc…...

拓世科技集团 | “书剑人生”李步云学术思想研讨会暨李步云先生九十华诞志庆
2023年,中国改革开放迎来了45周年,改革春风浩荡,席卷神州大地,45年间,中国特色社会主义伟大事业大步迈入崭新境界,一路上结出了饶为丰硕的果实。中华民族在这45年间的砥砺前行,不仅使中国的经济…...

前端须知名词解释
目录 一、多维转一维 二、一维转多维 一维转多维——使用场景:分页 三、判断当前元素是否为数组 四、判断当前元素是否是空对象 五、数字分割符:提高数字可读性 六、模糊盒子(怪异盒子)与标准盒模型 七、css的filter属性 …...

React性能优化之memo缓存函数
React是一个非常流行的前端框架,但是在处理大型应用程序时,性能可能会成为一个问题。为了解决这个问题,React提供了一个称为memo的功能,它可以缓存函数并避免不必要的重新渲染。 memo是React中的一个高阶组件(HOC&…...

2023年高教社杯 国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
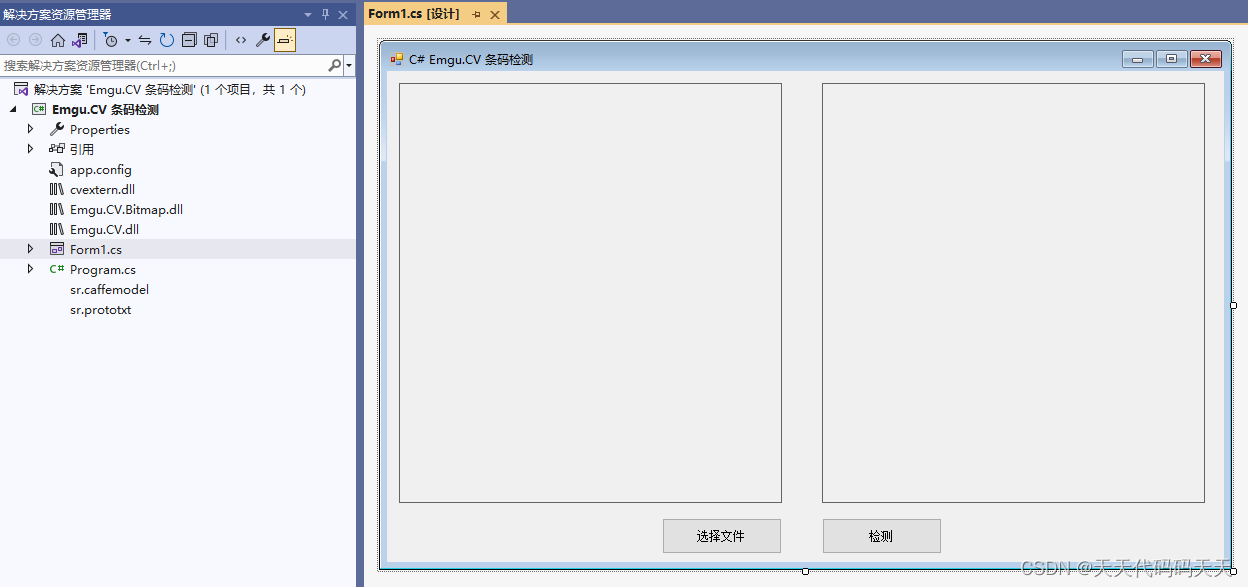
C# Emgu.CV 条码检测
效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using Emgu.CV; using Emgu.CV.Util; using static Emgu.C…...

VueRouter的基本使用
路由的基本使用 文章目录 路由的基本使用01-VueRouterVueRouter的使用 ( 5 2)综合代码 拓展:组件存放问题 什么是路由呢? 在生活中的路由:设备和IP的映射关系 在Vue中:路径 和 组件 的 映射 关系。 01-Vu…...

网工笔记:快速认识7类逻辑接口
逻辑接口是指能够实现数据交换功能但物理上不存在、需要通过配置建立的接口。逻辑接口需要承担业务传输。 下面是我整理了7款常见的逻辑接口。 接口类型 描述 Eth-Trunk接口 具有二层特性和三层特性的逻辑接口,把多个以太网接口在逻辑上等同于一个逻辑接口&…...
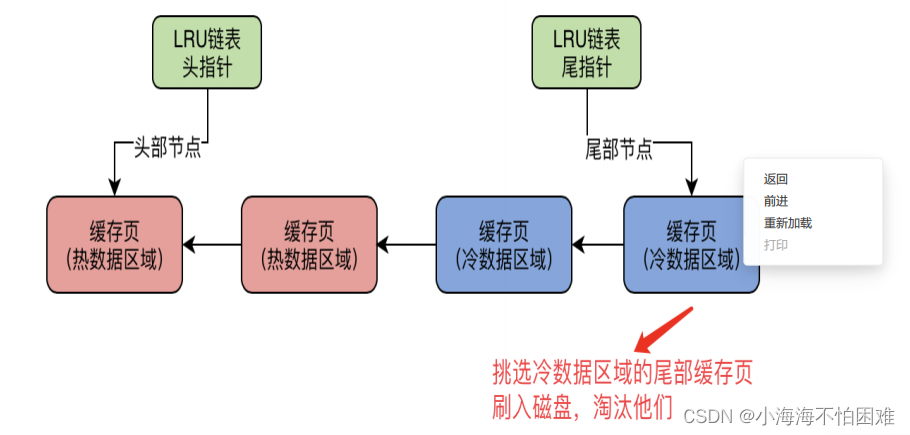
MySQL中的free链表,flush链表,LRU链表
一、free链表 1、概述 free链表是一个双向链表数据结构,这个free链表里,每个节点就是一个空闲的缓存页的描述数据块的地址,也就是说,只要你一个缓存页是空闲的,那么他的描述数据块就会被放入这个free链表中。 刚开始数…...
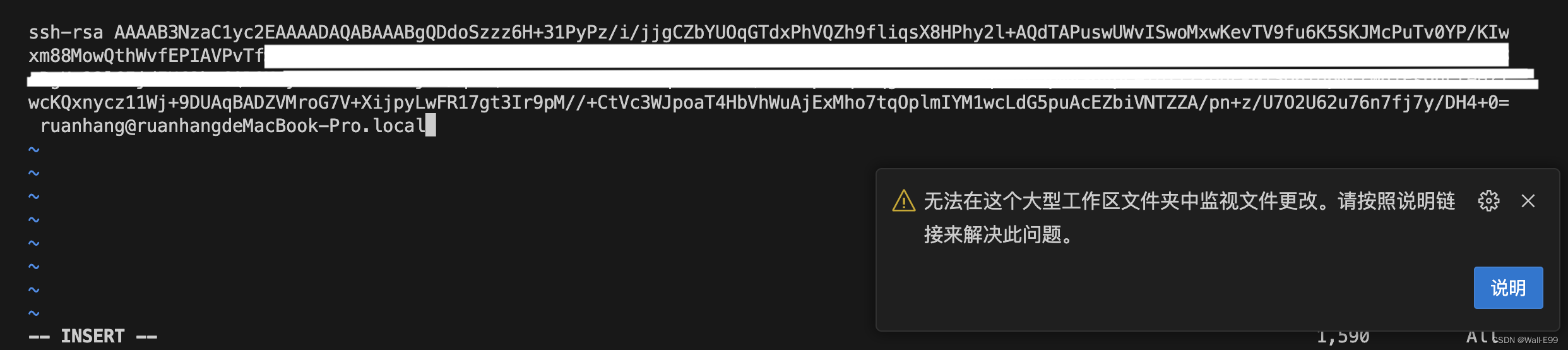
mac使用VsCode远程连接服务器总是自动断开并要求输入密码的解决办法
在mac中使用vscode远程连接服务器,时常会出现自动断开并要求重新输入服务器密码的问题,接下来让我们来解决它: 1、首先,在本地创建公钥: ssh-keygen 这条命令执行之后,出现提示直接回车即可;直…...

Python爬虫分布式架构 - Redis/RabbitMQ工作流程介绍
在大规模数据采集和处理任务中,使用分布式架构可以提高效率和可扩展性。本文将介绍Python爬虫分布式架构中常用的消息队列工具Redis和RabbitMQ的工作流程,帮助你理解分布式爬虫的原理和应用。 为什么需要分布式架构? 在数据采集任务中&#…...
【ES】笔记-集合介绍与API
集合是一种不允许值重复的顺序数据结构。 通过集合我们可以进行并集、交集、差集等数学运算, 还会更深入的理解如何使用 ECMAScript 2015(ES2015)原生的 Set 类。 构建数据集合 集合是由一组无序且唯一(即不能重复)的项组成的。该数据结构使用了与有限集合相同的数…...
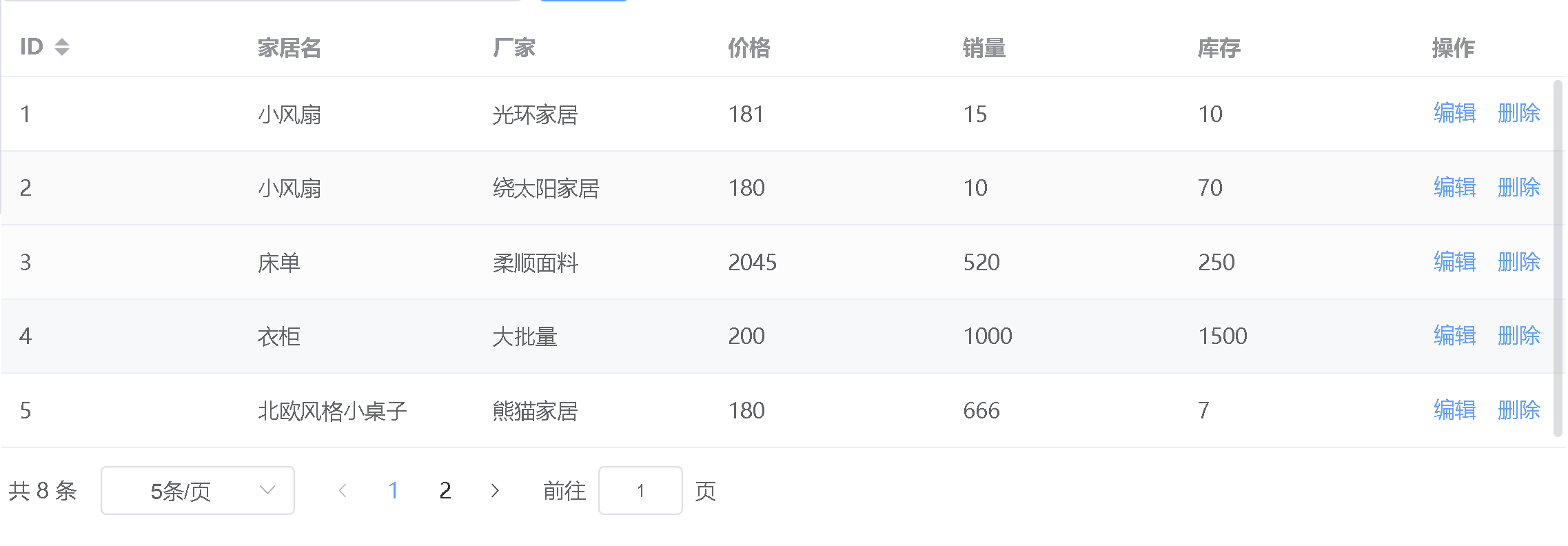
Spring Boot(Vue3+ElementPlus+Axios+MyBatisPlus+Spring Boot 前后端分离)【五】
😀前言 本篇博文是关于Spring Boot(Vue3ElementPlusAxiosMyBatisPlusSpring Boot 前后端分离)【五】,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章…...

二、Tomcat 安装集
一、Tomcat—Docker 1. 拉取镜像 # 1、拉取镜像(tomcat版本8,jre版本8)。 docker pull tomcat:8-jre82. 启动容器 # 2、启动一个tomcat容器。 docker run -id --name tomcat -p 8080:8080 镜像ID # 3、宿主机里新建/root/tomcat目录&#x…...

CentOS 上通过 NFS 挂载远程服务器硬盘
NFS(Network File System)是一种用于在不同的计算机系统之间共享文件和目录的协议。它允许一个计算机系统将其文件系统的一部分或全部内容暴露给其他计算机系统,使其能够像访问本地文件一样访问这些内容。在这篇博客中,我们将介绍…...

微信小程序中的 广播监听事件
定义 WxNotificationCenter.js 文件; /*** author: Di (微信小程序开发工程师)* organization: WeAppDev(微信小程序开发论坛)(http://weappdev.com)* 垂直微信小程序开发交流社区* * github地址: https://github.com/icindy/WxNotificationCenter…...

Quickstart: MinIO for Linux
单节点部署教程 1.安装Minio服务端 //wget下载二进制文件 wget https://dl.min.io/server/minio/release/linux-amd64/minio //赋予权限 chmod x minio //将minio可执行文件移入usr/local/bin目录下,使得minio可以全局执行 sudo mv minio /usr/local/bin/ 2.启动Mi…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
