2023年高教社杯 国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
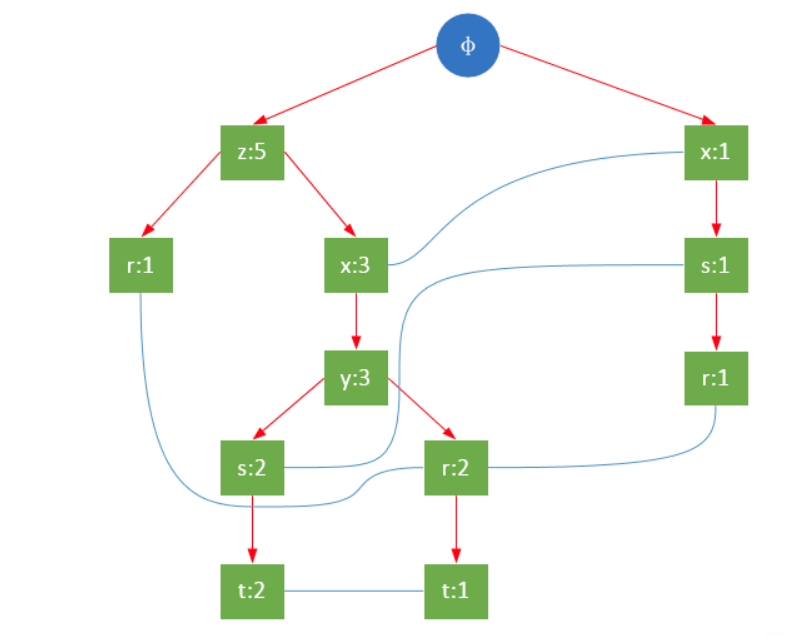
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
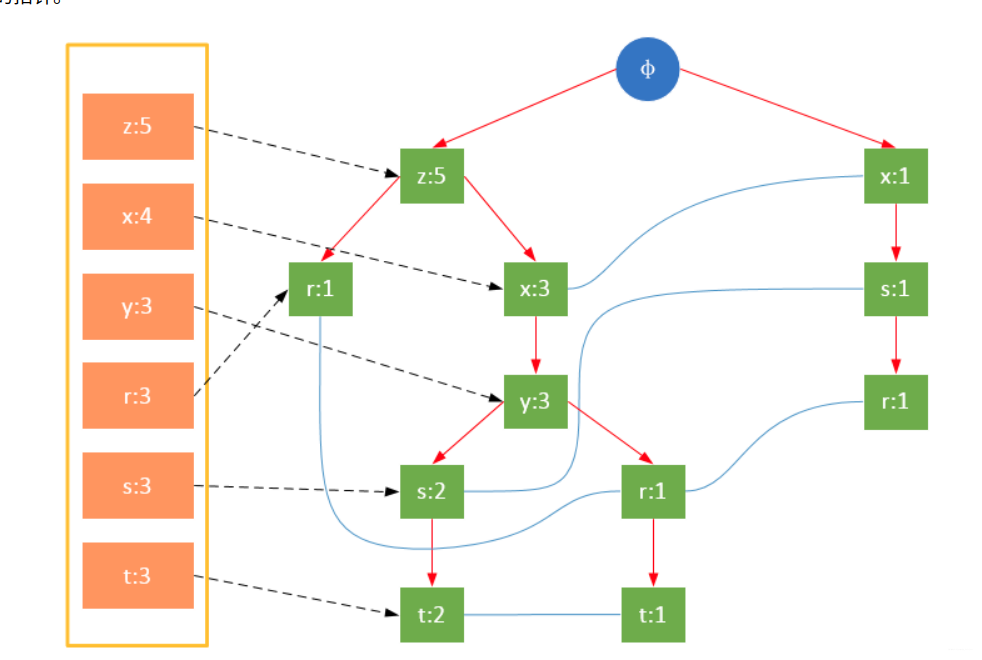
3 构建FP树
现在有如下数据:
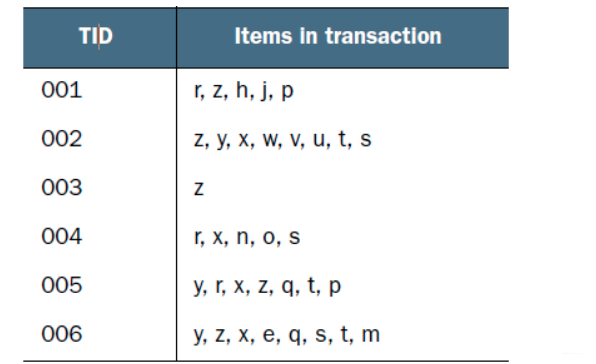
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
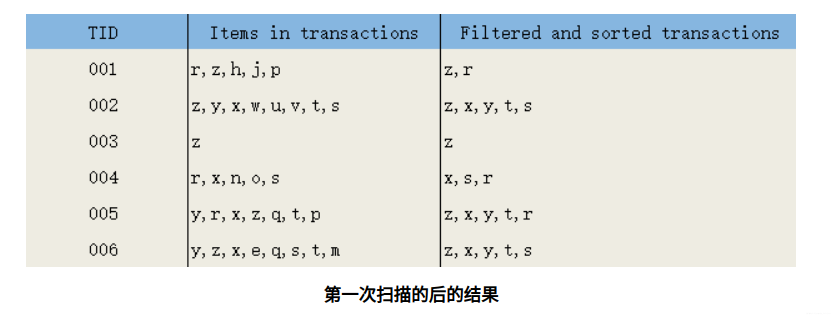
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
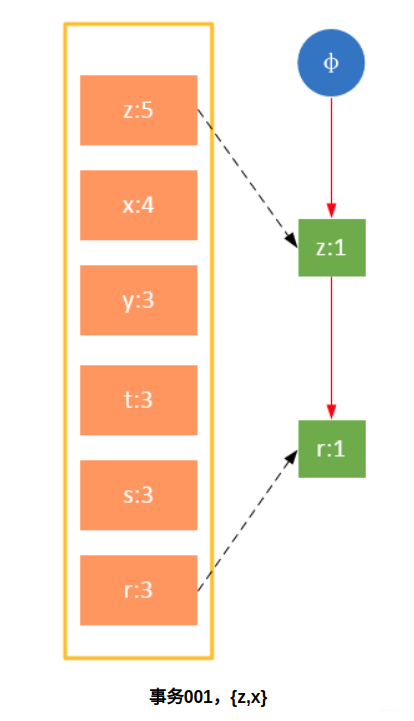
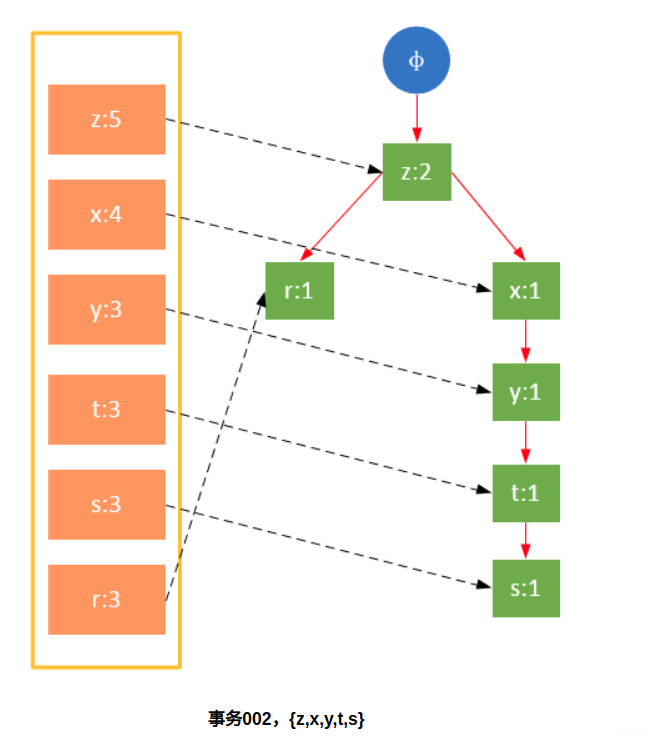
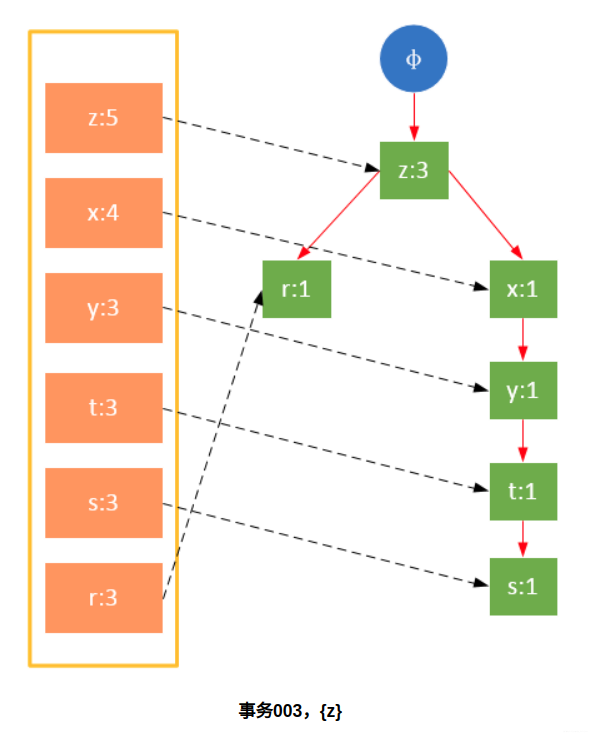
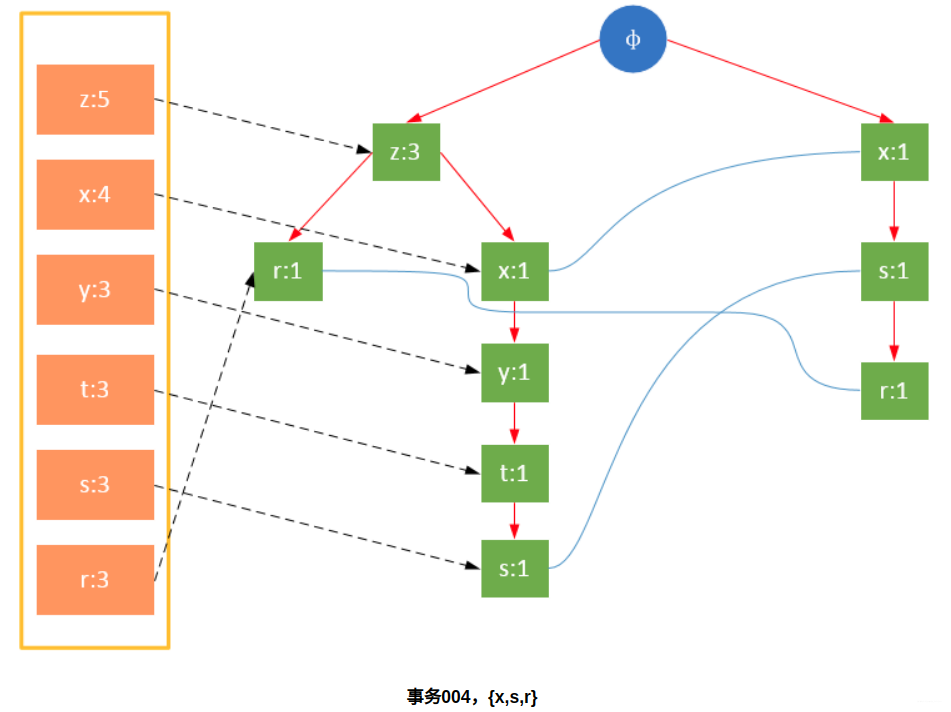
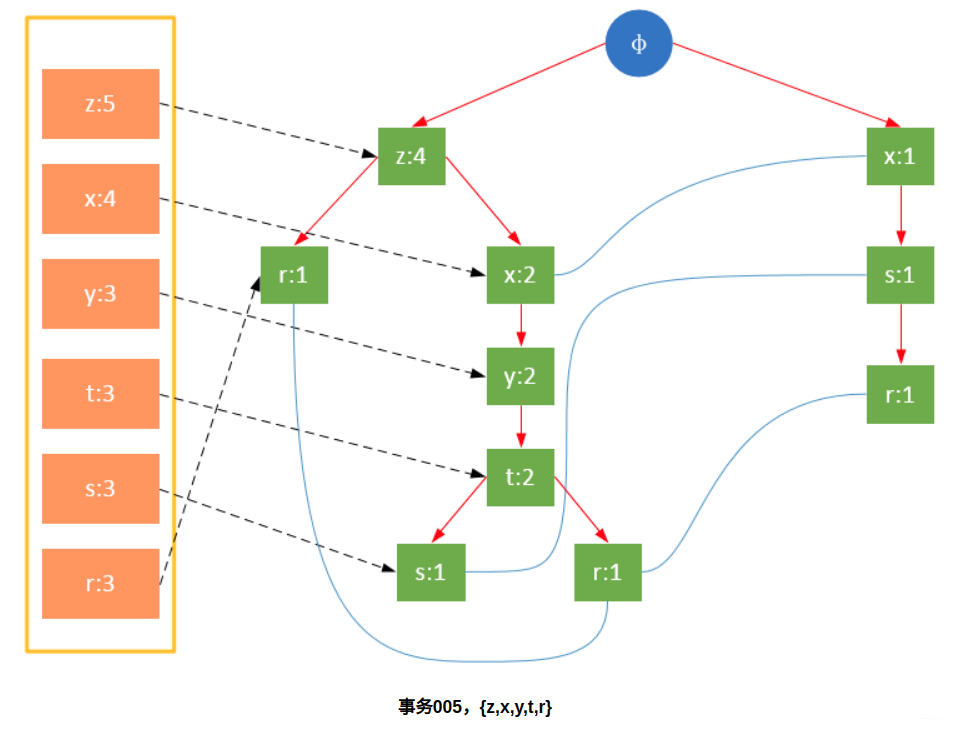
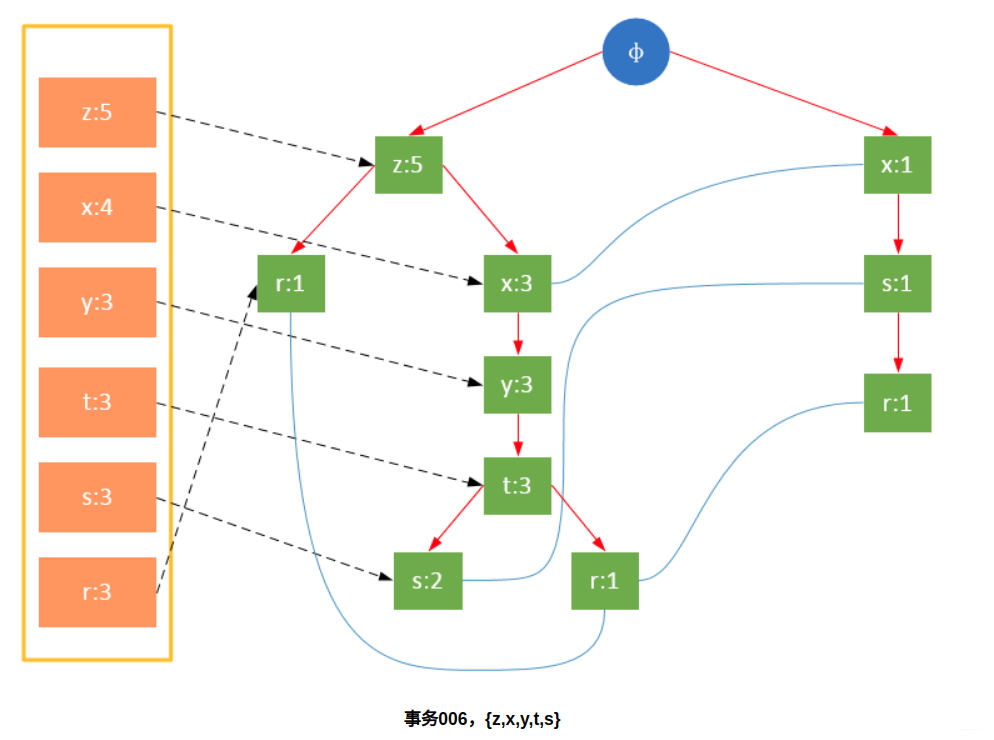
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯 国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
C# Emgu.CV 条码检测
效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using Emgu.CV; using Emgu.CV.Util; using static Emgu.C…...

VueRouter的基本使用
路由的基本使用 文章目录 路由的基本使用01-VueRouterVueRouter的使用 ( 5 2)综合代码 拓展:组件存放问题 什么是路由呢? 在生活中的路由:设备和IP的映射关系 在Vue中:路径 和 组件 的 映射 关系。 01-Vu…...

网工笔记:快速认识7类逻辑接口
逻辑接口是指能够实现数据交换功能但物理上不存在、需要通过配置建立的接口。逻辑接口需要承担业务传输。 下面是我整理了7款常见的逻辑接口。 接口类型 描述 Eth-Trunk接口 具有二层特性和三层特性的逻辑接口,把多个以太网接口在逻辑上等同于一个逻辑接口&…...
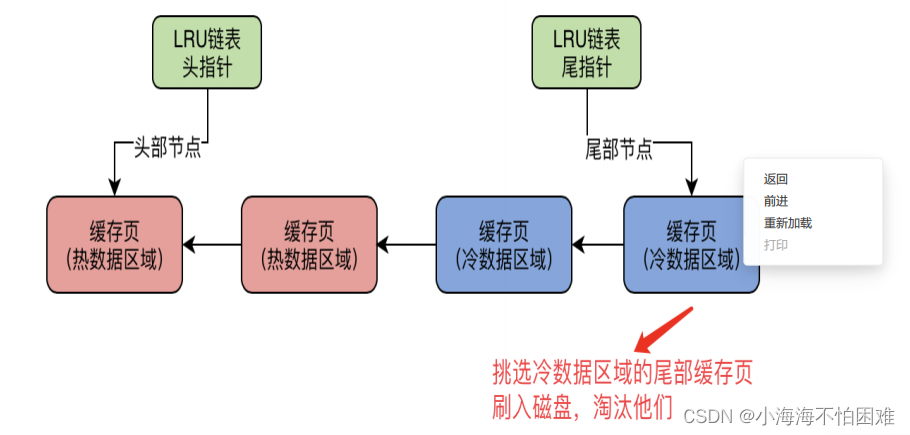
MySQL中的free链表,flush链表,LRU链表
一、free链表 1、概述 free链表是一个双向链表数据结构,这个free链表里,每个节点就是一个空闲的缓存页的描述数据块的地址,也就是说,只要你一个缓存页是空闲的,那么他的描述数据块就会被放入这个free链表中。 刚开始数…...
mac使用VsCode远程连接服务器总是自动断开并要求输入密码的解决办法
在mac中使用vscode远程连接服务器,时常会出现自动断开并要求重新输入服务器密码的问题,接下来让我们来解决它: 1、首先,在本地创建公钥: ssh-keygen 这条命令执行之后,出现提示直接回车即可;直…...

Python爬虫分布式架构 - Redis/RabbitMQ工作流程介绍
在大规模数据采集和处理任务中,使用分布式架构可以提高效率和可扩展性。本文将介绍Python爬虫分布式架构中常用的消息队列工具Redis和RabbitMQ的工作流程,帮助你理解分布式爬虫的原理和应用。 为什么需要分布式架构? 在数据采集任务中&#…...
【ES】笔记-集合介绍与API
集合是一种不允许值重复的顺序数据结构。 通过集合我们可以进行并集、交集、差集等数学运算, 还会更深入的理解如何使用 ECMAScript 2015(ES2015)原生的 Set 类。 构建数据集合 集合是由一组无序且唯一(即不能重复)的项组成的。该数据结构使用了与有限集合相同的数…...
Spring Boot(Vue3+ElementPlus+Axios+MyBatisPlus+Spring Boot 前后端分离)【五】
😀前言 本篇博文是关于Spring Boot(Vue3ElementPlusAxiosMyBatisPlusSpring Boot 前后端分离)【五】,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章…...

二、Tomcat 安装集
一、Tomcat—Docker 1. 拉取镜像 # 1、拉取镜像(tomcat版本8,jre版本8)。 docker pull tomcat:8-jre82. 启动容器 # 2、启动一个tomcat容器。 docker run -id --name tomcat -p 8080:8080 镜像ID # 3、宿主机里新建/root/tomcat目录&#x…...

CentOS 上通过 NFS 挂载远程服务器硬盘
NFS(Network File System)是一种用于在不同的计算机系统之间共享文件和目录的协议。它允许一个计算机系统将其文件系统的一部分或全部内容暴露给其他计算机系统,使其能够像访问本地文件一样访问这些内容。在这篇博客中,我们将介绍…...

微信小程序中的 广播监听事件
定义 WxNotificationCenter.js 文件; /*** author: Di (微信小程序开发工程师)* organization: WeAppDev(微信小程序开发论坛)(http://weappdev.com)* 垂直微信小程序开发交流社区* * github地址: https://github.com/icindy/WxNotificationCenter…...

Quickstart: MinIO for Linux
单节点部署教程 1.安装Minio服务端 //wget下载二进制文件 wget https://dl.min.io/server/minio/release/linux-amd64/minio //赋予权限 chmod x minio //将minio可执行文件移入usr/local/bin目录下,使得minio可以全局执行 sudo mv minio /usr/local/bin/ 2.启动Mi…...
Java中word转Pdf工具类
背景: 最近做的一个项目中,对于word转Pdf用的地方很多,特此记录 搭建总图: 代码部分: 1.需要的jar包: aspose-words-15.8.0-jdk16.jar 注:下载好这个jar包后,在项目的根目录新建一…...

【conda install】网络慢导致报错CondaHTTPError: HTTP 000 CONNECTION FAILED for url
⭐⭐问题: 部署安装环境经常会出现由于网络慢问题,导致conda安装不了库,报错如下: Solving environment: failedCondaHTTPError: HTTP 000 CONNECTION FAILED for url <https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/…...
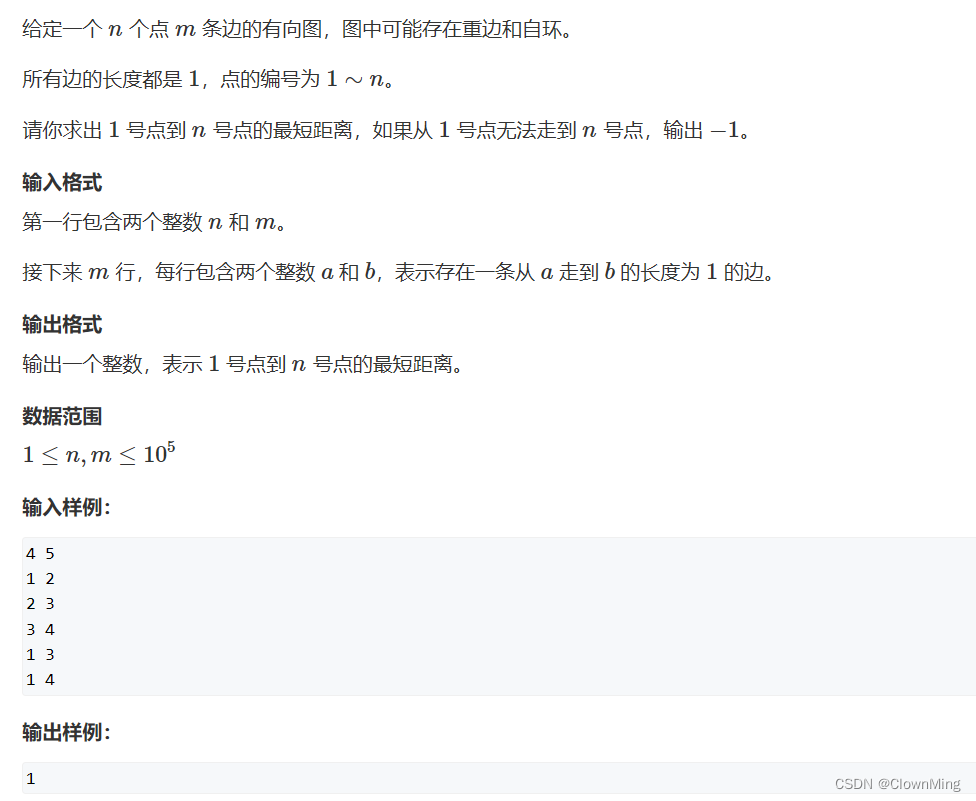
2023-8-28 图中点的层次(树与图的广度优先遍历)
题目链接:图中点的层次 #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 100010;int h[N], e[N], ne[N], idx; int n, m; int q[N], d[N];void add(int a, int b) {e[idx] b, ne[idx] h[a], h…...
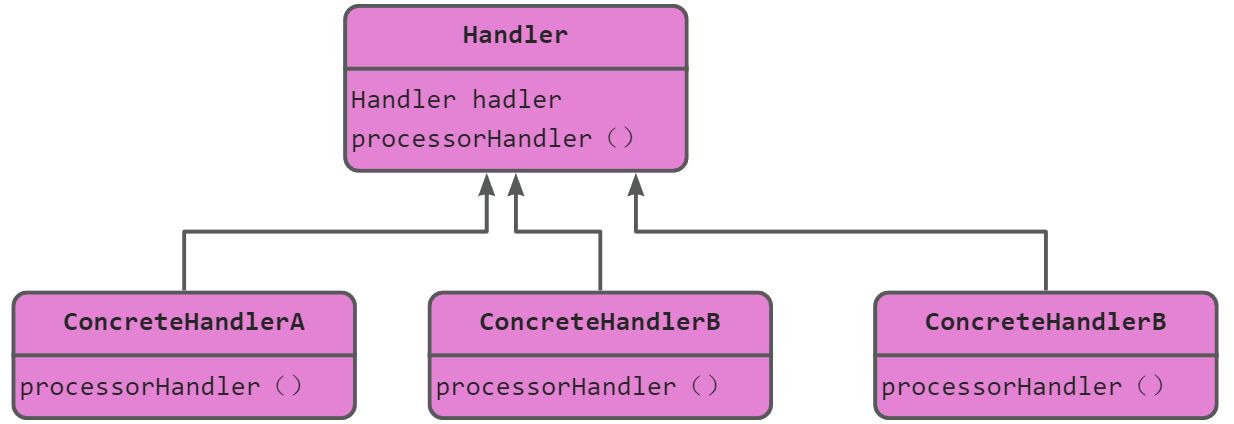
设计模式(一)
1、适配器模式 (1)概述 适配器中有一个适配器包装类Adapter,其包装的对象为适配者Adaptee,适配器作用就是将客户端请求转化为调用适配者中的接口;当调用适配器中的方法时,适配器内部会调用适配者类的方法…...
Prometheus关于微服务的监控
在微服务架构下随着服务越来越多,定位问题也变得越来越复杂,因此监控服务的运行状态以及针对异常状态及时的发出告警也成为微服务治理不可或缺的一环。服务的监控主要有日志监控、调用链路监控、指标监控等几种类型方式,其中指标监控在整个微服务监控中比重最高,也是实际生…...

CSS实现白天/夜晚模式切换
目录 功能介绍 示例 原理 代码 优化 总结 功能介绍 在网页设计和用户体验中,模式切换功能是一种常见的需求。模式切换可以为用户提供不同的界面外观和布局方案,以适应其个人偏好或特定环境。在这篇博客中,我们将探索如何使用纯CSS实现一…...

selenium实现输入数字字母验证码
思路 1. 登录url 2. 获取验证码坐标 3. 根据桌标截图验证码 4. 对验证码进行识别 5. 自动输入验证码 测试代码 import os import time from io import BytesIO from PIL import Image from selenium import webdriver from selenium.webdriver.common.by import By impo…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
