Mysql--技术文档--B树-数据结构的认知
阿丹解读:
B+树(B+ tree)和B树(B-tree)都是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。
基本概念-B+树/B树
B树(B-tree)和B+树(B+ tree)是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。它们具有一些共同的基本概念:
-
节点(Node):B树和B+树的数据存储在节点中。节点可以包含多个关键字和对应的指针。在B树中,叶子节点和内部节点的结构相同,都存储数据和关键字。而在B+树中,叶子节点只存储关键字和指向数据的指针,而内部节点存储关键字和指向子节点的指针。
-
关键字(Key):关键字是B树和B+树中用于对数据进行排序和搜索的值。关键字按照升序排列,并被存储在节点中。
-
指针(Pointer):指针用于连接节点,形成树的结构。在B树和B+树中,指针可以指向子节点、父节点或兄弟节点,实现树的平衡。
-
根节点(Root Node):根节点是B树和B+树的顶层节点。它是树的起点,通过根节点可以访问到整个树的结构。
-
叶节点(Leaf Node):叶节点是树的最底层节点。在B树中,叶节点存储数据和关键字。而在B+树中,叶节点只存储关键字和指向数据的指针。叶节点之间通过指针进行连接,形成一个有序的双向链表。
-
内部节点(Internal Node):内部节点是B树和B+树中非叶节点。它们用于指向子节点,并存储关键字。
B树和B+树作为自平衡的搜索树,具有增删改查的操作,每次操作后都会进行平衡以保持树的高度接近最小值。这样可以确保查询效率的稳定性,并提供高效的范围查询和区间搜索能力。
以上是B树和B+树的基本概念,它们在实际应用中有着广泛的应用,尤其在数据库和文件系统中用于管理和查找大量数据。
B树
B树(B-tree)是一种自平衡的搜索树数据结构,被广泛应用于数据库和文件系统等领域。它具有高效的查找、插入和删除操作,适合在磁盘上存储和检索大量数据。
B树的工作原理如下:
-
根节点:B树的顶层节点称为根节点。根节点可以有多个子节点,且关键字的数量和子节点的数量相等。
-
关键字有序存储:在B树中,节点内的关键字按照升序排列,并且关键字的数量决定了节点的最大容量。
-
节点分裂:当往一个节点插入关键字时,如果节点已满,将会进行分裂。分裂会将关键字分为两部分,并生成两个新节点。
-
子节点指针:除了关键字,节点还会存储指向子节点的指针。子节点指针的数量比关键字的数量多一个。
通过上述原理,B树可以实现快速的查找、插入和删除操作。
B树的性能优点包括:
-
减少磁盘访问:B树的节点尺寸一般较大,可以容纳更多的关键字。这样可以减少磁盘IO的次数,提高数据读写的效率。
-
平衡性:B树会在插入和删除操作后进行节点的自平衡,使树的高度保持相对较小。这样可以保持查询效率的稳定性。
-
范围查询:由于B树中的关键字有序存储,范围查询和区间搜索变得高效。可以通过节点的查找和遍历实现范围查询。
-
适应多层存储:B树的设计使其适用于多层存储系统,如内存和磁盘。节点的容量可以根据不同层级的存储进行调整,适应不同的场景。
需要注意的是,B树的具体性能表现会受到节点容量、节点分裂策略和具体实现等因素的影响。在实际应用中,可以根据具体的需求和场景选择合适的B树参数和配置,以获得更好的性能和效果。
B树的复杂度
| 平均 | 最差 | |
|---|---|---|
| 空间复杂度 | O(n) | O(n) |
| 搜索 | O(log n) | O(log n) |
| 插入 | O(log n) | O(log n) |
| 删除 | O(log n) | O(log n) |
B树工作流程
提供一个网址可手动看见树的工作流程
B-Tree Visualization
流程图
详解工作流程
查找
流程描述:
-
从根节点开始,在当前节点中查找是否存在目标关键字。如果存在,查找成功并返回相应的数据。
-
如果目标关键字小于当前节点的最小关键字,则转到该节点的最左子节点进行下一步查找。
-
如果目标关键字大于当前节点的最大关键字,则转到该节点的最右子节点进行下一步查找。
-
如果目标关键字在当前节点关键字的范围内(大于等于最小关键字且小于等于最大关键字),则根据关键字的大小选择合适的子节点,并进入下一层继续查找。
-
重复以上步骤,直到在某个叶子节点中找到目标关键字,或者在某个节点中无法找到目标关键字。
图示流程:

插入
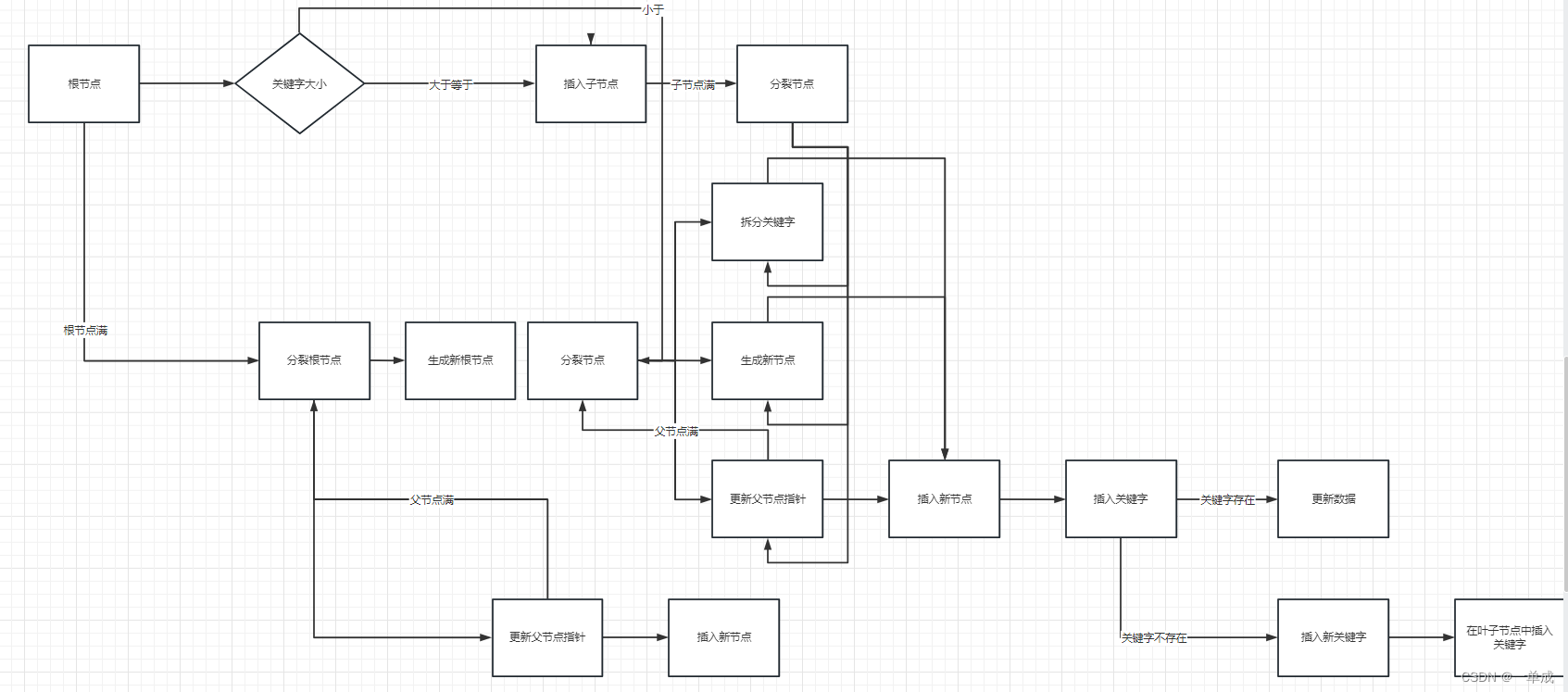
插入代码需要根据具体情况来进行拆分
单层容量满需要分裂
当插入元素后发现元素已经超过了阶数,则需要向上拆分
在B树中,当插入元素导致某层节点的容量已满时,需要进行节点的分裂操作。分裂操作会将该节点的关键字分为两部分,并生成两个新节点。拆分的规则如下:
-
拆分关键字:假设插入前节点中的关键字按升序排列,在容量已满的节点中,将关键字分为两部分。前一部分的关键字留在原节点,后一部分的关键字移至新节点。通常,中间位置的关键字作为拆分点,可以平均分配关键字给两个新节点。
-
更新指针:拆分节点后,需要更新相关的指针。对于内部节点,拆分后,新节点的关键字会大于原节点中的所有关键字,将新节点的指针链接到原节点的右侧。对于叶子节点,拆分后,新节点将成为原节点的右兄弟节点,并与原节点进行指针连接。
-
提升拆分点:当拆分点是根节点中的关键字时,拆分后的两个新节点会成为新的根节点,原根节点的指针指向这两个新节点。
通过上述规则,B树在容量已满时进行节点的分裂,以维持树的平衡性。拆分后,树的高度可能增加,但通过平衡操作可以保持树的高度接近最小值。
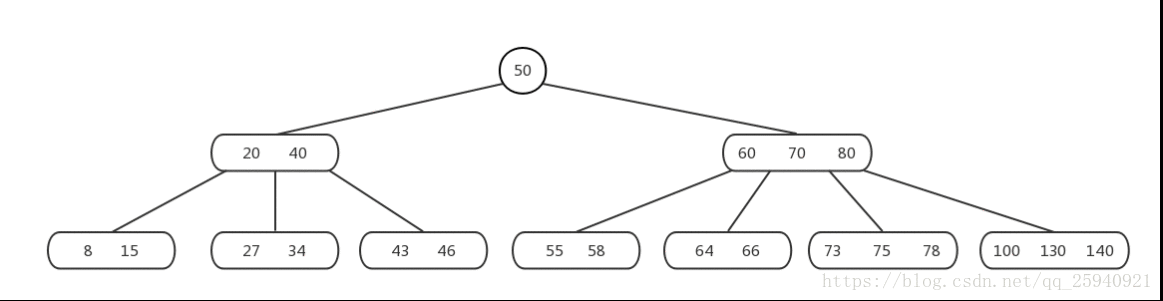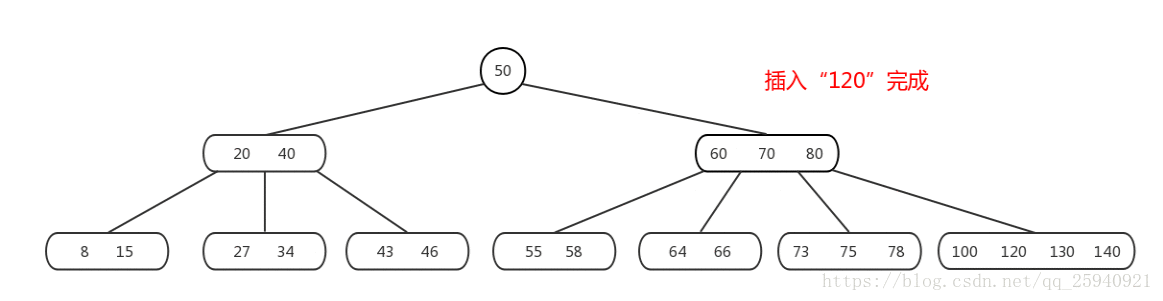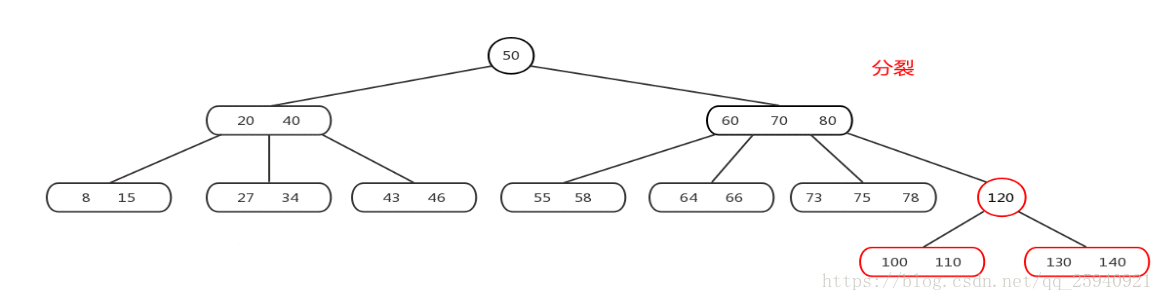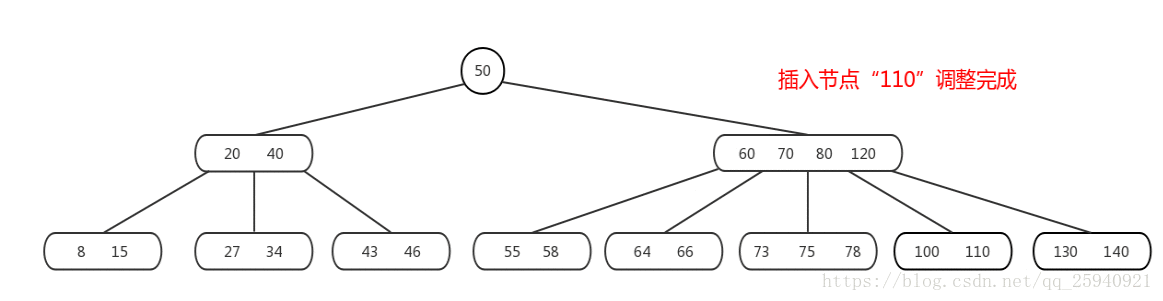
多层容量满需要分裂
当多层层次的节点容量满时,B树在插入操作时的流程如下:
-
从根节点开始,在当前节点中查找插入位置。如果要插入的关键字已经存在,可能会更新相应的数据,否则,将关键字插入到当前节点。
-
如果当前节点已满,进行节点的分裂操作。拆分的规则如前面所述,将关键字分为两部分,并生成两个新节点。对于内部节点,拆分后,新节点的关键字会大于原节点中的所有关键字,将新节点插入到原节点父节点的相应位置。对于叶子节点,拆分后,新节点将成为原节点的右兄弟节点,并进行指针的连接。
-
分裂操作可能会导致上层节点容量变满,需要再次进行分裂。如果分裂的节点是根节点,将生成新的根节点,并将原根节点作为新根节点的子节点。
-
重复以上步骤,不断向上进行节点的分裂操作,直到遇到非满节点或者根节点。
-
如果根节点满了,进行根节点的分裂,并生成新的根节点。根节点分裂会导致B树的高度增加,但也保持了树的平衡。
重点:从顶向下进行分裂!!!
整体插入流程图
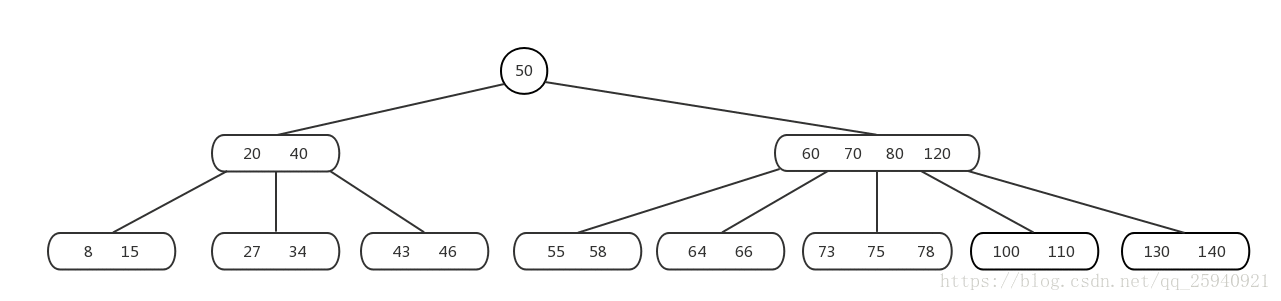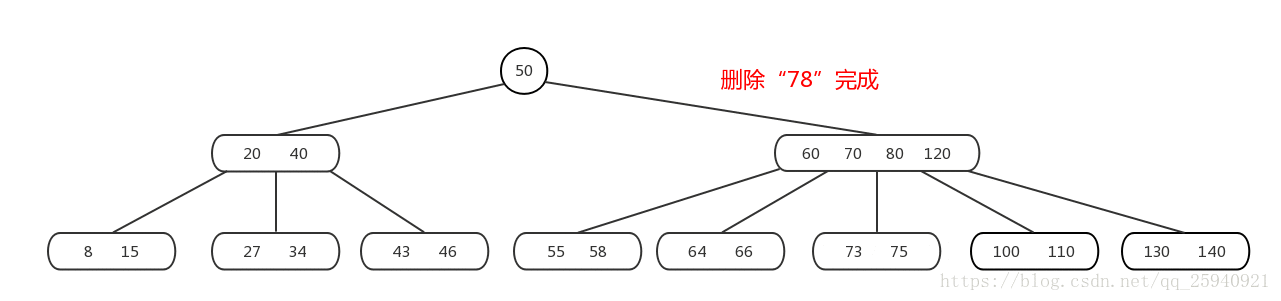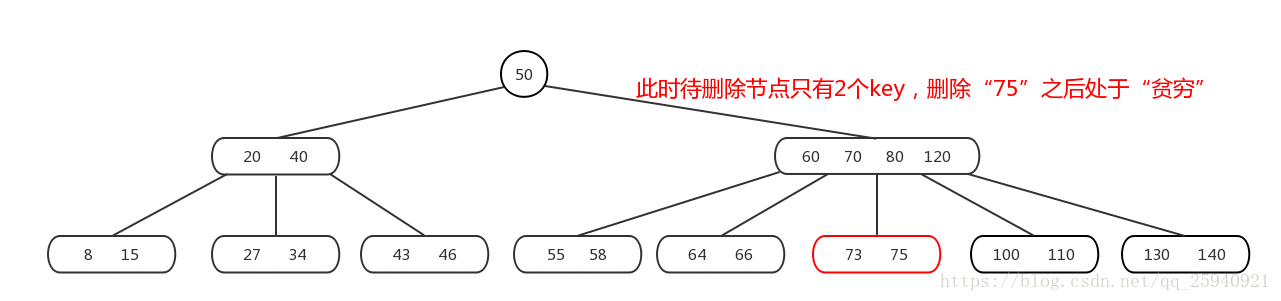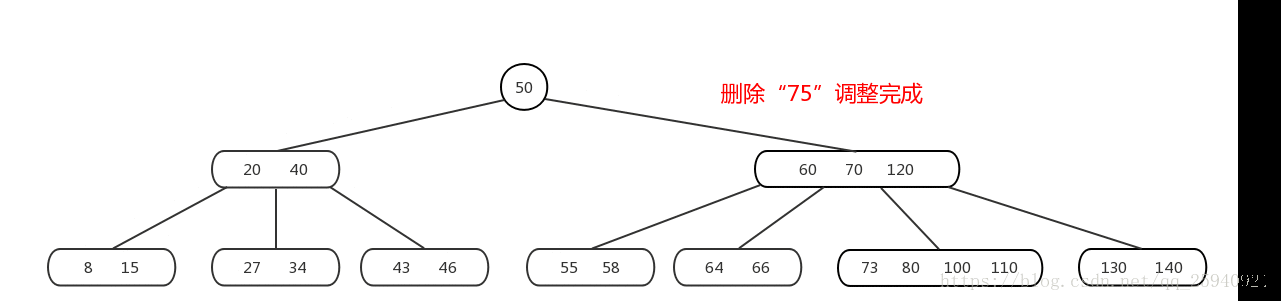
删除
删除有两个相关的基本操作:合并和填充
合并操作:是值将两个子节点合并为一个子节点;
填充操作:指删除元素后,当一个节点中元素个数小于最小元素个数时,需要向此节点中填充元素。在填充操作的时候需要调用合并操作。
合并操作流程:
-
找到需要合并的两个相邻子节点。
-
选择一个关键字从父节点中下来填充合并后的子节点。这个关键字可以是两个相邻子节点之间的父节点关键字,或者是子节点中的一个关键字。
-
将两个子节点中的关键字和指针合并到一个新的子节点中。合并后的子节点将成为原两个子节点的父节点连接的子节点。
-
更新父节点的关键字和指针,将被合并的子节点移除,并将合并后的子节点添加到父节点中。
-
如果父节点关键字数量小于最小关键字数量,可能需要继续进行合并操作,直到满足平衡条件。
通过合并操作,B树可以保持平衡性,并保证树的高度接近最小值。当删除一个关键字导致节点关键字数量不满足要求时,合并操作可以将多个子节点合并为一个节点,减少节点数量以提高空间利用率。
图示:

删除操作流程:
B树的删除工作流程如下:
-
从根节点开始,在当前节点中查找要删除的关键字。如果关键字存在于当前节点,则执行删除操作。
-
如果要删除的关键字在当前节点中不存在,根据关键字的大小选择合适的子节点,并进入下一层继续查找与删除操作。
-
如果要删除的关键字在叶子节点中找到,直接删除该关键字。
-
如果要删除的关键字在内部节点中找到,则可以选择使用前驱或后继关键字代替要删除的关键字。一般情况下,选择后继关键字进行替换。
-
如果替换后的关键字所在的节点关键字数量小于最小关键字数量,则可能需要进行合并和填充操作,以保持树的平衡。
-
合并操作:如果替换后的关键字所在的节点的兄弟节点关键字数量大于最小关键字数量,可以选择从兄弟节点中借一个关键字过来,或者进行合并操作。
-
填充操作:如果替换后的关键字所在的节点的兄弟节点关键字数量也小于等于最小关键字数量,则可能需要进行填充操作。填充操作可能需要借一个关键字过来,或者通过合并操作将当前节点与兄弟节点合并。
-
重复以上步骤,直到在某个叶子节点中找到要删除的关键字,或者确定不存在要删除的关键字。
通过上述流程,B树可以实现删除操作,并保持树的平衡和性能。删除操作可能会触发合并和填充操作,以优化节点的利用率和树的结构。需要注意的是,B树的删除操作可以涉及多次的合并和填充操作,以保持树的平衡。
重点概念与流程:
合并操作:
在B树中,合并操作是指将两个子节点合并为一个子节点的操作。当一个节点中的关键字数量小于最小关键字数量时,可以执行合并操作。
合并操作的工作流程如下:
-
找到需要合并的两个相邻子节点。
-
选择一个关键字从父节点中下来填充合并后的子节点。这个关键字可以是两个相邻子节点之间的父节点关键字,或者是子节点中的一个关键字。
-
将两个子节点中的关键字和指针合并到一个新的子节点中。合并后的子节点将成为原两个子节点的父节点连接的子节点。
-
更新父节点的关键字和指针,将被合并的子节点移除,并将合并后的子节点添加到父节点中。
-
如果父节点关键字数量小于最小关键字数量,可能需要继续进行合并操作,直到满足平衡条件。
通过合并操作,B树可以保持平衡性,并保证树的高度接近最小值。当删除一个关键字导致节点关键字数量不满足要求时,合并操作可以将多个子节点合并为一个节点,减少节点数量以提高空间利用率。
合并策略:
在B树中,合并操作的合并策略通常有以下几种:
-
左兄弟合并:首先尝试将当前节点与其左兄弟节点进行合并。合并后,当前节点的关键字会被移动到左兄弟节点,并与左兄弟节点的关键字合并。这种合并策略会保持原有节点的顺序性。
-
右兄弟合并:如果左兄弟合并失败或左兄弟节点不存在,可以尝试将当前节点与其右兄弟节点进行合并。合并后,当前节点的关键字会被移动到右兄弟节点,并与右兄弟节点的关键字合并。这种合并策略同样会保持原有节点的顺序性。
-
中间位置合并:如果左兄弟合并和右兄弟合并都失败或兄弟节点不存在,可以考虑合并两个相邻的子节点中的中间位置的关键字。该关键字可以是父节点关键字中的一个,或者是两个子节点中的某个关键字。此合并策略可能会调整节点的顺序性,因为中间关键字可能会被移动到新的合并节点中。
通过以上合并策略,可以选择合适的方式将两个子节点合并为一个节点。合并操作会减少B树中的节点数量以提高空间利用率,同时还有助于保持树的平衡性。
B树的默认合并策略通常会优先选择左兄弟合并或右兄弟合并
填充操作:
填充操作的流程如下:
-
在进行填充操作之前,需要先确定当前节点关键字数量小于最小关键字数量,并确定要进行填充的节点。
-
首先查找当前节点的兄弟节点,找出关键字数量大于最小关键字数量的兄弟节点。
-
如果存在兄弟节点,可以选择从兄弟节点中借一个关键字过来填充当前节点。这可以通过从兄弟节点中移动一个关键字和相应的指针到当前节点来实现。
-
更新父节点的关键字和指针,以及兄弟节点的关键字和指针,完成填充操作。
-
如果不存在关键字数量大于最小关键字数量的兄弟节点,则可能需要进行合并操作。合并操作可以将当前节点与兄弟节点合并为一个节点。
-
合并操作可能涉及到移动关键字和指针,同时更新父节点的关键字和指针。
-
重复以上步骤,直到满足平衡条件或达到根节点。
填充策略:
B树中的填充操作的策略通常有以下几种:
-
借用关键字:如果存在关键字数量大于最小关键字数量的兄弟节点,可以选择从兄弟节点中借用一个关键字过来填充当前节点。
-
合并节点:如果没有关键字数量大于最小关键字数量的兄弟节点,可以选择合并当前节点和兄弟节点为一个节点。
B树的默认填充策略通常是优先选择借用关键字的方式进行填充操作。
相关文章:

Mysql--技术文档--B树-数据结构的认知
阿丹解读: B树(B tree)和B树(B-tree)都是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。 基本概念-B树/B树 B树(B-tree)和B树(B tree&#x…...
go gin 自定义验证
我们上一篇已经提到了gin中binding时候可以指定json字段大小等限制,但是那个错误却是英文的,现在想搞成中文的,以便前端可读,demo如下 package mainimport ("net/http""reflect""github.com/gin-gonic/…...
掉了无数头发成地中海后,我整理出了这套40+的大屏模板,快收藏!
最近又有不少粉丝后台问我接不接做可视化大屏,看来可视化大屏是越来越火啦,但老李还是要说一下,老李本身工作就很忙,实在是顾不过来,但老李会在自己体验过后为大家挑选合适的工具和模板,提升大家做大屏的效…...

【从零开始学习JAVA | 第四十六篇】处理请求参数
前言: 在我们之前的学习中,我们已经基本学习完了JAVA的基础内容,从今天开始我们就逐渐进入到JAVA的时间,在这一大篇章,我们将对前后端有一个基本的认识,并要学习如何成为一名合格的后端工程师。今天我们介绍…...
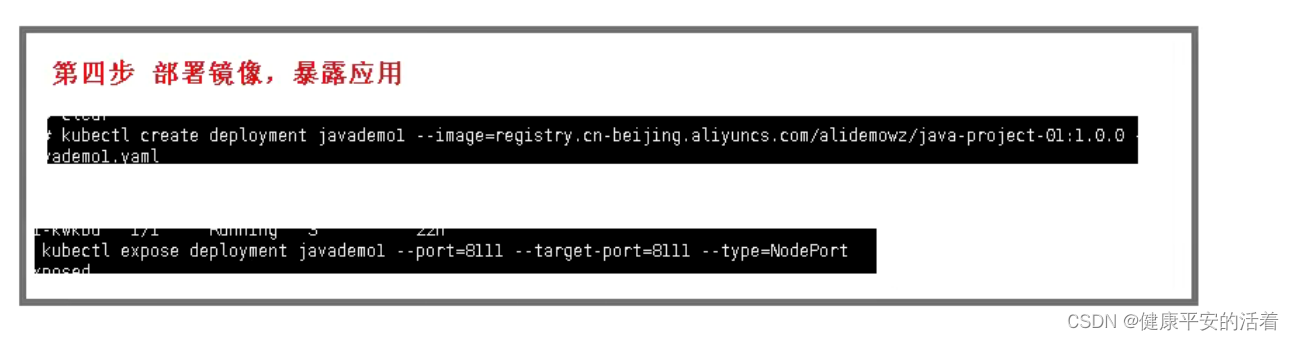
k8s的交付与部署案例操作
一 k8s的概念 1.1 k8s k8s是一个轻量级的,用于管理容器化应用和服务的平台。通过k8s能够进行应用的自动化部署和扩容缩容。 1.2 k8s核心部分 1.prod: 最小的部署单元;一组容器的集合;共享网络;生命周期是短暂的; …...

LVS集群 (四十四)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、集群概述 1. 负载均衡技术类型 2. 负载均衡实现方式 二、LVS结构 三、LVS工作模式 四、LVS负载均衡算法 1. 静态负载均衡 2. 动态负载均衡 五、ipvsadm命令详…...
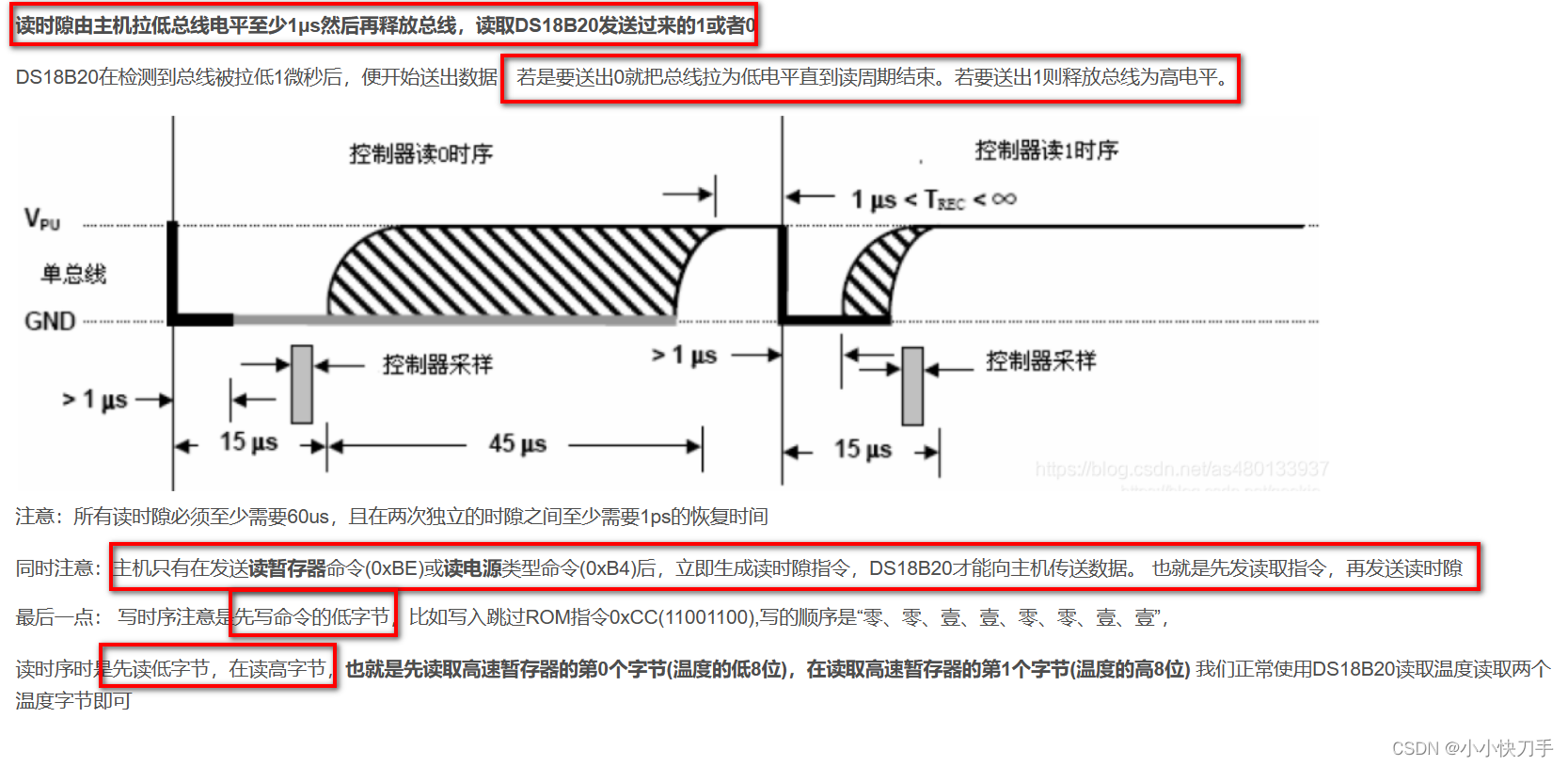
stm32之DS18B20
DS18B20与stm32之间也是通过单总线进行数据的传输的。单总线协议在DHT11中已经介绍过。虽说这两者外设都是单总线,但时序电路却很不一样,DS18B20是更为麻烦一点的。 DS18B20 举例(原码补码反码转换_原码反码补码转换_王小小鸭的博客-CSDN博客…...
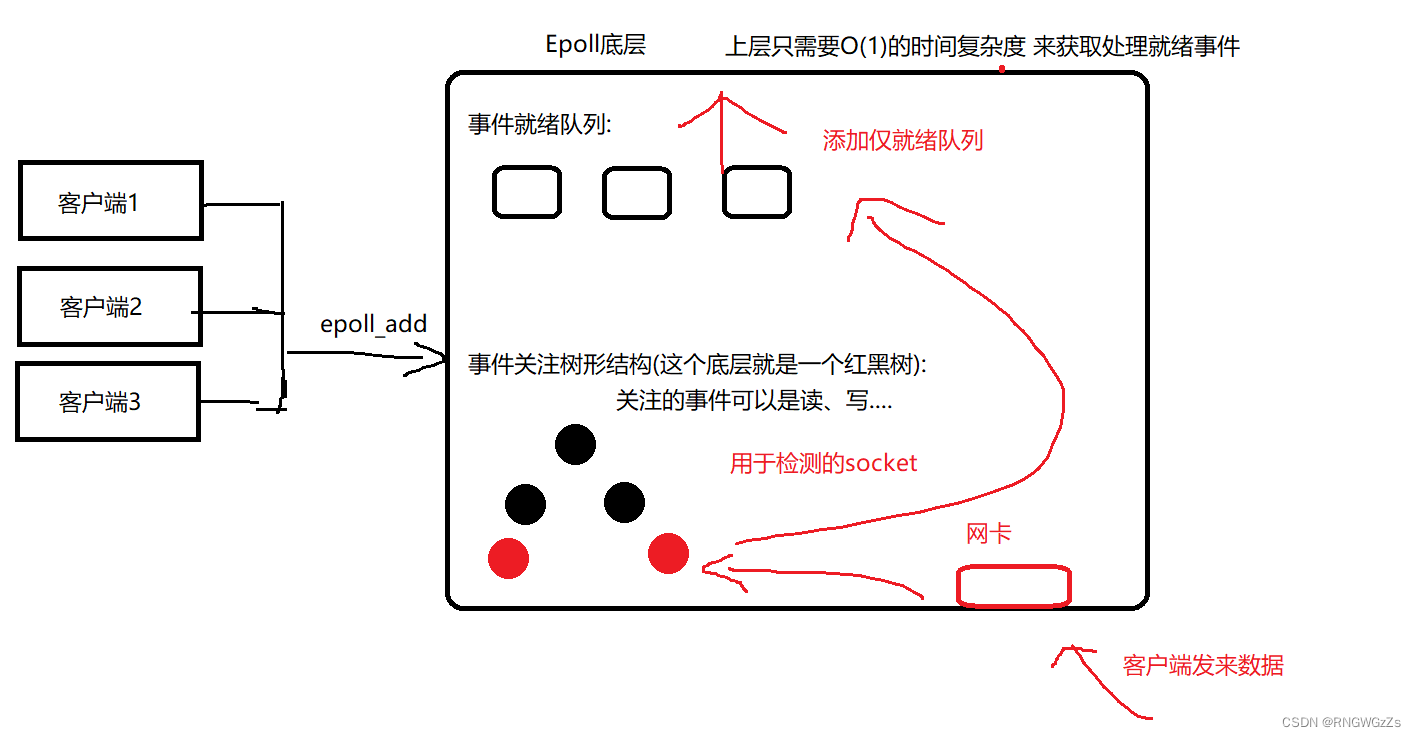
Redis的数据结构与单线程架构
"飞吧,去寻觅红色的流星" Redis中的五种数据结构和编码 Redis是一种通过键值对关系存储数据的软件,在前一篇中,我们可以使用type命令实际返回当前键所对应的数据结构类型,例如: String\list\hash\set等等。 但…...
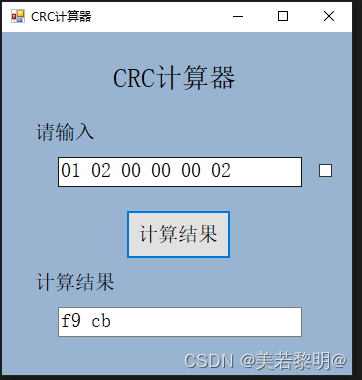
c# modbus CRC计算器(查表法)
一、简介: 本案例为crc计算器,通过查表法计算出结果 1.窗体后台源代码 using Crc; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text…...

2023.08.27 学习周报
文章目录 摘要文献阅读1.题目2.重点3.引言4.方法5.实验结果6.结论 深度学习Majorization-Minimization算法1.基本思想2.要求3.示意图 总结 摘要 This week, I read a computer science on the prediction of atmospheric pollutants in urban environments based on coupled d…...

css元素定位:通过元素的标签或者元素的id、class属性定位,还不明白的伙计,看这个就行了!
前言 大部分人在使用selenium定位元素时,用的是xpath元素定位方式,因为xpath元素定位方式基本能解决定位的需求。xpath元素定位方式更直观,更好理解一些。 css元素定位方式往往被忽略掉了,其实css元素定位方式也有它的价值&…...

基于Spring实现博客项目
访问地址:用户登录 代码获取:基于Spring实现博客项目: Spring项目写博客项目 一.项目开发 1.项目开发阶段 需求评审,需求分析项目设计(接口设计,DB设计等,比较大的需求,需要设计流程图,用例图,UML, model中的字段)开发+自测提测(提交测试…...
数据库第十七课-------ETL任务调度系统的安装和使用
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

Qt 动态中英文切换
背景: 需要界面实现动态国际化,一键点击切换中英文或其他语言。 前提: 已经完成了整个界面的翻译,拿到匹配的ts翻译文件,注意:要保证界面切换后,翻译的全覆盖,要保证任何需要反应的地方,都用到了tr("")包含,不然Linguist会捕捉不到。.ts文件的生成参考下文…...

hdfs操作
hadoop fs [generic options] [-appendToFile … ] [-cat [-ignoreCrc] …] [-checksum …] [-chgrp [-R] GROUP PATH…] [-chmod [-R] <MODE[,MODE]… | OCTALMODE> PATH…] [-chown [-R] [OWNER][:[GROUP]] PATH…] [-copyFromLocal [-f] [-p] [-l] [-d] … ] [-copyTo…...

h5分享页适配手机电脑
实现思路 通过media媒体查询结合rem继承html文字大小来实现。 快捷插件配置 这里使用了VSCode的px to rem插件。 先在插件市场搜索cssrem下载插件; 配置插件 页面编写流程及适配详情 配置meta h5常用配置信息:<meta name"viewport" content&quo…...
崭新商业理念:循环购模式的价值引领-微三云门门
尊敬的创业者们,我是微三云门门,今天我将为您详细探讨一种具有颠覆性的商业模式——循环购模式。这套私域流量裂变策略在实际应用中取得了巨大的成功,某些企业在短短6个月内迅速积累了400万用户! 循环购商业模式的核心聚焦于三个…...
二级MySQL(二)——编程语言,函数
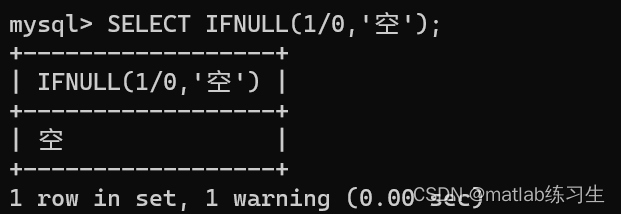
SQL语言又称为【结构化查询语言】 请使用FLOOR(x)函数求小于或等于5.6的最大整数 请使用TRUNCATE(x,y)函数将数字1.98752895保留到小数点后4位 请使用UPPER()函数将字符串‘welcome’转化为大写…...

python爬虫12:实战4
python爬虫12:实战4 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生不好…...
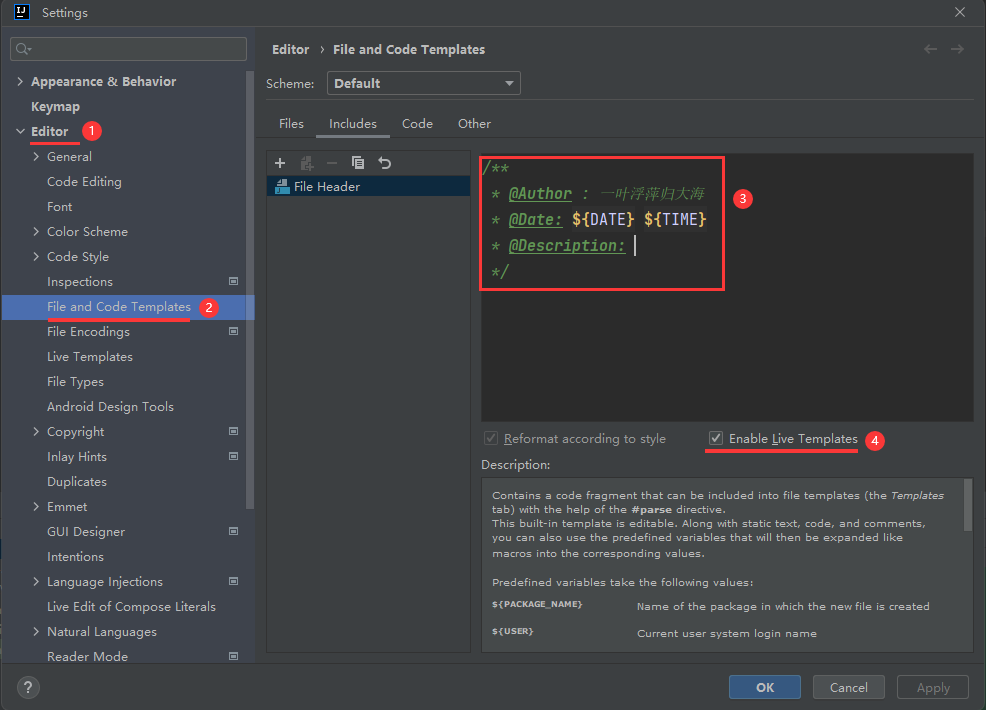
系列十三、idea创建文件自动生成作者信息
File>Settings>Editor>File and Code Templates>Includes>File Header /*** Author : 一叶浮萍归大海* Date: ${DATE} ${TIME}* Description: */...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
