【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(2,常见随机变量及其分布 | 随机变量函数的分布)
文章目录
- 引言
- 三、常见的随机变量及其分布
- 3.1 常见的离散型随机变量及其分布律
- (一)(0-1)分布
- (二)二项分布
- (三)泊松分布
- (四)几何分布
- (五)超几何分布
- 3.2 常见的连续型随机变量及其概率密度
- (一)均匀分布
- (二)指数分布
- (三)正态分布
- 四、随机变量函数的分布
- (一)离散型随机变量函数的分布
- (二)连续型随机变量函数的分布
引言
承接前文,我们继续学习第二章,一维随机变量及其分布的第二部分内容。
三、常见的随机变量及其分布
3.1 常见的离散型随机变量及其分布律
(一)(0-1)分布
设随机变量 X X X 的可能取值为 0 或 1 ,且其概率为 P P P { X = 1 X=1 X=1 } = p , =p, =p, P P P { X = 0 X=0 X=0 } = 1 − p ( 0 < p < 1 =1-p(0 < p < 1 =1−p(0<p<1 ,称 X X X 服从(0-1)分布,记为 X ∼ B ( 1 , p ) . X \sim B(1,p). X∼B(1,p).
(二)二项分布
设随机变量 X X X 的分布律为 P P P { X = k X=k X=k } = C n k p k ( 1 − p ) n − k =C_n^kp^k(1-p)^{n-k} =Cnkpk(1−p)n−k ,其中 k = 0 , 1 , 2 , … , n , 0 < p < 1 , k=0,1,2,\dots,n,0 < p < 1, k=0,1,2,…,n,0<p<1, 称随机变量 X X X 服从二项分布,记为 X ∼ B ( n , p ) . X \sim B(n,p). X∼B(n,p).
回忆一下第一章的伯努利概型,也是二项分布。
(三)泊松分布
设离散型随机变量 X X X 的分布律为 P { X = k } = λ k k ! e − λ , P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda}, P{X=k}=k!λke−λ, 其中, λ > 0 , k = 0 , 1 , 2 , … , n , \lambda > 0,k=0,1,2,\dots,n, λ>0,k=0,1,2,…,n, 称随机变量 X X X 服从参数为 λ \lambda λ 的泊松分布,记为 X ∼ P ( λ ) . X \sim P(\lambda). X∼P(λ).
(四)几何分布
设离散型随机变量 X X X 的分布律为 P { X = k } = p ( 1 − p ) k − 1 , P\{X=k\}=p(1-p)^{k-1}, P{X=k}=p(1−p)k−1, 其中, k = 1 , 2 , … , n , k=1,2,\dots,n, k=1,2,…,n, 称随机变量 X X X 服从几何分布,记为 X ∼ G ( p ) . X \sim G(p). X∼G(p).
服从几何分布的随机变量 X X X 可以这么理解:设伯努利试验中只有两种结果 A , A ‾ , P ( A ) = p A,\overline{A},P(A)=p A,A,P(A)=p ,则 X X X 表示伯努利试验中 A A A 首次发生时的试验次数。
比如, X = 2 X=2 X=2 ,表示试验做了两次才第一次发生,也就是第一次试验没发生,第二次试验发生; X = n X=n X=n ,表示前 n − 1 n-1 n−1 次试验没发生,第 n n n 次试验发生。这样就好理解了,公式也一下就记得住。
(五)超几何分布
设离散型随机变量 X X X 的分布律为 P { X = k } = C M k ⋅ C N − M n − k C N n , P\{X=k\}=\frac{C_M^k \cdot C_{N-M}^{n-k}}{C_N^n}, P{X=k}=CNnCMk⋅CN−Mn−k, 其中, M , N , k , n M,N,k,n M,N,k,n 为自然数,且 M ≤ N , m a x { N − M , 0 } ≤ k ≤ m i n { M , n } , n ≤ N M \leq N,max\{N-M,0\} \leq k \leq min\{M,n\},n \leq N M≤N,max{N−M,0}≤k≤min{M,n},n≤N , 称随机变量 X X X 服从超几何分布,记为 X ∼ H ( n , M , N ) . X \sim H(n,M,N). X∼H(n,M,N).
3.2 常见的连续型随机变量及其概率密度
(一)均匀分布
设随机变量 X X X 的概率密度为 f ( x ) = { 1 b − a , a ≤ x ≤ b 0 , e l s e , f(x) = \begin{cases} \frac{1}{b-a}, & a \leq x \leq b \\ 0, & else \\ \end{cases}, f(x)={b−a1,0,a≤x≤belse, 称随机变量 X X X 在区间 ( a , b ) (a,b) (a,b) 内服从均匀分布,记为 X ∼ U ( a , b ) . X \sim U(a,b). X∼U(a,b).
若随机变量 X ∼ U ( a , b ) X \sim U(a,b) X∼U(a,b),则其分布函数为 F ( x ) = { 0 , x < a x − a b − a , a ≤ x ≤ b 1 , x ≥ b F(x)=\begin{cases} 0, & x < a \\ \frac{x-a}{b-a}, & a \leq x \leq b \\ 1,& x \geq b\\ \end{cases} F(x)=⎩ ⎨ ⎧0,b−ax−a,1,x<aa≤x≤bx≥b
(二)指数分布
设随机变量 X X X 的概率密度为 f ( x ) = { λ e − λ x x > 0 0 , x ≤ 0 ( λ > 0 ) f(x) = \begin{cases} \lambda e^{-\lambda x} & x > 0 \\ 0, & x \leq 0 \\ \end{cases}(\lambda > 0) f(x)={λe−λx0,x>0x≤0(λ>0) 称随机变量 X X X 服从参数为 λ \lambda λ 的指数分布,记为 X ∼ E ( λ ) . X \sim E(\lambda). X∼E(λ).
若随机变量 X ∼ E ( λ ) X \sim E(\lambda) X∼E(λ),则其分布函数为 F ( x ) = { 1 − e − λ x , x ≥ 0 0 , x < 0 F(x)=\begin{cases} 1-e^{-\lambda x}, & x \geq 0 \\ 0,& x < 0\\ \end{cases} F(x)={1−e−λx,0,x≥0x<0
(三)正态分布
设随机变量 X X X 的概率密度为 f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 ( − ∞ < x < + ∞ ) , f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}(-\infty < x < +\infty), f(x)=2πσ1e−2σ2(x−μ)2(−∞<x<+∞), 称随机变量 X X X 服从正态分布,记为 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X∼N(μ,σ2),其概率密度函数如下图所示:

特别地,若 μ = 0 , σ = 1 \mu =0,\sigma=1 μ=0,σ=1 ,称随机变量 X X X 服从标准正态分布,记为 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1) ,其概率密度为 φ ( x ) = 1 2 π e − x 2 2 ( − ∞ < x < + ∞ ) , \varphi(x)= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}(-\infty < x < +\infty), φ(x)=2π1e−2x2(−∞<x<+∞), 其概率密度函数如下图所示:

分布函数为 Φ ( x ) = ∫ − ∞ x φ ( t ) d t . \varPhi(x)=\int_{-\infty}^x\varphi(t)dt. Φ(x)=∫−∞xφ(t)dt. 正态分布具有如下性质:
(1)若 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1) ,则其概率密度函数 φ ( x ) \varphi(x) φ(x) 为偶函数,且 P { X ≤ 0 } = Φ ( 0 ) = 0.5 , P\{X \leq 0 \}=\varPhi(0)=0.5, P{X≤0}=Φ(0)=0.5, P { X ≤ − a } = Φ ( − a ) = P { X > a } = 1 − Φ ( a ) . P\{X \leq-a\}=\varPhi(-a)=P\{X > a\}=1-\varPhi(a). P{X≤−a}=Φ(−a)=P{X>a}=1−Φ(a). (2)若随机变量 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X∼N(μ,σ2) ,则 P { X ≤ μ } = P { X > μ } = 0.5 , P\{X \leq \mu\}=P\{X > \mu\}=0.5, P{X≤μ}=P{X>μ}=0.5, 即正态分布的密度函数的图像关于 x = μ x=\mu x=μ 对称。
(3)若随机变量 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X∼N(μ,σ2) ,则 X − μ σ ∼ N ( 0 , 1 ) . \frac{X-\mu}{\sigma} \sim N(0,1). σX−μ∼N(0,1).
(4)若随机变量 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^2) X∼N(μ,σ2) ,则 P { a < X ≤ b } = F ( b ) − F ( a ) = Φ ( b − μ σ ) − Φ ( a − μ σ ) . P\{a < X \leq b\}=F(b)-F(a)=\varPhi(\frac{b-\mu}{\sigma})-\varPhi(\frac{a-\mu}{\sigma}). P{a<X≤b}=F(b)−F(a)=Φ(σb−μ)−Φ(σa−μ). (5) Φ ( a ) + Φ ( b ) = { < 1 , a + b < 0 = 1 , a + b = 0 > 1 , a + b > 0 \varPhi(a)+\varPhi(b)=\begin{cases} <1, & a+b< 0 \\ =1,& a+b= 0\\ \ >1 ,& a+b> 0\\ \end{cases} Φ(a)+Φ(b)=⎩ ⎨ ⎧<1,=1, >1,a+b<0a+b=0a+b>0
四、随机变量函数的分布
设 X X X 为随机变量,其分布已知,称 Y = φ ( X ) Y=\varphi(X) Y=φ(X) 为随机变量 X X X 的函数,研究随机变量 Y Y Y 的分布及随机变量函数的分布。
(一)离散型随机变量函数的分布
设 X X X 为随机变量, Y = φ ( X ) Y=\varphi(X) Y=φ(X) ,只要根据 X X X 的可能取值及概率求出 Y Y Y 的可能取值及概率,即可得到 Y Y Y 的分布律。
(二)连续型随机变量函数的分布
设 X X X 为连续型随机变量,其概率密度为 f ( x ) f(x) f(x) ,又 Y = φ ( x ) Y=\varphi(x) Y=φ(x) ,求随机变量 Y Y Y 的分布时,先求 Y Y Y 的分布函数 P { Y ≤ y } = P { φ ( X ) ≤ y } , P\{Y \leq y\}=P\{\varphi(X) \leq y\}, P{Y≤y}=P{φ(X)≤y}, 再通过 X X X 的分布求出 Y Y Y 的分布。
相关文章:

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(2,常见随机变量及其分布 | 随机变量函数的分布)
文章目录 引言三、常见的随机变量及其分布3.1 常见的离散型随机变量及其分布律(一)(0-1)分布(二)二项分布(三)泊松分布(四)几何分布(五࿰…...
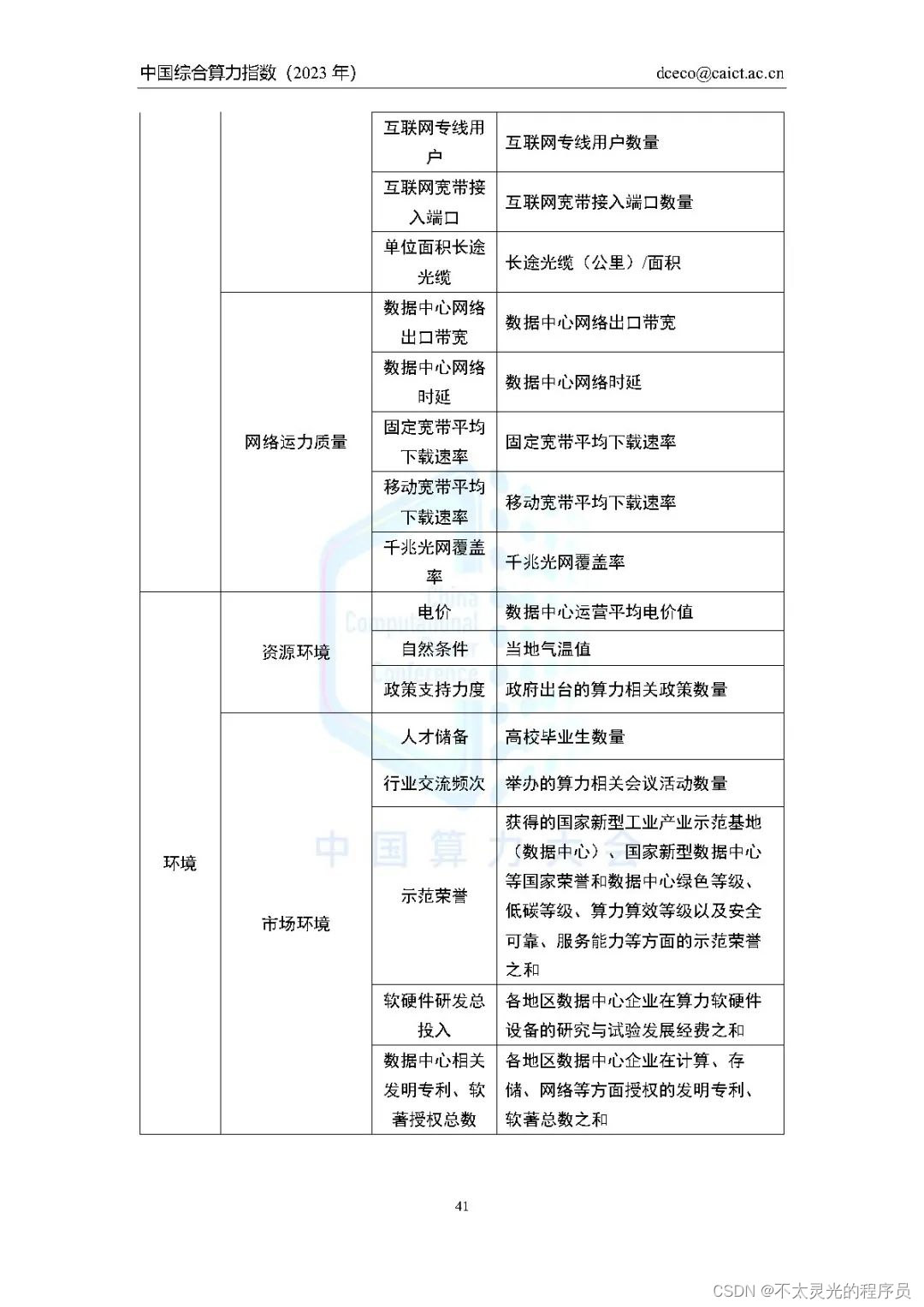
【2023中国算力大会】《中国综合算力指数(2023年)》出炉,宁夏“资源环境”位列全国第1,“算力”跃入Top10
2023年8月18日-19日,2023中国算力大会在宁夏银川举行,本届大会以“算领新产业潮流 力赋高质量发展”为主题,打造“主题论坛、成果展示、产业推介、先锋引领”四大核心内容,全面展示算力产业发展最新成果,为产业各方搭建…...

自动设置服务器全教程
亲爱的爬虫探险家!在网络爬虫的世界里,自动设置代理服务器是一个非常有用的技巧。今天,作为一家代理服务器供应商,我将为你呈上一份轻松实用的教程,帮助你轻松搞定爬虫自动设置代理服务器。 一、为什么需要自动设置代…...
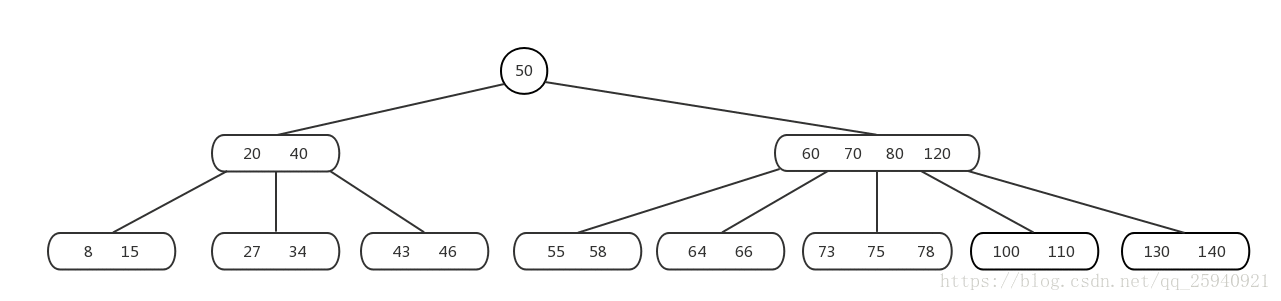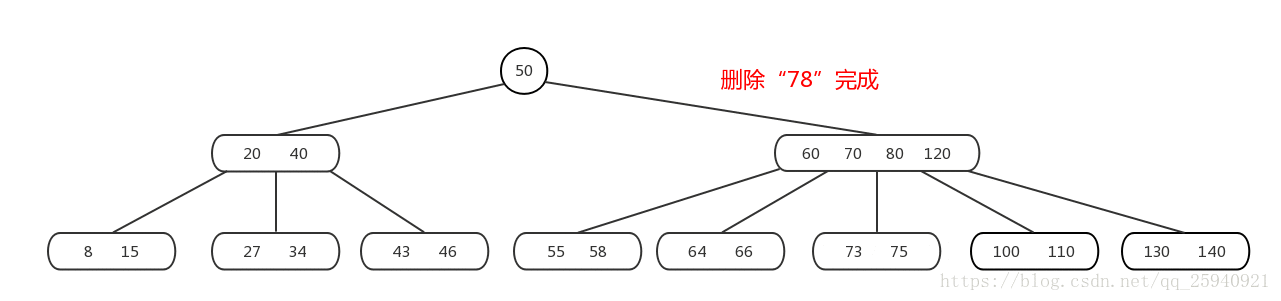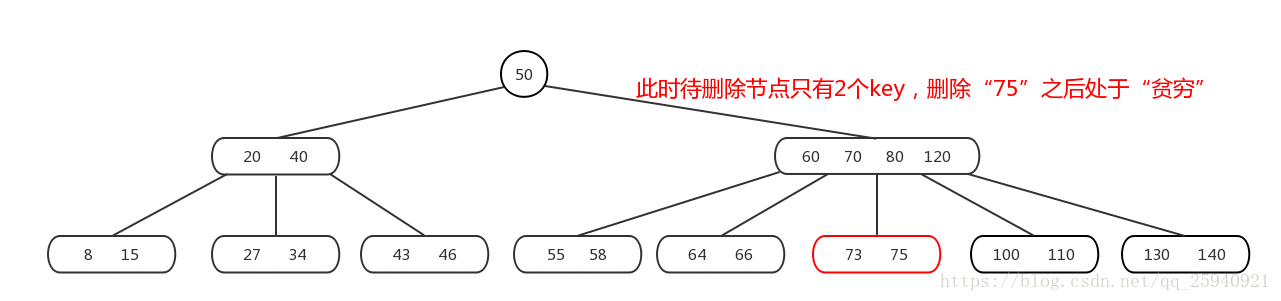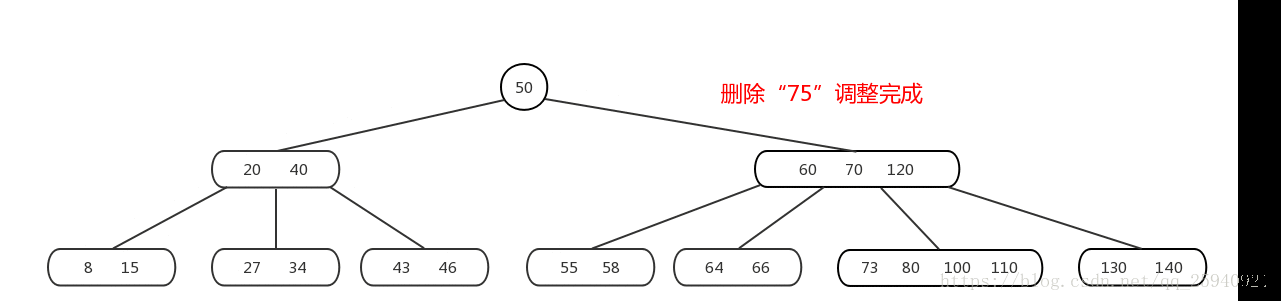
Mysql--技术文档--B树-数据结构的认知
阿丹解读: B树(B tree)和B树(B-tree)都是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。 基本概念-B树/B树 B树(B-tree)和B树(B tree&#x…...
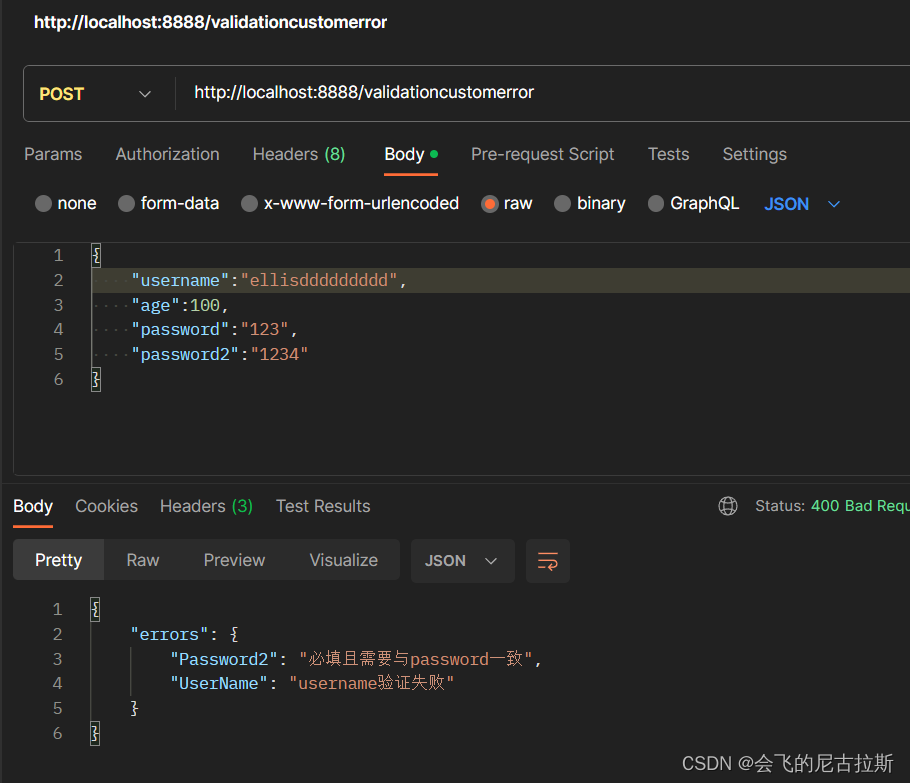
go gin 自定义验证
我们上一篇已经提到了gin中binding时候可以指定json字段大小等限制,但是那个错误却是英文的,现在想搞成中文的,以便前端可读,demo如下 package mainimport ("net/http""reflect""github.com/gin-gonic/…...
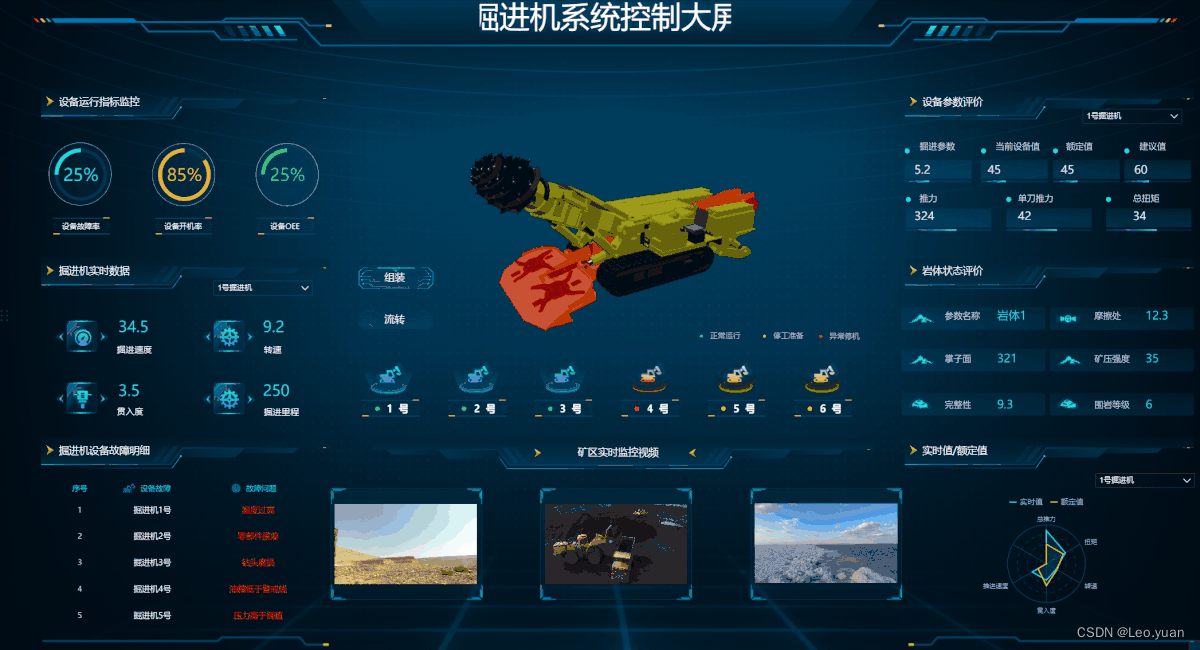
掉了无数头发成地中海后,我整理出了这套40+的大屏模板,快收藏!
最近又有不少粉丝后台问我接不接做可视化大屏,看来可视化大屏是越来越火啦,但老李还是要说一下,老李本身工作就很忙,实在是顾不过来,但老李会在自己体验过后为大家挑选合适的工具和模板,提升大家做大屏的效…...

【从零开始学习JAVA | 第四十六篇】处理请求参数
前言: 在我们之前的学习中,我们已经基本学习完了JAVA的基础内容,从今天开始我们就逐渐进入到JAVA的时间,在这一大篇章,我们将对前后端有一个基本的认识,并要学习如何成为一名合格的后端工程师。今天我们介绍…...
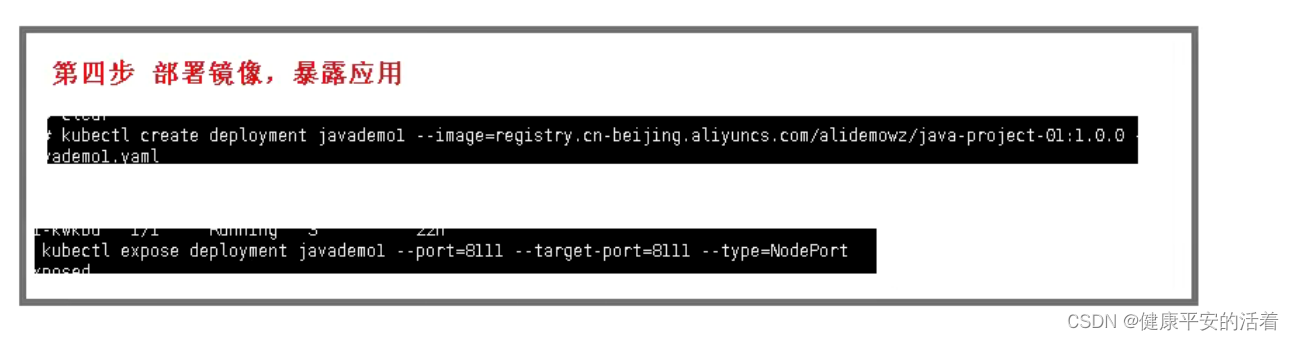
k8s的交付与部署案例操作
一 k8s的概念 1.1 k8s k8s是一个轻量级的,用于管理容器化应用和服务的平台。通过k8s能够进行应用的自动化部署和扩容缩容。 1.2 k8s核心部分 1.prod: 最小的部署单元;一组容器的集合;共享网络;生命周期是短暂的; …...

LVS集群 (四十四)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、集群概述 1. 负载均衡技术类型 2. 负载均衡实现方式 二、LVS结构 三、LVS工作模式 四、LVS负载均衡算法 1. 静态负载均衡 2. 动态负载均衡 五、ipvsadm命令详…...
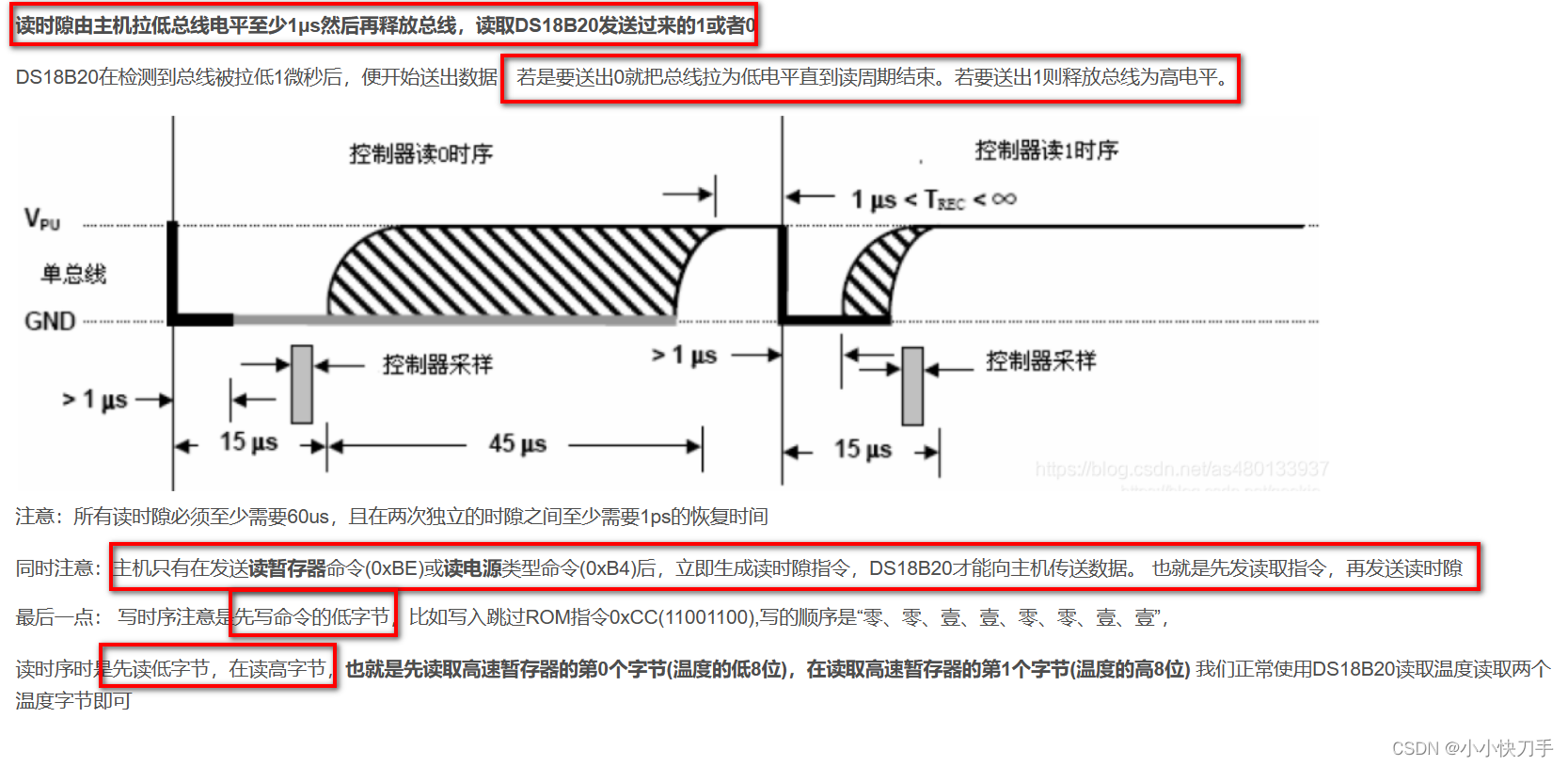
stm32之DS18B20
DS18B20与stm32之间也是通过单总线进行数据的传输的。单总线协议在DHT11中已经介绍过。虽说这两者外设都是单总线,但时序电路却很不一样,DS18B20是更为麻烦一点的。 DS18B20 举例(原码补码反码转换_原码反码补码转换_王小小鸭的博客-CSDN博客…...
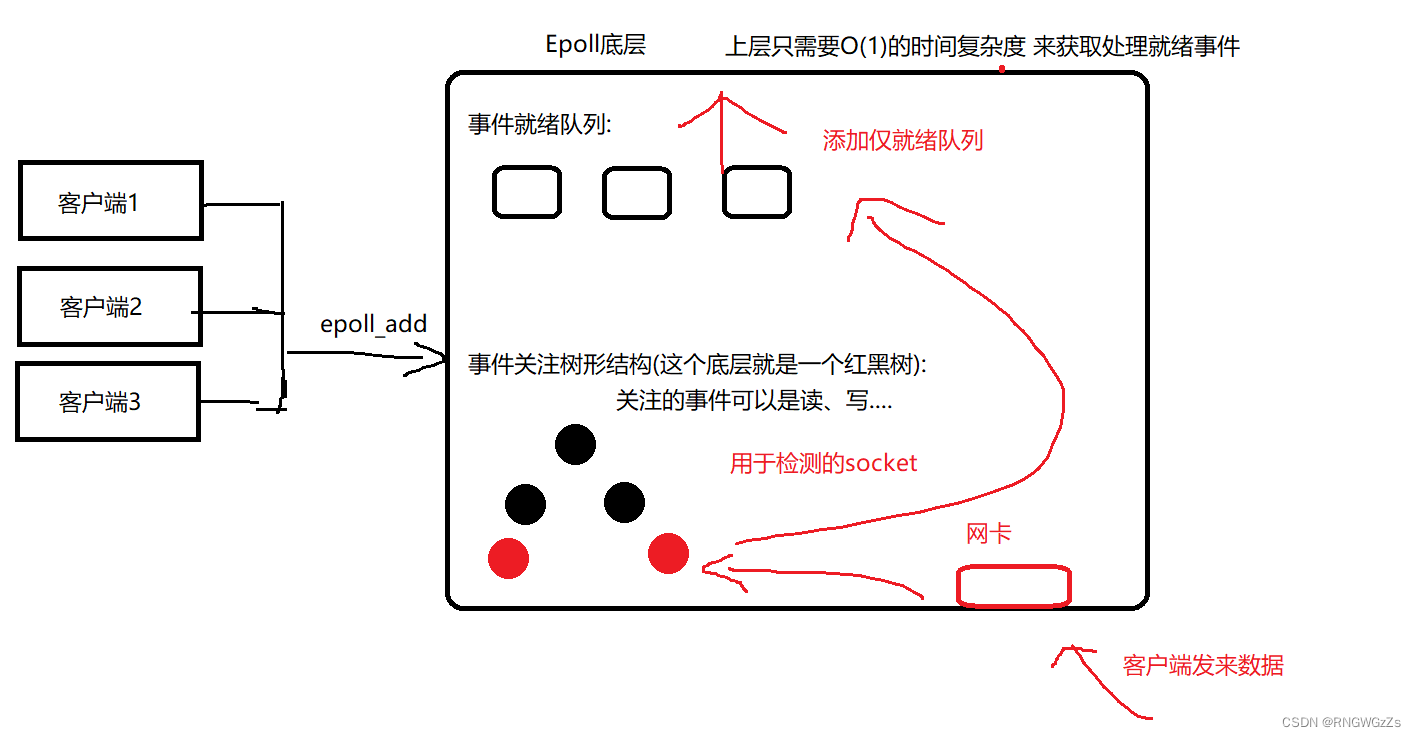
Redis的数据结构与单线程架构
"飞吧,去寻觅红色的流星" Redis中的五种数据结构和编码 Redis是一种通过键值对关系存储数据的软件,在前一篇中,我们可以使用type命令实际返回当前键所对应的数据结构类型,例如: String\list\hash\set等等。 但…...
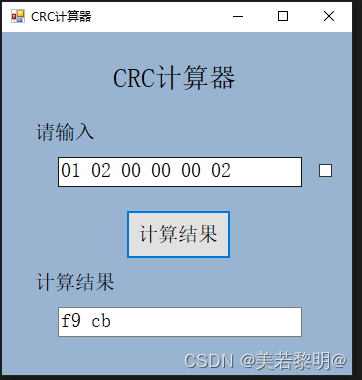
c# modbus CRC计算器(查表法)
一、简介: 本案例为crc计算器,通过查表法计算出结果 1.窗体后台源代码 using Crc; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text…...

2023.08.27 学习周报
文章目录 摘要文献阅读1.题目2.重点3.引言4.方法5.实验结果6.结论 深度学习Majorization-Minimization算法1.基本思想2.要求3.示意图 总结 摘要 This week, I read a computer science on the prediction of atmospheric pollutants in urban environments based on coupled d…...

css元素定位:通过元素的标签或者元素的id、class属性定位,还不明白的伙计,看这个就行了!
前言 大部分人在使用selenium定位元素时,用的是xpath元素定位方式,因为xpath元素定位方式基本能解决定位的需求。xpath元素定位方式更直观,更好理解一些。 css元素定位方式往往被忽略掉了,其实css元素定位方式也有它的价值&…...

基于Spring实现博客项目
访问地址:用户登录 代码获取:基于Spring实现博客项目: Spring项目写博客项目 一.项目开发 1.项目开发阶段 需求评审,需求分析项目设计(接口设计,DB设计等,比较大的需求,需要设计流程图,用例图,UML, model中的字段)开发+自测提测(提交测试…...
数据库第十七课-------ETL任务调度系统的安装和使用
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

Qt 动态中英文切换
背景: 需要界面实现动态国际化,一键点击切换中英文或其他语言。 前提: 已经完成了整个界面的翻译,拿到匹配的ts翻译文件,注意:要保证界面切换后,翻译的全覆盖,要保证任何需要反应的地方,都用到了tr("")包含,不然Linguist会捕捉不到。.ts文件的生成参考下文…...

hdfs操作
hadoop fs [generic options] [-appendToFile … ] [-cat [-ignoreCrc] …] [-checksum …] [-chgrp [-R] GROUP PATH…] [-chmod [-R] <MODE[,MODE]… | OCTALMODE> PATH…] [-chown [-R] [OWNER][:[GROUP]] PATH…] [-copyFromLocal [-f] [-p] [-l] [-d] … ] [-copyTo…...

h5分享页适配手机电脑
实现思路 通过media媒体查询结合rem继承html文字大小来实现。 快捷插件配置 这里使用了VSCode的px to rem插件。 先在插件市场搜索cssrem下载插件; 配置插件 页面编写流程及适配详情 配置meta h5常用配置信息:<meta name"viewport" content&quo…...
崭新商业理念:循环购模式的价值引领-微三云门门
尊敬的创业者们,我是微三云门门,今天我将为您详细探讨一种具有颠覆性的商业模式——循环购模式。这套私域流量裂变策略在实际应用中取得了巨大的成功,某些企业在短短6个月内迅速积累了400万用户! 循环购商业模式的核心聚焦于三个…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
