专题:平面、空间直线参数方程下的切线斜率问题
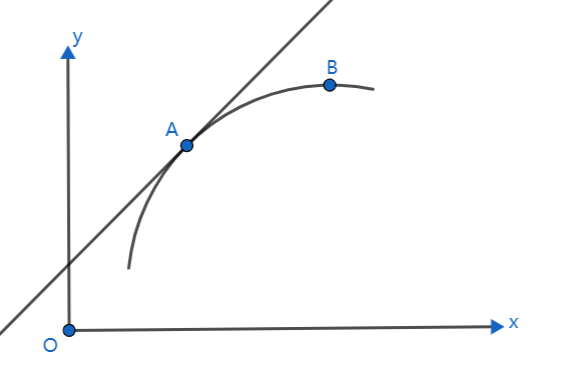
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。
如上图所示。 设 y = f ( x ) , x = φ ( t ) , y = ψ ( t ) 当 t = t 0 时, x = x 0 , y = y 0 ,即点 A 坐标为 ( x 0 , y 0 ) 点 A 处的导数 f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) φ ( t 0 + Δ t ) − φ ( t 0 ) = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = lim Δ t → 0 ψ ( t 0 + Δ t ) − ψ ( t 0 ) Δ t / lim Δ t → 0 φ ( t 0 + Δ t ) − φ ( t 0 ) Δ t = ψ ′ ( t 0 ) φ ′ ( t 0 ) 因此点 A 处的切线向量可表示为 ( ψ ′ ( t 0 ) , φ ′ ( t 0 ) ) 而切线方程为 y − y 0 = ψ ′ ( t 0 ) φ ′ ( t 0 ) ( x − x 0 ) ,即 y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) 同理可得空间直线的点向式方程为: y − y 0 ψ ′ ( t 0 ) = x − x 0 φ ′ ( t 0 ) = z − z 0 ω ′ ( t 0 ) 如上图所示。\\ 设y=f(x),x=\varphi(t),y=\psi(t) \\ 当t=t_0时,x=x_0,y=y_0,即点A坐标为(x_0,y_0) \\ 点A处的导数f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\varphi(t_0+\Delta t)-\varphi(t_0)} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\lim_{\Delta t \to 0}\frac{\psi(t_0+\Delta t)-\psi(t_0)}{\Delta t}/\lim_{\Delta t \to 0}\frac{\varphi(t_0+\Delta t)-\varphi(t_0)}{\Delta t} \\ \,\\ =\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)} \\ \,\\ 因此点A处的切线向量可表示为(\psi^\prime(t_0),\varphi^\prime(t_0)) \\ 而切线方程为y-y_0=\frac{\psi^\prime(t_0)}{\varphi^\prime(t_0)}(x-x_0),即\frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)} \\ \,\\ 同理可得空间直线的点向式方程为:\\ \frac{y-y_0}{\psi^\prime(t_0)}=\frac{x-x_0}{\varphi^\prime(t_0)}=\frac{z-z_0}{\omega^\prime(t_0)} 如上图所示。设y=f(x),x=φ(t),y=ψ(t)当t=t0时,x=x0,y=y0,即点A坐标为(x0,y0)点A处的导数f′(x0)=Δx→0limΔxΔy=Δt→0limφ(t0+Δt)−φ(t0)ψ(t0+Δt)−ψ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δtφ(t0+Δt)−φ(t0)=Δt→0limΔtψ(t0+Δt)−ψ(t0)/Δt→0limΔtφ(t0+Δt)−φ(t0)=φ′(t0)ψ′(t0)因此点A处的切线向量可表示为(ψ′(t0),φ′(t0))而切线方程为y−y0=φ′(t0)ψ′(t0)(x−x0),即ψ′(t0)y−y0=φ′(t0)x−x0同理可得空间直线的点向式方程为:ψ′(t0)y−y0=φ′(t0)x−x0=ω′(t0)z−z0
相关文章:

专题:平面、空间直线参数方程下的切线斜率问题
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。 如上图所示。 设 y f ( x ) , x φ ( t ) , y ψ ( t ) 当 t t 0 时, x x 0 , y y 0 ,即点 A 坐…...
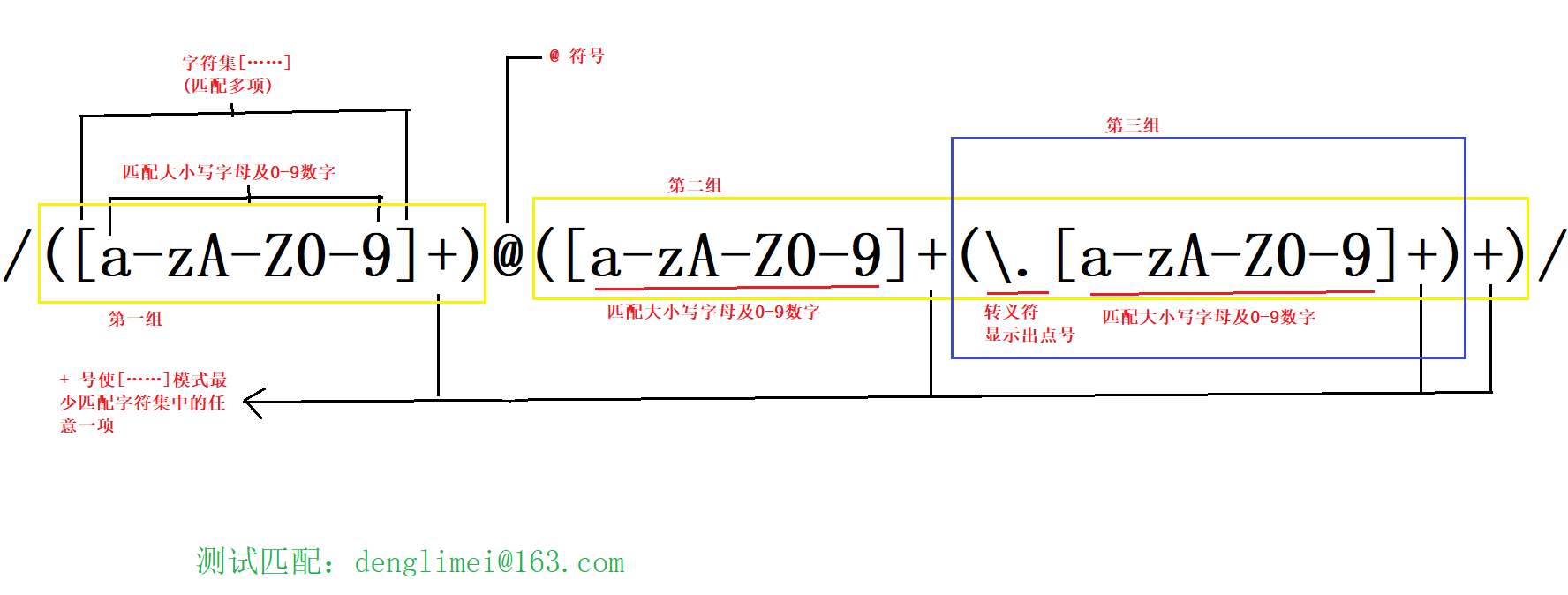
JavaScript—对象与构造方法
目录 json对象(字面值) js中对象是什么? 如何使用? 关联数组 js对象和C#对象有什么区别? 构造函数 什么是构造方法? 如何使用构造方法? 如何添加成员? 对象的动态成员 正则…...

微信小程序社区户口管理的系统设计与实现
摘要 我国的户口管理制度由来已久,我国对于合法居民在新生儿的出生、户口的落地、迁移以及户口的注销上都有着详细的管理条例进行约束。通过户口的管理可以更好地对我国的居民人数进行有效的内容统计,在进行人口普查的过程中也能够实现更好的、更加精准的…...
闲人闲谈PS之四十六——网络生产全流程
惯例闲话:下半年已开始块行情似乎又是一波大涨,很多朋友委托我介绍PS顾问,很多朋友已经上了能源系统项目,这就造成装备制造的PS又是极度紧缺,rate也还可以,搞的自己也有点心痒痒。这种逆势大涨,…...
如何在VR头显端实现低延迟的RTSP或RTMP播放
技术背景 VR(虚拟现实技术)给我们带来身临其境的视觉体验,广泛的应用于城市规划、教育培训、工业仿真、房地产、水利电力、室内设计、文旅、军事等众多领域,常用的行业比如: 教育行业:VR头显可以用于教育…...
【工具类】提高办公效率(兼具有趣、好玩)
1 Wormhole 免费免注册登录在线、不限速文件传输 Simple, private file sharing https://wormhole.app/ 2 ALL to ALL 在线格式转换 免费、免注册登录 国内最全类型的在线文件转换平台,免费、快速,无须下载安装任何软件。 https://www.alltoall.net/ …...
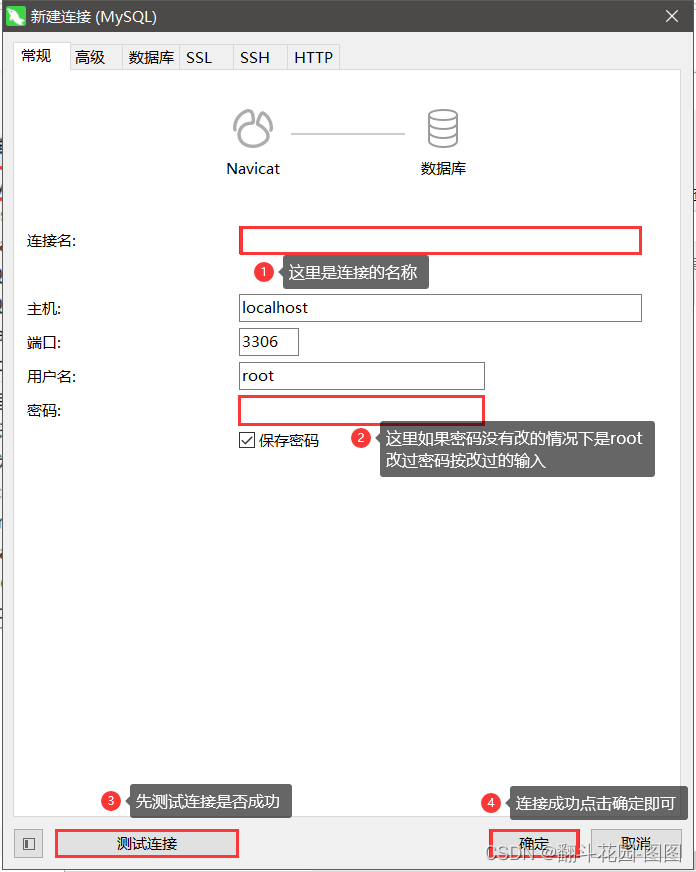
navicat连接数据库的方法(易懂)
1.首页要先下载Navicat 官网下载即可 2.下载完点击进入 找到左上角的连接 3.点击选择MySQL... 4.点击进入开始连接数据库...
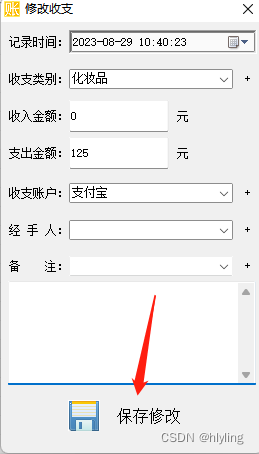
收支明细管理实操:如何准确记录并修改收支明细?
宣传软文: 在日常生活中,收支明细的管理至关重要,无论是个人还是企业。准确的记录不仅能有效管理财务,还能提供清晰的依据以供分析和决策。但在实际操作中,可能出现记录错误的情况。本文将详细介绍如何记录和修改收支明…...

SSL证书的工作原理是怎样的?
传统的网络通信采用的是HTTP传输协议,数据全程公开暴露,很容易被第三方监听和窃取,对用户和网站的数据安全造成很大威胁。为了保护用户的数据安全,SSL证书逐渐普及并应用于政府和企业网站之中,成为了提升数据安全水平&…...
)
Java发送请求到第三方(RestTemplate方法)
Get请求 try {RestTemplate restTemplate = new RestTemplate();//设置请求头HttpHeaders headers = new HttpHeaders();headers.add("Authorization", "Bearer token");headers.add("User-Agent", "Mozilla/5.0");HttpEntity entity…...
CentOS 7 Nacos 设置开机自动重启
一、说明 Nacos如果是手动启动的话,在服务器宕机或者重启后,没有自动运行,影响很多业务系统,需要每次手动执行命令 startup.sh -m standalone,才能启动 Nacos 服务,不能像docker服务一样,使用 …...
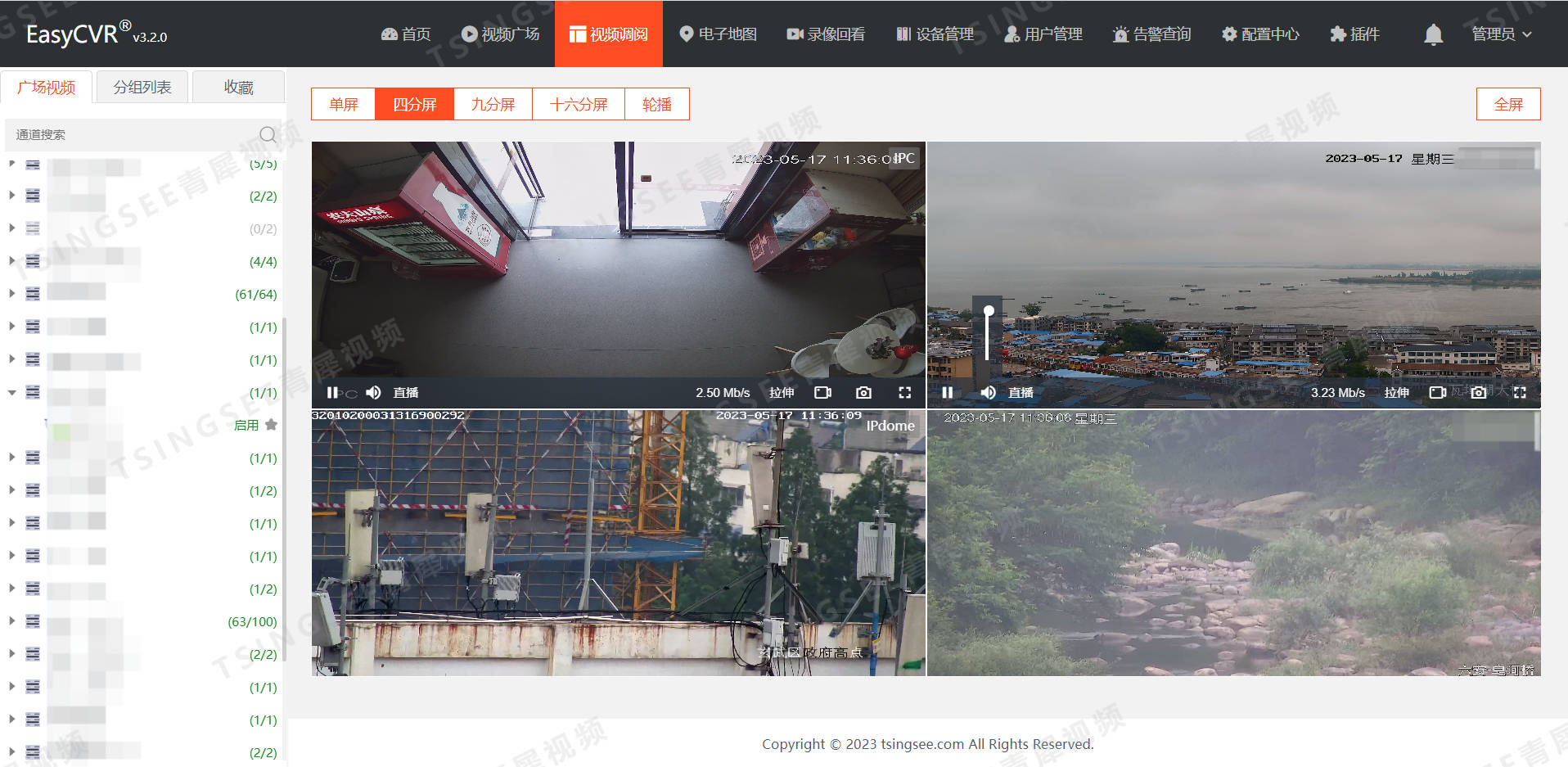
安防监控平台EasyCVR视频汇聚平台增加首页告警类型的详细介绍
安防监控/视频集中存储/云存储EasyCVR视频汇聚平台,可支持海量视频的轻量化接入与汇聚管理。平台能提供视频存储磁盘阵列、视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、平台级联、H.265自动转码等…...

构建安全可信、稳定可靠的RISC-V安全体系
安全之安全(security)博客目录导读 2023 RISC-V中国峰会 安全相关议题汇总 说明:本文参考RISC-V 2023中国峰会如下议题,版权归原作者所有。...
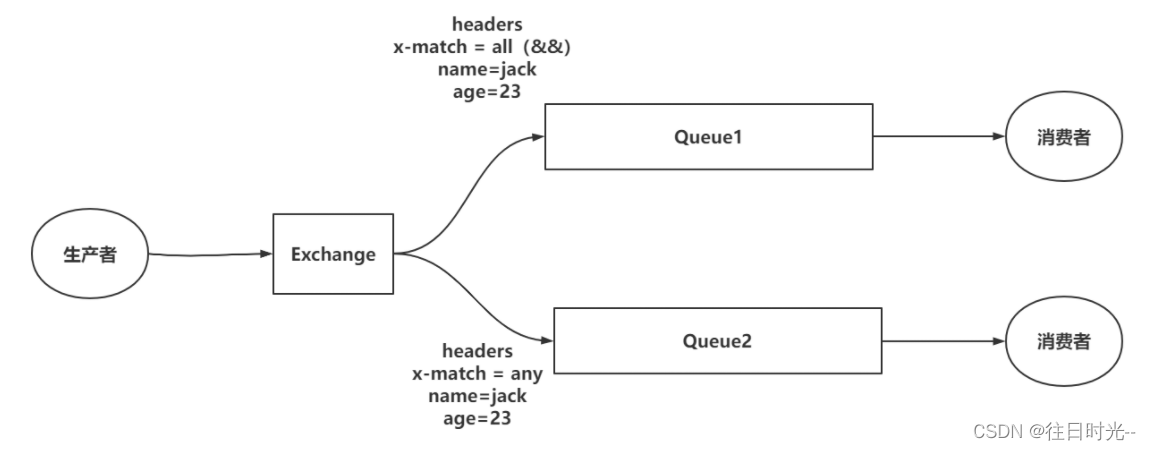
3.RabbitMQ 架构以及 通信方式
一、RabbitMQ的架构 RabbitMQ的架构可以查看官方地址 可以看出RabbitMQ中主要分为三个角色: Publisher:消息的发布者,将消息发布到RabbitMQ中的ExchangeRabbitMQ服务:Exchange接收Publisher的消息,并且根据Routes策…...
分布式事务篇-2.1 阿里云轻量服务器--Docker--部署Seata
文章目录 前言一、Seata 介绍二、Docker 部署:2.1.拉取镜像:2.2.运行镜像:2.3.拷贝配置文件:2.4.部署:2.5.参数解释:2.5.1 端口:2.5.2 SEATA_IP:2.5.3 SEATA_PORT:2.5.4 …...
C语言这么没用??
今日话题,C语言真的这么不堪吗?最近我兄弟向我倾诉,他在几天前受到老板的责骂,原因是他只懂C语言编程,无法达到老板的期望。其实不是C语言不堪,而是嵌入式领域复杂性多种多样,需要灵活的解决方案…...

Docker运维篇
Docker运维篇 Docker 设置自启Docker 指定容器设置自启重启linux 计算机网络常见错误汇总centos 7 Docker容器启动报WARNING: IPv4 forwarding is disabled. Networking will not work Docker 设置自启 # 重启docker sudo systemctl enable docker# 设置开机自启 systemctl e…...

【数学建模】清风数模正课7 多元线性回归模型
多元线性回归分析 回归分析就是,通过研究自变量X和因变量Y的相关关系,来解释Y的形成机制,从而达到通过X去预测Y的目的。 所以回归分析需要完成三个使命,首先是识别重要变量,其次是判断正负相关,最后是估计…...

文心一言 VS 讯飞星火 VS chatgpt (83)-- 算法导论8.1 4题
四、用go语言,假设现有一个包含n个元素的待排序序列。该序列由 n/k 个子序列组成,每个子序列包含k个元素。一个给定子序列中的每个元素都小于其后继子序列中的所有元素,且大于其前驱子序列中的每个元素。因此,对于这个长度为 n 的…...
温故知新之:代理模式,静态代理和动态代理(JDK动态代理)
0、前言 代理模式可以在不修改被代理对象的基础上,通过扩展代理类,进行一些功能的附加与增强。 1、静态代理 静态代理是一种代理模式的实现方式,它在编译期间就已经确定了代理对象,需要为每一个被代理对象创建一个代理类。静态代…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
