B - 负环
题目描述
给定一个 n 个点的有向图,请求出图中是否存在从顶点 11 出发能到达的负环。
负环的定义是:一条边权之和为负数的回路。
输入格式
本题单测试点有多组测试数据。
输入的第一行是一个整数 T,表示测试数据的组数。对于每组数据的格式如下:
第一行有两个整数,分别表示图的点数 n 和接下来给出边信息的条数 m。
接下来 m 行,每行三个整数 u,v,w。
- 若 w≥0,则表示存在一条从 u 至 v 边权为 w 的边,还存在一条从 v 至 u 边权为 w 的边。
- 若 w<0,则只表示存在一条从 u 至 v 边权为 w 的边。
输出格式
对于每组数据,输出一行一个字符串,若所求负环存在,则输出 YES,否则输出 NO。
输入输出样例
输入 #1复制
2 3 4 1 2 2 1 3 4 2 3 1 3 1 -3 3 3 1 2 3 2 3 4 3 1 -8
输出 #1复制
NO YES
说明/提示
数据规模与约定
对于全部的测试点,保证:
- 1≤n≤2×10^3,1≤m≤3×10^3。
- 1≤u,v≤n,−10^4≤w≤10^4。
- 1≤T≤10。
提示
请注意,m 不是图的边数。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1000010;
const int INF = 0x3f3f3f3f;int n, m;
int h[N], w[N], ne[N], e[N], idx;
/*
用邻接表存储图的信息:
h[N]存储所有的表头
e[N]存储所有的边,表示边的终点
w[N]表示边的权重
ne[N]存储每个节点下一个值为多少
idx表示坐标
*/
int dist[N], cnt[N];
//dist[N]表示到某点的最短距离
//cnt[N]表示到某点的组成最短距离所用到的边数bool st[N];
//用于标记当前的点是否在队列中//加入边
void add(int a, int b, int c)
{e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++;
}bool spfa()
{//初始化memset(dist, INF, sizeof dist);memset(st, false, sizeof st);memset(cnt, 0, sizeof cnt);//根据题目所得出的操作:从顶点1出发所能到达的负环queue<int> q;dist[1] = 0;q.push(1);st[1] = true;//直到队内没有元素为止while (q.size()){int temp = q.front(); //取出队首元素q.pop();st[temp] = false;for (int i = h[temp]; i != -1; i = ne[i]){int j = e[i]; //当前边的终点if (dist[j] > dist[temp] + w[i]) // 如果通过当前节点可以松弛到终点j{dist[j] = dist[temp] + w[i];cnt[j] = cnt[temp] + 1;if (cnt[j] >= n) return true; //若边数为n,则证明有n+1个点,这就是一个负环if (!st[j]){q.push(j); // 将更新的节点加入队列st[j] = true;}}}}return false;
}int main()
{int t;cin >> t;while (t--){idx = 0;cin >> n >> m;memset(h, -1, sizeof h);for (int i = 0; i < m; i++){int num1, num2, num3;cin >> num1 >> num2 >> num3;if (num3 >= 0){add(num1, num2, num3);add(num2, num1, num3);}else add(num1, num2, num3);}if (spfa()) cout << "YES" << endl;else cout << "NO" << endl;}
}相关文章:

B - 负环
题目描述 给定一个 n 个点的有向图,请求出图中是否存在从顶点 11 出发能到达的负环。 负环的定义是:一条边权之和为负数的回路。 输入格式 本题单测试点有多组测试数据。 输入的第一行是一个整数 T,表示测试数据的组数。对于每组数据的格…...
)
居中一个元素(水平+垂直居中)
我们的示例代码全在此基础上修改: ...... <style>* {margin: 0;padding: 0;}.par {width: 600px;height: 400px;background-color: antiquewhite;display: flex;justify-content: center;align-items: center;}.chi1 {width: 60px;height: 40px;backgrou…...

React笔记(二)JSX
一、JSX JSX是javascript XML的简写,实际上是javascript的扩展,既有javascript的语法结构,又有XML的结构 1、JSX的规则要求 jsx必须要有一个根节点 如果不想产生无用的根标签,但是还要遵守JSX的语法的要求,可以使用…...

[多标签分类]MultiLabelBinarizer: 从one-hot 到multi-hot
]MultiLabelBinarizer: 从one-hot 到multi-hot 背景知识One hot encoderLabelEncoderMultiLabelBinarizer总结 背景知识 多类别分类: label space至少有3个label, 且默认每个sample有一个label, 与之相对应的是二元分类Binary classification, 多标签分类: 每个sample有1至多…...

【校招VIP】前端算法考察之排序
考点介绍: 不同的场景中,不同的排序算法执行效率不同。 稳定:冒泡、插入、归并 不稳定:选择、快速、堆排序、希尔排序 『前端算法考察之排序』相关题目及解析内容可点击文章末尾链接查看! 一、考点题目 1、使用js实…...
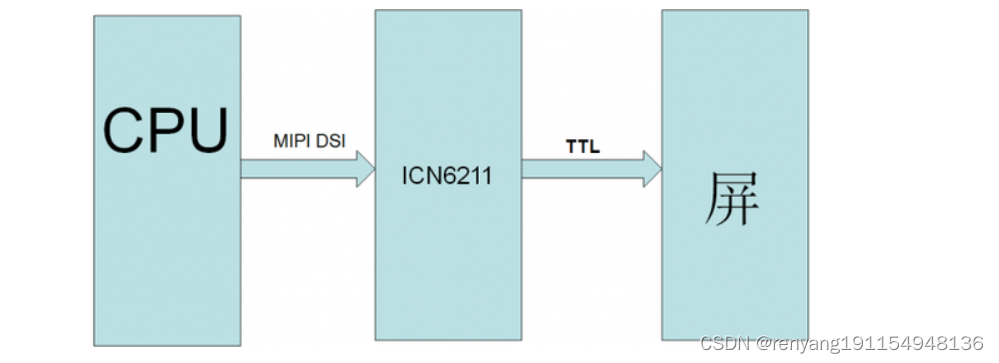
集创北方ICN6211 是一款MIPIDSI转RGB视频桥接IC
ICN6211 1.描述: ICN6211是一个桥接芯片,它接收MIPIDSI输入并发送RGB输出。MIPIDSI最多支持4个车道, 每个车道的最大运行频率为1Gbps;总最大输入带宽为4Gbps;并且还支持MIPI定义的ULPS(超 低功耗状态&a…...

SMT制造中的产品质量检验和管理
SMT制造中的质量检验和产品物料管理都是实现高质量、低成本、高效益的重要方法。在SMT加工的过程中,产品质量的检验和质量把控都是重中之重,可以有效的降低产品不良率及返修等造成制造成本升高的风险问题,今天就来跟大家讨论一下SMT制造中我们…...
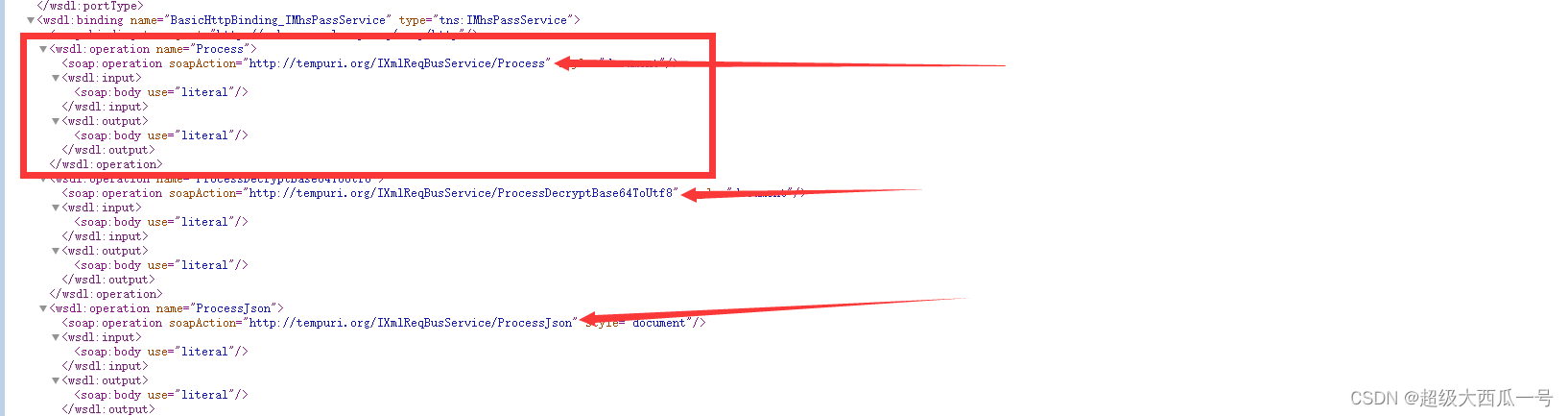
对接webservice接口时报错:发送方和接收方 Action 不匹配
趁着早上有时间,赶紧记录一下,哈哈。 错误提示如下: 1、英文版: <s:Envelope xmlns:s“http://schemas.xmlsoap.org/soap/envelope/”><s:Body><s:Fault>a:ActionNotSupportedThe message with Action ‘’ ca…...

python实现/直播服务器/聊天服务器/的多种解决方案
python有哪些技术栈 实现直播服务器 在Python中,您可以使用以下技术栈来实现直播服务器: Flask:Flask是一个轻量级的Web框架,可用于构建直播服务器的后端。您可以使用Flask编写API端点来处理直播流的控制和管理。 Django…...

PbootCMS 3.0.4 SQL注入
1.漏洞复现 PbootCMS 3.0.4,下载仓库 星梦/PbootCMS - Gitee.com 复现 漏洞页面:http://127.0.0.1/?search 或 http://127.0.0.1/?keyword POST请求:1select 1 2.正向分析 从可见功能点正向分析 index.php ... // 引用内核启动文件…...
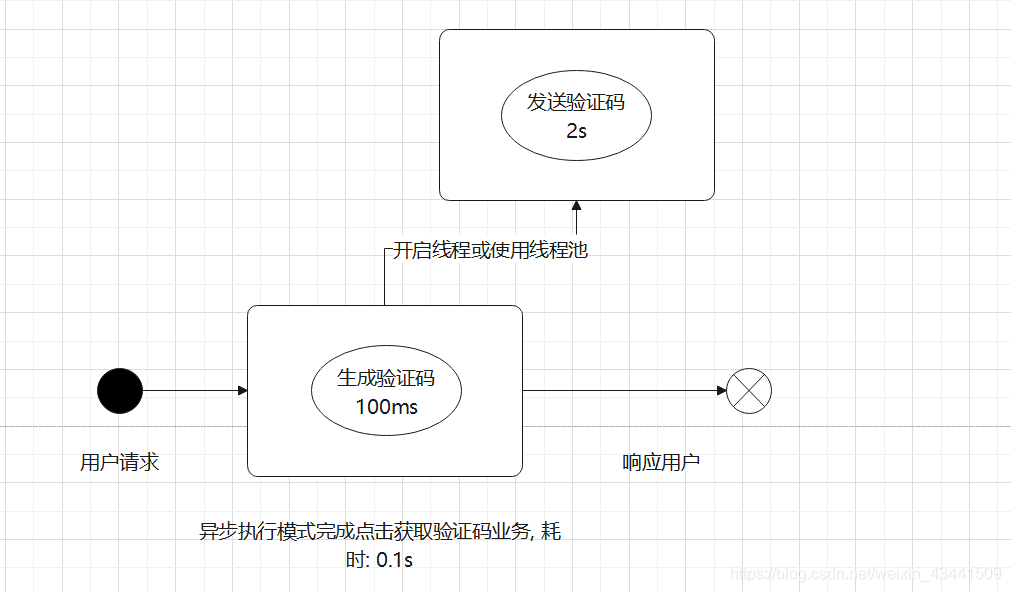
SpringBoot异步方法支持注解@Async应用
SpringBoot异步方法支持注解Async应用 1.为什么需要异步方法? 合理使用异步方法可以有效的提高执行效率 同步执行(同在一个线程中): 异步执行(开启额外线程来执行): 2.SpringBoot中的异步方法支持 在SpringBoot中并不需要我们自己去创建维护线程或者线程池来…...

UI/UX设计与前端开发:从零到一打造完美用户体验
引言 在当今的软件开发领域,UI/UX设计和前端开发是两个密不可分的环节。UI/UX设计师负责创造出直观、美观、用户友好的界面,而前端开发者则将这些设计转化为实际的、可交互的网页或应用。本文将深入探讨这两个领域的交集,并通过代码示例来展…...
Hadoop Hdfs基本命令
0目录 1.hadoop安装问题处理 2.hdfs基本命令 3.上传/下载文件和文件夹 1.hadoop安装问题处理 如果安装有进程无法启动,如下图 重新检查6个配置文件 Core-site.xml \ hdfs-site.xml \ hadoop-env.sh \ yarn-site.xml \ workers \ yarn-site.xml 来到hadoop313目录…...
Spring Boot 整合MyBatis(超详细)
😀前言 本篇博文关于Spring Boot 整合MyBatis,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家,您的满意是我的动力&#x…...

【管理运筹学】第 6 章 | 运输问题(4,表上作业法 |闭回路调整法以及特殊情况 | 产销不平衡的运输问题)
文章目录 引言二、表上作业法2.3 改进的方法 —— 闭回路调整法2.4 表上作业法中的特殊情况(一)无穷多最优解(二)退化 三、产销不平衡的运输问题3.1 产量大于销量3.2 销量大于产量 写在最后 引言 接下来我们学习表上作业法的最后…...

Greenplum实用技巧
一、通过gp_segment_id查看数据倾斜 gp_segment_id是表中的隐藏列,用来标记该行属于哪个segment节点。因此可以基于该隐藏列进行分组查询,获取每个segment的记录数,从而判断表数据的分布是否均匀或有倾斜。 qb#select gp_segment_id, count…...
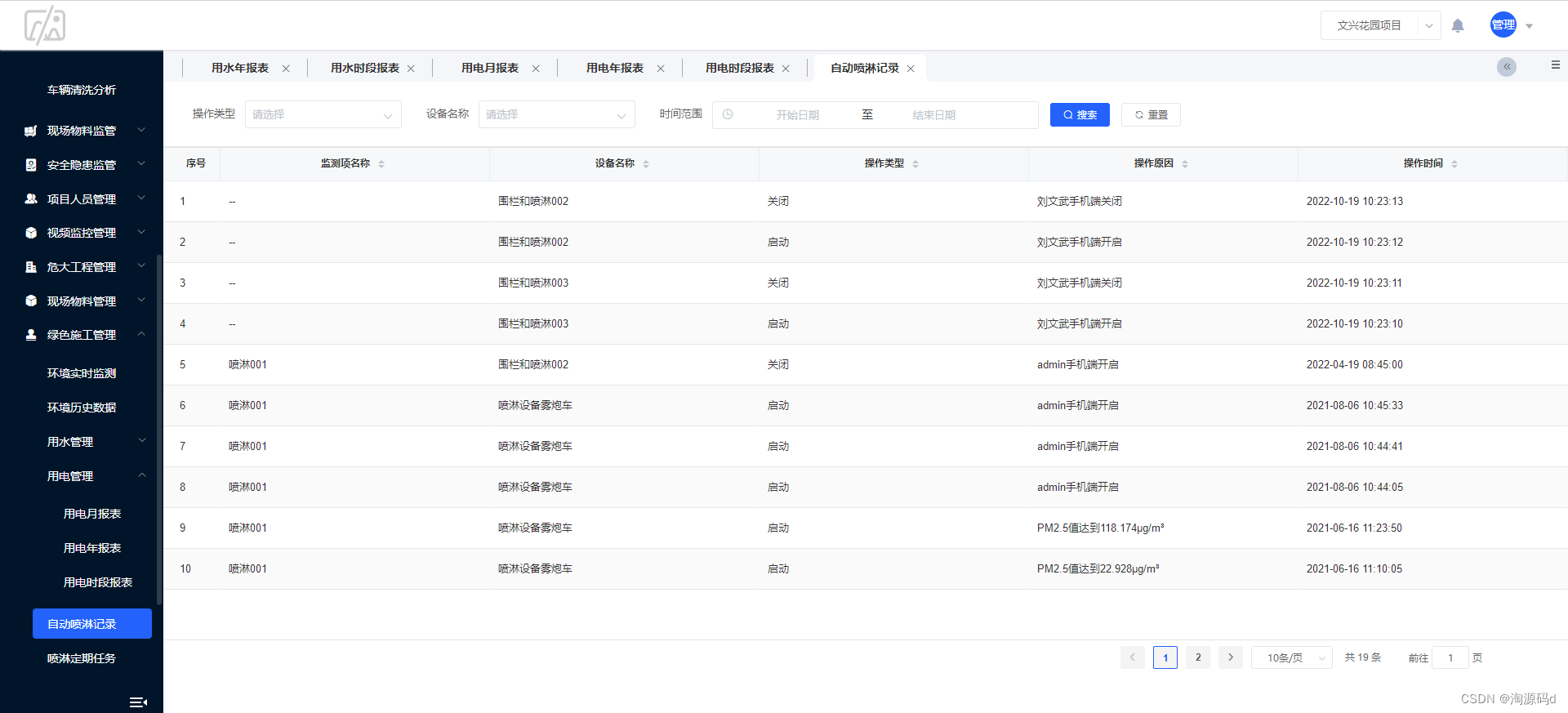
以物联网为核心的智慧工地云平台:聚集智能技术,实现建筑工地智慧管理
智慧工地云平台源码,智慧工地项目监管平台源码,智慧工地可视化数据大屏源码 智慧工地云平台是将云计算、大数据、物联网、移动技术和智能设备等信息化技术手段,聚集在建筑工地施工管理现场,围绕人员、机械、物料、环境等关键要素&…...
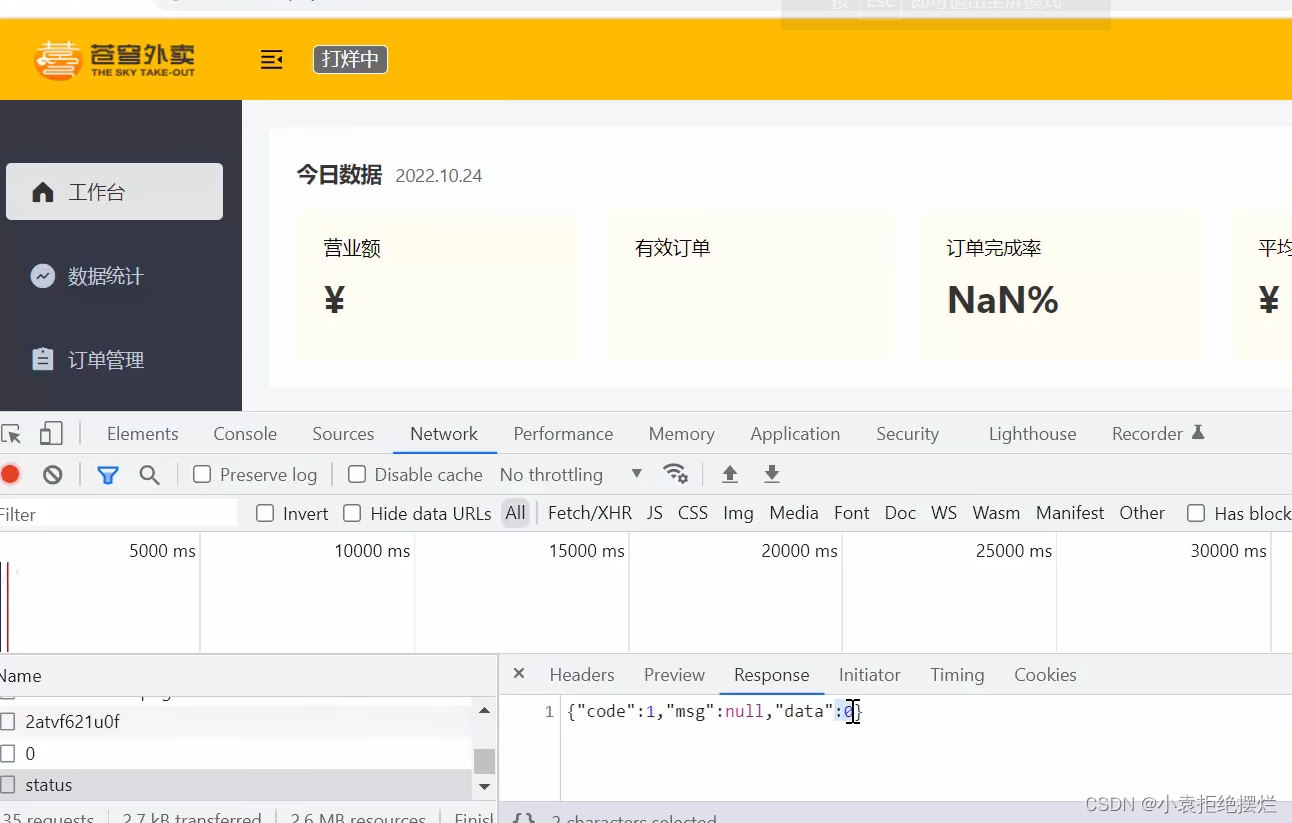
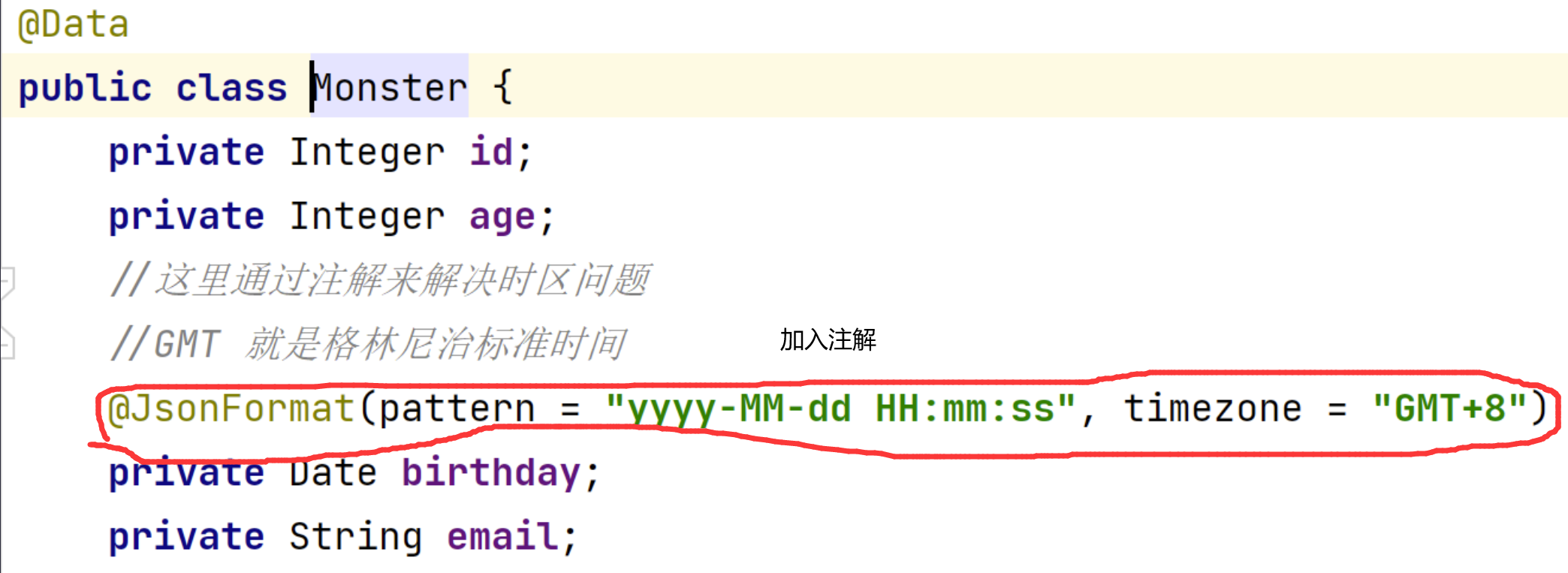
Java项目-苍穹外卖-Day05-Redis技术应用
1.店铺营业状态设置 需求分析和设计 左上角要求是有回显的 所以至少两个接口 1.查询营业状态接口(分为了管理端和用户端) 2.修改营业状态接口 因为管理端和用户端路径不同,所以现在是至少三个接口的 可以发现如果存到表里除了id只有一个…...

linux安装jmeter
linux安装jmeter 部署java1.8 下载jmeter安装包:官网、网盘5.6.2版本 # 解压 rootiZbp1at7nu2rpq4xn4zaf1Z:/opt/jmeter# sudo tar -xzf apache-jmeter-5.6.2.tgz # 加入环境变量 rootiZbp1at7nu2rpq4xn4zaf1Z:/opt/jmeter/apache-jmeter-5.6.2# export JMETER/op…...

【笔记】泛型以及如何绕过泛型定义
泛型定义以及其带来的好处 泛型使类型(类和接口)能够在定义类、接口和方法时成为参数。与方法声明中使用的更熟悉的形式参数非常相似,类型参数为您提供了一种通过不同输入重复使用相同代码的方法。区别在于形式参数的输入是值,而…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
