linux系统(centos、ubuntu、银河麒麟服务、uos、deepin)判断程序是否已安装,通用判断方法:适用所有应用和命令的判断
前言
项目中需要判断linux服务器中是否已经安装了某个服务
方法有很多种,但是很多都不通用, 脚本代码就不容易做成统一的
解决方案
用下面的脚本代码去进行判断
用jdk测试
脚本意思如下:
输入java -version命令,将返回的字符串输出第一行
如果里面包含java version这个字符串则说明jdk已经安装
if [[ $(java -version 2>&1 |awk 'NR==1') =~ "java version" ]]
thenecho "jdk已安装"
fi下图中我们可以看到输入java -version之后,返回的字符串里包含java version这个字符串,没安装的时候是不包含的,所以可以用这个脚本代码来判断是否已经安装

用mysql测试
脚本内容
if [[ $(mysql -V 2>&1 |awk 'NR==1') =~ "mysql Ver" ]]
thenecho "mysql已安装"
fi执行脚本提示mysql已经安装
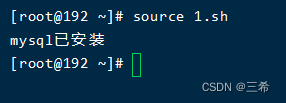
输入mysql -V 会返回的值

相关文章:

linux系统(centos、ubuntu、银河麒麟服务、uos、deepin)判断程序是否已安装,通用判断方法:适用所有应用和命令的判断
前言 项目中需要判断linux服务器中是否已经安装了某个服务 方法有很多种,但是很多都不通用, 脚本代码就不容易做成统一的 解决方案 用下面的脚本代码去进行判断 用jdk测试 脚本意思如下: 输入java -version命令,将返回的字…...
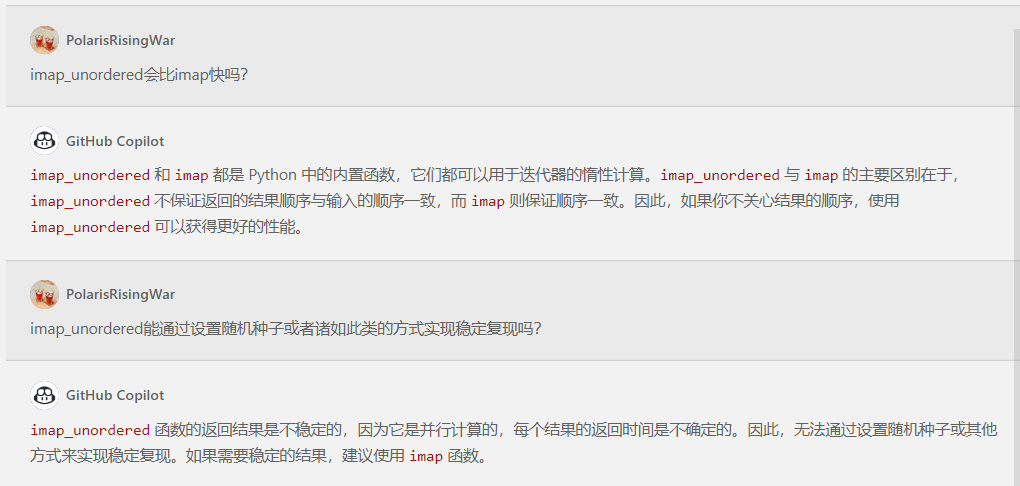
Python3多线程/多进程解决方案(持续更新ing...)
诸神缄默不语-个人CSDN博文目录 文章目录 1. 多线程2. 多进程示例1:multiprocessing.Pool直接实现对一个列表中的每个元素的函数操作示例2:使用苏神写的工具函数实现对一个迭代器中每个元素的函数操作 1. 多线程 2. 多进程 示例1:multiproc…...

在`CentOS`中安装`Docker Engine`
本文总结如何在CentOS中安装Docker Engine 〇、Docker Engine 介绍 Docker Engine是一种开源容器化技术,用于构建和容器化应用程序。Docker引擎作为一个客户端-服务器应用程序: 具有长时间运行守护进程的服务器。指定接口的api,程序可以使用这些接口与…...
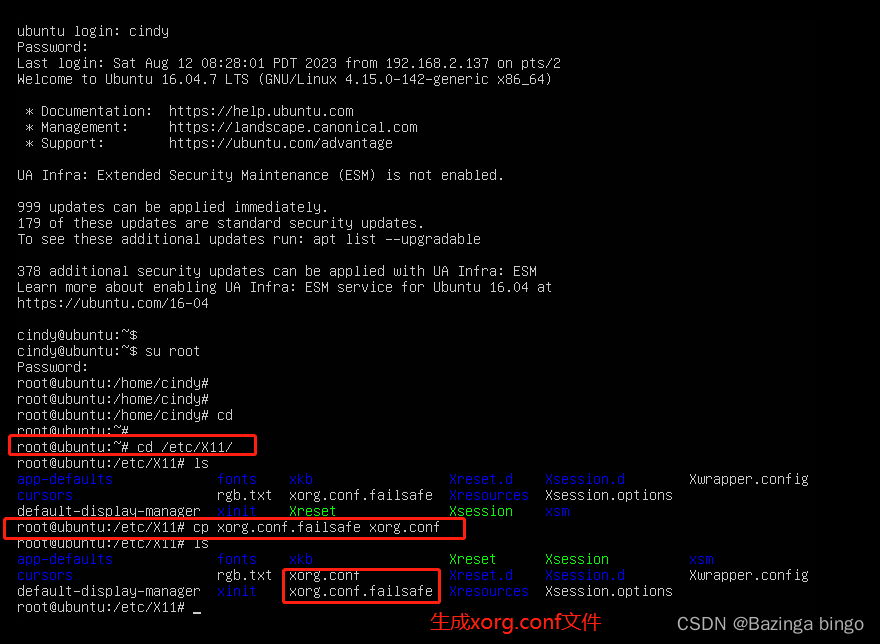
[ VMware 虚拟机 ] 启动不了图形界面,报 “The system is running in low-graphics mode” 错误
文章目录 问题现象异常原因解决方案 问题现象 在启动虚拟机的时候,不能正常的进入图形界面,报 “The system is running in low-graphics mode” 错误。 异常原因 启动界面的xorg.conf文件失败并删除。 解决方案 1、点击异常界面上的 “ok”后&…...
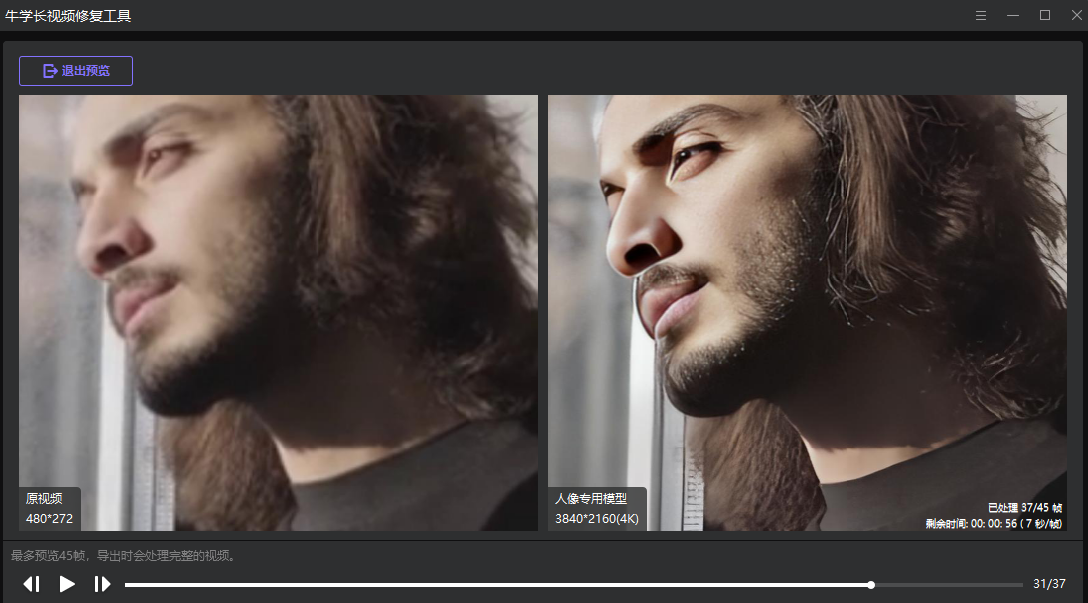
如何提高视频清晰度?视频调整清晰度操作方法
现在很多小伙伴通过制作短视频发布到一些短视频平台上记录生活,分享趣事。但制作的视频有些比较模糊,做视频的小伙伴应该都知道,视频画质模糊不清,会严重影响观众的观看体验。 通过研究,总结了以下几点严重影响的点 …...

IO进程线程,文件与目录,实现linux任意目录下ls -la
注意文件的名字、路径是如何输入的。 函数opendir打开目录,struct dirent,struct stat这些结构体的含义。 readdir()函数是一个用于读取目录内容的系统调用或库函数,在类Unix操作系统中(如Linux)广泛使用。它用于遍历…...
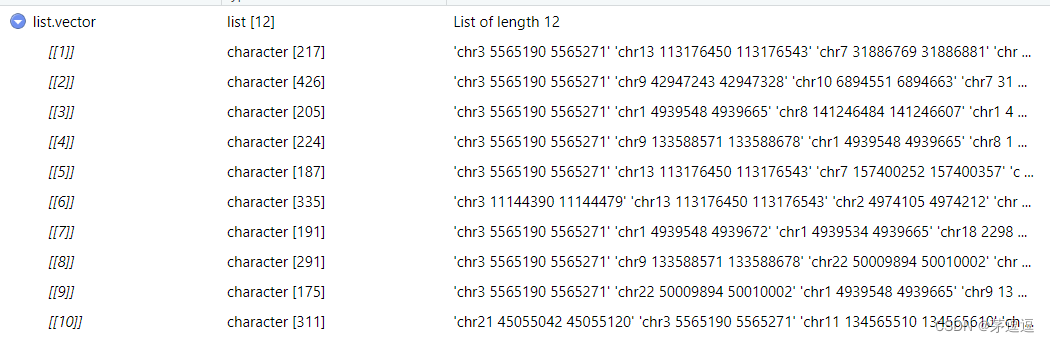
R语言如果列表中有列表,且每个子列表有一个向量:如何转变为仅仅一个列表里面含有向量
引言 有些时候,比如批量读取表格中的某一列的时候,最终你会得到列表里面装列表,且每个列表里面只有一个向量的情况。我们的目标是不要中间这一层列表,而是直接变成列表-向量这种简单的结构,如何完成呢。我觉得有很多方…...
nrm管理源仓库及发布私人npm包
使用nrm管理源及切换源仓库 1.安装nrm源管理器 npm install nrm -g2.查看目前现有的源仓库 通过 nrm ls 查看现有的源 nrm ls 输出:这是目前现有的源 3.切换不同的源 可以通过 nrm use xxx(源仓库名)来切换不同的源地址 nrm use taobao…...

云计算——虚拟化中的网络架构与虚拟网络(文末送书)
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 公众号:网络豆 座右铭:低头赶路,敬事如仪 个人主页: 网络豆的主页 目录 前期回顾 前言 一.网卡虚拟化 1.网卡虚拟化方法&…...

B - 负环
题目描述 给定一个 n 个点的有向图,请求出图中是否存在从顶点 11 出发能到达的负环。 负环的定义是:一条边权之和为负数的回路。 输入格式 本题单测试点有多组测试数据。 输入的第一行是一个整数 T,表示测试数据的组数。对于每组数据的格…...
)
居中一个元素(水平+垂直居中)
我们的示例代码全在此基础上修改: ...... <style>* {margin: 0;padding: 0;}.par {width: 600px;height: 400px;background-color: antiquewhite;display: flex;justify-content: center;align-items: center;}.chi1 {width: 60px;height: 40px;backgrou…...

React笔记(二)JSX
一、JSX JSX是javascript XML的简写,实际上是javascript的扩展,既有javascript的语法结构,又有XML的结构 1、JSX的规则要求 jsx必须要有一个根节点 如果不想产生无用的根标签,但是还要遵守JSX的语法的要求,可以使用…...

[多标签分类]MultiLabelBinarizer: 从one-hot 到multi-hot
]MultiLabelBinarizer: 从one-hot 到multi-hot 背景知识One hot encoderLabelEncoderMultiLabelBinarizer总结 背景知识 多类别分类: label space至少有3个label, 且默认每个sample有一个label, 与之相对应的是二元分类Binary classification, 多标签分类: 每个sample有1至多…...

【校招VIP】前端算法考察之排序
考点介绍: 不同的场景中,不同的排序算法执行效率不同。 稳定:冒泡、插入、归并 不稳定:选择、快速、堆排序、希尔排序 『前端算法考察之排序』相关题目及解析内容可点击文章末尾链接查看! 一、考点题目 1、使用js实…...
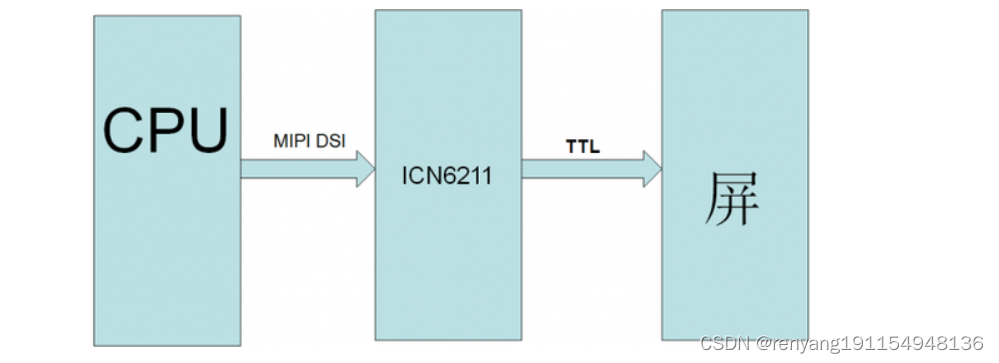
集创北方ICN6211 是一款MIPIDSI转RGB视频桥接IC
ICN6211 1.描述: ICN6211是一个桥接芯片,它接收MIPIDSI输入并发送RGB输出。MIPIDSI最多支持4个车道, 每个车道的最大运行频率为1Gbps;总最大输入带宽为4Gbps;并且还支持MIPI定义的ULPS(超 低功耗状态&a…...

SMT制造中的产品质量检验和管理
SMT制造中的质量检验和产品物料管理都是实现高质量、低成本、高效益的重要方法。在SMT加工的过程中,产品质量的检验和质量把控都是重中之重,可以有效的降低产品不良率及返修等造成制造成本升高的风险问题,今天就来跟大家讨论一下SMT制造中我们…...
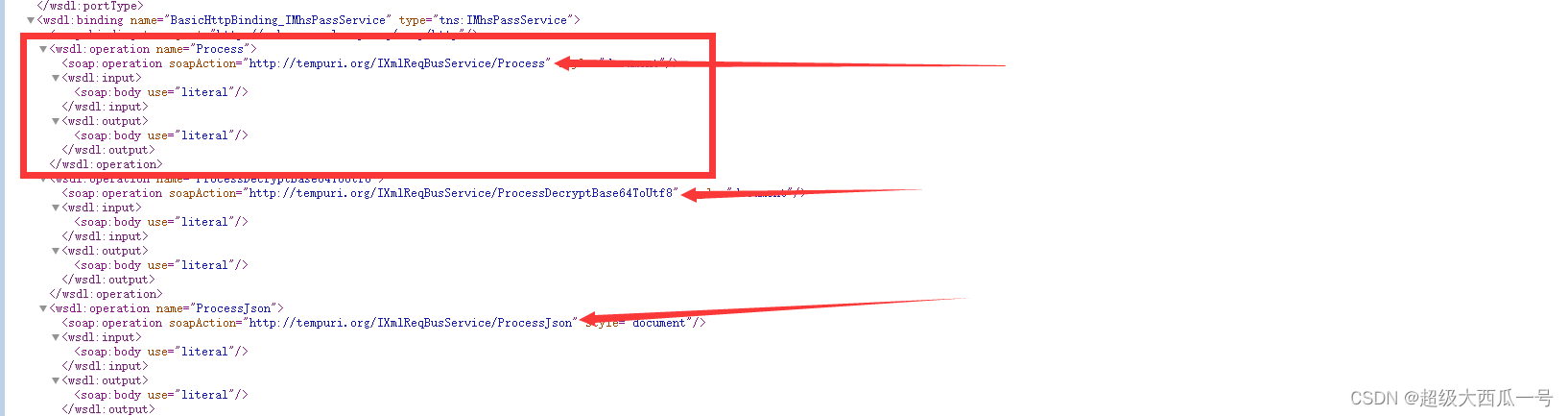
对接webservice接口时报错:发送方和接收方 Action 不匹配
趁着早上有时间,赶紧记录一下,哈哈。 错误提示如下: 1、英文版: <s:Envelope xmlns:s“http://schemas.xmlsoap.org/soap/envelope/”><s:Body><s:Fault>a:ActionNotSupportedThe message with Action ‘’ ca…...

python实现/直播服务器/聊天服务器/的多种解决方案
python有哪些技术栈 实现直播服务器 在Python中,您可以使用以下技术栈来实现直播服务器: Flask:Flask是一个轻量级的Web框架,可用于构建直播服务器的后端。您可以使用Flask编写API端点来处理直播流的控制和管理。 Django…...

PbootCMS 3.0.4 SQL注入
1.漏洞复现 PbootCMS 3.0.4,下载仓库 星梦/PbootCMS - Gitee.com 复现 漏洞页面:http://127.0.0.1/?search 或 http://127.0.0.1/?keyword POST请求:1select 1 2.正向分析 从可见功能点正向分析 index.php ... // 引用内核启动文件…...
SpringBoot异步方法支持注解@Async应用
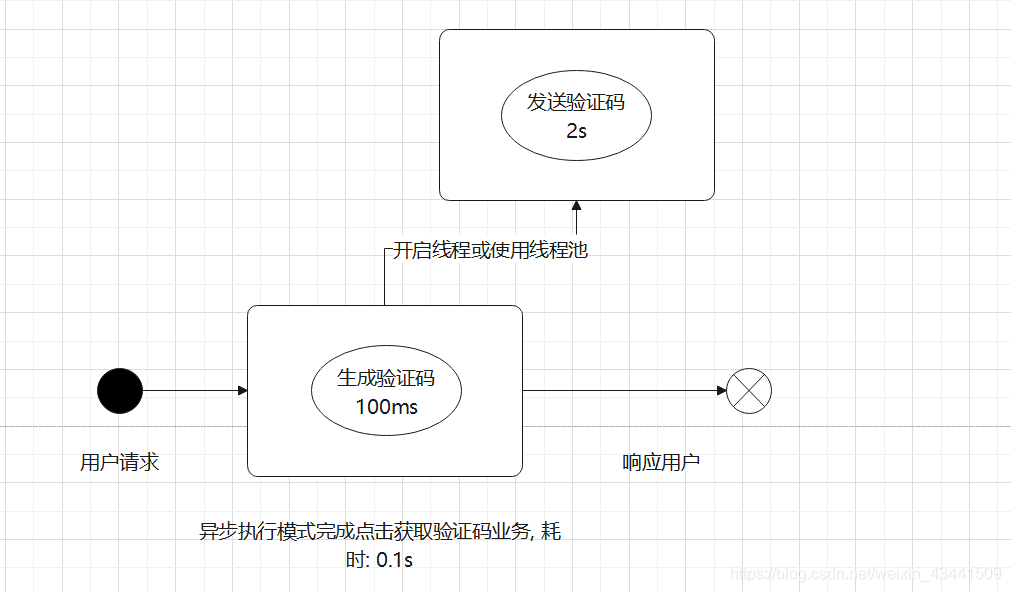
SpringBoot异步方法支持注解Async应用 1.为什么需要异步方法? 合理使用异步方法可以有效的提高执行效率 同步执行(同在一个线程中): 异步执行(开启额外线程来执行): 2.SpringBoot中的异步方法支持 在SpringBoot中并不需要我们自己去创建维护线程或者线程池来…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
