【记录】USSOCOM Urban3D 数据集读取与处理
Urban3D数据集内容简介
Urban3D数据集图像为正摄RGB影像,分辨率为50cm。
从SpaceNet上使用aws下载数据,文件夹结构为:
|- 01-Provisional_Train|- GT|- GT中包含GTC,GTI,GTL.tif文件,GTL为ground truth building footprint。|- Inputs|- Inputs中包含DSM,DTM,RGB.tif文件,DSM为Digital Surface Models,DTM为Digital Terrain Models,normalized DSM (nDSM = DSM - DTM)
|- 02-Provisional_Test
|- 03-Sequestered_Test
|- 04-Unused_Data
|- AOI_polygons
|- Pretrained_Models|- 包含前6名参赛团队的模型
每一块.tif大小为2048*2048。
Urban3D数据集读取
from torchvision import transforms
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import sys
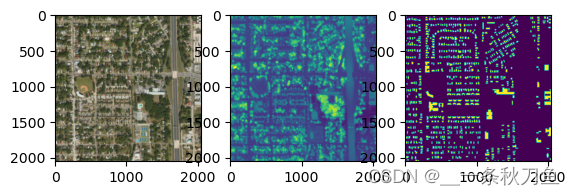
rgb = Image.open("/01-Provisional_Train/Inputs/JAX_Tile_016_RGB.tif")
dsm = Image.open("/01-Provisional_Train/Inputs/JAX_Tile_016_DSM.tif")
gtl = Image.open("/01-Provisional_Train/GT/JAX_Tile_016_GTL.tif")
print(rgb.size, dsm.size, gtl.size) >> (2048, 2048) (2048, 2048) (2048, 2048)
print(np.array(rgb).shape, np.array(dsm).shape, np.array(gtl).shape) >> (2048, 2048, 3) (2048, 2048) (2048, 2048)
print(np.array(rgb).dtype, np.array(dsm).dtype, np.array(gtl).dtype) >> uint8 float32 uint8fig = plt.figure()
plt.subplot(131)
plt.imshow(np.array(rgb))
plt.subplot(132)
plt.imshow(np.array(dsm))
plt.subplot(133)
plt.imshow(np.array(gtl))print(np.max(gtl), np.min(gtl)) >> 6, 2
Urban3D数据集Pytorch处理
使用深度学习需要对Urban3D数据进行裁剪,这里采用torchvision.transforms.RandomCrop进行裁剪。RandomCrop可以直接作用于PIL.Image打开的文件和torch类型的数据上,但不能作用于numpy数组。具体内容可以参考numpy, PIL, tensor类型在torchvision.transforms时使用
def type_convert(x):x_ = np.array(x).astype(np.float32)return x_
def to_tensor(x):x_ = np.expand_dims(x, axis=0)x_ = torch.from_numpy(x_)return x_
trans = transforms.Compose([transforms.RandomCrop(size=256),transforms.Lambda(type_convert),transforms.Lambda(to_tensor)
])torch.random.manual_seed(16)
rgb_crop = trans(rgb)
torch.random.manual_seed(16)
dsm_crop = trans(dsm)
torch.random.manual_seed(16)
gtl_crop = trans(gtl)
print(rgb_crop.size(), dsm_crop.size(), gtl_crop.size())
fig = plt.figure()
plt.subplot(131)
plt.imshow(rgb_crop[0,:,:,0])
plt.subplot(132)
plt.imshow(dsm_crop[0,:,:])
plt.subplot(133)
plt.imshow(gtl_crop[0,:,:])
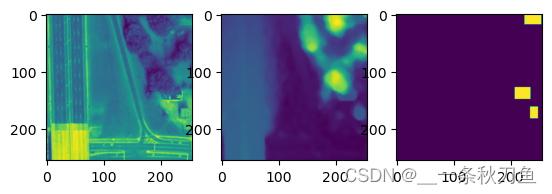
同时还需要注意的一点是为了保证RandomCrop后data和label的一致性,需要设置随机数种子。对于GTL需要改变label的值。
def type_convert_gtl(x):x_ = np.array(x).astype(np.float32)x_[x_==6]=1x_[x_==2]=0return x_
相关文章:

【记录】USSOCOM Urban3D 数据集读取与处理
Urban3D数据集内容简介 Urban3D数据集图像为正摄RGB影像,分辨率为50cm。 从SpaceNet上使用aws下载数据,文件夹结构为: |- 01-Provisional_Train|- GT|- GT中包含GTC,GTI,GTL.tif文件,GTL为ground truth b…...

flutter ios webview不能打开http地址
参考 1、iOS添加信任 webview_flutter 在使用过程中会iOS出现无法加载HTTP请求的情况, 但是Flutter 却可以加载HTTP请求。这就与两个的框架有关了,Flutter是独立于UIKit框架的。 解决方案就是在iOS 的info.plist中添加对HTTP的信任。 <key>NSApp…...

【SpringBoot】详细介绍SpringBoot中Entity类中的getters和setters
在Spring Boot中的Entity类中,getters和setters是用来获取和设置对象属性值的方法。它们是Java Bean规范的一部分,并且通常被用于向开发人员和框架公开类的属性。 在Entity类中,getters和setters方法通常通过property来实现,即将…...
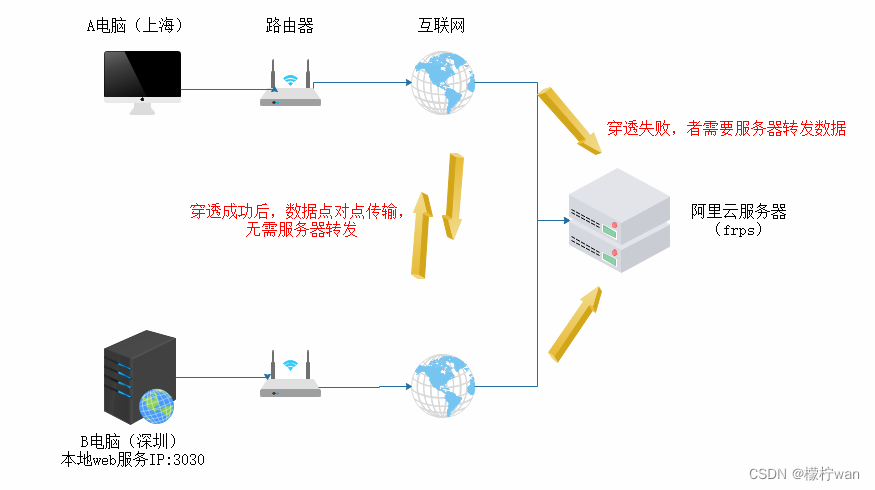
阿里云服务器搭建FRP实现内网穿透-P2P
前言 在了解frp - p2p之前,请先了解阿里云服务器搭建FRP实现内网穿透-转发: 文章地址 1、什么是frp - p2p frp(Fast Reverse Proxy)是一个开源的反向代理工具,它提供了多种功能,包括端口映射、流量转发和内网穿透等。…...
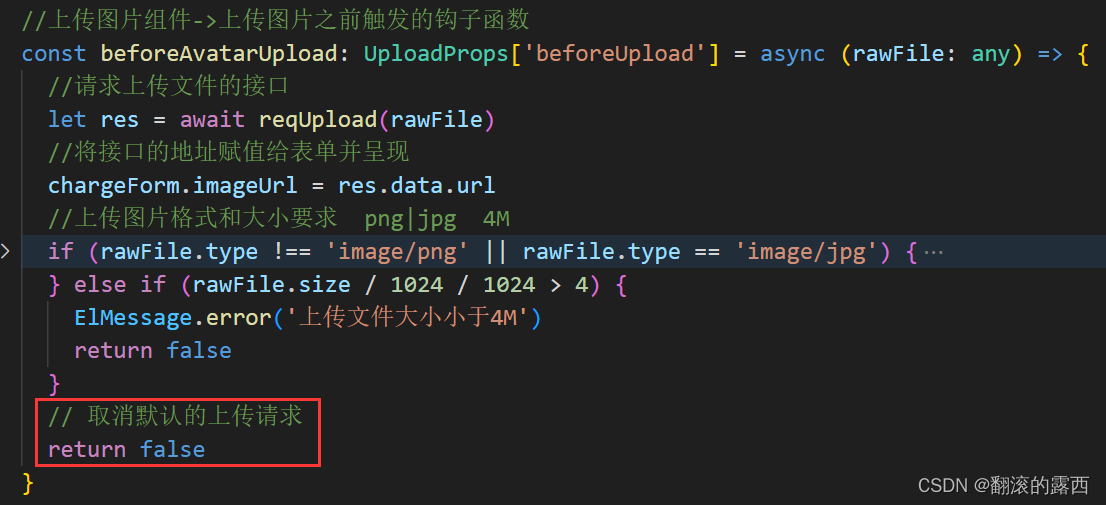
Vue3 Element-plus Upload 上传图片
技术栈:Vue3 Ts Element-plus 官网地址:Upload 上传 | Element Plus 一、背景: 表单上传图片功能 二、效果: 三、流程: ①点击上传图片按钮,系统弹出文件选择对话框,选择图片并确认 ②调…...

PCL | Ubuntu18安装CloudCompare
文章目录 操作教程 操作教程 CloudCompare下载官网:https://www.danielgm.net/cc/release/ 安装flatpak插件 sudo apt install flatpak添加库路径 flatpak remote-add flathub https://flathub.org/repo/flathub.flatpakrepo安装CC flatpak install flathub or…...
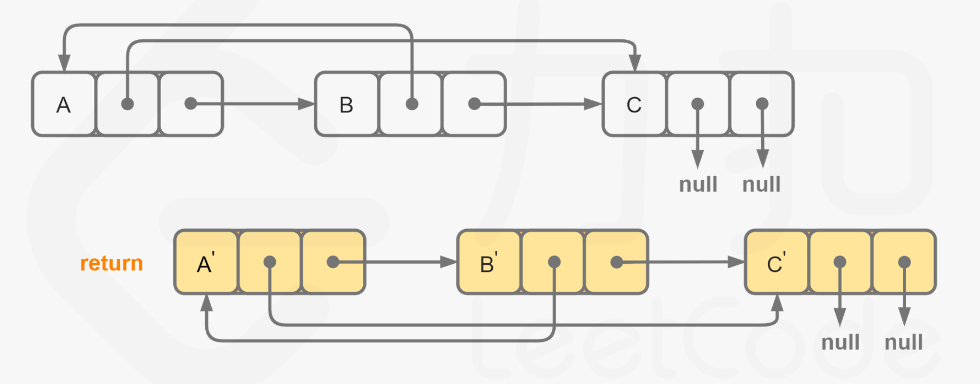
【LeetCode-中等题】138. 复制带随机指针的链表
文章目录 题目解题核心思路:找random指针指向思路一:哈希思路二:迭代构造新链表 方法一:哈希递归方法二:纯哈希方法三:迭代 节点拆分 题目 解题核心思路:找random指针指向 这里的拷贝属于深拷…...
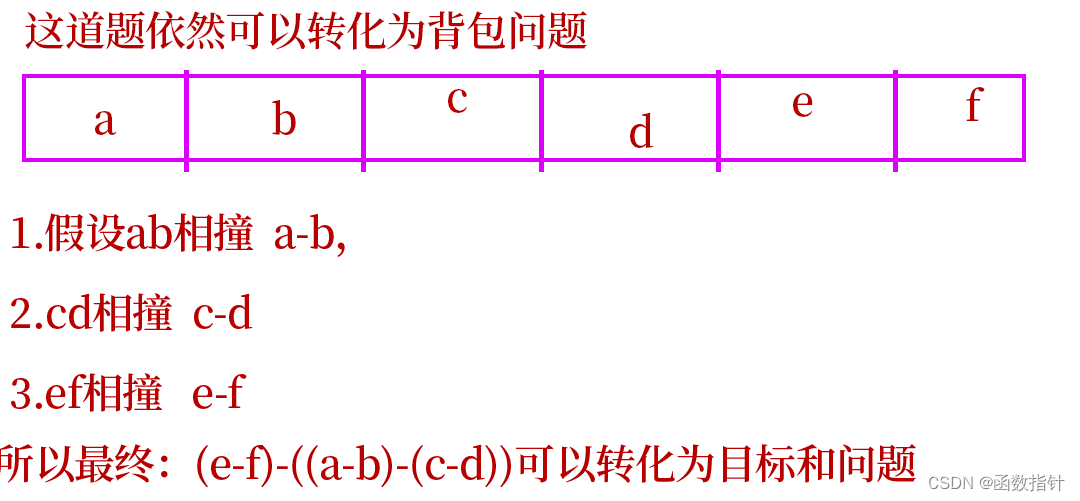
C++--动态规划背包问题(1)
1. 【模板】01背包_牛客题霸_牛客网 你有一个背包,最多能容纳的体积是V。 现在有n个物品,第i个物品的体积为vivi ,价值为wiwi。 (1)求这个背包至多能装多大价值的物品? (2)若背包恰好装满&a…...
【Android-Flutter】我的Flutter开发之旅
目录: 0、文档:1、在Windows上搭建Flutter开发环境(1)[使用中国镜像(❌详细看官方文档)](https://docs.flutter.dev/community/china)(2)[下载最新版Flutter SDK(已包含Dart)](https://docs.flu…...
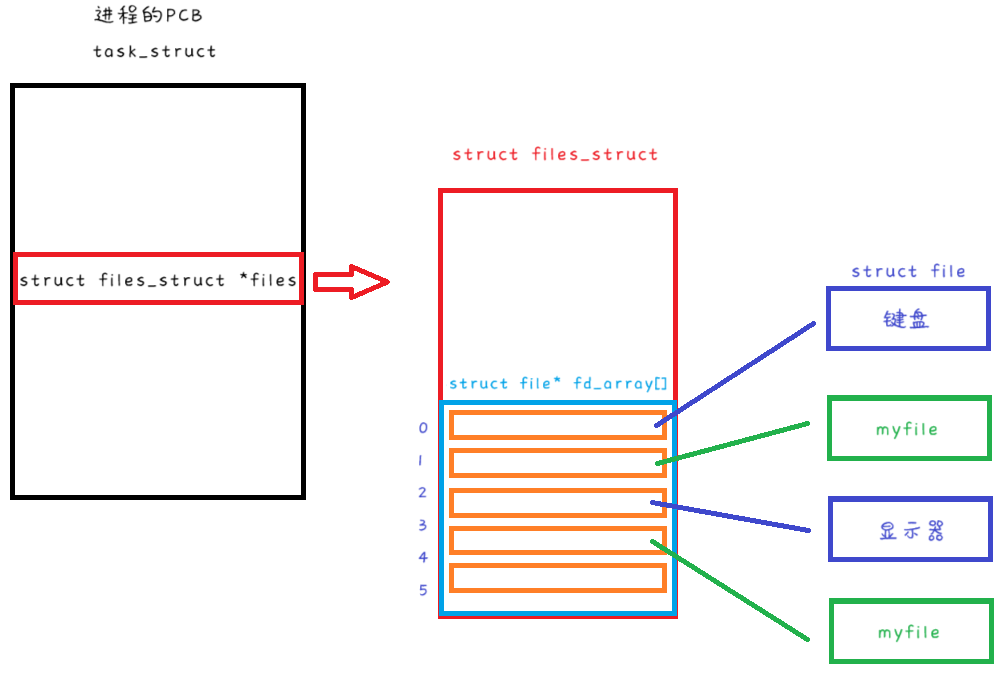
【Linux】深入理解文件操作
文章目录 初次谈论文件重温C语言文件操作系统文件操作接口openwriteread 再次谈论文件文件描述符文件描述符的分配规则 重定向什么是重定向重定向的本质系统调用接口实现重定向<、>、>> 初次谈论文件 开始之前先谈论一下关于文件的一些共识性问题。 一个文件可以…...
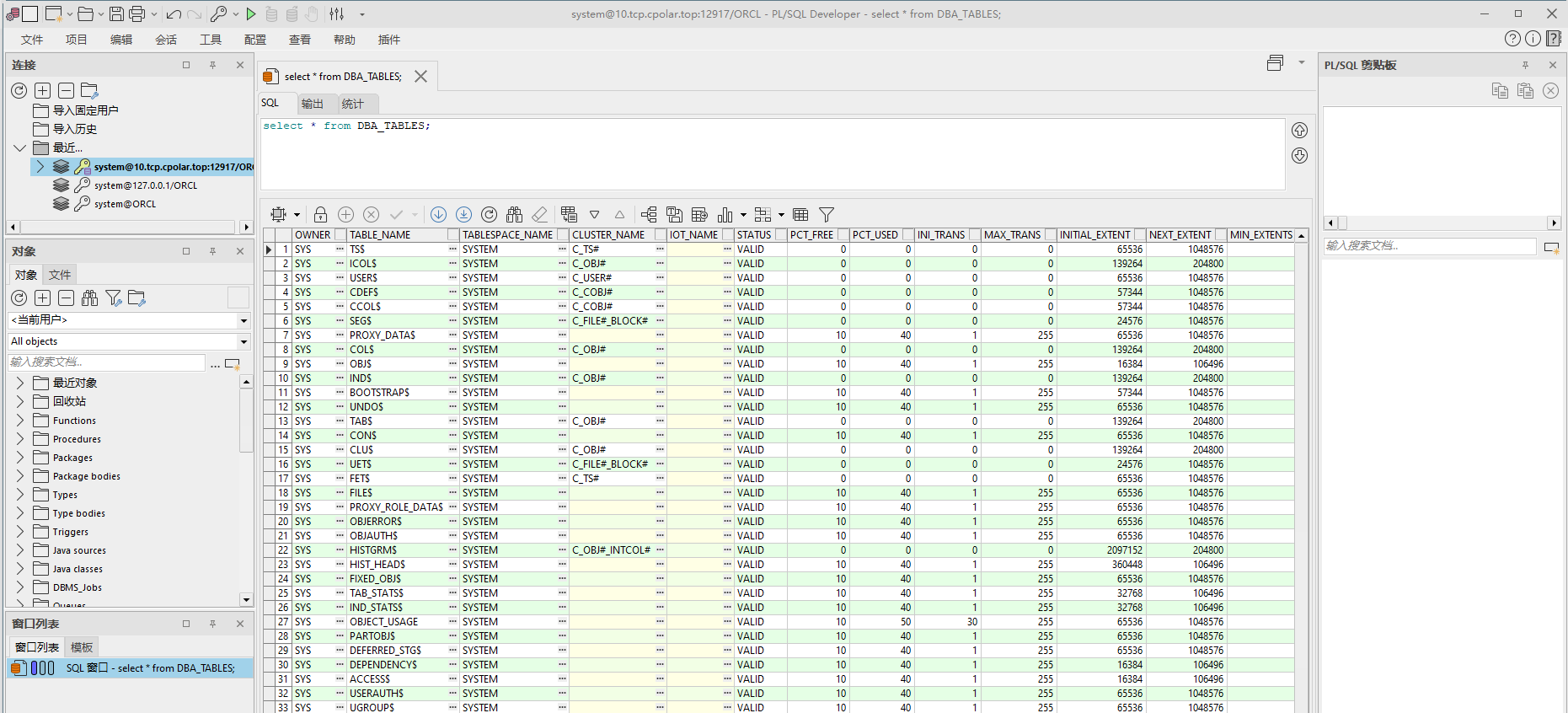
异地使用PLSQL远程连接访问Oracle数据库【内网穿透】
文章目录 前言1. 数据库搭建2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射 3. 公网远程访问4. 配置固定TCP端口地址4.1 保留一个固定的公网TCP端口地址4.2 配置固定公网TCP端口地址4.3 测试使用固定TCP端口地址远程Oracle 前言 Oracle,是甲骨文公司的一款关系…...

【方案】基于AI边缘计算的智慧工地解决方案
一、方案背景 在工程项目管理中,工程施工现场涉及面广,多种元素交叉,状况较为复杂,如人员出入、机械运行、物料运输等。特别是传统的现场管理模式依赖于管理人员的现场巡查。当发现安全风险时,需要提前报告࿰…...

华为各型号交换机开启SNMP v3
设备型号:华为S5720S-28P-LI-AC 设备软件版本:V200R011C10SPC600 调试命令: snmp-agent snmp-agent sys-info version v3 snmp-agent group v3 GroupName privacy //{GroupName}是设置一个SNMP的组名,我设置是SNMPGroup snm…...

CocosCreator3.8研究笔记(一)windows环境安装配置
一、安装Cocos 编辑器 (1)、下载Cocos Dashboard安装文件 Cocos 官方网站Cocos Dashboard下载地址 : https://www.cocos.com/creator-download9下载完成后会得到CocosDashboard-v2.0.1-win-082215.exe 安装文件,双击安装即可。 …...

【JavaWeb 专题】15个最经典的JavaWeb面试题
文章目录 HTTP长连接和短连接HTTP/1.1 与 HTTP/1.0 的区别可扩展性缓存带宽优化长连接消息传递Host 头域错误提示 AjaxAjax 的优势: JSP 和 servlet 有什么区别?定义区别 JSP 的9大内置对象及作用JSP 的 4 种作用域?session 和 cookie 有什么…...
)
力扣:75. 颜色分类(Python3)
题目: 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sort …...
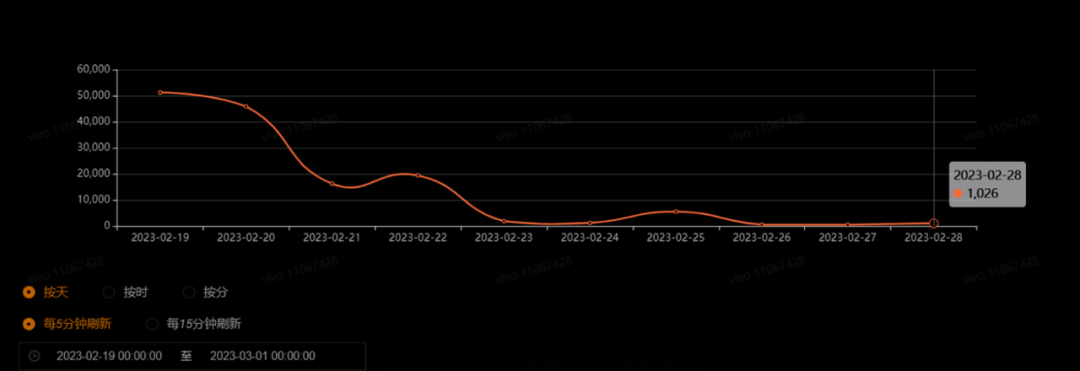
JVM 内存大对象监控和优化实践
作者:vivo 互联网服务器团队 - Liu Zhen、Ye Wenhao 服务器内存问题是影响应用程序性能和稳定性的重要因素之一,需要及时排查和优化。本文介绍了某核心服务内存问题排查与解决过程。首先在JVM与大对象优化上进行了有效的实践,其次在故障转移与…...

vue indexedDB 取指定数据库指定表 全部key用request.onsuccess
1 例子 export async function funcGetKey(dbName, tableName) {return new Promise((resolve, reject) > {// 打开指定的数据库const request indexedDB.open(dbName);request.onerror (event) > {console.error(打开数据库失败: , event.target.error);reject(event…...

Java 数据结构使用学习
Set和List的区别 Set 接口实例存储的是无序的,不重复的数据。List 接口实例存储的是有序的,可以重复的元素。 Set 检索效率低下,删除和插入效率高,插入和删除不会引起元素位置改变 <实现类有HashSet,TreeSet>。 List 和数…...
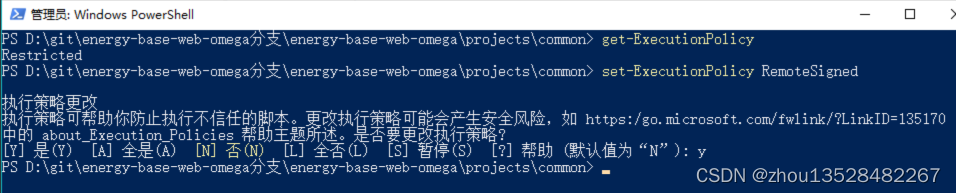
monorepo更新组件报错,提示“无法加载文件 C:\Program Files\nodejs\pnpm.ps1,因为在此系统上禁止运行脚本”
解决方法: 第一步:管理员身份运行 window.powershell, win x打开powerShell命令框,进入到对应项目路径。 第二步:执行:get-ExecutionPolicy,显示Restricted,表示状态是禁止的; 第…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
