【数据结构】排序(插入、选择、交换、归并) -- 详解
一、排序的概念及其运用
1、排序的概念
- 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
- 内部排序:数据元素全部放在内存中的排序。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
2、常见的排序算法
二、常见排序算法的实现
1、插入排序(Insertion Sort)
(1)基本思想
直接插入排序是一种简单的插入排序法,其基本思想是: 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中。重复这个过程,直到所有的记录插入完为止,得到一个新的有序序列 。
(2)直接插入排序(InsertSort)
当插入第 i (i >= 1) 个元素时,前面的 array[0],array[1],…,array[i-1] 已经排好序,此时用 array[i] 的排序码与 array[i-1],array[i-2],… 的排序码顺序进行比较,找到插入位置即将 array[i] 插入,原来位置上的元素顺序后移。

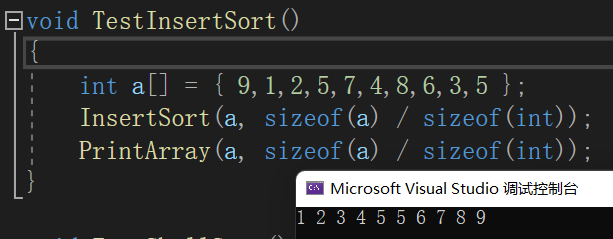
// 直接插入排序
void InsertSort(int* a, int n)
{assert(a);for (int i = 0; i < n - 1; ++i){// [0,end]有序,把end+1位置的值插入,保持有序int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end])//升序{a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}
a.插入排序是原地排序算法吗?
从实现过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以 空间复 杂度是 O(1) ,也就是说,这是一个 原地排序算法 。
b.插入排序是稳定的排序算法吗?
在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是 稳定 的排序算法。
c.插入排序的时间复杂度是多少?
如果要排序的数据已经是 有序 的,我们并不需要搬移任何数据。如果我们从尾到头在有序数据组里面查找插入位置,每次只需要比较一个数据就能确定插入的位置。所以这种情况下,最好是时间复杂度为 O(n) 。注意,这里是 从尾到头遍历已经有序的数据 。如果数组是 倒序 的,每次插入都相当于在数组的第一个位置插入新的数据,所以需要移动大量的数据,所以最坏情况时间复杂度为 O(n²) 。还记得在数组中插入一个数据的平均时间复杂度是多少吗?没错,是 O(n)。所以,对于插入排序来说,每次插入操作都相当于在数组中插入一个数据,循环执行 n 次插入操作,所以 平均时间复杂度为 O(n²) 。
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高。
- 时间复杂度:O(N²)。
- 空间复杂度:O(1),它是一种稳定的排序算法。
- 稳定性:稳定。
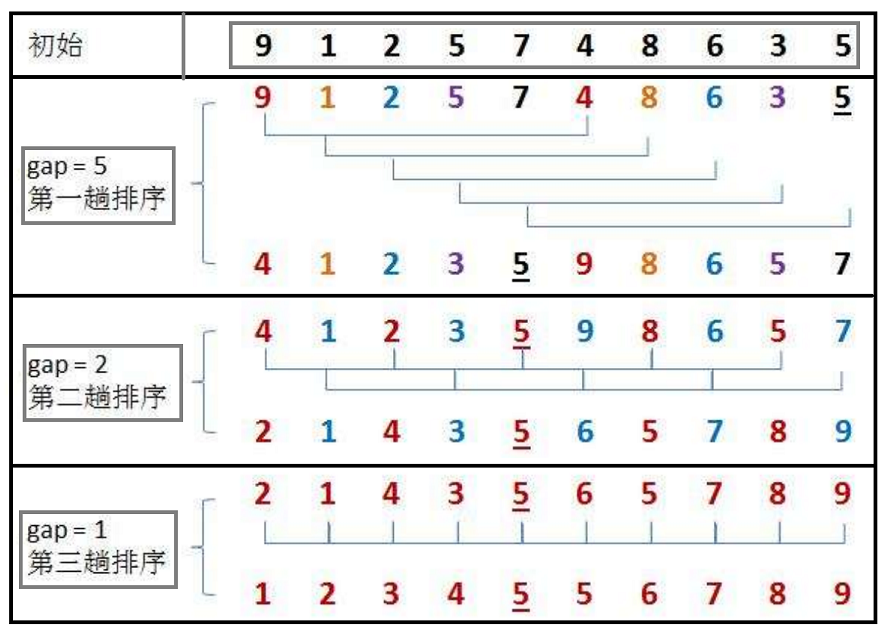
(3)希尔排序(ShellSort)(缩小增量排序)
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成若干个 组,所有距离为 gap 的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工 作。当到达 gap =1 时,所有记录在统一组内排好序。
// 希尔排序
void ShellSort(int* a, int n)
{assert(a);int gap = n;while (gap > 1) // 不能写成gap>0,因为gap的值始终>=1{gap = gap / 3 + 1;//gap = gap / 2;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
【关于 gap 的取值】
最初希尔提出的增量是 gap = n / 2,每一次排序完让增量减少一半 gap = gap / 2,直到 gap = 1 时排序相当于直接插入排序。直到后来 Knuth 提出的 gap = (gap / 3) + 1,每次排序让增量成为原来的三分之一,加一是防止 gap <= 3 时 gap = gap / 3 = 0 的发生,导致希尔增量最后不为1,无法完成插入排序。
选择 gap = (gap / 3) + 1 更稳定,能够尽可能地减少比较和交换的次数,以提高排序的效率。通过采用这种递减的方式,可以更好地分组元素,使得在每一轮排序中能够更快地将较小的元素移动到前面。序列被划分为较小的子序列,并通过插入排序的方式对每个子序列进行排序。这样做的好处是在初始阶段,较大的元素可以更快地向后移动,从而减少了后续比较和交换的次数。
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序的了,相当于直接插入,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度并不好计算,因为 gap 的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定,官方给出的时间复杂度是 O(N^1.3) 。
- 稳定性:不稳定。
《数据结构 (C 语言版 ) 》 --- 严蔚敏
《数据结构-用面相对象方法与C++描述》--- 殷人昆

【总结】
希尔排序在越大的数组上更能发挥优势,因为步子迈的更大,减少插入排序的移动次数更多。
2、选择排序
(1)基本思想
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每一次从待排序的数据元素中选出 最小(升序) / 最大(降序) 的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
(2)直接选择排序(SelectSort)
- 在元素集合 array[i] -- array[n-1] 中选择关键码最大 / 小的数据元素。
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。
- 在剩余的 array[i] -- array[n-2](array[i+1] -- array[n-1])集合中,重复上述步骤,直到集合剩余 1 个元素。

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 直接选择排序
void SelectSort(int* a, int n)
{assert(a);int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);// 如果begin和maxi重叠,那么要修正maxi的位置if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}
a.选择排序是原地排序算法吗?
选择排序空间复杂度为 O(1) ,是一种原地排序算法。
b.选择排序是稳定的排序算法吗?
答案是否定的,选择排序是一种 不稳定 的排序算法。选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样破坏了稳定性。 比如 4,9,4,1,8 这样一组数据,使用选择排序算法来排序的话,第一次找到最小元素 1 ,与第一个 4 交换位置,那第一个 4 和中间的 4 顺序就变了,所以就不稳定了.
c.选择排序的时间复杂度是多少?
选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为 O(n²)。
直接选择排序的特性总结:
- 效率不是很好,实际中很少使用。
- 时间复杂度:O(N²)。
- 空间复杂度:O(1)。
- 稳定性:不稳定。
(3)堆排序(HeapSort)
有关堆(Heap)的相关内容详解,具体请看:【数据结构】堆(Heap)_炫酷的伊莉娜的博客-CSDN博客
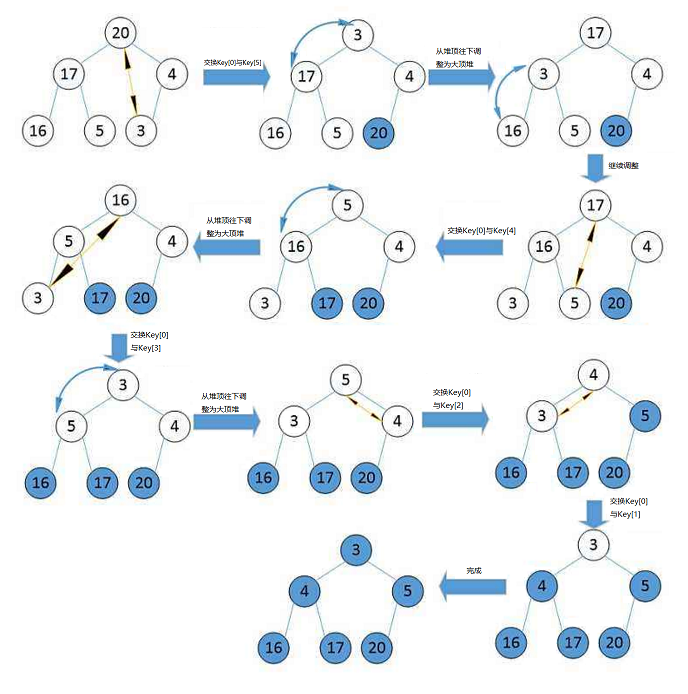
堆排序 (Heapsort) 是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是 排升序要建大堆,排降序建小堆 。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){//选出左右孩子中大的那个if (child + 1 < size && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆排序
void HeapSort(int* a, int n)
{assert(a);for (int i = ((n - 1) - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
直接选择排序的特性总结:
- 堆排序使用堆来选数,效率就高了许多。
- 时间复杂度:O(N*logN)。
- 空间复杂度:O(1)。
- 稳定性:不稳定。
3、交换排序
(1)基本思想
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将较大值向序列的尾部移动,将较小值向序列的前部移动。
(2)冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。
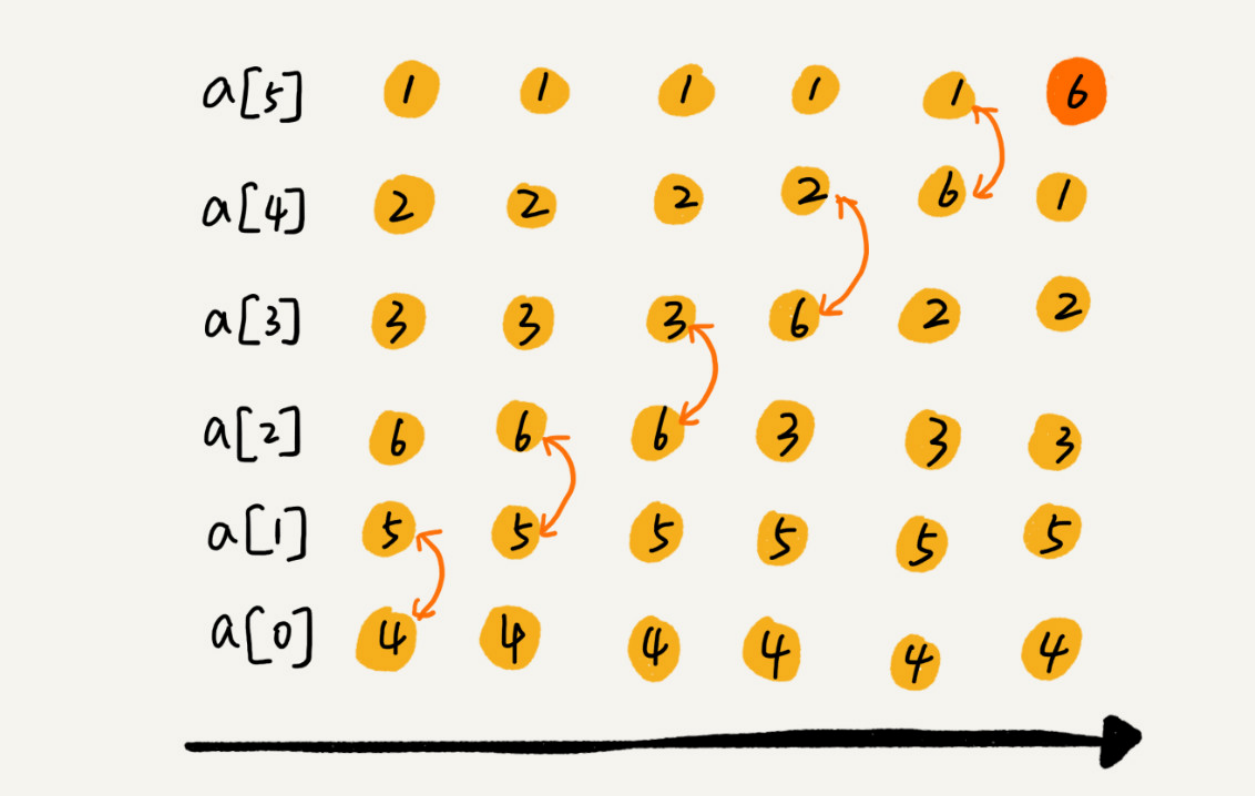
可以看出,经过一次冒泡操作之后,6 这个元素已经存储在正确的位置上。要想完成所有数据的排序,我们只要进行 6 次这样的冒泡操作就行了。

实际上,刚讲的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。下面再举一个例子,这里面给 6 个元素排序,只需要 4 次冒泡操作就可以了。

// 冒泡排序
void BubbleSort(int* a, int n)
{assert(a);for (int j = 0; j < n - 1; ++j){int exchange = 0; // 提前退出冒泡循环的标志for (int i = 1; i < n - j; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1; // 表示有数据交换}}if (exchange == 0) // 没有数据交换,提前退出{break;}}
}
a.冒泡排序是原地排序算法吗?
冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1) ,是一个原地排序算法。
b.冒泡排序是稳定的排序算法吗?
在冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定 性,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是 稳定 的排序算法。
c.冒泡排序的时间复杂度是多少?
最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束 了,所以最好情况时间复杂度是 O(n) 。而最坏的情况是,要排序的数据刚好是倒序排列的,我们需要进行 n 次冒泡操作,所以最坏情况时间复杂度为 O(n²) 。
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序。
- 时间复杂度:O(N²)。
- 空间复杂度:O(1)。
- 稳定性:稳定。
(3)快速排序法(Quicksort)
快速排序算法(Quicksort),我们习惯性把它简称为“快排”。快排利用的是分治思想。快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法,其基本思想为: 任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止 。
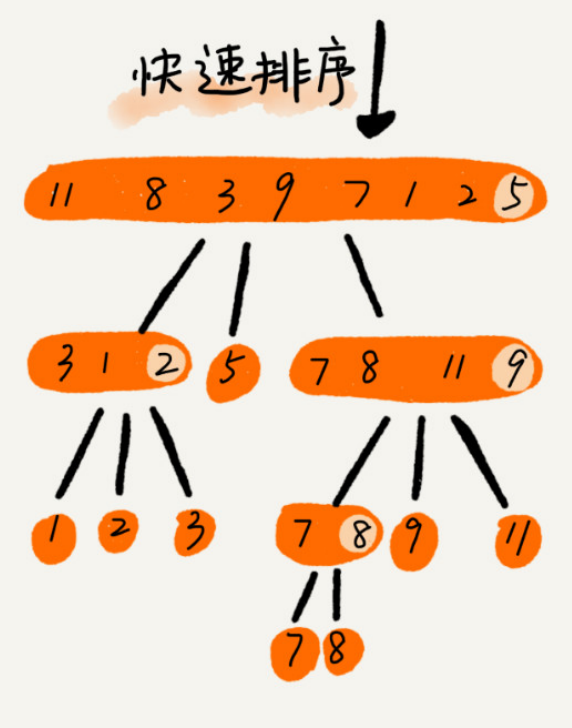
快排的处理过程是由上到下 的,先分区,然后再处理子问题。
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1){return;}// 按照基准值对array数组的[left, right)区间中的元素进行划分int div = partion(array, left, right); // 分区函数// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)// 递归排[left, div)QuickSort(array, left, div);// 递归排[div+1, right)QuickSort(array, div+1, right);
}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后续只需分析如何按照基准值来对区间中数据进行划分的方式即可。
将区间按照基准值划分为左右两半部分的常见方式有: (注意这三种方法 首次单趟后不一定相同)
a.hoare 版本
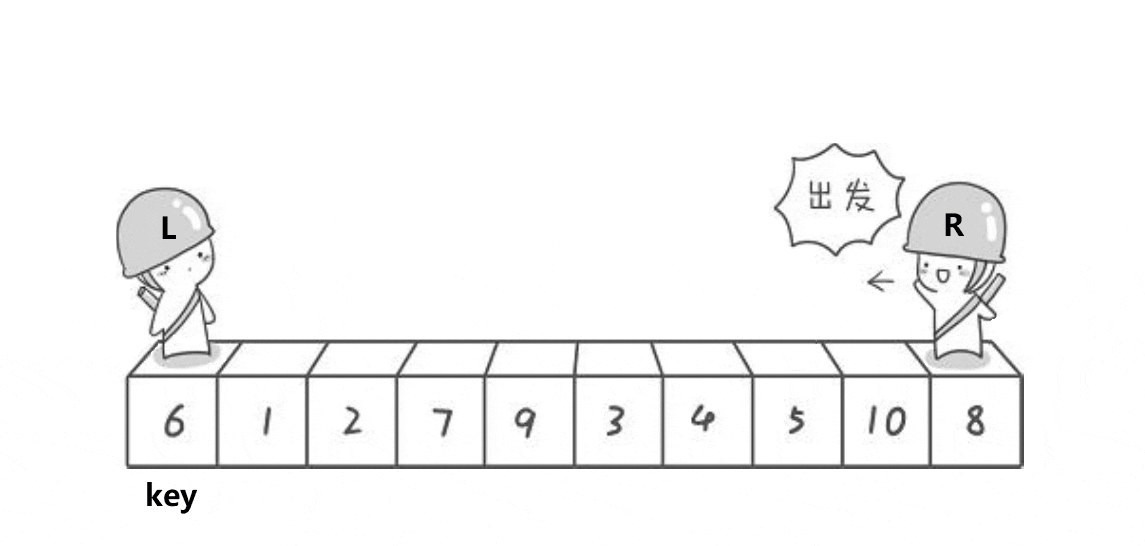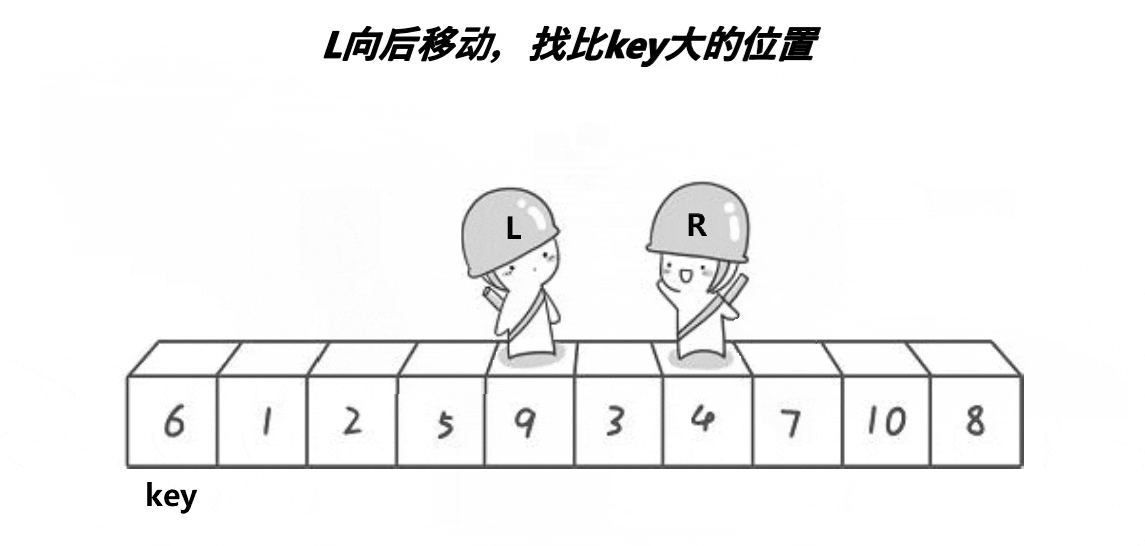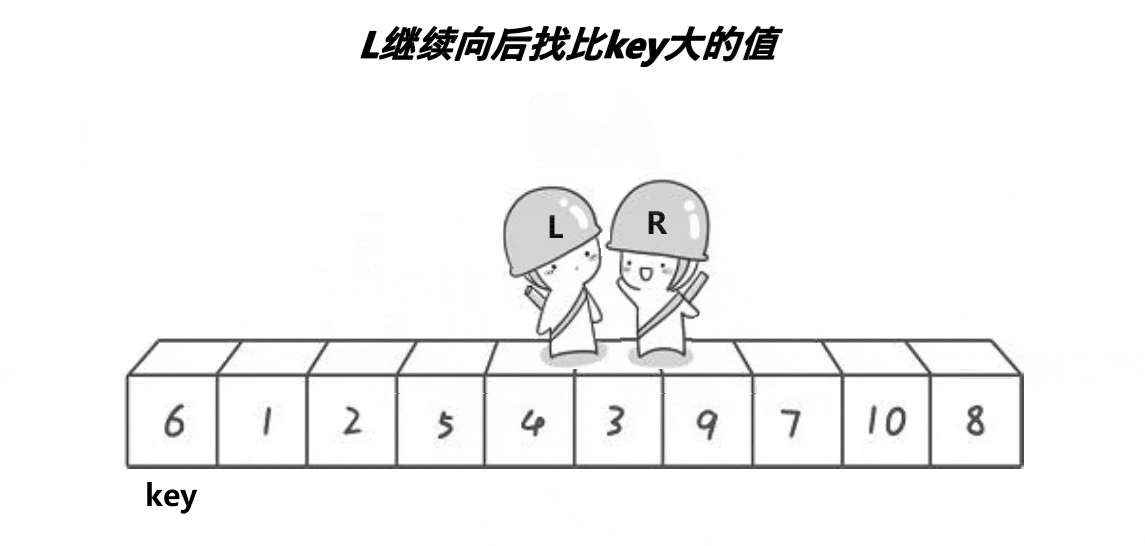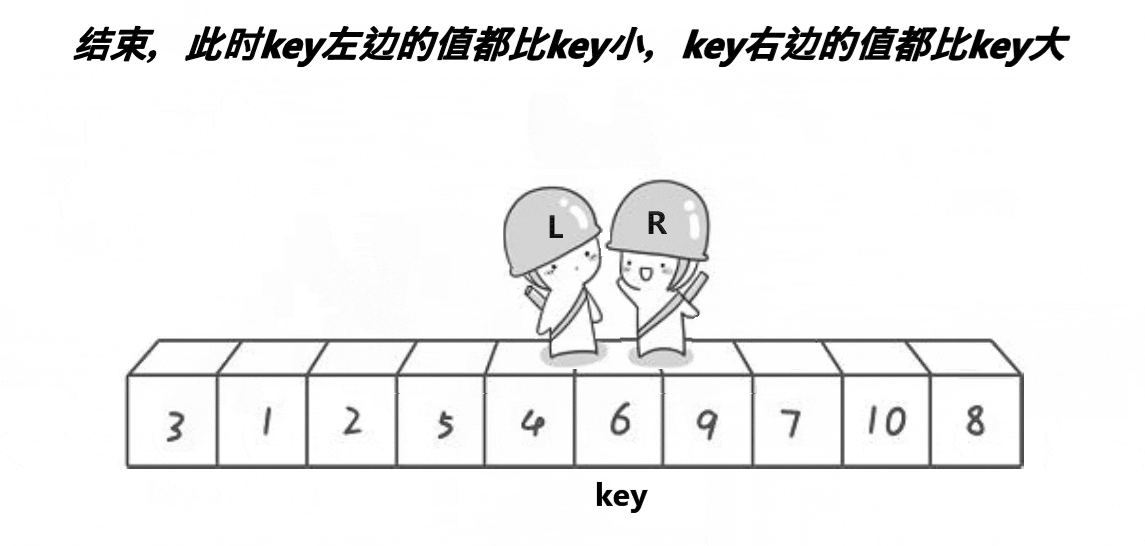
选出一个关键字 key,一般是头或者尾。经过一次单趟后,key 放到了正确的位置,key 左边的值比 key 小,key 右边的值比 key 大。再让 key 的左边区间有序、key 的右边区间有序。
如何保证相遇位置的值小于 key ?
这个算法右边先走可以保证相遇位置小于 key。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// Hoare
int PartSort1(int* a, int begin, int end)
{int left = begin, right = end;int keyi = left;while (left < right){// 右边先走,找小 -- 升序while (left < right && a[right] >= a[keyi]){--right;}// 左边再走,找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);} Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}b.挖坑法
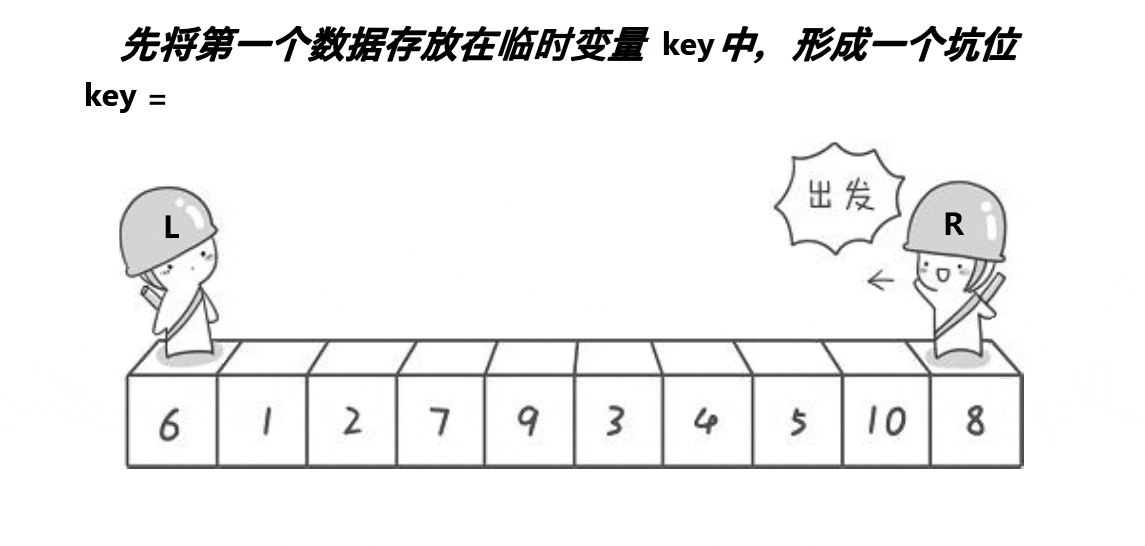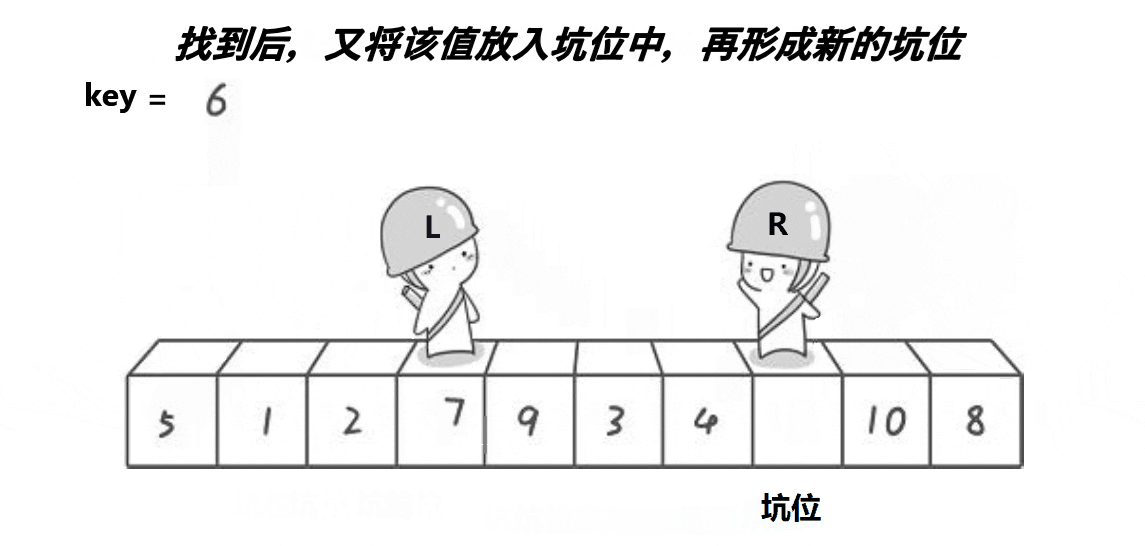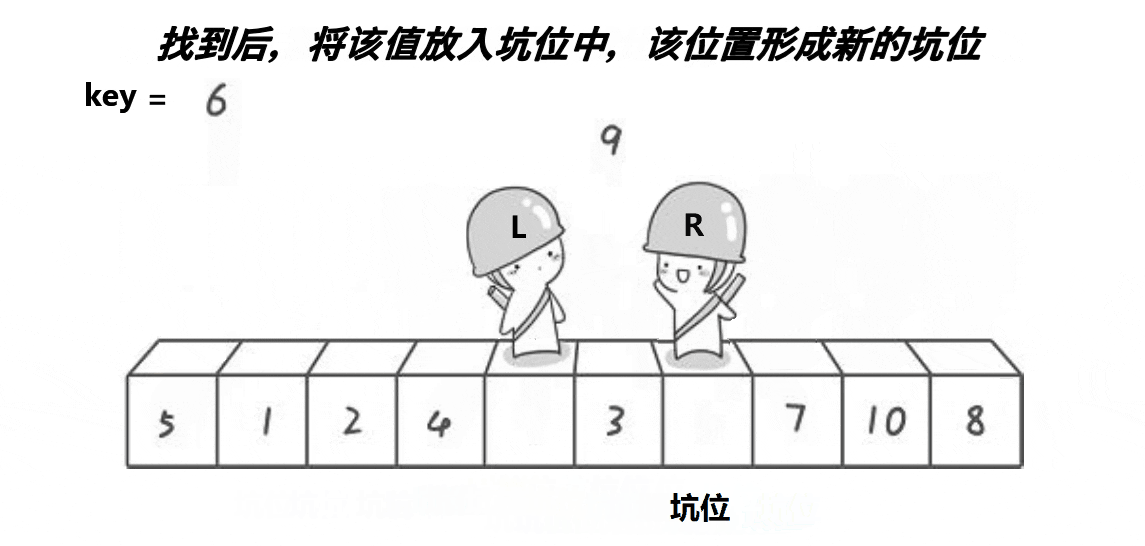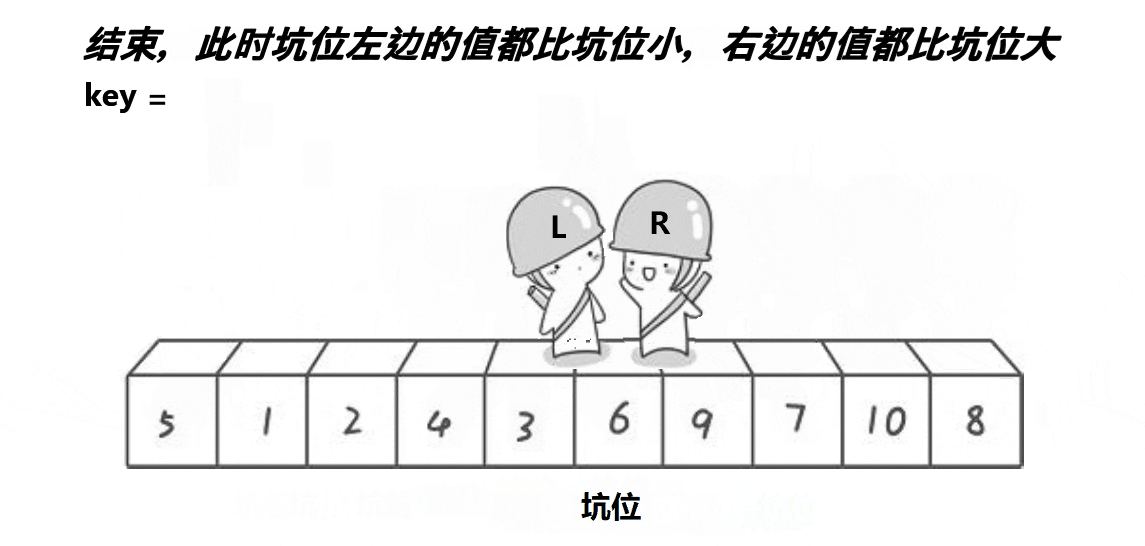
// 挖坑法
int PartSort2(int* a, int begin, int end)
{int key = a[begin];int piti = begin;while (begin < end){// 右边找小,填到左边的坑里面去。这个位置形成新的坑while (begin < end && a[end] >= key){--end;}a[piti] = a[end];piti = end;// 左边找大,填到右边的坑里面去。这个位置形成新的坑while (begin < end && a[begin] <= key){++begin;}a[piti] = a[begin];piti = begin;}a[piti] = key;return piti;
}c.前后指针版本
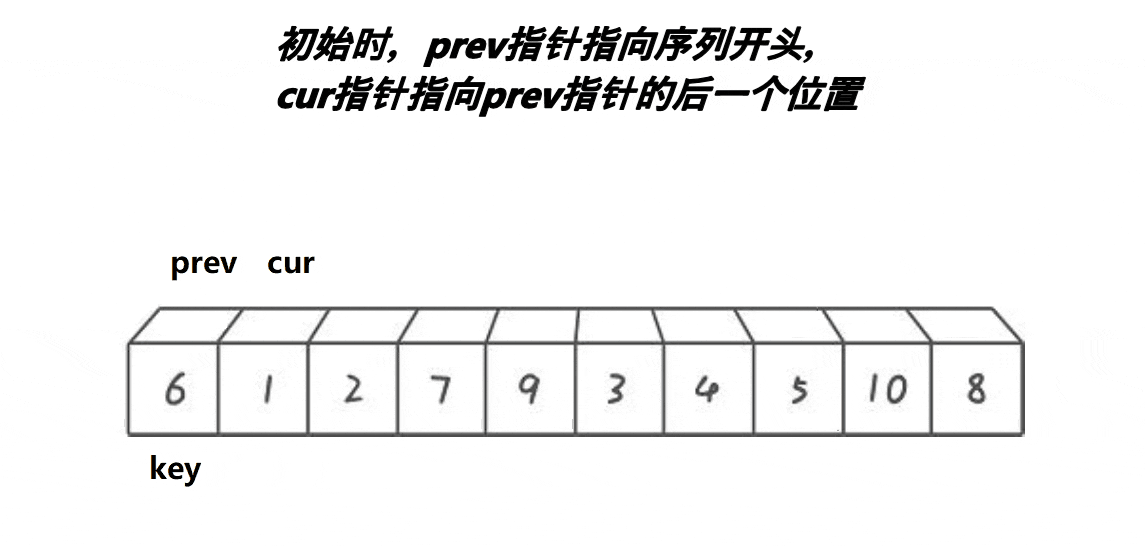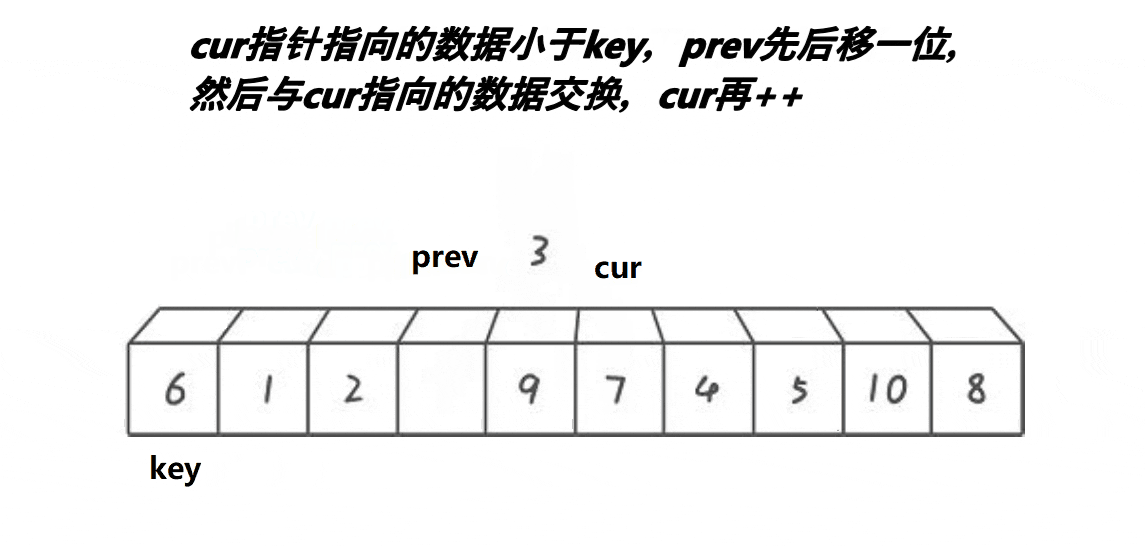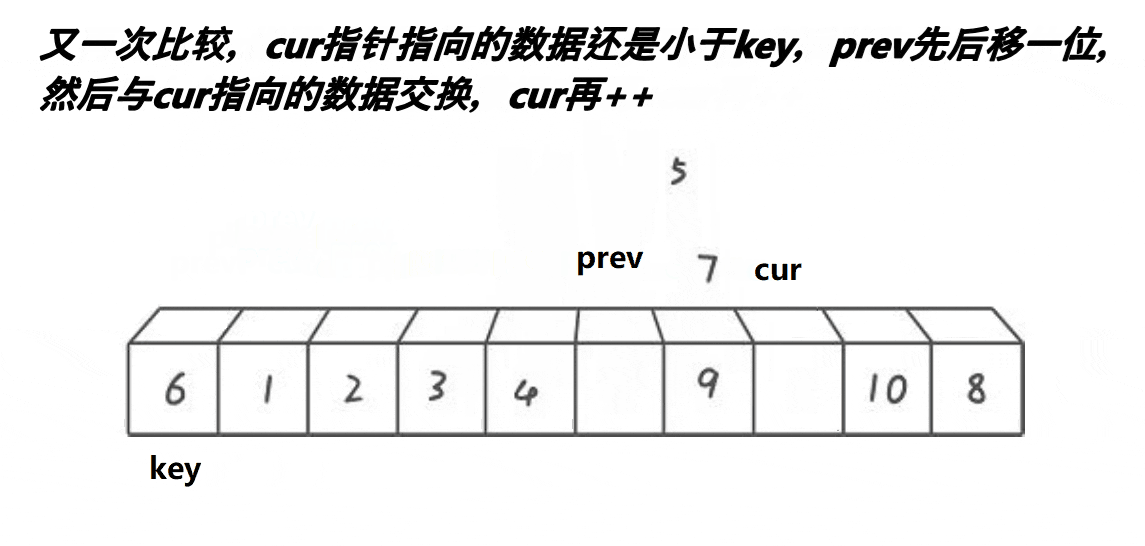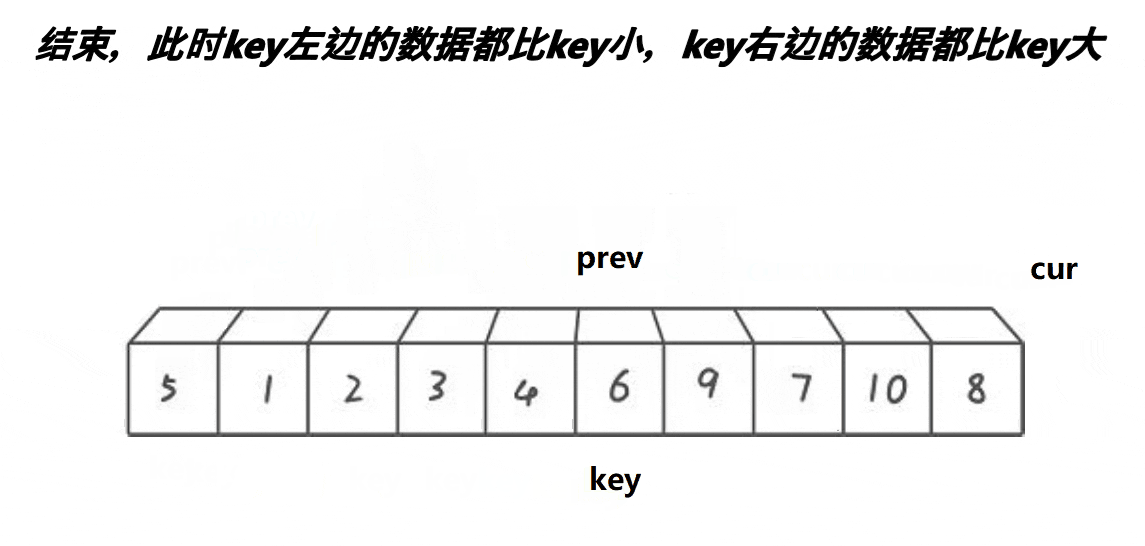
// 前后指针法
int PartSort3(int* a, int begin, int end)
{int prev = begin;int cur = begin + 1;int keyi = begin;// 加入三数取中的优化//int midi = GetMidIndex(a, begin, end);//Swap(&a[keyi], &a[midi]);while (cur <= end){// a[cur]比a[keyi]大时,prev不会++且排除了自己交换自己这种情况if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}(4)快速排序优化 · 三数取中法
- 三数取中法依然无法完全解决针对某种特殊序列(比如元素全部相同)复杂度变为 O(n) 的情况。
- 三数取中法一般选取首、尾和正中三个数进行取中。
- 该方法的基本思想是从待排序数组中随机选择三个元素,并将它们按升序排列。然后,选择中间位置的元素作为 mid 。
这样处理的方式有几个优点,可以提高排序算法的效率:
- 减少最坏情况:选择中间位置的元素,可以避免最坏情况的发生。最坏情况是在每次划分过程中总是选择了最大或最小的元素,导致划分不平衡,使得排序算法的时间复杂度变为 O(n²) 。而三数取中法可以减少最坏情况的发生,提高划分的平衡性。
- 提高划分效率:选择适当的中间元素可以增加划分的平衡性,使得每次划分都能将数组分为近似相等大小的两个部分。这样,在后续的排序过程中,可以减少比较和交换的次数,提高排序算法的效率。
- 三数取中法可以有效地应对一些特殊情况,如数组已经有序或部分有序的情况。在这些情况下,选择中间位置的元素可以避免不必要的划分和比较操作。
- 总的来说,三数取中法通过选择合适的中间元素,可以减少最坏情况的发生,提高划分的平衡性和效率,从而提高排序算法的整体效率。
// 三数取中法
int GetMidIndex(int* a, int begin, int end)
{//int mid = (begin + end) / 2;int mid = left + (right - left) / 2; // 防止溢出版本if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] < a[end]){return end;}else{return begin;}}else // (a[begin] >= a[mid]){if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}
}
- 三数取中法选 key。
- 递归到小的子区间时,可以考虑使用插入排序。
优化后的代码:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// Hoare
int PartSort1(int* a, int begin, int end)
{int left = begin, right = end;int keyi = left;// 加入三数取中的优化int midi = GetMidIndex(a, begin, end);Swap(&a[keyi], &a[midi]);while (left < right){// 右边先走,找小 -- 升序while (left < right && a[right] >= a[keyi]){--right;}// 左边再走,找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);} Swap(&a[keyi], &a[left]);keyi = left;return keyi;
}// 挖坑法
int PartSort2(int* a, int begin, int end)
{int key = a[begin];int piti = begin;// 加入三数取中的优化int midi = GetMidIndex(a, begin, end);Swap(&a[keyi], &a[midi]);while (begin < end){// 右边找小,填到左边的坑里面去。这个位置形成新的坑while (begin < end && a[end] >= key){--end;}a[piti] = a[end]; // 填坑piti = end; // 新坑// 左边找大,填到右边的坑里面去。这个位置形成新的坑while (begin < end && a[begin] <= key){++begin;}a[piti] = a[begin]; // 填坑piti = begin; // 新坑}a[piti] = key; // 将key填到最后一个坑里return piti;
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 前后指针法
int PartSort3(int* a, int begin, int end)
{int prev = begin;int cur = begin + 1;int keyi = begin;// 加入三数取中的优化//int midi = GetMidIndex(a, begin, end);//Swap(&a[keyi], &a[midi]);while (cur <= end){// cur位置的值小于keyi位置的值if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}快速排序是一种高效的排序算法,通常在处理大规模数据时表现良好。然而,当递归到较小区间时,快速排序可能会变得相对较慢。这是因为递归调用本身会带来一定的开销,而对于较小的区间,插入排序可能更加高效。
插入排序是一种简单但有效的排序算法,对于小规模的数据集表现出色。它的时间复杂度为O(n²),但在实际应用中,由于具有低的常数因子和良好的局部性,插入排序通常会比其他 O(n²) 复杂度的排序算法更快。
因此,当快速排序递归到较小区间时,我们可以切换到插入排序。这样可以减少递归调用的次数,降低开销,并且利用插入排序的优势来提高整体性能。
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; ++i){// [0,end]有序,把end+1位置的值插入,保持有序int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]) // 升序{a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = tmp;}
}// 快速排序(递归)
void QuickSort(int* a, int begin, int end)
{// 区间不存在,或者只有一个值则不需要再处理if (begin >= end){return;}if (end - begin > 10){int keyi = PartSort3(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}else // 递归到小的子区间时,可以考虑使用插入排序{InsertSort(a + begin, end - begin + 1);}
}
(5)快速排序非递归
递归的大问题是在极端场景下,如果深度太深,会出现栈溢出。下面用非递归实现快速排序:

- 快速排序的非递归遍历可以使用栈模拟二叉树的前序遍历的方式实现,也可以使用队列模拟二叉树的层序遍历的方式实现。
- 快排的非递归是在模拟递归的过程,所以时间复杂度并没有本质的变化,但是没有递归,可以减少栈空间的开销。
// 快速排序非递归
void QuickSortNonR(int* a, int begin, int end)
{ST st;StackInit(&st);StackPush(&st, end);StackPush(&st, begin);while (!StackEmpty(&st)) // 栈不为空{// 取栈顶left,并Popint left = StackTop(&st);StackPop(&st);// 再取栈顶right,并Popint right = StackTop(&st);StackPop(&st);int keyi = PartSort3(a, left, right); // 这里用前后指针单趟排// [left, keyi-1] keyi [keyi+1, right]if (keyi + 1 < right){StackPush(&st, right);StackPush(&st, keyi + 1);}if (left < keyi - 1) // 至少还有一个以上的值{StackPush(&st, keyi - 1); // 先入右,再入左 -- 先出左,再出右StackPush(&st, left);}}StackDestroy(&st);
}需要入栈的是数组的下标区间,且先入右再入左,因为栈是先进后出,条件是栈不为空。
依次把需要进行单趟排的区间入栈,依次取栈里的区间出来单趟排,再把需要处理的子区间入栈。
快速排序的特性总结:( 前序遍历 )( 层序遍历 )
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序。
- 时间复杂度:O(N*logN)。
- 空间复杂度:O(logN)。
- 稳定性:不稳定。
4、归并排序
(1)基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了 。分治思想跟我们前面讲的递归思想很像。是的,分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧 ,这两者并不冲突。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
(2)归并排序(MergeSort)
归并排序的核心思想还是蛮简单的。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。


void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end){return;}//int mid = (begin + end) / 2;int mid = begin + (end - begin) / 2; // 防止溢出版本// [begin, mid] [mid+1, end] 分治递归,让子区间有序_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// 归并[begin, mid] [mid+1, end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin1;while (begin1 <= end1 && begin2 <= end2) // 其中一个结束就结束{if (a[begin1] <= a[begin2]) // 等于可以保证稳定性{tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}// 将剩余的数字直接填入tmp数组里while (begin1 <= end1) // begin2结束了,拷贝剩下的begin1{tmp[i++] = a[begin1++];}while (begin2 <= end2) //begin1结束了,拷贝剩下的begin2{tmp[i++] = a[begin2++];}// 归并后的结果,拷贝到原数组memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}// 归并排序
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n); // 临时数组if (tmp == NULL){printf("malloc fail\n");exit(-1);}_MergeSort(a, 0, n - 1, tmp); // 子函数递归free(tmp);
}
a.归并排序是稳定的排序算法吗?
在合并的过程中,如果 a[p…q] 和 a[q+1…r] 之间有值相同的元素,先把 a[p…q] 中的元素放入 tmp 数组,这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。
b.归并排序的时间复杂度是多少?
归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(n*logn) 。
c.归并排序的空间复杂度是多少?
归并排序不是原地排序算法。这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。如果我们继续按照分析递归时间复杂度的方法,通过递推公式来求解,那整个归并过程需要 的空间复杂度就是 O(n*logn)。不过,类似分析时间复杂度那样来分析空间复杂度,这个思 路并不对。 实际上,递归代码的空间复杂度并不能像时间复杂度那样累加。刚刚我们忘记了最重要的一 点,那就是,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟 的内存空间就被释放掉了。在任意时刻, CPU 只会有一个函数在执行,也就只会有一个临 时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n) 。
归并排序的特性总结:( 后序遍历 )
- 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)。
- 空间复杂度:O(N)。
- 稳定性:稳定。
(3)归并排序非递归
非递归未必比递归简单,因为这里需要对边界进行精准控制。
// 归并排序(非递归)
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){printf("malloc fail\n");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){// [i, i+gap-1][i+gap, i+2*gap-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// end1越界或者begin2越界,则可以不归并if (end1 >= n || begin2 >= n){break;}else if (end2 >= n) // 修正边界{end2 = n - 1;}int m = end2 - begin1 + 1; //实际归并的总体个数int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1) // begin2结束了,拷贝剩下的begin1{tmp[j++] = a[begin1++];}while (begin2 <= end2) // begin1结束了,拷贝剩下的begin2{tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * m); // 拷贝回原数组}gap *= 2; // 迭代}free(tmp);
}
5、非比较排序
(1)思想
- 计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
(2)计数排序(CountSort)
操作步骤:
- 统计相同元素出现次数。
- 根据统计的结果将序列回收到原来的序列中。

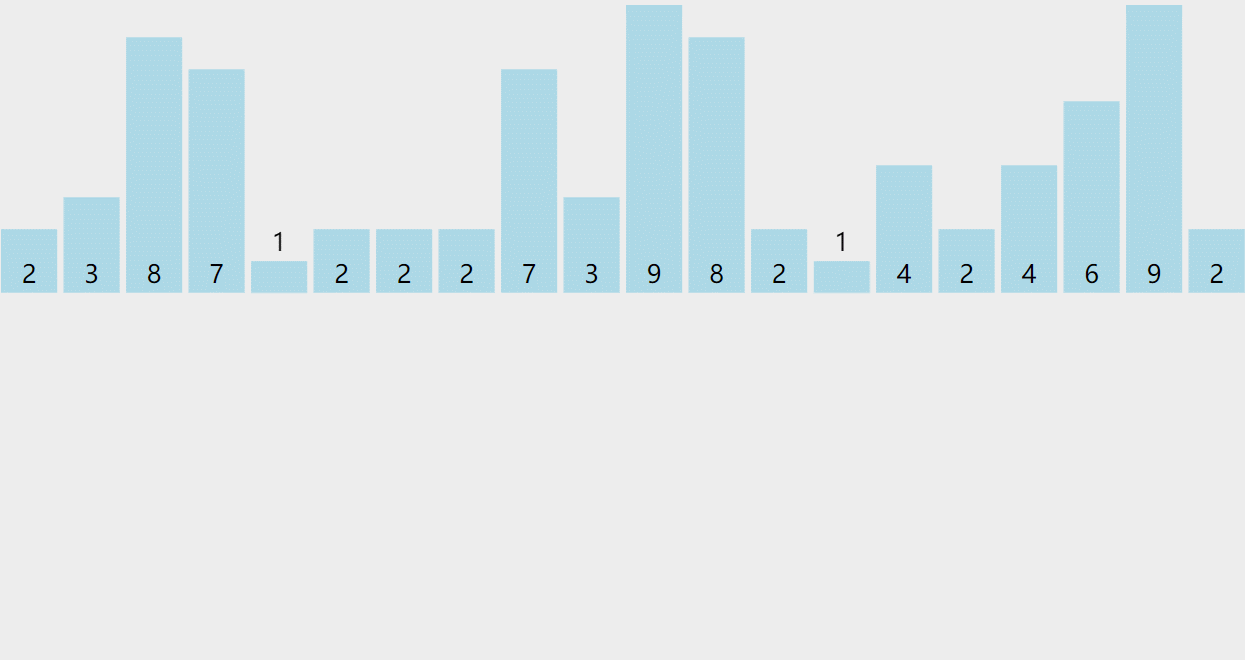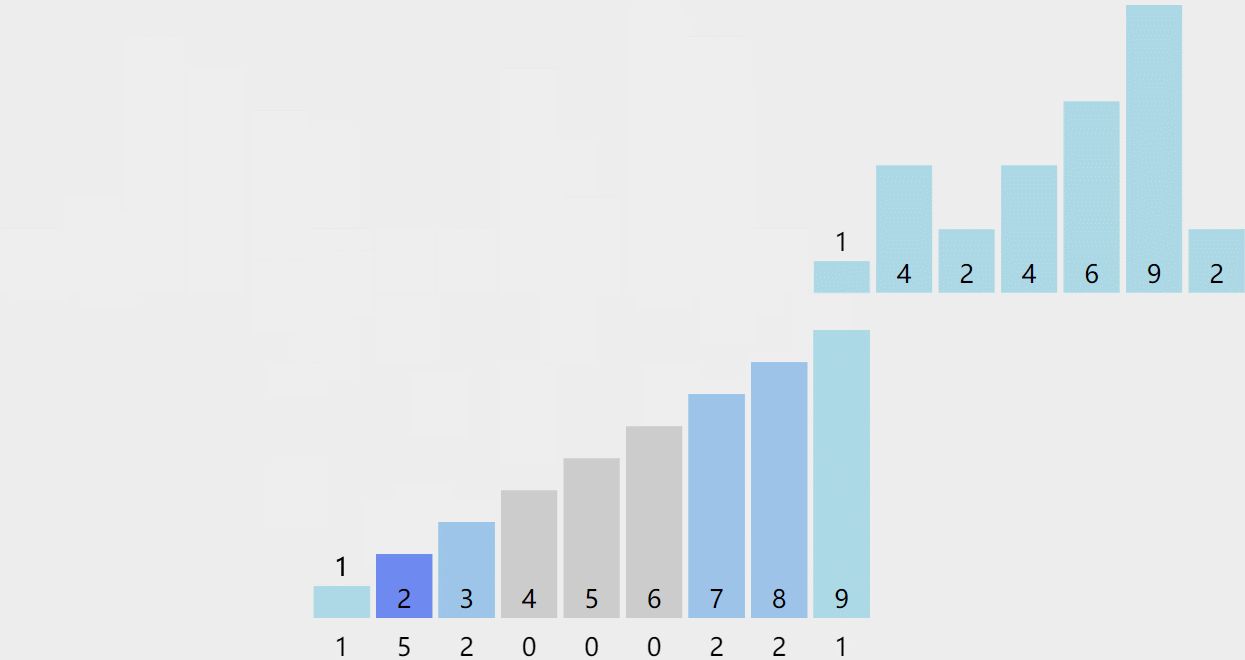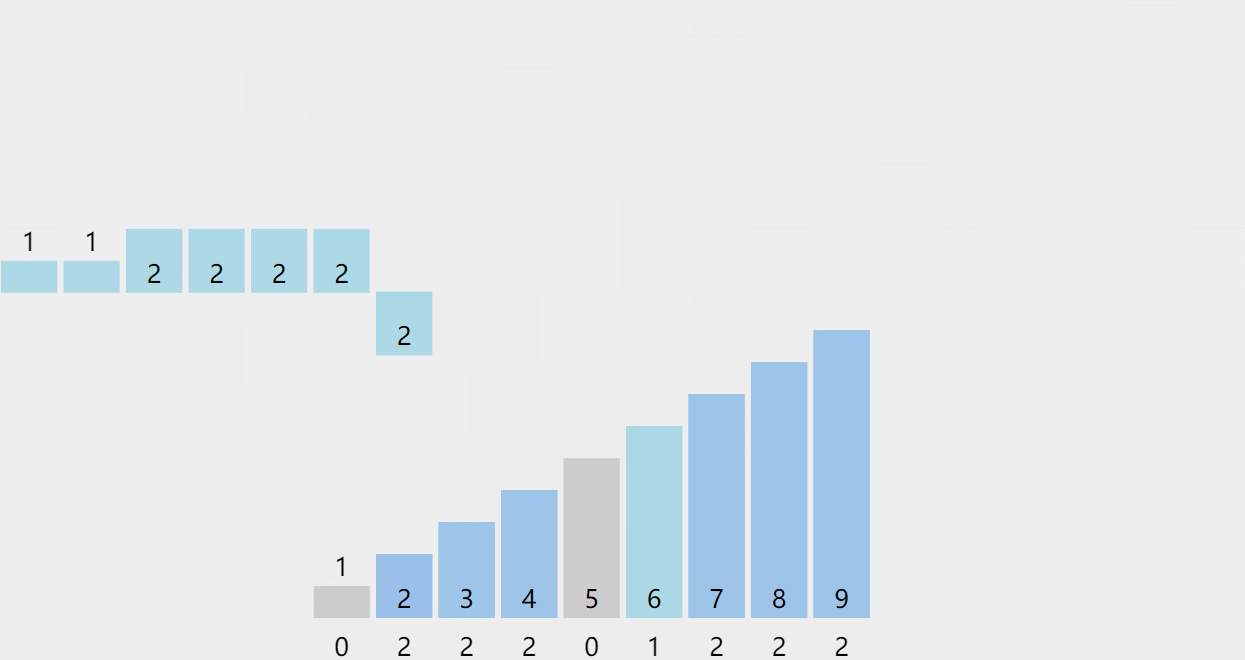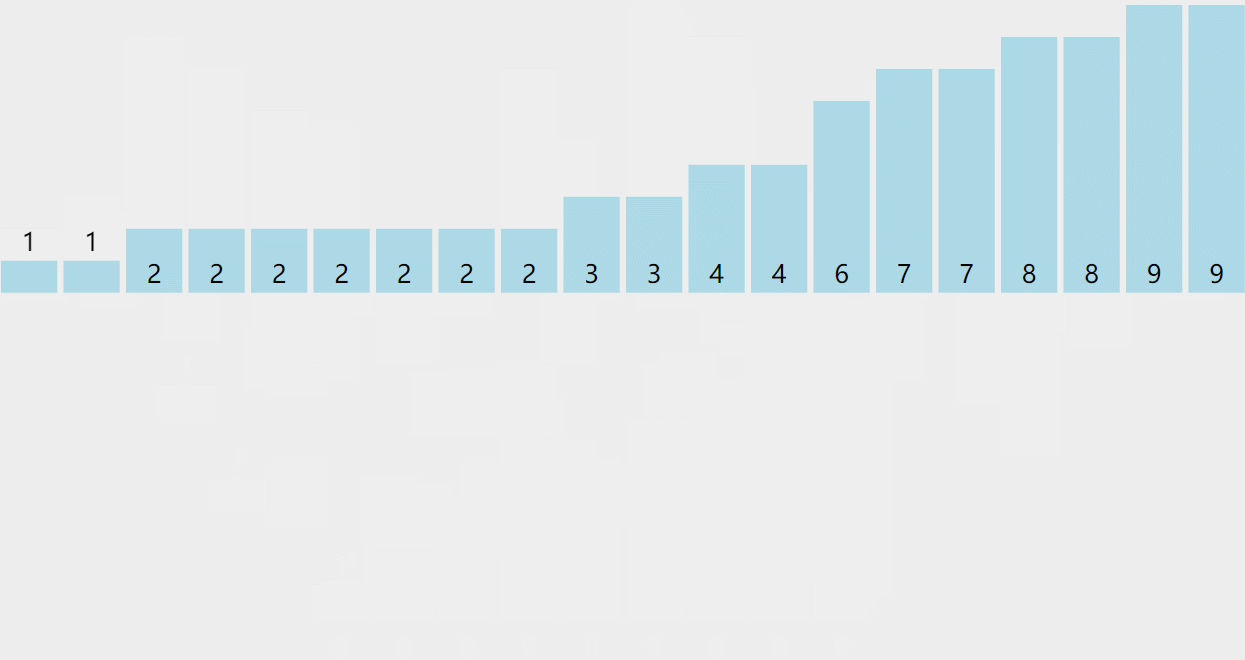
// 计数排序
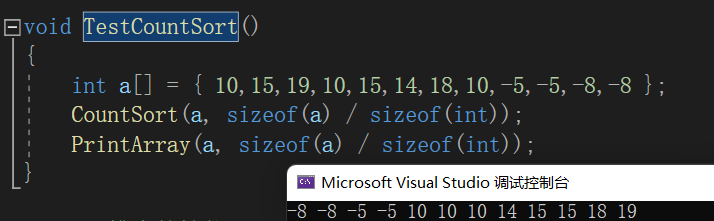
void CountSort(int* a, int n)
{int min = a[0], max = a[0];// 找出最大最小值for (int i = 1; i < n; ++i){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}// 统计次数的数组int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){printf("malloc fail\n");exit(-1);}memset(count, 0, sizeof(int) * range); // 初始化为0//统计次数for (int i = 0; i < n; ++i){count[a[i] - min]++;}//回写-排序int j = 0;for (int i = 0; i < range; ++i){// 出现几次就要回写几个i+minwhile (count[i]--){a[j++] = i + min;}}free(count);
}
- 如果要开 0~5000 个数据的数组,但其实小于 1000 的数据一个都没有,空间浪费严重,这种方式叫作绝对映射。
- 针对此情况,如果我们只需要 0~4000 个数据的数组即可,放数据时是 a[i] - min,这种方式叫作相对映射。
注意 :计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数 据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,range))。
- 空间复杂度:O(range)。
- 稳定性:稳定。
三、排序算法复杂度及稳定性分析
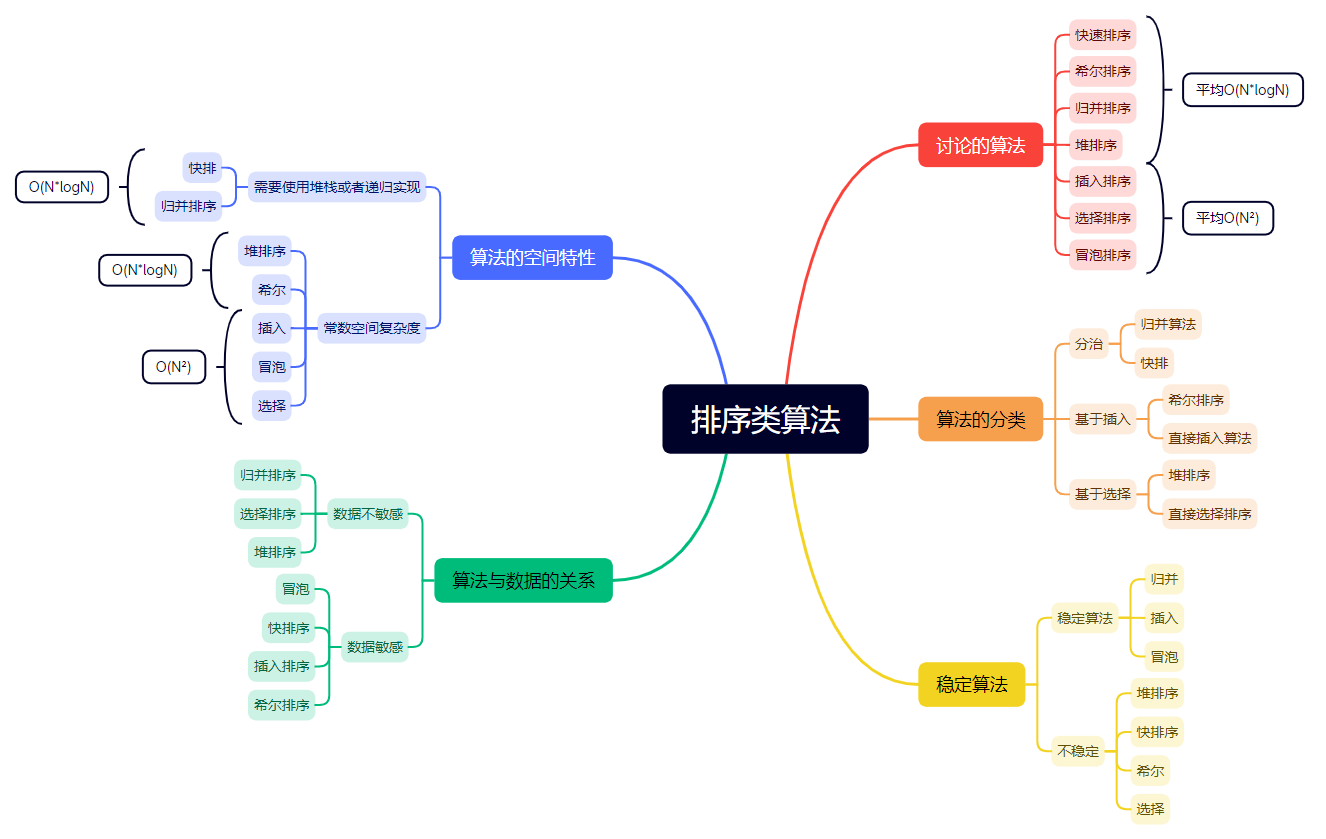

相关文章:

【数据结构】排序(插入、选择、交换、归并) -- 详解
一、排序的概念及其运用 1、排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记…...
游戏中的图片打包流程,免费的png打包plist工具,一款把若干资源图片拼接为一张大图的免费工具
手机游戏开发中,为了提高图片渲染性能,经常需要将小图片合并成一张大图进行渲染。如果手工来做的话就非常耗时。TexturePacker就是一款非常不错方便的处理工具。TexturePacker虽然非常优秀,但不是免费的。 对于打包流程,做游戏的…...

Springboot实现ENC加密
Springboot实现ENC加密 1、导入依赖2、配置加密秘钥(盐)3、获取并配置密文4、重启项目测试5、自定义前缀、后缀6、自定义加密方式 1、导入依赖 关于版本,需要根据spring-boot版本,自行修改 <dependency><groupId>co…...

nginx 托管vue项目配置
server {listen 80;server_name your_domain.com;location / {root /path/to/your/vue/project;index index.html;try_files $uri $uri/ /index.html;} }奇怪的现象,在vue路由中/会跳转到/abc/def,但如果直接输入/abc/def会显示404,添加 try_files $uri…...

Vue3中如何进行封装?—组件之间的传值
用了很久一段时间Vue3Ts了,工作中对一些常用的组件也进行了一些封装,这里对封装的一些方法进行一些简单的总结。 1.props传递 首先在主组件进行定义传值 <template><div>这里是主组件<common :first"first"></common&…...
实训笔记8.25
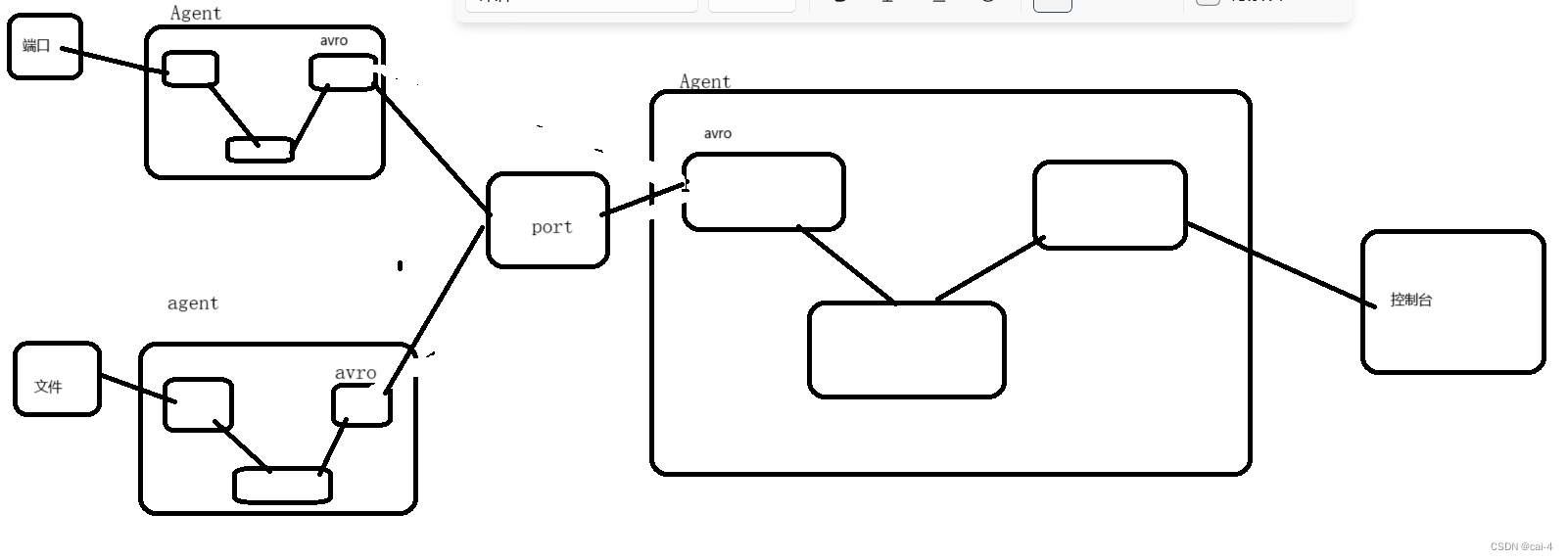
实训笔记8.25 8.25笔记一、Flume数据采集技术1.1 Flume实现数据采集主要借助Flume的组成架构1.2 Flume采集数据的时候,核心是编写Flume的采集脚本xxx.conf1.2.1 脚本文件主要由五部分组成 二、Flume案例实操2.1 采集一个网络端口的数据到控制台2.1.1 分析案例的组件…...

vue自定义监听元素宽高指令
在 main.js 中添加 // 自定义监听元素高度变化指令 const resizerMap new WeakMap() const resizeObserver new ResizeObserver((entries) > {for (const entry of entries) {const handle resizerMap.get(entry.target)if (handle) {handle({width: entry.borderBoxSiz…...

网络爬虫到底是个啥?
网络爬虫到底是个啥? 当涉及到网络爬虫技术时,需要考虑多个方面,从网页获取到最终的数据处理和分析,每个阶段都有不同的算法和策略。以下是这些方面的详细解释: 网页获取(Web Crawling)&#x…...
前端行级元素和块级元素的基本区别
块级元素和行内元素的基本区别是, 行内元素可以与其他行内元素并排;块级元素独占一行,不能与其他任何元素并列; 下面看一下; <!DOCTYPE html> <html> <head> <meta charset"utf-8"&…...

CentOS 7用二进制安装MySQL5.7
[rootlocalhost ~]# [rootlocalhost ~]# ll 总用量 662116 -rw-------. 1 root root 1401 8月 29 19:29 anaconda-ks.cfg -rw-r--r--. 1 root root 678001736 8月 29 19:44 mysql-5.7.40-linux-glibc2.12-x86_64.tar.gz [rootlocalhost ~]# tar xf mysql-5.7.40-linux-…...

华为加速回归Mate 60发布, 7nm全自研工艺芯片
华为于今天12:08推出“HUAWEI Mate 60 Pro先锋计划”,让部分消费者提前体验。在华为商城看到,华为Mate 60 pro手机已上架,售价6999元,提供雅川青、白沙银、南糯紫、雅丹黑四种配色供选择。 据介绍,华为在卫星通信领域…...

Linux系列讲解 —— 【systemd】下载及编译记录
Ubuntu18.04的init程序合并到了systemd中,本篇文章记录一下systemd的下载和编译。 1. 下载systemd源码 (1) 查看systemd版本号,用来确定需要下载的分支 sunsun-pc:~$ systemd --version systemd 237 PAM AUDIT SELINUX IMA APPARMOR SMACK SYSVINIT UT…...
u-view 的u-calendar 组件设置默认日期后,多次点击后,就不滚动到默认日期的位置
场景:uniapp开发微信小程序 vue2 uview版本:2.0.36 ; u-calendar 组件设置默认日期后 我打开弹窗,再关闭弹窗, 重复两次 就不显示默认日期了 在源码中找到这个位置进行打印值,根据出bug前后的值进行…...

vue naive ui 按钮绑定按键
使用vue (naive ui) 绑定Enter 按键 知识点: 按键绑定Button全局挂载使得message,notification, dialog, loadingBar 等NaiveUI 生效UMD方式使用vue 与 naive ui将vue默认的 分隔符大括号 替换 为 [[ ]] <!DOCTYPE html> <html lang"en"> <head>…...
Viobot基本功能使用及介绍
设备拿到手当然是要先试一下效果的,这部分可以参考本专栏的第一篇 Viobot开机指南。 接下来我们就从UI开始熟悉这个产品吧! 1.状态 设备上电会自动运行它的程序,开启了一个服务器,上位机通过连接这个服务器连接到设备,…...

《PMBOK指南》第七版12大原则和8大绩效域
《PMBOK指南》第七版12大原则 原则1:成为勤勉、尊重和关心他人的管家 原则2:营造协作的项目团队环境 原则3:有效地干系人参与 原则4:聚焦于价值 原则5:识别、评估和响应系统交互 原则6:展现领导力行为…...

docker 启动命令
cd /ycw/docker docker build -f DockerFile -t jshepr:1.0 . #前面测试docker已经介绍过该命令下面就不再介绍了 docker images docker run -it -p 7003:9999 --name yyy -d jshepr:1.0 #上面运行报错 用这个 不报错就不用 docker rm yyy docker ps #查看项目日志 docker …...
C++ DAY7
一、类模板 建立一个通用的类,其类中的类型不确定,用一个虚拟类型替代 template<typename T> 类template ----->表示开始创建模板 typename -->表明后面的符号是数据类型,typename 也可以用class代替 T ----->表示数据类型…...

Vue2 使用插件 Volar 报错:<template v-for> key should be placed on the <template> tag.
目录 问题描述 版本描述 问题定位 问题解决 VS Code 插件地址 问题描述 在 VS Code 上使用插件 Volar 开发 Vue3 项目,然后去改 Vue2 项目时,对没有放在<template v-for> 元素上的 :key,会提示 <template v-for> key should…...
和 run ()有什么区别)
启动线程方法 start ()和 run ()有什么区别
在Java中,线程可以通过调用start()方法或者直接调用run()方法来执行。这两种方式有着重要的区别: start() 方法:当你调用线程的start()方法时,它会使线程进入就绪状态,等待系统调度。系统会为该线程分配资源,并在合适的时机执行线程的run()方法。实际上,start()方法会启…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...



