测试圈的网红工具:Jmeter到底难在哪里?!
雨果的公司最近推出了一款在线购物应用,吸引了大量用户。然而随着用户数量的增加,应用的性能开始出现问题。用户抱怨说购物过程中页面加载缓慢,甚至有时候无法完成订单,小欧作为负责人员迫切需要找到解决方案。
在学习JMeter之前,小欧只能通过手动测试来模拟用户购物行为。但是他很快发现这种方法无法满足真实世界的并发访问场景,也没办法准确评估应用的性能承载能力。
当他掌握了JMeter并将其应用于接口 性能测试时之后,一切都变得不同了。他先创建了一场真实的压力测试,使用JMeter模拟了上千个同时访问购物应用的用户,而且设置了各种购物场景(包括浏览商品、加入购物车、结算订单等),通过JMeter的强大功能,他轻松监控了关键性能指标(页面加载时间、响应时间和吞吐量),并且发现了应用在高负载下的性能瓶颈,提供了有针对性的优化建议,最终测试结果和建议被开发团队采纳,并进行了相应的优化措施。

那么作为一名测试人员,你是否也曾经遇到过这些问题:
同样的起点,同样的工作时间,为什么别人接那么多项目,你还是在点点点;为什么别人升职了,而你还在原地踏步?
同样的工作内容,为什么别人下班了,你还在加班?
在现在竞争激烈的职场中,掌握技术才是职业生涯中的开端和保障。出现上述这些问题都源于你技术能力的不足。那么在技术领域上,如何抢占先机呢?
Jmeter作为一款十分热门的工具,在接口功能测试、接口自动化测试、接口性能测试方面都有着广泛的应用。对于想要赢得职场上一席之地的测试人员来说,掌握Jmeter从入门到精通,并运用于实际场景中,完成接口压测是非常重要的
你可能会问,Jmeter接口测试难不难
其实入门不难,但是想做到深入理解、实际场景运用、接口压测,却非常难。很多人只能做到浅尝辄止,似懂非懂的程度,流于表面,缺乏实际运用的经验,这也是目前市场上大多数测试人员的状态。
那么,如何才能轻松掌握Jmeter核心技能,让自己从行业平均水平中脱颖而出呢?首先,找对资料是非常重要的。即使你是纯小白一枚,没有任何基础,也可以轻松掌握Jmeter核心技能。为了帮助更多测试人员实现技术升级,特别准备了一套Jmeter接口测试免费学习资料!
下面是配套学习资料,对于做【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴我走过了最艰难的路程,希望也能帮助到你!

软件测试面试小程序
被百万人刷爆的软件测试题库!!!谁用谁知道!!!全网最全面试刷题小程序,手机就可以刷题,地铁上公交上,卷起来!
涵盖以下这些面试题板块:
1、软件测试基础理论 ,2、web,app,接口功能测试 ,3、网络 ,4、数据库 ,5、linux
6、web,app,接口自动化 ,7、性能测试 ,8、编程基础,9、hr面试题 ,10、开放性测试题,11、安全测试,12、计算机基础
 资料获取方式 :
资料获取方式 :
相关文章:

测试圈的网红工具:Jmeter到底难在哪里?!
雨果的公司最近推出了一款在线购物应用,吸引了大量用户。然而随着用户数量的增加,应用的性能开始出现问题。用户抱怨说购物过程中页面加载缓慢,甚至有时候无法完成订单,小欧作为负责人员迫切需要找到解决方案。 在学习JMeter之前…...
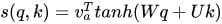
深度学习10:Attention 机制
目录 Attention 的本质是什么 Attention 的3大优点 Attention 的原理 Attention 的 N 种类型 Attention 的本质是什么 Attention(注意力)机制如果浅层的理解,跟他的名字非常匹配。他的核心逻辑就是「从关注全部到关注重点」。 Attention…...
)
简单着色器编写(中下)
这篇我们来介绍另一部分函数。 static unsigned int CreateShader(const std::string& vertexShader, const std::string& fragmentShader) {unsigned int program glCreateProgram();unsigned int vs CompileShader(GL_VERTEX_SHADER,vertexShader);unsigned int f…...
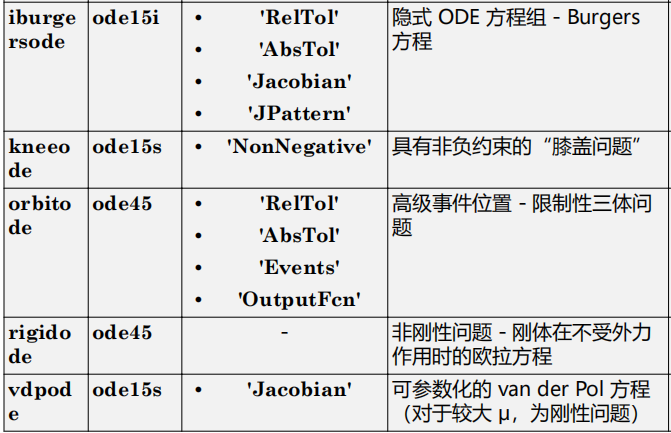
matlab使用教程(24)—常微分方程(ODE)求解器
1.常微分方程 常微分方程 (ODE) 包含与一个自变量 t(通常称为时间)相关的因变量 y 的一个或多个导数。此处用于表示 y 关于 t 的导数的表示法对于一阶导数为 y ′ ,对于二阶导数为 y ′′,依此类推。ODE 的阶数等于 y 在方程中…...

企业级数据共享规模化模式
数据共享正在成为企业数据战略的重要元素。对于公司而言,Amazon Data Exchange 这样的亚马逊云科技服务提供了与其他公司共享增值数据或从这些数据获利的途径。一些企业希望有一个数据共享平台,他们可以在该平台上建立协作和战略方法,在封闭、…...
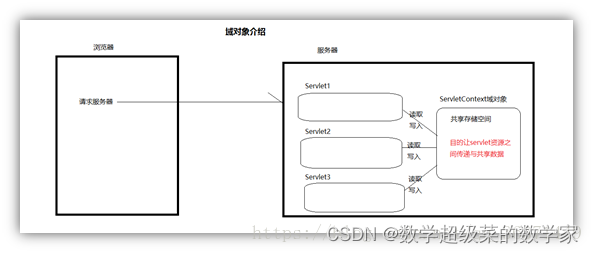
Web服务器-Tomcat详细原理与实现
Tomcat 安装与使用 :MAC 安装配置使用Tomcat - 掘金 安装后本计算机就相当于一台服务器了!!! 方式一:使用本地安装的Tomcat 1、将项目文件移动到Tomcat的webapps目录下。 2、启动Tomcat 3、在浏览器输入想要加载的…...
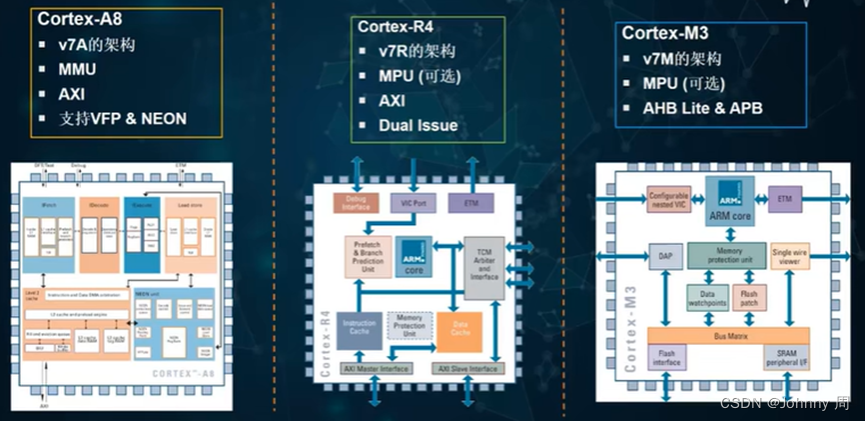
ARM处理器核心概述
一、基于ARM处理器的嵌入式系统 ARM核深度嵌入SOC中,通过JTAG口进行外部调试。计通常既有外部内存又有内部内存,从而支持不通的内存宽度、速度和大小。一般会包含一个中断控制器。可能包含一些Primece外设,需要从ARM公司取得授权。总线使用A…...
万户协同办公平台 ezoffice存在未授权访问漏洞 附POC
文章目录 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC1. 万户协同办公平台 ezoffice简介2.漏洞描述3.影响版本4.fofa查询语句5.漏洞复现6.POC&EXP7.整改意见8.往期回顾 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC 免责声明:请勿利用文章内的相…...
使用ctcloss训练矩阵生成目标字符串
首先我们需要明确 c t c l o s s ctcloss ctcloss是用来做什么的。比如说要生成的目标字符串长度为 l l l,而这个字符串包含 s s s个字符,字符串允许的最大长度为 L L L,这里认为一个位置是一个时间步,就是一拍,记为 T…...
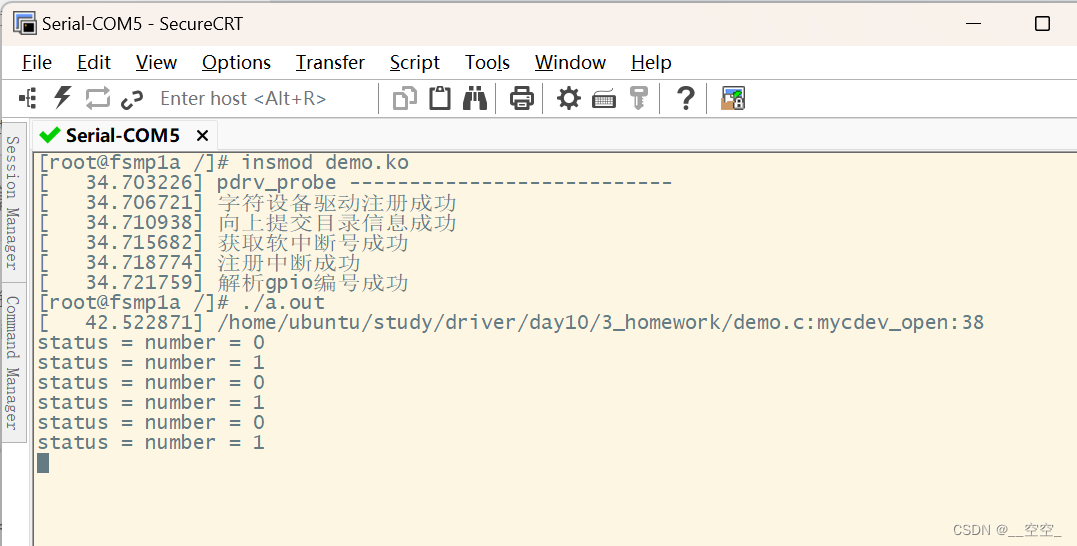
驱动 - 20230829
练习 基于platform实现 在根节点下,增加设备树 myplatform {compatible"hqyj,myplatform";interrupts-extended<&gpiof 9 0>, <&gpiof 7 0>, <&gpiof 8 0>;led1-gpio<&gpioe 10 0>;reg<0x12345678 59>;}…...

数组(个人学习笔记黑马学习)
一维数组 1、定义方式 #include <iostream> using namespace std;int main() {//三种定义方式//1.int arr[5];arr[0] 10;arr[1] 20;arr[2] 30;arr[3] 40;arr[4] 50;//访问数据元素/*cout << arr[0] << endl;cout << arr[1] << endl;cout &l…...

layui表格事件分析实例
在 layui 的表格组件中,区分表头事件和行内事件是通过事件类型(toolbar 和 tool)以及 lay-filter 值来实现的。 我们有一个表格,其中有一个工具栏按钮和操作按钮。我们将使用 layui 的 table 组件来处理这些事件。 HTML 结构&…...

Android NDK JNI与Java的相互调用
一、Jni调用Java代码 jni可以调用java中的方法和java中的成员变量,因此JNIEnv定义了一系列的方法来帮助我们调用java的方法和成员变量。 以上就是jni调用java类的大部分方法,如果是静态的成员变量和静态方法,可以使用***GetStaticMethodID、CallStaticObjectMethod等***。就…...

装备制造企业如何执行精益管理?
导 读 ( 文/ 2358 ) 精益管理是一种以提高效率、降低成本和优化流程为目标的管理方法。装备制造行业具备人工参与度高,产成品价值高,质量要求高的特点。 在装备制造企业中实施精益管理可以帮助企业提高竞争力、提升生产效率并提供高质量的产品。本文将…...

PHP8中自定义函数-PHP8知识详解
1、什么是函数? 函数,在英文中的单词是function,这个词语有功能的意思,也就是说,使用函数就是在编程的过程中,实现一定的功能。即函数就是实现一定功能的一段特定代码。 在前面的教学中,我们已…...

虚拟化技术:云计算发展的核心驱动力
文章目录 虚拟化技术的概念和作用虚拟化技术的优势虚拟化技术对未来发展的影响结论 🎉欢迎来到AIGC人工智能专栏~虚拟化技术:云计算发展的核心驱动力 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客🎈该系…...

光伏+旅游景区
传统化石燃料可开发量逐渐减少,并且对环境造成的危害日益突出。全世界都把目光投向了可再生能源,希望可再生能源能够改变人类的能源结构。丰富的太阳能取之不尽、用之不竭,同时对环境没有影响,光伏发电是近些年来发展最快…...
)
手搓文本向量数据库(自然语言搜索生成模型)
import paddle import jieba import pandas as pd import numpy as np import os from glob import glob from multiprocessing import Process, Manager, freeze_supportfrom tqdm import tqdm# 首先 确定的是输出的时候一定要使用pd.to_pickle() pd.read_pickle() # 计算的时…...

EVO大赛是什么
价格是你所付出的东西,而价值是你得到的东西 EVO大赛是什么? “EVO”大赛全称“Evolution Championship Series”,是北美最高规格格斗游戏比赛,大赛正式更名后已经连续举办12年,是全世界最大规模的格斗游戏赛事。常见…...

linux中使用clash代理
本机环境:ubuntu16 安装代理工具(这里使用clash) 可以手动下载解压,下载地址:https://github.com/Dreamacro/clash 也可以直接使用命令行,演示如下: userlocalhost:~$ curl https://glados.r…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
