2023北京老博会(CBIAIE全国老年产业必参盛会)
CBIAIE北京老博会|把握政策导向,迎合市场需求,引导销售渠道建设,搭建国际化的商业平台;
2023第十届中国(北京)国际老年产业博览会(CBIAIE北京老博会)
The 2023 tenth China (Beijing) International Aged industry Expo
举办时间:2023年08月28-30日
举办展馆:北京亦创国际会展中心
承办单位:北京联诚国际展览有限公司
无限前景:老年产业的发展是社会老龄化的必然结果,老龄化进程持续加速,当前的老年产业已成为我国快速整张的产业之一。我国是世界人口大国,业已进入老龄社会。2021 年末,我国60岁以上老年人口2.78亿,65 岁及以上老年人口超过 2 亿,占总人口 14.2%,老年人口抚养比突破 20%大关。我国总和生育率在 2022 年下探至1.18,已经远低于2.1 的世代更替水平,同时人均预期寿命增长至 78 岁,总人口增速远低于 65 岁以上人口增速,老龄化进程继续加速。根据机构预测,中性场景下到 2030 年,中国 65 岁以上老龄人口将达到 2.58 亿,占总人口 18.23%;到 2050年,中国 65岁以上老龄人口将达到3.95亿,占总人口30.09%,远超美国、日本、德国、英国和法国等发达工业国老龄人口总和,成为拥有世界庞大的老龄群体的国家。
——就全球范围看,近年来,我国老龄人口呈现数大、增速快、高龄化、失能化、空巢化的特点,老龄化程度不断地加深。一方面,老年人生活护理需求与医疗健康需求双重叠加,促使医养健康领域需求旺盛,相关产业发展空间巨大。另一方面,我国医养健康产业尚处在起步阶段,供给侧能力相对不足,存在结构性矛盾和政策性壁垒,优质资源匮乏、医养结合覆盖面窄,专业人员不足,总体难以满足我国老年人不同层次的健康养老服务需求。
——每年定期在我国北京举办的“中国(北京)国际老年产业博览会China (Beijing) International Aged industry Expo”,中英文简称:CBIAIE北京老博会,是我国创展早、规模大、影响力深、市场覆盖广的国际型行业盛会。创展至今,已发展了十二年有余,成功的举办了九届;累计六千余家行业单位和企业参展,两万余款行业产品、技术和服务相继亮相,吸引了超过50万人次的买家前来参观贸易,一千多亿元的成交规模成为了老年行业翘楚,是老年产业发展中的重要环节。
本届展望:2023第十届中国(北京)国际老年产业博览会The 2023 tenth China (Beijing) International Aged industry Expo,定档2023年08月28-30日,在北京亦创国际会展中心再次盛大举办。本届由中国老年保健协会牵头主办,与十余家行业组织联合主办,展览面积超55000平方米,可同时容纳1100家单位、组织和企业参展。届时,将汇聚:中健慈海、日立中国、椿萱茂、燕达养老、优意养老、新华锦、安利智、艾瑞光辉、飞天智能、和颐优年、对桥智能、迈迪加等国内外养老品牌亮相。将吸引来自近两百个国家的70000人次买家参观,力争现场有效的交易达到200亿元。
时间优势:为什么选择在8月下旬举办?是由于老年产业这一特殊行业活动的举办,唯不可缺的是现场要有终端消费者,他们是使用者,一款产品设计是否合理,他们是唯具发言权的群体;必须要让老年人能够安心地去到现场体验产品,与参展的设计者、制造商讲诉需求、提出意见。为了能够让与会的每一位人士安心莅临,组委会通过对三年“口罩”反复爆发数据的研究,我们发现在疫情的这三年里,全年12个月,每年的7月中旬到9月上旬这小两个月的时间里疫情缓和,所以第十届CBIAIE北京老博会特将时间定档8月下旬,为的即是让每一位老年人、行业人士和关注者安心参观,以给参展商的宣传和招商收益提供保障(特别提醒:CBIAIE北京老博会开展期间,8月28/29日仅面向专业买家开放,8月30日面向所有人士开放)。
承办单位:北京联诚国际展览有限公司
Beijing Liancheng International Exhibition Co., Ltd.
相关文章:
)
2023北京老博会(CBIAIE全国老年产业必参盛会)
CBIAIE北京老博会|把握政策导向,迎合市场需求,引导销售渠道建设,搭建国际化的商业平台; 2023第十届中国(北京)国际老年产业博览会(CBIAIE北京老博会) The 2023 tenth China (Beijin…...

【字典转模型 Objective-C语言】
一、点按钮,弹出的这个效果,这实际上是个Label, 这实际上是一个Label,点按钮弹出的这个效果, 设置一个Label的背景色、前景色、透明度、等等, 让它加进来,然后通过动画让它隐藏掉, 这就是,这个效果的实现思路, 咱们这个效果,先稍微往后放一放, 这个并不是重点…...
【LeetCode】剑指 Offer(6)
目录 写在前面: 题目:剑指 Offer 12. 矩阵中的路径 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 写在前面ÿ…...

论文投稿指南——中文核心期刊推荐(法律)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...

Qt音视频开发15-动态切换解码内核的设计
一、前言 动态切换解码内核这个需求也是源自客户的真实需求,既然是动态切换,那肯定是运行期间切换,而不是通过改变标志位重新编译程序来切换,最开始做的就是这种方式,这样就是实现起来简单,但是用起来不够…...

concurrent-map 和 sync.Map,我该选择哪个?
官方的map并不是线程安全的,如果我们在多线程中并发对一个map进行读写操作,是会引发panic的。解决方案除了使用锁来对map进行保护外,还有两种方式:一,开源项目 concurrent-map 提供了可以用来做并发安全的map二&#x…...

华为OD机试 - 最少数量线段覆盖| 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...

【蓝桥集训】第五天——递推
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.砖块递推算法是一种简单的算法,通过已知条件,利用特定关系得出中间推论,逐步递推&…...

qnx的网络知识记录
1、网络驱动加载http://www.qnx.com/developers/docs/7.1/index.html#com.qnx.doc.core_networking/topic/drivers_Loading.html使用mount挂载io-pkt模块mount -Tio-pkt /lib/dll/devnp-e1000.sonicinfo 命令可以查看网卡的各种状态,包括phy的状态2、iopktiopkt的介…...

【Vue/基础知识】Vue基础知识(一)
如果觉得我的分享有一定帮助,欢迎关注我的微信公众号 “码农的科研笔记”,了解更多我的算法和代码学习总结记录。或者点击链接扫码关注 【Vue/基础知识】Vue基础知识(一) 1、v-show 和 v-if 指令的共同点和不同点? 共…...
Iceberg实战踩坑指南
第 1 章 介绍 Apache Iceberg 是一种用于大型分析数据集的开放表格,Iceberge 向 Trino 和 Spark 添加了使用高性能格式的表,就像 Sql 表一样。 Iceberg 为了避免出现不变要的一些意外,表结构和组织并不会实际删除,用户也不需要特…...

预告|2月25日 第四届OpenI/O 启智开发者大会昇腾人工智能应用专场邀您共启数字未来!
如今,人工智能早已脱离科幻小说中的虚构想象,成为可触及的现实,并渗透到我们的生活。随着人工智能的发展,我们正在迎来一个全新的时代——数智化时代。数据、信息和知识是这个时代的核心资源,而人工智能则是这些资源的…...
UnRaid虚拟机安装OpenWrt软路由
文章目录0、前言1、Openwrt虚拟机安装1.1、前提,需要先在UnRaid中开启虚拟机:1.2、下载OpenWrt虚拟机镜像并上传至UnRaid共享文件夹1.3、创建OpenWrt虚拟机2、开启并设置OpenWrt虚拟机2.1、修改OpenWrt管理ip2.2、OpenWrt的上网设置0、前言 最近折腾了很…...
开发日记-lombok
开发日记-lombok环境问题解决方案:1 Data注解失效 无法正常生成 get和set方法2 RequiredArgsConstructor(onConstructor _(Lazy)) 符号_无法识别环境 idea2020.1lombok1.18.24jdk1.8 问题 Data注解失效 无法正常生成 get和set方法RequiredArgsConstructor(onCons…...

Web3中文|2023年zk赛道爆发,即将推出的Polygon zkEVM有多重要?
2月15日,以太坊第2层解决方案提供商Polygon终于公布了备受期待的扩展更新,其零知识以太坊虚拟机(zkEVM)主网的测试版定于3月27日发布。 据官方消息报道,自去年10月上线测试网以来,已取得许多重要的里程碑&…...
【自然语言处理】主题建模:Top2Vec(理论篇)
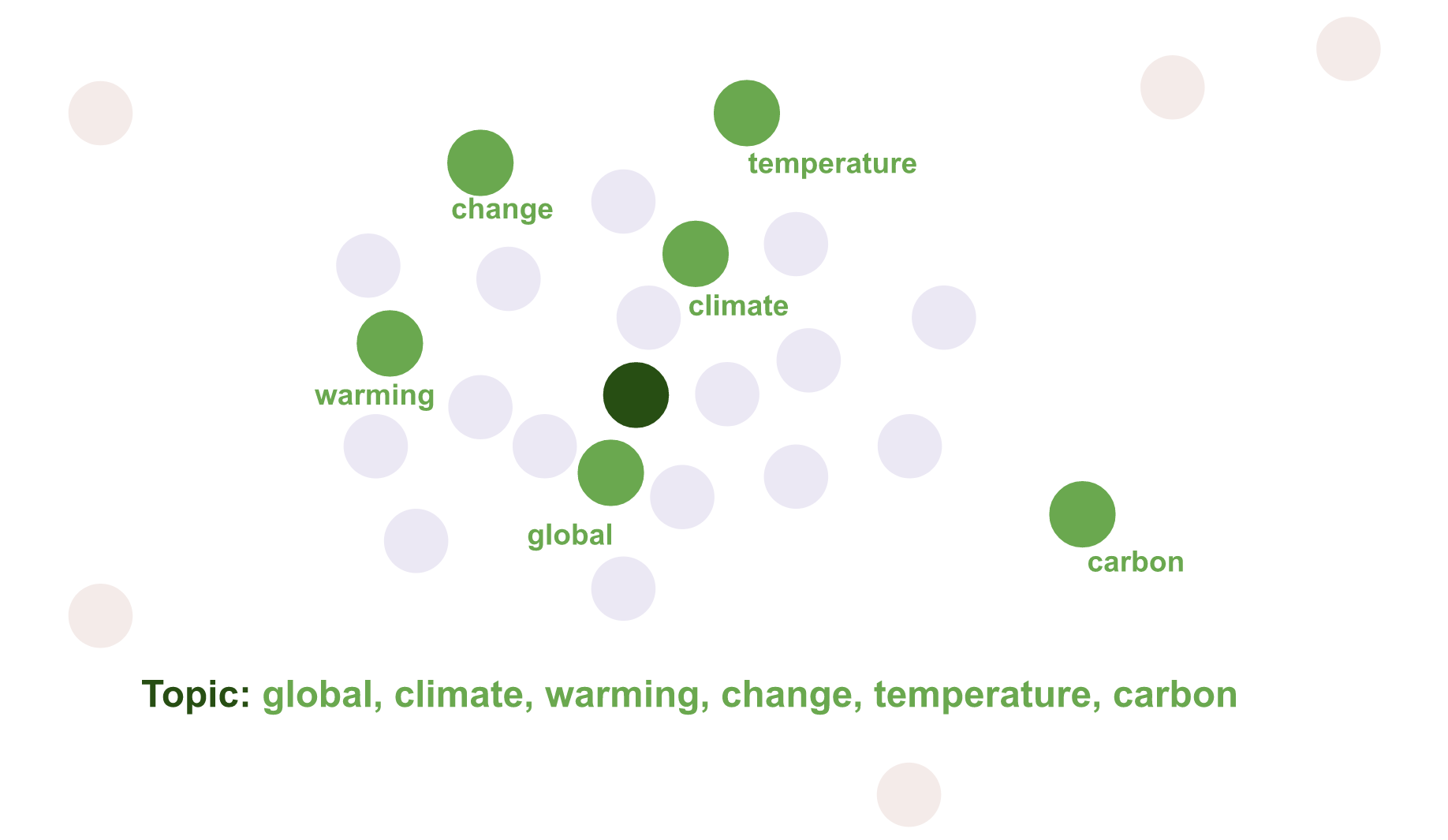
主题建模:Top2Vec(理论篇)Top2Vec 是一种用于 主题建模 和 语义搜索 的算法。它自动检测文本中出现的主题,并生成联合嵌入的主题、文档和词向量。 算法基于的假设:许多语义相似的文档都可以由一个潜在的主题表示。首先…...

【ICLR 2022】重新思考点云中的网络设计和局部几何:一个简单的残差MLP框架
文章目录RETHINKING NETWORK DESIGN AND LOCAL GEOMETRY IN POINT CLOUD: A SIMPLE RESIDUAL MLP FRAMEWORKPointMLP残差点模块几何仿射模块精简版模型:PointMLP-elite实验结果消融实验RETHINKING NETWORK DESIGN AND LOCAL GEOMETRY IN POINT CLOUD: A SIMPLE RESI…...
 原理)
《MySQL学习》 count(*) 原理
一 . count(*)的实现方式 MyISAM 引擎把一个表的总行数存在了磁盘上,因此执行 count() 的时候会直接返回这个数,效率很高; 而 InnoDB 引擎就麻烦了,它执行 count(*) 的时候,需要把数据一行一行…...
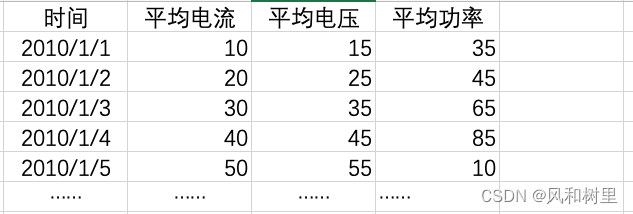
时间序列数据预测的类型
本文主要内容是使用LSTM网络进行不同类型的时间序列预测任务,不涉及代码,仅仅就不同类型的预测任务和数据划分进行说明。 参考文章:https://machinelearningmastery.com/how-to-develop-lstm-models-for-time-series-forecasting/ 注…...

sk_buff结构体成员变量说明
一. 前言 Socket Buffer的数据包在穿越内核空间的TCP/IP协议栈过程中,数据内容不会被修改,只是数据包缓冲区中的协议头信息发生变化。大量操作都是围绕sk_buff结构体来进行的。 sk_buff结构的成员大致分为3类:结构管理域,常规数据…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
