MATLAB实现AHP层次分析法——以情人节选取礼物为例
问题背景:
情人节来临之际,广大直男(女)同胞在给异性朋友选购礼物时会遇到难题——什么才是礼物好坏最重要的标准?基于层次分析法AHP进行计算,得出最高权重的指标,给出各位朋友选购礼物的一种思路,指导大家选到更为贴切的礼物。
使用模型:
AHP层次分析法
反思与总结
- AHP算法的主观性还是很强,虽然较直男的主观臆断来说相对好些,但在构造判断矩阵时的主观臆断很难规避。
- 另外,对于性别、职业等问题,AHP的局限性更加明显。
- 解决方法,就是在大量的调查数据中取平均,构造尽可能客观的判断矩阵。
目录
一.指标确定(建立准则层)
二.权值确定:
三.举例验证(建立方案层)
四.AHP的理论知识
五.MATLAB代码实现
一.指标确定(建立准则层)
(1)问题分析
学生党在给自己的couple挑选礼物时,需要考虑哪些主要方面?根据知乎、b站、抖音等自媒体平台和知网上面的相关文献,得出以下几个比较主要的考虑指标:
- 实用性
- 纪念价值(心意):
- 价位
- 外观
- 主权(“有个人身份的象征标志:如戒指上面刻字”):
- 他(她)的喜好
…………等
为了便于统计分析,选取其中“心意、价位、实用性、喜好”四项作为本次分析的指标。
接下来我们将计算各种指标的权值,具体有如下三种方式:
- 笔者角度:作为0.5倍的直男,对指标进行打分
- 统计分析:分别统计100+个男生、女生对权重的打分,取平均值
- 进行层次分析法思想:实现分而治之,对各种指标两两比较,理性计算权值
如上三种统计方式中:
- 对于男性,按照0.1、0.1,0.8的权重再取各自的加权,计算最终指标的权重。
- 对于女性,由于笔者是男性,出于减少主观性的角度考虑,第一项和第三项均无法计算,直接按照第二项——问卷取平均分即可。
(2)对于男性:
1.笔者自己赋予的权重:
根据笔者的直男思想,赋予如下表中的权值:
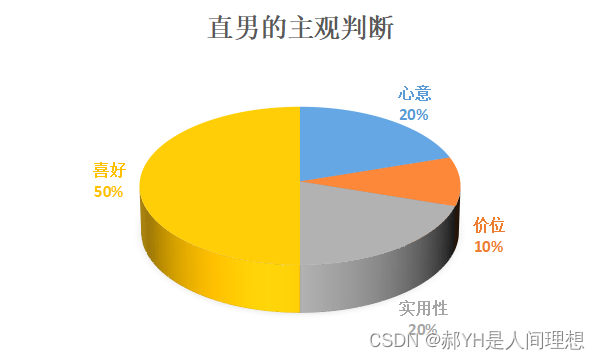
2.统计分析13位男生:
由于调查方式有限,本次调查仅获取到13位男生的想法,为了保证结果的严谨性,首先对异常值进行剔除,最后有11名男生的数据认为真实有效,并使用算术平均计算各项的均分,结果经可视化处理后如下:
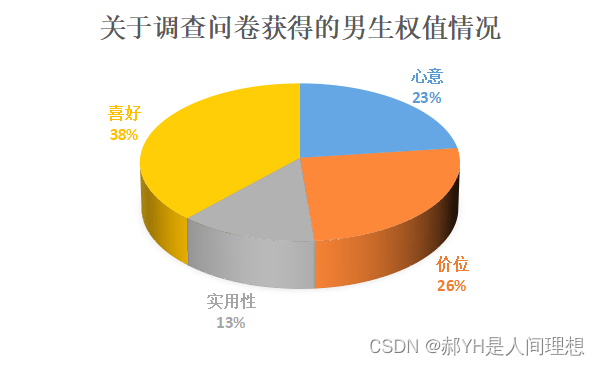
3.层次分析法思想:
- 原理:
如果一次性考虑全部四个指标,往往会考虑不周;如果我们采取分而治之的思想,两两比较,最终根据结果推算权重,相比之下会周到很多。
- 局限性:
出于笔者自身角度考虑,故赋予权值时主观性仍然很强。
(优化方法:调查问卷取平均,不过该方法比较专业化,面向大众调查时统计数据由一定的难度)。
4.具体实现步骤:
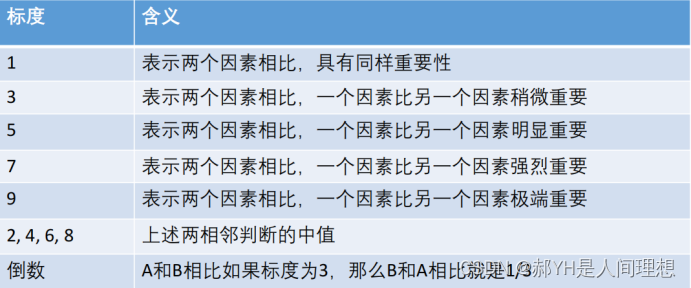
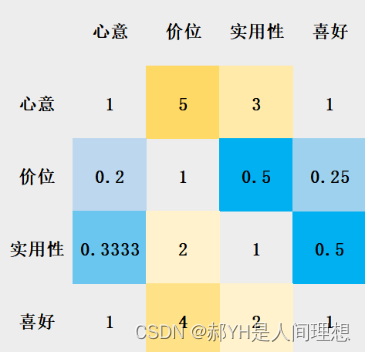
- 首先,给出两两比较的重要程度表:
- 进行判断:根据组合数原理C(4,2),一共需要比较6次。
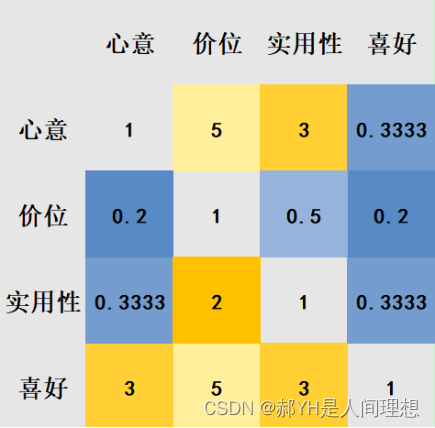
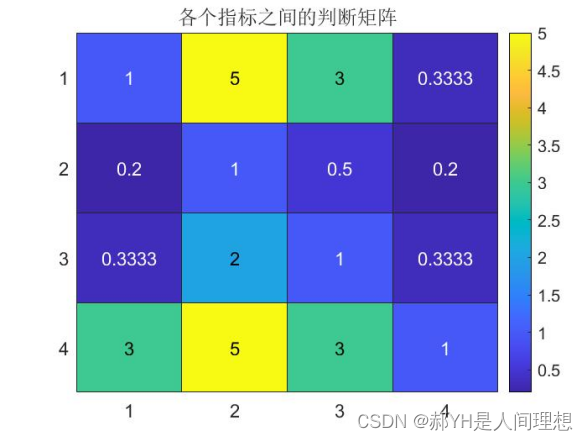
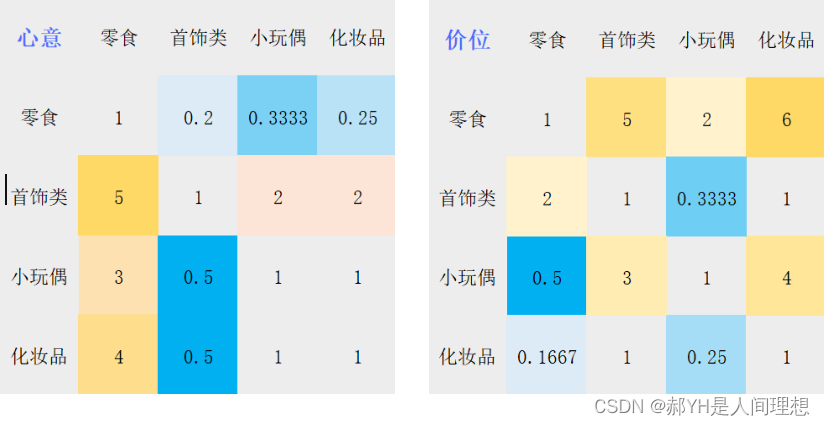
如下图:黄色越深代表越重要,蓝色越深代表越不重要
上图得到的结果,即为层次分析法中的判断矩阵。
- 判断矩阵的一致性检验
在层次分析法的判断矩阵中,可能会出现这样的问题:不一致现象。
我们做出如下假设:A代表心意,B代表价位,C代表实用性。
在矩阵中的(2,1)号元素,我们发现,A之于B的重要程度为5——即心意远大于价位这件事是正确的。假设此时(3,1)号元素的值也为1,则有A=C成立——即心意和实用性一样重要。但当我们观察(2,3)号元素,会发现:实用性之于价位的重要程度为2,与心意之于价位的重要程度是不相同的,我们把这样的矛盾称为不一致现象。
在层次分析法中有如下的定义,若判断矩阵为完全一致矩阵,则必有(m,n)的元素与(n,k)的元素相乘的结果与(m,k)中的元素值相等。
且很容易得出结论:一致矩阵的行和列之间是成倍数关系的。
在层次分析法中,的要求各指标形成的判断矩阵必须一致,才可以进一步计算各指标的权值。然而,结合实际问题与主观因素的影响,构造绝对的一致性矩阵往往是不现实的。
因此我们采用一致性检验。所谓一致性检验,就是检查真实构造出的判断矩阵和一致性矩阵是否有较大差距。原理大致如下,这里不予证明。
使用MATLAB计算本文中判断矩阵的最大特征值,结果为4.1580,代码段在附录之中。
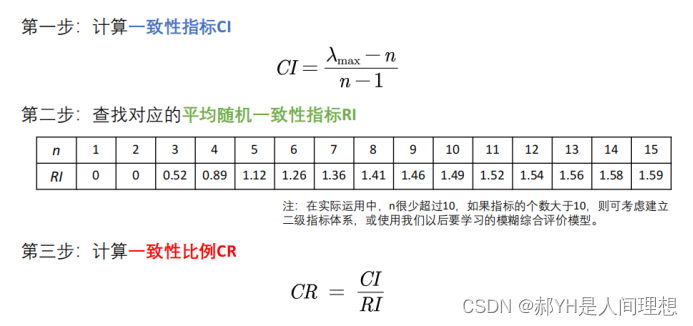
接下来开始一致性检验,步骤不再赘述,大致如下:
经计算,CR的值为0.5918,因为CR>0.1,所以上述判断矩阵未经过一致性检验,需要对判断矩阵进行修正!上述情况也一定程度体现出了AHP方法的局限性。
后经过6次修改,得到崭新的判断矩阵,如下图。
上述判断矩阵的一致性比例是0.0598<0.1,故我们可以认为其满足一致性检验,且上述矩阵为真正使用的矩阵。
- 计算各项指标的权值
在满足一致性检验之后,即可对判断矩阵进行加权的计算。在计算加权时,我们有三种计算方法,分别是算术平均法、几何平均法以及特征值法,为了保证结果的严谨性,此处的三种计算方式将全部使用。此外,无论哪种计算权重的方法,在计算前先要对判断矩阵进行归一化处理。
经MATLAB计算,归一化处理的矩阵为上图。
接下来分别使用三种方式计算4项指标各自的权重:
算术平均法:
根据MATLAB软件,计算得权重为以下值:
指标
权值
心意
0.4091
价位
0.0825
实用性
0.1585
喜好
0.3499
几何平均法:
根据MATLAB软件,计算得权重为以下值:
指标
权值
心意
0.4094
价位
0.0827
实用性
0.1581
喜好
0.3498
特征值法:
根据MATLAB软件,计算得权重为以下值:
指标
权值
心意
0.4098
价位
0.0824
实用性
0.1579
喜好
0.3499
综上所述,三种方式求得的指标权值如下表所示:
指标
算术平均法
几何平均法
特征值法
心意
0.4091
0.4094
0.4098
价位
0.0825
0.0827
0.0824
实用性
0.1585
0.1581
0.1579
喜好
0.3499
0.3498
0.3499
从上表可以看出,三种方法求得的权值近乎相同,这与一致性指标较小——即矩阵一致性较强有关。这里我们采用进一步的算术平均法,为三种方式赋予相同的权重,计算最后的指标权重,如下图:
指标
AHP法权值
心意
0.4094
价位
0.0825
实用性
0.1582
喜好
0.3499
总和
1.0000
上表即为层次分析法APH所求得的指标权值。
(3)对于女生
由于笔者是男生,所以无法通过方法一及方法三计算权值,只能通过搜集问卷来统计分析。
问卷中调查了120位给出的结果,在去除异常值后,得到如下的权值分布(此处的饼图按照整数制作,具体数值在之后会给出):
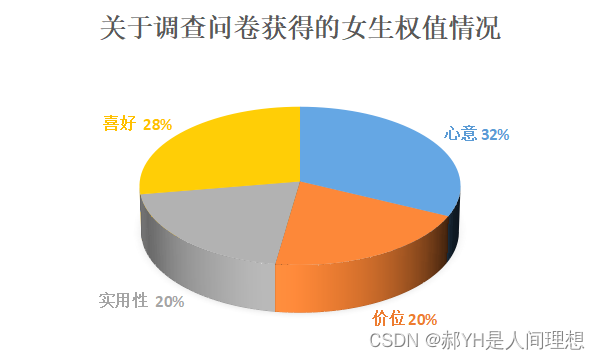
二.权值确定:
对于男生,三种方式的计算结果分别如下:
| 指标 | 直男主观臆断 | 调查统计 | 层次分析法AHP |
| 心意 | 0.5 | 0.38 | 0.4094 |
| 价位 | 0.1 | 0.26 | 0.0825 |
| 实用性 | 0.15 | 0.13 | 0.1582 |
| 喜好 | 0.25 | 0.23 | 0.3499 |
| 权值 | 0.1 | 0.1 | 0.8 |
则最终得到的男生选礼物时的权重为:
| 指标 | 最终权值 |
| 心意 | 0.4035 |
| 价位 | 0.1028 |
| 实用性 | 0.1545 |
| 喜好 | 0.3402 |
对于女生,直接按照统计结果,即可得出各项指标的权重。
| 指标 | 最终权值 |
| 心意 | 0.3208 |
| 价位 | 0.2025 |
| 实用性 | 0.2009 |
| 喜好 | 0.2758 |
三.举例验证(建立方案层)
在问卷中,笔者还调查了两性在送另一半礼物时典型的几种选择,归纳整理后,大致如下(各四类):
男生:
- 零食
- 首饰类
- 小玩偶
- 护肤(化妆)品
女生:
- 自己亲手做的一类物品(画画,蛋糕等)
- 衣服
- 游戏
- 体育用品
1.男生选择礼物的最佳方案
对于男生,我们采用上述四种礼物作为方案层,计算各项指标的得分。
首先,我们使用同样的方式,建立各种物品在4种指标下的权重,并建立判断矩阵,并用MATLAB检验是否满足一致性,代码部分同样在附录之中。
为了节约篇幅,此处直接给出经计算过后的结果:

用CR1,CR2,CR3,CR4个变量分别代表四个判断矩阵的一致性指标,计算结果如下:
| 一致性指标 | 结果大小 |
| CR1 | 0.0790 |
| CR2 | 0.0536 |
| CR3 | 0.0667 |
| CR4 | 0.0380 |
由于4个一致性指标均小于0.1,则可认为上述4个判断矩阵均满足一致性。
接下来计算判断矩阵中的各项权值,计算结果如下表
| 心意 | 权值 |
| 零食 | 0.0759 |
| 首饰类 | 0.4428 |
| 小玩偶 | 0.2310 |
| 化妆品 | 0.2503 |
| 价位 | 权值 |
| 零食 | 0.5235 |
| 首饰类 | 0.0959 |
| 小玩偶 | 0.2951 |
| 化妆品 | 0.0856 |
| 实用性 | 权值 |
| 零食 | 0.5478 |
| 首饰类 | 0.1276 |
| 小玩偶 | 0.0751 |
| 化妆品 | 0.2496 |
| 喜好 | 权值 |
| 零食 | 0.1402 |
| 首饰类 | 0.5192 |
| 小玩偶 | 0.0810 |
| 化妆品 | 0.2596 |
计算完权值后,接下来将计算各个选择(方案)的得分,对应得分与权值相乘后再*100后得到最终得分:
如下表:
| 指标 | 权值 | 零食 | 首饰类 | 小玩偶 | 化妆品 |
| 心意 | 0.4035 | 0.0759 | 0.5235 | 0.5478 | 0.1402 |
| 价位 | 0.1028 | 0.4428 | 0.0959 | 0.1276 | 0.5192 |
| 实用性 | 0.1545 | 0.2310 | 0.2951 | 0.0751 | 0.0810 |
| 喜好 | 0.3402 | 0.2503 | 0.0856 | 0.2496 | 0.2596 |
| 得分 | ------- | 19.698705 | 17.179195 | 34.253791 | 21.393074 |
根据上表可以得知,从男生送礼物的角度考虑,小玩偶是最合适的选择。
2.女生选择礼物的最佳方案:
由于笔者为男性,此处出于客观性考虑,无法建立判断矩阵,故女生的最佳选择这里不予以计算。
四.AHP的理论知识

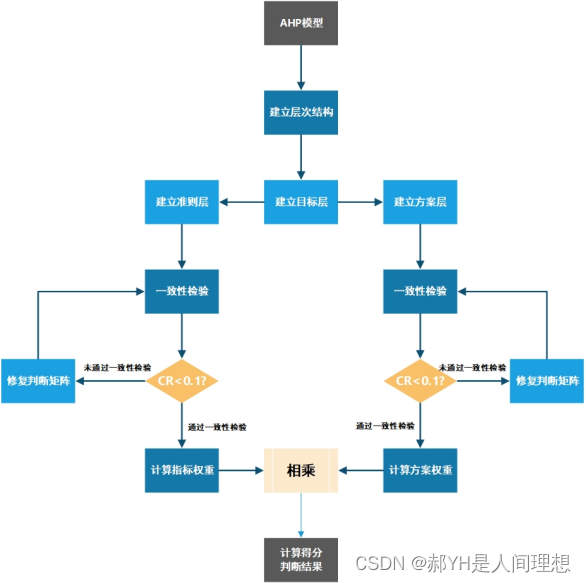
1.建立层次结构
在本次模型建立过程中,目标层——即最终解决的问题是:出于自身情况考虑,哪种礼物更适合送给异性?准则层的4项指标,则是出于送礼物时需要考虑的方向。目标层的4个元素,是在统计分析后抽取出的典例,用于计算得分后给出最佳方案。故对于男生,建立的层次结构如下图所示:
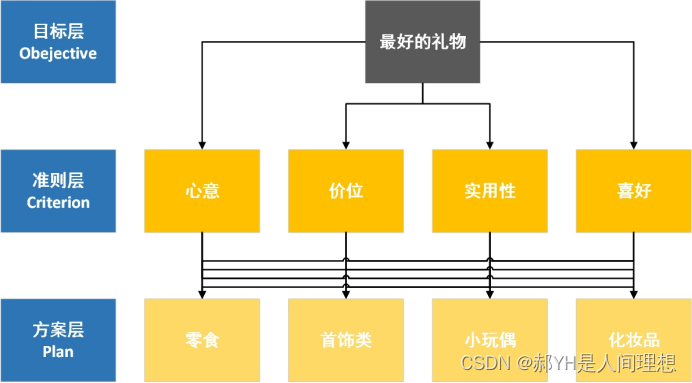
对于女生,出于客观性考虑,本次不建立层次结构,只给出大众化的一个考虑指标权重。
2.构造判断矩阵
对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
本文之前已经给出了准则层与方案层各个元素的判断矩阵,这里不再赘述。
3.计算指标权值
构造出一致性判断矩阵后,对结果进行计算,计算方式为方案层判断矩阵得分乘以准则层判断矩阵权值,此处同样省略计算步骤。
4.计算最终得分(得出目标层)
根据计算结果,选择得分最高的一项作为目标层的结果。本文中男生选礼物的最佳方案为小玩偶。
五.MATLAB代码实现
直接整合到一起了,大家根据注释自行阅读~
%%1.首先计算最大特征值 X= [1,5,3,0.333;0.2,1,0.5,0.2;0.333,2,1,0.333;3,5,3,1];
[V,D] = eig(X);
% 求出A的特征值矩阵D和特征向量V
max_eig=max(max(D));
%获得最大特征值max_eig(拉姆达):4.1580
%%2.计算相关变量,并完成一致性检验
CI = (max_eig - 4) / (4-1);
%%计算一致性指标CI(此处n的值为4)
RI=0.089;
%查表得到随机平均一致性指标,本次总共有4个决策元素(即挑选礼物的指标)
%查表得知n=4时,RI=0.089
CR=CI/RI;
%计算一致性指标
%CR=0.5918,第一次写出的判断矩阵未通过一致性检验,故需要对判断矩阵进行修正。
Y=[1 5 3 1;
0.2 1 0.5 0.25;
0.3333 2 1 0.5;
1 4 2 1;
];
[VN,DN] = eig(Y);
max_eigN=max(max(DN));
CIN = (max_eigN - 4) / (4-1);
RIN=0.089;
CRN=CIN/RIN;
%CR1的值为0.0580,符合一致性检验
%%3.对矩阵进行归一化处理(每一个元素除以其所在列的和)
Sum_Y = sum(Y);
[~,n] = size(Y);
SUM_Y = repmat(Sum_Y,4,1);
%%定义矩阵Stand_Y,即为最后的归一化处理矩阵。
Stand_Y = Y ./ SUM_Y;
%%4.算术平均法计算权重
disp('算术平均法求权重的结果为:');
disp(sum(Stand_Y,2)./4);
%%5.几何平均法计算权重
Prduct_Y = prod(Y,2);
Prduct_4_Y = Prduct_Y .^ (1/4);
disp('几何平均法求权重的结果为:');
disp(Prduct_4_Y ./ sum(Prduct_4_Y));
%%6.特征值法求权重:
[a,b] = eig(Y);
Max_eigN2 = max(max(b));
[r,c]=find(b == Max_eigN2 , 1);
disp('特征值法求权重的结果为:');
disp( a(:,c) ./ sum(a(:,c)) );
%%7.对四个方案层的元素分别构造判断矩阵,并计算权值
%1号矩阵
X1= [1 0.2 0.3333 0.25; 5 1 2 2; 3 0.5 1 1; 4 0.5 1 1;
];
[V1,D1] = eig(X1);
max_eig1=max(max(D1));
CI1 = (max_eig1 - 4) / (4-1);
RI1=0.089;
CR1=CI1/RI1;
Sum_X1 = sum(X1);
[~,n] = size(X1);
SUM_X1 = repmat(Sum_X1,4,1);
Stand_X1 = X1 ./ SUM_X1;
disp('1号矩阵算术平均法求权重的结果为:');
disp(sum(Stand_X1,2)./4);
%2号矩阵 X2= [1 5 2 6;
0.2 1 0.333 1;
0.5 3 1 4;
0.1667 1 0.25 1;
];
[V2,D2] = eig(X2);
max_eig2=max(max(D2));
CI2 = (max_eig2 - 4) / (4-1);
RI2=0.089;
CR2=CI2/RI2;
Sum_X2 = sum(X2);
[~,n] = size(X2);
SUM_X2 = repmat(Sum_X2,4,1);
Stand_X2 = X2 ./ SUM_X2;
disp('2号矩阵算术平均法求权重的结果为:');
disp(sum(Stand_X2,2)./4);
%3号矩阵 X3= [1 5 7 2; 0.2 1 2 0.5;
0.1429 0.5 1 0.3333;
0.5 2 3 1;
];
[V3,D3] = eig(X3);
max_eig3=max(max(D3));
CI3 = (max_eig3 - 4) / (4-1);
RI3=0.089;
CR3=CI3/RI3;
Sum_X3 = sum(X3);
[~,n] = size(X3);
SUM_X3 = repmat(Sum_X3,4,1);
Stand_X3 = X3 ./ SUM_X3;
disp('3号矩阵用算术平均法求权重的结果为::');
disp(sum(Stand_X3,2)./4);
%4号矩阵
X4=[ 1 0.25 2 0.5;
4 1 6 2;
0.5 0.1667 1 0.333;
2 0.5 3 1;
];
[V4,D4] = eig(X4);
max_eig4=max(max(D4));
CI4 = (max_eig4 - 4) / (4-1);
RI4=0.089;
CR4=CI4/RI4;
Sum_X4 = sum(X4);
[~,n] = size(X4);
SUM_X4 = repmat(Sum_X4,4,1);
Stand_X4 = X4 ./ SUM_X4;
disp('4号矩阵用算术平均法求权重的结果为:');
disp(sum(Stand_X4,2)./4); 结束语:本贴旨在通过该例说明AHP的思想,在选择礼物时要结合具体情况谨慎考虑,避免雷区~
相关文章:

MATLAB实现AHP层次分析法——以情人节选取礼物为例
问题背景: 情人节来临之际,广大直男(女)同胞在给异性朋友选购礼物时会遇到难题——什么才是礼物好坏最重要的标准?基于层次分析法AHP进行计算,得出最高权重的指标,给出各位朋友选购礼物的一种思…...

flutter使用Chanel与原生通信
在Flutter中,Platform Channel允许Flutter与原生平台(如Android和iOS)之间进行双向通信,以便在Flutter应用程序和原生代码之间传递消息和调用功能。 以下是使用Platform Channel与原生通信的一般步骤: 1. 在Flutter端…...

Kubernetes技术--k8s核心技术Helm
1.引入 我们先回顾一下之前部署一个应用的过程,如部署nginx,实现效果如下所示: -1.编写deployment的yaml文件,然后运行。 -2.使用service中的NodePort对外暴漏端口 -3.为了弥补Nodeport的缺陷,使用ingress实现转发 这样一个应用就部署完了,这一种情况相对于如果你需要部…...
)
C/C++学习——单例模式(懒汉模式与饿汉模式)
C/C学习——单例模式 一、什么是单例模式?二、单例模式应用三、单例模式的特点注意:静态成员变量的使用示例代码: 四、单例模式C代码示例(饿汉模式)五、单例模式C示例代码(懒汉模式) 一、什么是…...

企业微信网页开发本地调试方式
一、开启企业微信调试模式 首先在企业微信打开一个网页应用时,其实就是打开了一个微信环境的浏览器,此时想要检查网页元素,查看请求接口,需要开启调试模式。企业微信默认是不支持调试的,需要再单独下载一个文件放在安…...

Prompt GPT推荐社区
大家好,我是荷逸,这次给大家带来的是我日常学习Prompt社区推荐 Snack Prompt 访问地址:http://snackprompt.com Snack Prompt是一个采用的Prompts诱导填空式的社区,它提供了一种简单的prompt修改方式,你只需要输入关…...
小程序隐私保护授权处理方式之弹窗组件
欢迎点击关注-前端面试进阶指南:前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 小程序隐私保护授权弹窗组件 调用wx.getUserProfile进行授权时,返回错误信息:{errMsg: “getUserProfile:fail api scope is…...

Java 复习笔记 - 方法篇
文章目录 一,方法的定义二,最简单的方法定义和调用三,带参数的方法定义和调用四,带返回值方法的定义和调用五,小结六,方法的重载七,方法简单练习1,数组遍历2,数组最大值3…...

大数据到底是好是坏?_光点科技
近年来,随着科技的不断发展和互联网的普及,大数据已经成为一个备受关注的话题。它带来了许多机遇和挑战,引发了人们对于其是好是坏的争议。大数据究竟是一把双刃剑,需要我们从多个角度来审视。 大数据的好处无疑是显而易见的。首先…...
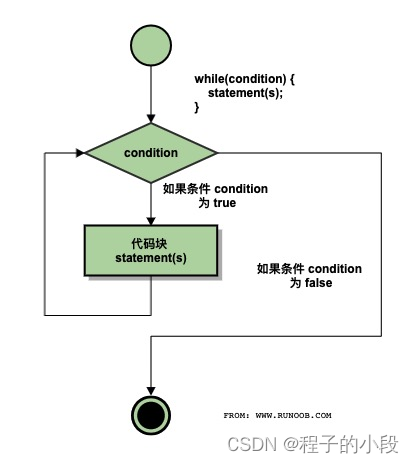
C++ while 循环
只要给定的条件为真,while 循环语句会重复执行一个目标语句。 语法 C 中 while 循环的语法: while(condition) {statement(s); }在这里,statement(s) 可以是一个单独的语句,也可以是几个语句组成的代码块。condition 可以是任意…...

orm_sqlalchemy总结
sqlalchemy使用总结 1 sqlalchemy ORM基础操作 官方文档:https://docs.sqlalchemy.org/en/13/orm/tutorial.html 创建连接 - 创建基类 - 创建实体类 - 创建表 - 创建session import logging import pymysql from pymysql.cursors import DictCursor import sqla…...
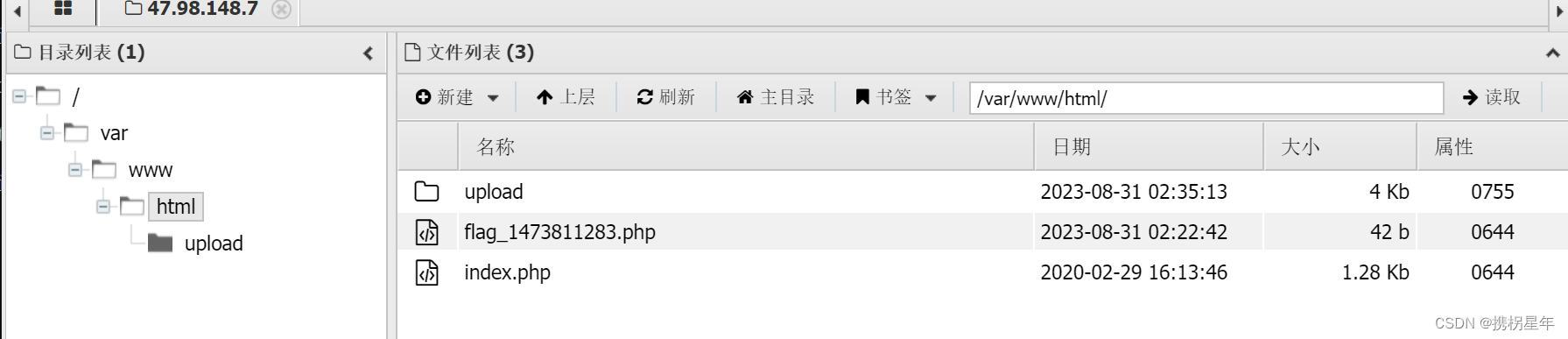
CTFhub-文件上传-MIME绕过
用哥斯拉生成 php 木马文件 1.php 抓包---> 修改 conten-type 类型 为 imge/jpeg 用蚁剑连接 ctfhub{8e6af8109ca15932bad4747a}...

【校招VIP】前端校招考点之UDP
考点介绍: UDP是非面向连接协议,使用udp协议通讯并不需要建立连接,它只负责把数据尽可能发送出去,并不可靠,在接收端,UDP把每个消息断放入队列中,接收端程序从队列中读取数据。 『前端校招考点…...
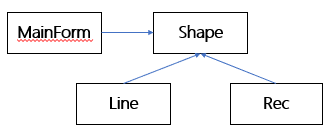
C++设计模式_02_面向对象设计原则
文章目录 1. 面向对象设计,为什么?2. 重新认识面向对象3. 面向对象设计原则3.1 依赖倒置原则(DIP)3.2 开放封闭原则(OCP )3.3 单一职责原则( SRP )3.4 Liskov 替换原则 ( LSP )3.5 接口隔离原则 ( ISP )3.6 优先使用对象组合,而不是类继承3.7…...
springcloud-gateway简述
Spring Cloud Gateway 是一个用于构建 API 网关的项目,它是 Spring Cloud 生态系统中的一部分,旨在为微服务架构提供动态路由、负载均衡、安全性和监控等功能。 网关工程对应pom文件 <?xml version"1.0" encoding"UTF-8"?>…...
【大虾送书第七期】深入浅出SSD:固态存储核心技术、原理与实战
目录 ✨写在前面 ✨内容简介 ✨作者简介 ✨名人推荐 ✨文末福利 🦐博客主页:大虾好吃吗的博客 🦐专栏地址:免费送书活动专栏地址 写在前面 近年来国家大力支持半导体行业,鼓励自主创新,中国SSD技术和产业…...

常见矿石材质鉴定VR实训模拟操作平台提高学员的学习效果和实践能力
随着“元宇宙”概念的不断发展,在矿山领域中,长期存在传统培训内容不够丰富、教学方式单一、资源消耗大等缺点,无法适应当前矿山企业发展需求的长期难题。元宇宙企业借助VR虚拟现实、web3d开发和计算机技术构建的一个虚拟世界,为用…...

Verilog 学习路线
参考知乎 首先得学习数电和 Verilog 基础。 常问的 Verilog 基础 二分频是怎么写的 阻塞和非阻塞及其应用 写一个100MHz的时钟 Reg 和 wire 的区别 Logic 和 wire 的区别,两者可以转换吗 用你最擅长的语言找出1-100的质数 一个最简单的八位加法器应该怎么验…...
前端三剑客中简单的两个:HTMLCSS
HTML&CSS 1,HTML1.1 介绍1.2 快速入门1.3 基础标签1.3.1 标题标签1.3.2 hr标签1.3.3 字体标签 1.4 图片、音频、视频标签1.5 超链接标签1.6 列表标签1.7 表格标签1.8 布局标签1.9 表单标签1.9.1 表单标签概述1.9.2 form标签属性1.9.3 代码演示 1.10 表单项标签 …...
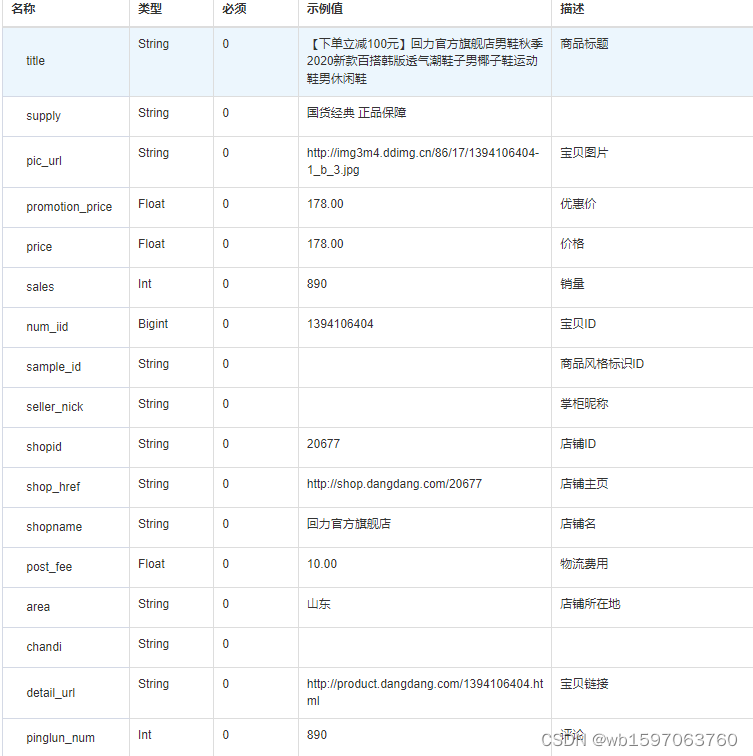
Java实现根据关键词搜索当当商品列表数据方法,当当API接口申请指南
要通过当当网的API获取商品列表数据,您可以使用当当开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过当当开放平台API获取商品列表: 首先,确保您已注册成为当当开放平台的开发者,并创建…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...