freee Programming Contest 2023(AtCoder Beginner Contest 310)
文章目录
- A - Order Something Else(模拟)
- B - Strictly Superior(模拟)
- C - Reversible(模拟)
- D - Peaceful Teams(DFS+状压)
- E - NAND repeatedly(普通dp)
- F - Make 10 Again(状态压缩+概率dp)
- G - Takahashi And Pass-The-Ball Game(倍增/内向基环树)
A - Order Something Else(模拟)
题意:两种方式购买饮料,一种是直接购买,一种是使用优惠券购买,使用优惠券购买,但是必须买一个小菜。
思路:模拟。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 3005;
void solve() {int n, p, q;cin >> n >> p >> q;int mn = 0x3f3f3f3f;for (int i = 0; i < n; i++) {int x;cin >> x;mn = min(mn, x);}cout << min(p, q + mn) << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;// cin >> T;while (T--) {solve();}return 0;
}
B - Strictly Superior(模拟)
题意:有n个产品,第i个产品价格为pi,有ci个功能,问是否有严格更优的产品。定义严格更优的产品优以下特征:
- P i ⩾ P j P_i\geqslant{P_j} Pi⩾Pj
- 第j个含有第i个所有功能
- 第j个价格严格更少,或者功能严格更多。
思路:模拟。
代码:
int mark[105][105];
int p[105], c[105];
void solve() {int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> p[i] >> c[i];for (int j = 0; j < c[i]; j++) {int x;cin >> x;mark[i][x] = 1;}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j || p[i] < p[j]) continue;int flag = 1;for (int k = 0; k <= m; k++) {if (mark[i][k] > mark[j][k]) {flag = 0;break;}}if (!flag) continue;if (p[i] > p[j] || c[j] > c[i]) {cout << "Yes\n";return;}}}cout << "No\n";
}
C - Reversible(模拟)
题意:完全相同和恰好相反的字符串是相同的,求出这里所有不同的字符串。
思路:正向和方向取字典序最小放入集合中即可。
拓展:如果是要求循环同构条件下本质不同的字符串,可以使用最小表示法,或者后缀数组来实现求出字典序最小的位置,放入集合中即可,均可以实现线性复杂度找到最小字典序位置。
代码:
void solve() {int n;cin >> n;set<string> st;for (int i = 0; i < n; i++) {string s;cin >> s;string t = s;reverse(s.begin(), s.end());st.insert(min(s, t));}cout << st.size() << '\n';
}
D - Peaceful Teams(DFS+状压)
题意:有n个队员,但是其中m对不和睦的关系,现在要想划分成t个队伍,求出所有合法的不同的划分。
思路:暴力,这里的n最大为10,划分成t组,朴素暴力的时间复杂度是 O ( n t ) O(n^t) O(nt) 1e10数量级,无法承受。利用状态压缩,用一个数来代表一个小队,然后判断当前人是加入已有小队还是另外创建小队分类dfs,这样时间复杂度降到 O ( n ! ) O(n!) O(n!) 10!只有3,628,800。
理念:考虑划分可能有些困难,可以用动态规划的思想,就是考虑前i个的时候有哪些划分,例如,只有一个人的时候,就只能自成一队,当前i个人组成了dp[i]种划分时,此时再加入一个人,他可以选择加入现有的队,或者自成一队,这两者是互斥的。
注意:一定要预先分配内存块(reserve),否则,递归的时候,扩容的话可能会转移vector,导致上一个递归内存帧的迭代器失效。
代码:
int mask[15];
vector<int> teams;
//dfs遍历所有可能的划分情况
//now是单调递增的,根据动态规划的思想,考虑加入现有队伍或者自成一队的情况
//对于前面i种所有本质不同的划分,插入一个新的now,对于不同划分之间仍然保持本质不同。
//对于同一划分,不同插入位置也本质不同,因此这样是完备的。
int dfs(int now) {if (now == n + 1) {return teams.size() == t;}int ans = 0;for (int& team : teams) {//auto&!if (!(team & mask[now])) {team |= 1 << now;ans += dfs(now + 1);team ^= 1 << now;}}if (teams.size() < t) {teams.push_back(1 << now);ans += dfs(now + 1);teams.pop_back();}return ans;
}
void solve() {cin >> n >> t >> m;teams.reserve(t);for (int i = 0; i < m; i++) {int x, y;cin >> x >> y;mask[y] |= 1 << x;//都是拿大的去找小的}cout << dfs(1) << '\n';
}
E - NAND repeatedly(普通dp)
题意:给出一个01序列,求所有的非合取连续子段和。
思路:dp即可,dp表示所有以i结尾的非零后缀数,如果这位是0,那么,此处的贡献是i-1(注意这个运算,0的话任意后缀均可,除了单个零);如果是1,此处是1(独立一个数,最小的后缀)+(i-1) - dp(i-1)(表示以i-1为结尾所有为0的后缀,全部后缀减去非零后缀)。
d p i = { 1 + i − 1 − d p i − 1 s i 为 1 i − 1 s i 为 0 dp_i=\left\{ \begin{matrix} 1 + i-1-dp_{i-1}~~~~s_i为1\\ i-1~~~~s_i为0 \end{matrix} \right. dpi={1+i−1−dpi−1 si为1i−1 si为0
void solve() {int n;cin >> n;string s;cin >> s;int last = 0, cnt = 0;long long ans = 0;for (auto x : s) {if (x == '0') {ans += cnt;last = cnt;} else {last = 1 + cnt - last;ans += last;}cnt++;}cout << ans << '\n';
}
拓展:如果是求一个序列所有的连续子段异或和,这些数是int范围内,那么我们可以拆成32位,统计各位的贡献次数。普通异或的情况下。最后加权求和即可。
d p i = { 1 + i − 1 − d p i − 1 s i 为 1 d p i − 1 s i 为 0 dp_i=\left\{ \begin{matrix} 1 + i-1-dp_{i-1}~~~~s_i为1\\ dp_{i-1}~~~~s_i为0 \end{matrix} \right. dpi={1+i−1−dpi−1 si为1dpi−1 si为0
F - Make 10 Again(状态压缩+概率dp)
题意:给定N个骰子,每个骰子有Ai个面,问同时抛出这些骰子有多大的概率得到10
前言:如何设计状态?不同的概率对应有情况的不同划分,把诸多的骰子组合完整地划分成若干情况,使得这些情况的概率方便计算,方便推演是我们的目标。当然,我们可以将最后N个骰子的情况,简单地划分成两种情况,这些骰子能组成10的和这些骰子不能组成10的,但是这样划分太过粗糙,每种情况都有诸多的子情况,比较难以计算,不方便递推,尽管这样同样是合法的——这两种情况互不包含,并且涵盖了所有的情况。这里,我们可以把最后骰子的情况,划分成这些骰子能够组成的所有数的集合,这样有一个优异的性能,我们可以通过先前的集合和当前骰子的情况,推算该骰子所能转移到的所有能够抵达的状态,如果我们不选择这个集合,我们可以有原先的集合S都可以取到, 有 1 A i 概率 , T = { x ∈ S ∣ x + j ( j ∈ [ 1 , A i ] ] ) } 有\frac{1}{A_i}概率,T=\{x\in S\;|\;x+j(j\in[1,A_i]])\} 有Ai1概率,T={x∈S∣x+j(j∈[1,Ai]])},那么当前概率下可以抵达的状态便是 S ∪ T S\cup T S∪T,对于当前骰子等概率的各种情况,我们都能转移到前i+1个骰子的各种状态,更进一步,我们可以不考虑大于10的部分,我们于是将原先所有的情况,按照能够组成0~10这11个数的情况划分成2^11类型,这些类型完全涵盖了所有骰子状态,并且这些情况不会互相重叠。当我们考虑玩当前所有集合,所有骰子的情况,我们就能完整且不遗漏地得到得到当前所有骰子的所有状态的概率
思路: d p [ N ] [ m a s k ] dp[N][mask] dp[N][mask]表示,考虑前N个骰子的情况,够组合成这个mask集合的概率。
边界
d p [ 0 ] [ S ] = { 0 i f S ≠ { 0 } 1 i f S = { 0 } dp[0][S]=\left\{ \begin{array}{l} 0\quad if\;S\neq \{0\}\\ 1\quad if\;S=\{0\}\\ \end{array} \right. dp[0][S]={0ifS={0}1ifS={0}
转移
∀ i , S , j ∈ [ 1 , A i ] , d p [ i ] [ S ] → d p [ i + 1 ] [ S ∪ T ] 其中 T = { x ∈ S ∣ x + j ( j ∈ [ 1 , A i ] ] ) } \forall i,S, j\in{[1,A_i]},dp[i][S]\rightarrow dp[i+1][S\cup T]其中T=\{x\in S\;|\;x+j(j\in[1,A_i]])\} ∀i,S,j∈[1,Ai],dp[i][S]→dp[i+1][S∪T]其中T={x∈S∣x+j(j∈[1,Ai]])}
答案
∑ 10 ∈ S d p [ N ] [ S ] \sum_{10\in S}dp[N][S] 10∈S∑dp[N][S]
时间复杂度
O ( 10 N 2 11 ) O(10N2^{11}) O(10N211)
约4e6
ll po(ll rad, ll idx) {ll res = 1;while (idx) {if (idx & 1) res = res * rad % mod;idx >>= 1;rad = rad * rad % mod; }return res;
}int mask = (1 << 11) - 1;
ll f[105][1 << 11];void solve() {f[0][1] = 1;int n;cin >> n;for (int i = 1; i <= n; i++) {int x;cin >> x;ll inv = po(x, mod - 2);for (int j = 1; j <= min(x, 10); j++) {for (int k = 0; k <= mask; k++) {int u = (k | (k << j)) & mask;f[i][u] = (f[i][u] + f[i - 1][k] * inv % mod) % mod;}}if (x > 10) {//取并了等于没有取,统一处理for (int k = 0; k <= mask; k++) {f[i][k] = (f[i][k] + f[i - 1][k] * inv % mod * (x - 10) % mod) % mod;}}}ll ans = 0;for (int i = 0; i <= mask; i++) {if (i & (1 << 10)) {ans = (ans + f[n][i]) % mod;}}cout << ans << '\n';
}
G - Takahashi And Pass-The-Ball Game(倍增/内向基环树)
题意:这里有 N N N个高桥君(这是Atcoder的社长),第 i i i个高桥君一个整数 A i A_i Ai和 B i B_i Bi个球。给定一个 K K K,等概率地选择 x , x ∈ [ 1 , K ] x,x\in[1,K] x,x∈[1,K],之后他们互相传球,第 i i i个高桥君,把球传给第 A i A_i Ai个高桥君,注意,他们是同时传球的,传 x x x次。求出每个高桥君手里的球的数量的期望。
思路:这里是倍增的方法。等概率 [ 1 , K ] [1,K] [1,K],我们最后答案是 ∑ i = 1 K 1 K f ( i ) \sum_{i=1}^K\frac{1}{K}{f(i)} ∑i=1KK1f(i), f ( x ) f(x) f(x)表示 x x x次时,某个高桥君在手上的球的数目的。求期望,我们首先,可以求出 1 1 1到 K K K的时候,各个高桥君手里球的数目,然后除以 K K K即可。
如何计算呢?
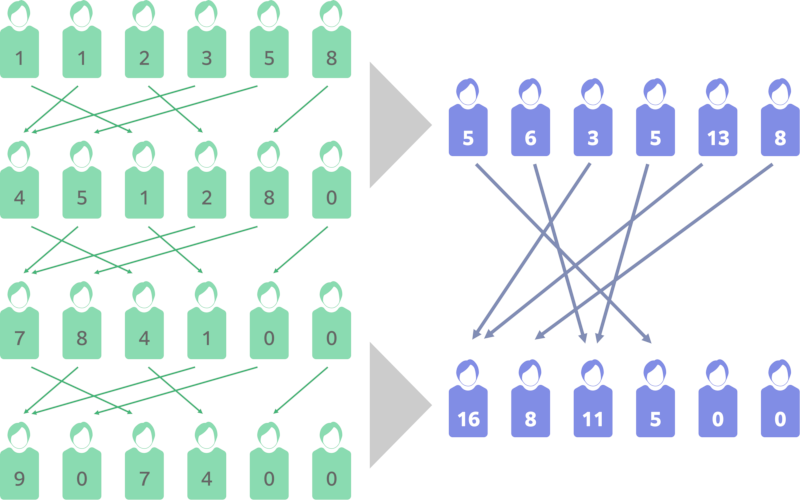
上图是传三次球的情况,我们最终的答案是后三排的和数组,因为不能传零次。如果是偶数排,我们可以把两排并作一排,我们可以传一次球累加得到绿色的第一排和第二排的和,也就是右侧蓝色的第一排,显然我们不能同样地算出蓝色第二排,因为 K K K非常大,我们要用快速幂的思想,蓝色第二排,也就是绿色第三排,绿色第四排的和,注意看,绿色第三排的球来自绿色第一排传两次的球,绿色第四排的球来自绿色第二排传两次的球,如果我们把绿色第一排和绿色第二排作为一个整体,那么相当于,这个整体连传两次球到绿色第三排和绿色第四排的整体,我们对传球关系进行迭代运算,可以得到右侧蓝色两排传直球的关系,经过这样的操作,总排数便减少了一半。传球有平行关系!
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mod = 998244353;ll po(ll rad, ll idx) {ll res = 1;rad %= mod;//炸long long!!!while (idx) {if (idx & 1) res = res * rad % mod;idx >>= 1;rad = rad * rad % mod; }return res;
}void solve() {int n;ll k;cin >> n >> k;vector<ll> A(n), B(n);vector<ll> ans(n);for (int i = 0; i < n; i++) {cin >> A[i];A[i]--;}for (int i = 0; i < n; i++) {cin >> B[i];ans[i] = mod - B[i];//减去第一排}ll inv = po(k, mod - 2);k++;//k+1排while (k) {if (k & 1) {//取走一排for (int i = 0; i < n; i++) {ans[i] = (ans[i] + B[i]) % mod;}//传一次球vector<ll> tmp(n);for (int i = 0; i < n; i++) {tmp[A[i]] = (tmp[A[i]] + B[i]) % mod;}B = tmp;}//两排并一排vector<ll> tmp(n);//传一次球for (int i = 0; i < n; i++) {tmp[A[i]] = (tmp[A[i]] + B[i]) % mod;}for (int i = 0; i < n; i++) {B[i] = (B[i] + tmp[i]) % mod;}//关系迭代vector<ll> AA(n);for (int i = 0; i < n; i++) {AA[i] = A[A[i]];} A = AA;k >>= 1;}for (int i = 0; i < n; i++) {cout << ans[i] * inv % mod << " \n"[i == n - 1];}
}
相关文章:

freee Programming Contest 2023(AtCoder Beginner Contest 310)
文章目录 A - Order Something Else(模拟)B - Strictly Superior(模拟)C - Reversible(模拟)D - Peaceful Teams(DFS状压)E - NAND repeatedly(普通dp)F - Make 10 Again(状态压缩概率dp&#x…...

恒运资本:概念股是什么意思
概念股是指在特定的经济布景、方针环境、职业远景或社会热点等方面具有某种特别的发展远景和投资价值的股票。在投资者心目中,概念股的危险较大,可是或许带来高于商场平均水平的收益率。那么,概念股到底是什么意思?在本文中&#…...
十九、状态模式
一、什么是状态模式 状态(State)模式的定义:对有状态的对象,把复杂的“判断逻辑”提取到不同的状态对象中,允许状态对象在其内部状态发生改变时改变其行为。 状态模式包含以下主要角色: 环境类(…...
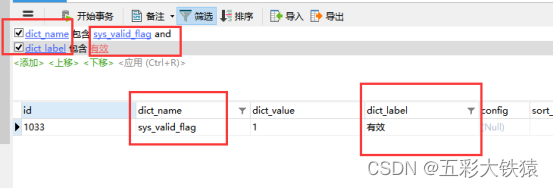
MySQL用navicat工具对表进行筛选查找
这个操作其实很简单,但是对于没操作的人来说,就是不会呀。所以小编出这一个详细图解,希望能够帮助到大家。话不多说看图。 第一步: 点进一张表,点击筛选。 第二步: 点击添加 第三步: 选择要…...

音视频 ffplay简单过滤器
视频旋转 ffplay -i test.mp4 -vf transpose1视频反转 ffplay test.mp4 -vf hflip ffplay test.mp4 -vf vflip视频旋转和反转 ffplay test.mp4 -vf hflip,transpose1音频变速播放 ffplay -i test.mp4 -af atempo2视频变速播放 ffplay -i test.mp4 -vf setptsPTS/2音视频同…...

索引 事务 存储引擎
################索引##################### 一、索引的概念 ●索引是一个排序的列表,在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址(类似于C语言的链表通过指针指向数据记录的内存地址)。 ●使用索引后可以不用扫描全表来…...
MySQL— 基础语法大全及操作演示!!!(事务)
MySQL—— 基础语法大全及操作演示(事务) 六、事务6.1 事务简介6.2 事务操作6.2.1 未控制事务6.2.2 控制事务一6.2.3 控制事务二 6.3 事务四大特性6.4 并发事务问题6.5 事务隔离级别 MySQL— 基础语法大全及操作演示!!!…...
xsschallenge1~13通关详细教程
文章目录 XSS 挑战靶场通关level1level2level3level4level5level6level7level8level9level10level11level12level13 XSS 挑战靶场通关 level1 通过观察发现这个用户信息可以修改 那么我们直接输入攻击代码 <script>alert(/wuhu/)</script>弹框如下: …...

考生作弊行为分析算法
考生作弊行为分析系统利用pythonyolo系列网络模型算法框架,考生作弊行为分析算法利用图像处理和智能算法对考生的行为进行分析和识别,经过算法服务器的复杂计算和逻辑判断,算法将根据考生行为的特征和规律,判定是否存在作弊行为。…...

Python 操作 Redis 数据库介绍
Redis 作为常用的 NoSql 数据库,主要用于缓存数据,提高数据读取效率,那在 Python 中应该如果连接和操作 Redis 呢?今天就为大概简单介绍下,在 Python 中操作 Redis 常用命令。 安装 redis 首先还是需要先安装 redis …...

十年JAVA搬砖路——软件工程概述
软件工程是一门关注软件开发过程的学科,它涉及到软件的设计、开发、测试、部署和维护等方面。软件工程的目标是通过系统化的方法和工具,以确保软件项目能够按时、按预算和按要求完成。 • 软件工程的7个基本概念: 软件生命周期:软…...
前后端项目部署上线详细笔记
部署 参考文章:如何部署网站?来比比谁的方法多 - 哔哩哔哩大家好,我是鱼皮,不知道朋友们有没有试着部署过自己开发的网站呢?其实部署网站非常简单,而且有非常多的花样。这篇文章就给大家分享几种主流的前端…...
Android 蓝牙开发( 二 )
前言 上一篇文章给大家分享了Android蓝牙的基础知识和基础用法,不过上一篇都是一些零散碎片化的程序,这一篇给大家分享Android蓝牙开发实战项目的初步使用 效果演示 : Android蓝牙搜索,配对,连接,通信 Android蓝牙实…...
C#调用barTender打印标签示例
使用的电脑需要先安装BarTender 我封装成一个类 using System; using System.Windows.Forms;namespace FT_Tools {public class SysContext{public static BarTender.Application btapp new BarTender.Application();public static BarTender.Format btFormat;public void Q…...
Spring——Spring读取文件
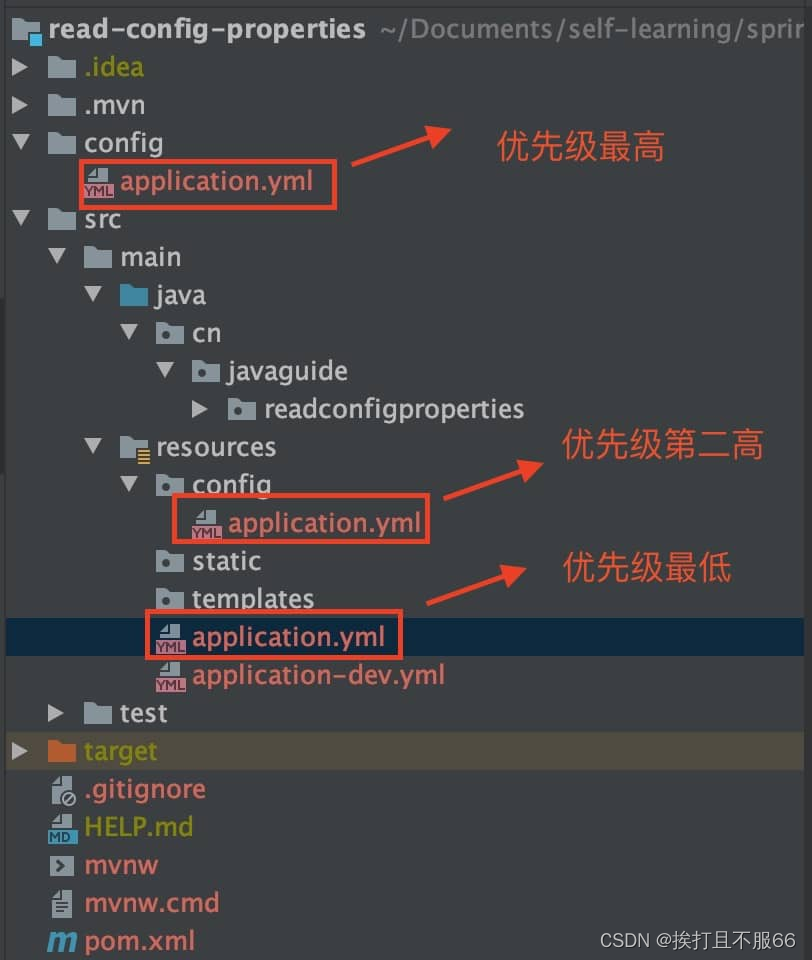
文章目录 1.通过 value 读取比较简单的配置信息2.通过ConfigurationProperties读取并与 bean 绑定3.通过ConfigurationProperties读取并校验4. PropertySource 读取指定 properties 文件5.题外话:Spring加载配置文件的优先级 很多时候我们需要将一些常用的配置信息比如阿里云os…...

这是一条求助贴(postman测试的时候一直是404)
看到这个问题是404的时候总感觉不该求助大家,404多常见一看就是简单的路径问题,我的好像不是,我把我的问题奉上。 首先我先给出我的url http://10.3.22.195:8080/escloud/rest/escloud_contentws/permissionStatistics/jc-haojl/sz 这是我…...
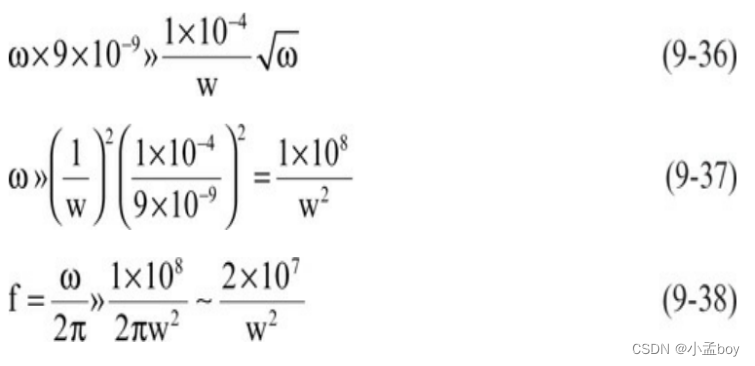
信号完整性分析基础知识之有损传输线、上升时间衰减和材料特性(四):有损传输线建模
传输线中信号衰减的两个损耗过程是通过信号和返回路径导体的串联电阻以及通过有损耗介电材料的分流电阻。这两个电阻器的电阻都与频率相关。 值得注意的是,理想电阻器的电阻随频率恒定。我们已经证明,在理想的有损传输线中,用于描述损耗的两个…...
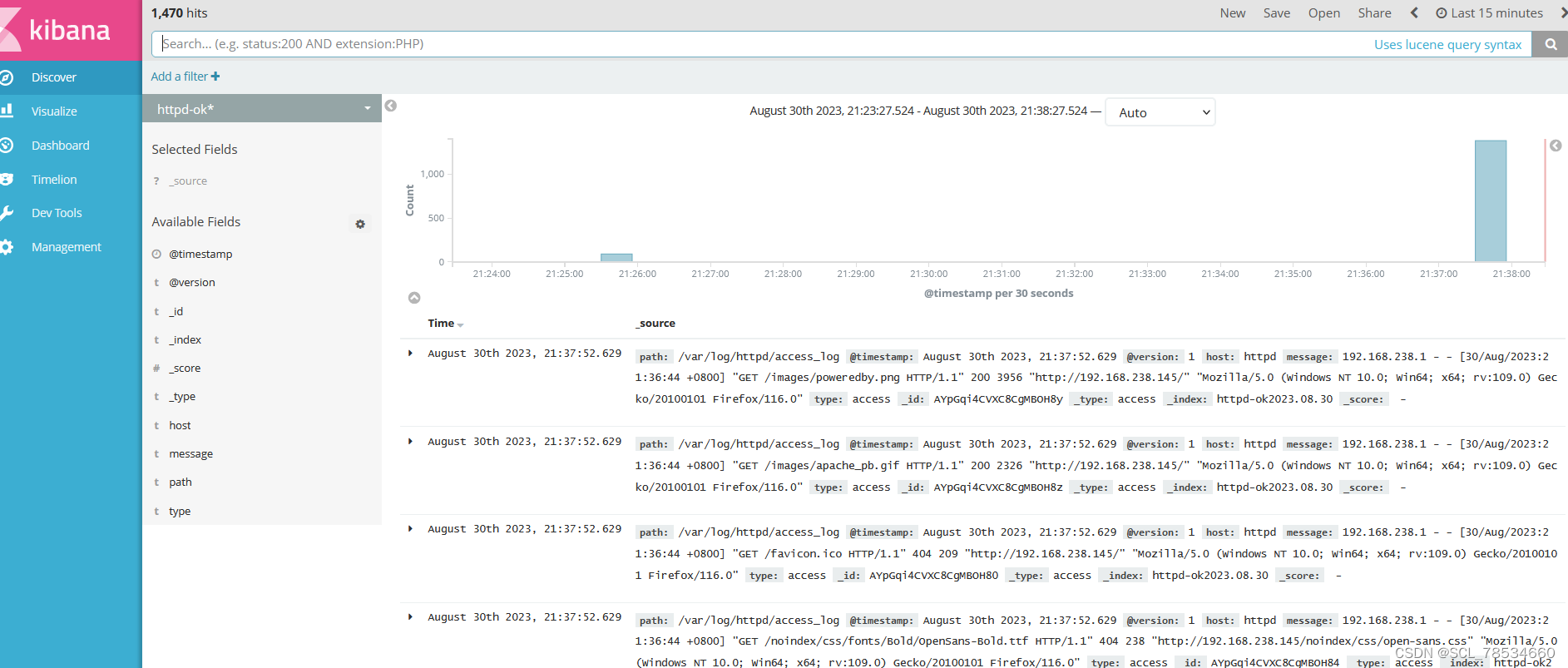
elk日志收集系统
目录 前言 一、概述 二、案例 (一)、环境配置 安装node1与node2节点的elasticsearch node1的elasticsearch-head插件 (二)、node1服务器安装logstash 测试1: 标准输入与输出 测试2:使用rubydebug解…...

perl 语言中 AUTOLOAD 的用法
这里的 AUTOLOAD可以理解为自动加载。具体来说就是,在正常情况下,我们不能调用一个尚未定义的函数(子例程)。不过,如果在未定义函数的包中有一个名为 AUTOLOAD的函数,那么对未定义函数的调用都会路由至这个…...
服务器放在香港好用吗?
相较于国内服务器,将网站托管在香港服务器上最直观的好处是备案层面上的。香港服务器上的网站无需备案,因此更无备案时限,购买之后即可使用。 带宽优势 香港服务器的带宽一般分为香港本地带宽和国际带宽、直连中国骨干网 CN2三种。香港…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
