运用谱分解定理反求实对称矩阵
文章目录
- 谱分解定理
- 定理的运用
谱分解定理
设三阶实对称矩阵 A A A,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3,对应的单位化特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3 且两两正交,则 A = λ 1 α 1 α 1 T + λ 2 α 2 α 2 T + λ 3 α 3 α 3 T A = \lambda_1 \alpha_1 \alpha_1^{\mathrm{T}} + \lambda_2 \alpha_2 \alpha_2^{\mathrm{T}} + \lambda_3 \alpha_3 \alpha_3^{\mathrm{T}} A=λ1α1α1T+λ2α2α2T+λ3α3α3T。
【注 1】在考研范围内,只适用于实对称矩阵。
【注 2】特征向量必须两两正交且单位化!
证明:三阶实对称矩阵 A A A 可相似对角化,存在正交矩阵 Q = ( α 1 , α 2 , α 3 ) Q=(\alpha_1,\alpha_2,\alpha_3) Q=(α1,α2,α3),使得 Q T A Q = Λ = [ λ 1 λ 2 λ 3 ] Q^{\mathrm{T}}AQ = \Lambda = \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} QTAQ=Λ= λ1λ2λ3 。
所以有: A = ( α 1 , α 2 , α 3 ) [ λ 1 λ 2 λ 3 ] [ α 1 T α 2 T α 3 T ] = λ 1 α 1 α 1 T + λ 2 α 2 α 2 T + λ 3 α 3 α 3 T A = (\alpha_1,\alpha_2,\alpha_3) \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} \begin{bmatrix} \alpha_1^{\mathrm{T}} \\ \alpha_2^{\mathrm{T}} \\ \alpha_3^{\mathrm{T}} \end{bmatrix} = \lambda_1 \alpha_1 \alpha_1^{\mathrm{T}} + \lambda_2 \alpha_2 \alpha_2^{\mathrm{T}} + \lambda_3 \alpha_3 \alpha_3^{\mathrm{T}} A=(α1,α2,α3) λ1λ2λ3 α1Tα2Tα3T =λ1α1α1T+λ2α2α2T+λ3α3α3T。
定理的运用
什么时候运用谱分解定理最方便?
(1)当特征值出现 0 0 0 时,运用定理可减少计算量(参见解法一);
(2)当特征值出现二重根 k k k 时,可先运用定理计算出具体的 A − k E A-kE A−kE,再算出实对称矩阵 A A A(参见解法二);
(3)运用该定理甚至不需要求出所有的特征向量!
【例】设 3 3 3 阶实对称矩阵 A A A 的秩为 2 2 2, λ 1 = λ 2 = 6 \lambda_1=\lambda_2=6 λ1=λ2=6 是 A A A 的二重特征值,若 α 1 = ( 1 , 1 , 0 ) T , α 2 = ( 2 , 1 , 1 ) T , α 3 = ( − 1 , 2 , − 3 ) T \alpha_1=(1,1,0)^{\mathrm{T}},\alpha_2=(2,1,1)^{\mathrm{T}},\alpha_3=(-1,2,-3)^{\mathrm{T}} α1=(1,1,0)T,α2=(2,1,1)T,α3=(−1,2,−3)T,都是 A A A 属于特征值 6 6 6 的特征向量,求矩阵 A A A。
【解法一】由 r ( A ) = 2 r(A)=2 r(A)=2 可得特征值 λ 1 = λ 2 = 6 , λ 3 = 0 \lambda_1=\lambda_2=6, \lambda_3=0 λ1=λ2=6,λ3=0,将 α 1 = ( 1 , 1 , 0 ) T , α 2 = ( 2 , 1 , 1 ) T \alpha_1=(1,1,0)^{\mathrm{T}},\alpha_2=(2,1,1)^{\mathrm{T}} α1=(1,1,0)T,α2=(2,1,1)T 进行单位正交化得: ξ 1 = 1 2 ( 1 , 1 , 0 ) T , ξ 2 = 1 6 ( 1 , − 1 , 2 ) T \xi_1 = \frac{1}{\sqrt{2}} (1,1,0)^{\mathrm{T}},\xi_2 = \frac{1}{\sqrt{6}}(1,-1,2)^{\mathrm{T}} ξ1=21(1,1,0)T,ξ2=61(1,−1,2)T。
运用谱分解定理:
A = λ 1 ξ 1 ξ 1 T + λ 2 ξ 2 ξ 2 T = 3 ξ 1 ξ 1 T + ξ 2 ξ 2 T = 3 [ 1 1 0 ] ( 1 , 1 , 0 ) + [ 1 − 1 2 ] ( 1 , − 1 , 2 ) = [ 4 2 2 2 4 − 2 2 − 2 4 ] \begin{aligned} A &= \lambda_1 \xi_1 \xi_1^{\mathrm{T}} + \lambda_2 \xi_2 \xi_2^{\mathrm{T}} \\ &= 3 \xi_1 \xi_1^{\mathrm{T}} + \xi_2 \xi_2^{\mathrm{T}} \\ &= 3 \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} (1,1,0) + \begin{bmatrix} 1 \\ -1 \\ 2 \end{bmatrix} (1,-1,2) \\ &= \begin{bmatrix} 4 & 2 & 2 \\ 2 & 4 & -2 \\ 2 & -2 & 4 \end{bmatrix} \end{aligned} A=λ1ξ1ξ1T+λ2ξ2ξ2T=3ξ1ξ1T+ξ2ξ2T=3 110 (1,1,0)+ 1−12 (1,−1,2)= 42224−22−24
【解法二】先求出 A A A 的另一特征值和对应的特征向量 λ 3 = 0 , α 3 = ( − 1 , 1 , 1 ) T \lambda_3=0,\alpha_3=(-1,1,1)^{\mathrm{T}} λ3=0,α3=(−1,1,1)T,进行单位正交化: ξ 3 = 1 3 ( − 1 , 1 , 1 ) T \xi_3=\frac{1}{\sqrt{3}}(-1,1,1)^{\mathrm{T}} ξ3=31(−1,1,1)T。
由于 A A A 的特征值为 λ 1 = λ 2 = 6 , λ 3 = 0 \lambda_1=\lambda_2=6, \lambda_3=0 λ1=λ2=6,λ3=0,所以 A − 6 E A-6E A−6E 的特征值为 λ 1 = λ 2 = 0 , λ 3 = − 6 \lambda_1=\lambda_2=0, \lambda_3=-6 λ1=λ2=0,λ3=−6,注意到其对应的特征向量仍然不变,因此可以先求出 A − 6 E A-6E A−6E,运用谱分解定理:
A − 6 E = λ 3 ξ 3 ξ 3 T = − 2 [ − 1 1 1 ] ( − 1 , 1 , 1 ) = [ − 2 2 2 2 − 2 − 2 2 − 2 − 2 ] \begin{aligned} A-6E &= \lambda_3 \xi_3 \xi_3^{\mathrm{T}} \\ &= -2 \begin{bmatrix} -1 \\ 1 \\ 1 \end{bmatrix} (-1,1,1) \\ &= \begin{bmatrix} -2 & 2 & 2 \\ 2 & -2 & -2 \\ 2 & -2 & -2 \end{bmatrix} \end{aligned} A−6E=λ3ξ3ξ3T=−2 −111 (−1,1,1)= −2222−2−22−2−2
所以有:
A = ( A − 6 E ) + 6 E = [ − 2 2 2 2 − 2 − 2 2 − 2 − 2 ] + [ 6 6 6 ] = [ 4 2 2 2 4 − 2 2 − 2 4 ] \begin{aligned} A &= (A-6E) + 6E \\ &= \begin{bmatrix} -2 & 2 & 2 \\ 2 & -2 & -2 \\ 2 & -2 & -2 \end{bmatrix} + \begin{bmatrix} 6 & & \\ & 6 & \\ & & 6 \end{bmatrix} \\ &= \begin{bmatrix} 4 & 2 & 2 \\ 2 & 4 & -2 \\ 2 & -2 & 4 \end{bmatrix} \end{aligned} A=(A−6E)+6E= −2222−2−22−2−2 + 666 = 42224−22−24
相关文章:

运用谱分解定理反求实对称矩阵
文章目录 谱分解定理定理的运用 谱分解定理 设三阶实对称矩阵 A A A,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3,对应的单位化特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α…...

Qt——Qt工作原理:事件驱动、信号与槽机制
Qt工作原理:事件驱动、信号与槽机制 Qt作为一个现代的GUI(图形用户界面)框架,采用了事件驱动的编程范式,并引入了信号与槽机制,以实现高度交互和松耦合的程序设计。下面详细解释了相关概念,以及…...

find ./* -type d -empty -exec touch {}/.gitkeep \;
这是一个 Linux 下的 find 命令,用于在所有空目录中创建 .gitkeep 文件。让我们来分解一下这个命令做了什么:- find ./* : 在当前目录及其子目录中查找。 -type d : 只查找目录类型的文件。 -empty : 只找出那些空的目…...

计算机行业前景展望
计算机行业的前景展望是非常广阔的。随着技术的快速发展和应用领域的不断拓展,计算机行业将继续扮演着重要的角色。以下是一些计算机行业前景的关键方面: 人工智能(AI)和机器学习(ML):AI和ML技术…...
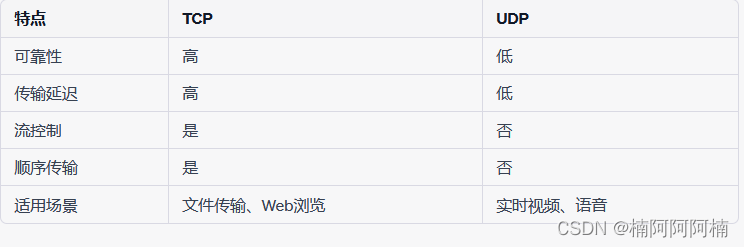
TCP/UDP原理
文章目录 一、端口1. 端口的定义和作用2.服务端和客户端的区别3.常见的知名端口号有 二、TCP的原理1.TCP头部封装格式2.TCP可靠性机制三次握手确认机制四次挥手RST结束连接窗口机制 3.完整性校验4.TCP特征5.TCP的适用场景 三、UDP的原理1.UDP头部封装格式2.UDP特征3.UDP的适用场…...
操作符算数转换题
目录 1.交换两个变量(不创建临时变量) 2.统计二进制中1的个数 3.打印整数二进制的奇数位和偶数位 4.求两个数二进制中不同位的个数 5.【一维数组】有序序列合并 6.获得月份天数 7.变种水仙花数 8.选择题总结tips 这篇博文主要分享操作符&算…...

Centos7 安装 Docker
2年前写过一篇安装Docker的文档记录,当时安装有些麻烦,现在安装docker就非常容易了,而且安装完docker,自动也安装了docker compose,不用再去执行指令单独安装docker compose了,所以现在再记录一下ÿ…...

Java虚拟机内部组成
1、栈区 public class Math {public int compute(){//一个方法对应一块栈帧内存区域int a l;int b 2;int c (a b)*10;return c; } public static void main(String[] args){Math math new, Math() ;math.compute() ;System.out.println("test");}} 栈是先进后出…...
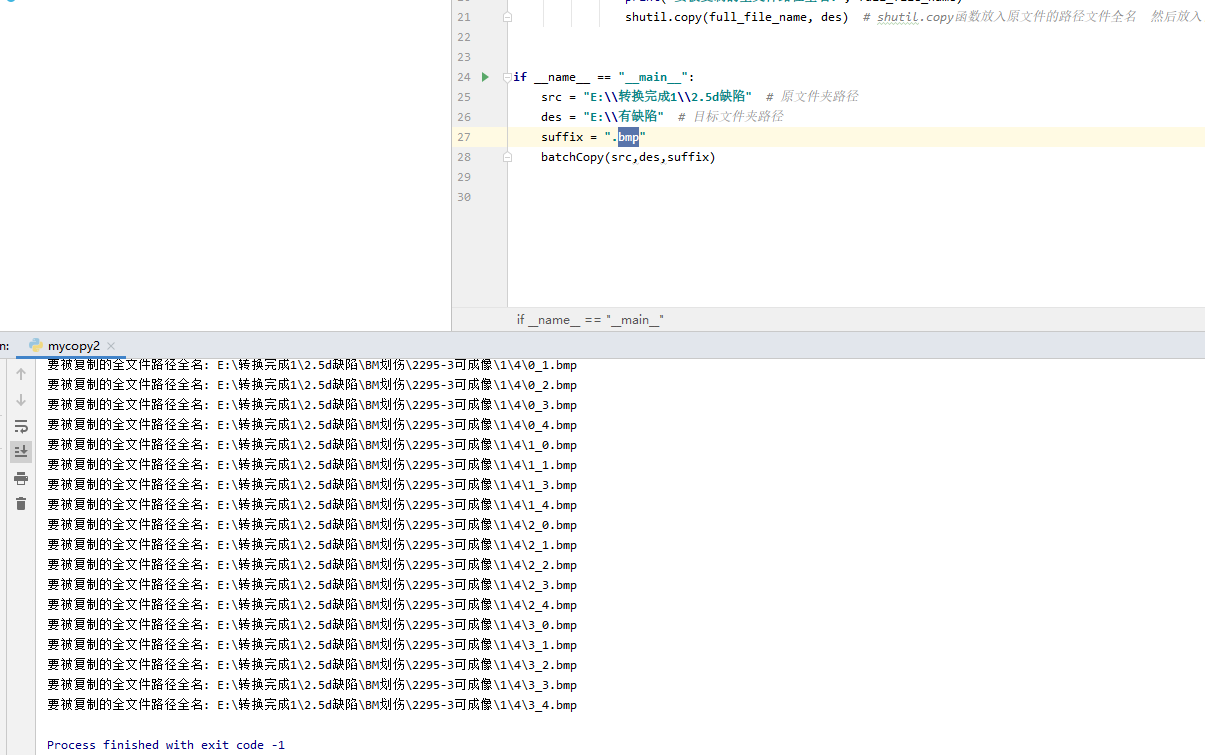
python遍历文件夹下的所有子文件夹,并将指定的文件复制到指定目录
python遍历文件夹下的所有子文件夹,并将指定的文件复制到指定目录 需求复制单个文件夹遍历所有子文件夹中的文件,并复制代码封装 需求 在1文件夹中有1,2两个文件夹 将这两个文件夹中的文件复制到 after_copy中 复制单个文件夹 # coding: ut…...

[golang 流媒体在线直播系统] 1.直播的简单介绍以及借助腾讯云直播实现在线直播
一.直播的简单介绍 1.介绍 直播,应该不陌生,有电视直播、网络主播、游戏直播、体育直播、在线教育直播等等,那么要实现在线直播的话就 必须要有 “ 流媒体在线直播服务器 ”. “流媒体在线直播服务器 ”不仅可以 实现游戏、赛事、电商、媒体、教育等行业的直播, 还可以实现 …...

C# 中操作集合的方法
Add:向集合中添加元素。 List<int> numbers new List<int>(){ 1, 2, 3 }; numbers.Add(4); // numbers 现在为 { 1, 2, 3, 4 }Remove:从集合中移除指定的元素。 List<int> numbers new List<int>(){ 1, 2, 3, 4 }; numbers.Re…...
pytorch学习(8)——现有网络模型的使用以及修改
1 vgg16模型 1.1 vgg16模型的下载 采用torchvision中的vgg16模型,能够实现1000个类型的图像分类,VGG模型在AlexNet的基础上使用3*3小卷积核,增加网络深度,具有很好的泛化能力。 首先下载vgg16模型,python代码如下&…...

get和post请求的区别
GET和POST是HTTP请求的两种方法,其区别如下 ① GET请求表示从指定的服务器中获取数据(请求数据),比如查询用户信息;POST请求表示将数据提交到指定的服务器进行处理(发送数据), ② GET请求是一个幂等的请求,一般用于对服务器资源不会产生影响的场景,比如说请求一个网友的…...

extern “C”关键字的作用
目录 概述C和C在函数调用和变量命名等方面的差异示例总结 概述 extern "C"是用于在C中声明使用C语言编写的函数和变量的关键字。C和C在函数调用和变量命名等方面存在一些差异,为了在C代码中正确地使用C语言的函数和变量,需要使用extern "…...

使用ffmpeg截取视频片段
本文将介绍2中使用ffmpeg截取视频的方法 指定截取视频的 开始时间 和 结束时间,进行视频截取指定截取视频的 开始时间 和 截取的秒数,进行视频截取 两种截取方式的命令行如下 截取某一时间段视频 优先使用 ffmpeg -i ./input.mp4 -c:v libx264 -crf…...

Python教程(11)——Python中的字典dict的用法介绍
dict的用法介绍 创建字典访问字典修改字典删除字典字典的相关函数 列表虽然好,但是如果需要快速的数据查找,就必须进行需要遍历,也就是最坏情况需要遍历完一遍才能找到需要的那个数据,时间复杂度是O(n),显然这个速度是…...

三道dfs题
一:1114. 棋盘问题 - AcWing题库 分别枚举行和列,能填的地方就填,dfs就行 #include <iostream> using namespace std;const int N 10; char g[N][N]; int n, k; int res; bool st[N];void dfs(int u, int cnt) // u枚举行 {if(cnt …...
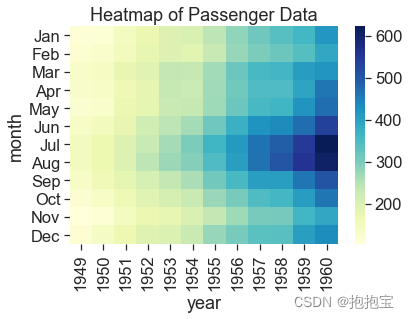
Seaborn数据可视化(四)
目录 1.绘制箱线图 2.绘制小提琴图 3.绘制多面板图 4.绘制等高线图 5.绘制热力图 1.绘制箱线图 import seaborn as sns import matplotlib.pyplot as plt # 加载示例数据(例如,使用seaborn自带的数据集) tips sns.load_dataset("t…...

kubernetes deploy standalone mysql demo
kubernetes 集群内部署 单节点 mysql ansible all -m shell -a "mkdir -p /mnt/mysql/data"cat mysql-pv-pvc.yaml apiVersion: v1 kind: PersistentVolume metadata:name: mysql-pv-volumelabels:type: local spec:storageClassName: manualcapacity:storage: 5Gi…...
)
【Map】Map集合有序与无序测试案例:HashMap,TreeMap,LinkedHashMap(121)
简单介绍常用的三种Map:不足之处,欢迎指正! HashMap:put数据是无序的; TreeMap:key值按一定的顺序排序;数字做key,put数据是有序,非数字字符串做key,put数据…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
