当前位置：首页 > news >正文

部署你自己的导航站-dashy

news 2025/9/18 16:49:38

现在每天要访问的网页都太多了，尽管chrome非常好用，有强大的标签系统。但是总觉的少了点什么。
今天我就来分享一个开源的导航网站系统 dashy。这是一个国外的大佬的开源项目
github地址如下：https://github.com/Lissy93/dashy

来简单说一下为什么来分享这个项目

支持多页面管理
完全免费和开源
安装简单，支持docker
页面支持中文！

那么接下来我们采用docker的方式进行安装，一条命令即可。

ssh连接到你的终端
输入命令 docker run -d -p 4000:80 lissy93/dashy 来拉去并且启动容器
前台访问 http://ip:4000 就可以看到前台页面已经启动了。
我们首先把语言改成中文
点击右上角编辑页面，然后新增section
我在这里新建了一个section。名字为搜索网站，你可以设置这个分区的图标（需要图片地址），以及排序方式，还有行和列等配置。
新建好分区之后，我们就可以新建item了。
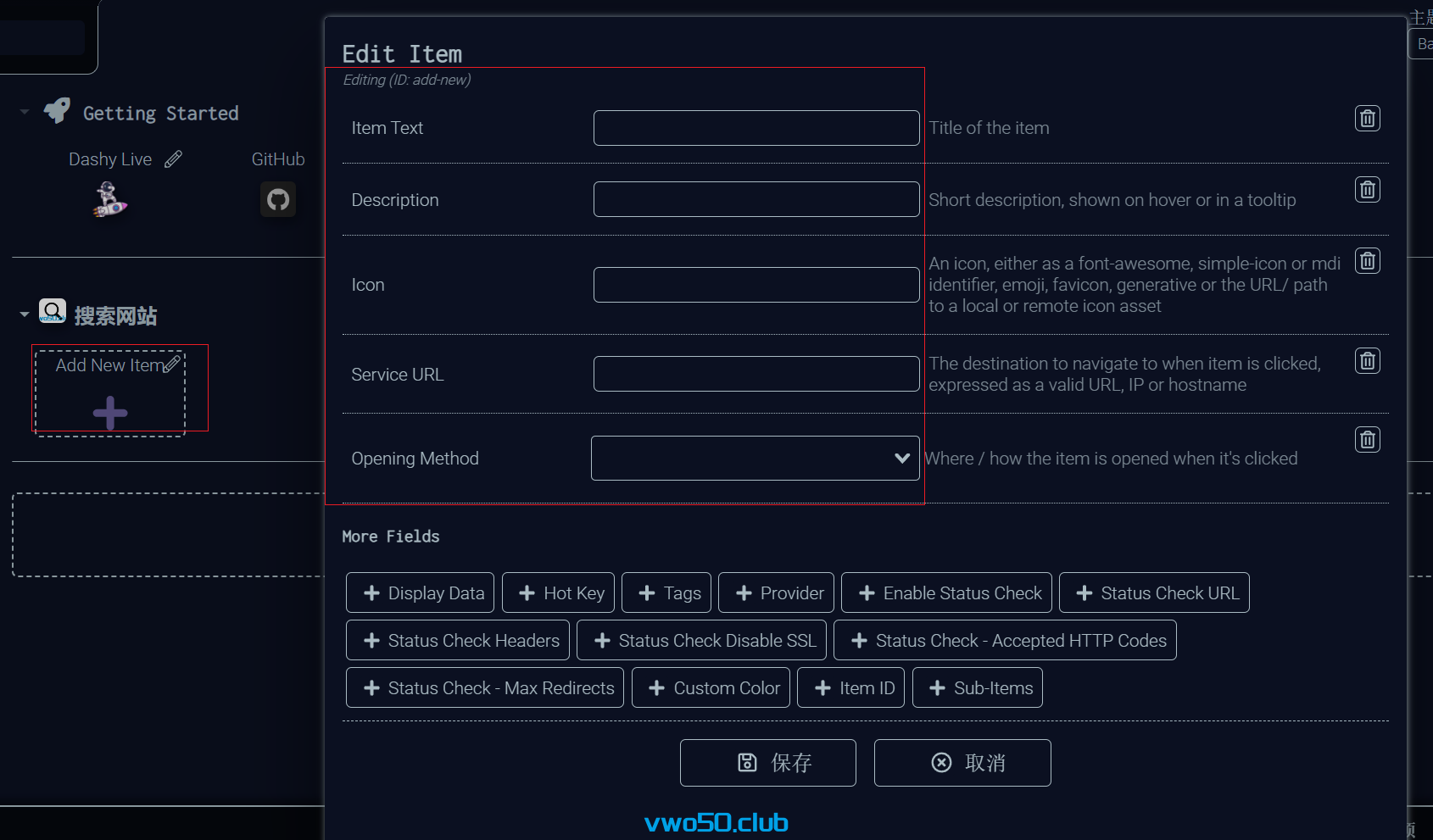
我这里以百度举例子。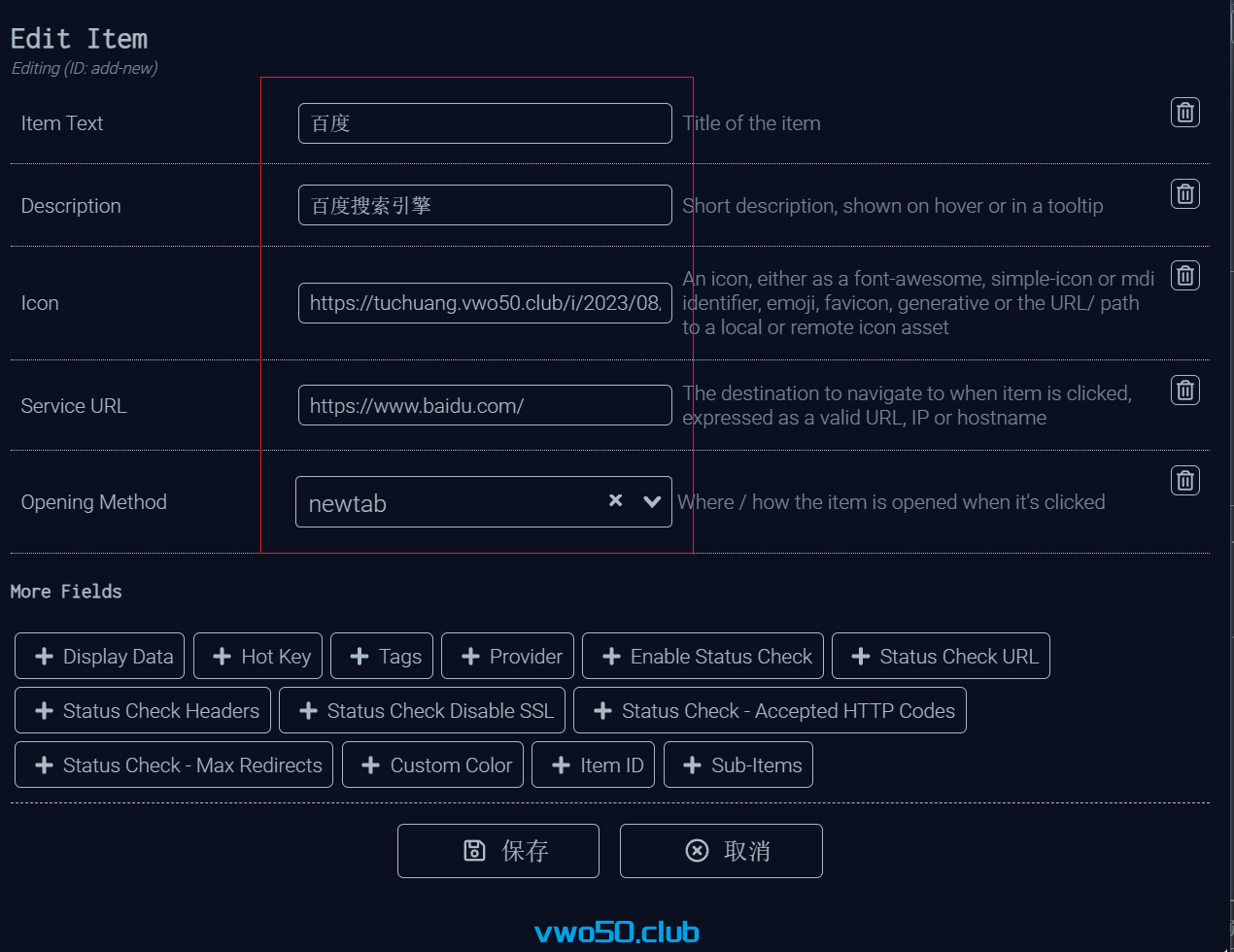创建好之后我们保存看看效果。然后又添加了google 和bing。他们的icon我随便添加的。所以看起来不美观。
这里再说一下它的其他功能把。大家可以自行探索
主题和布局支持修改，而且主题支持编辑，主题很丰富
支持云端备份和同步
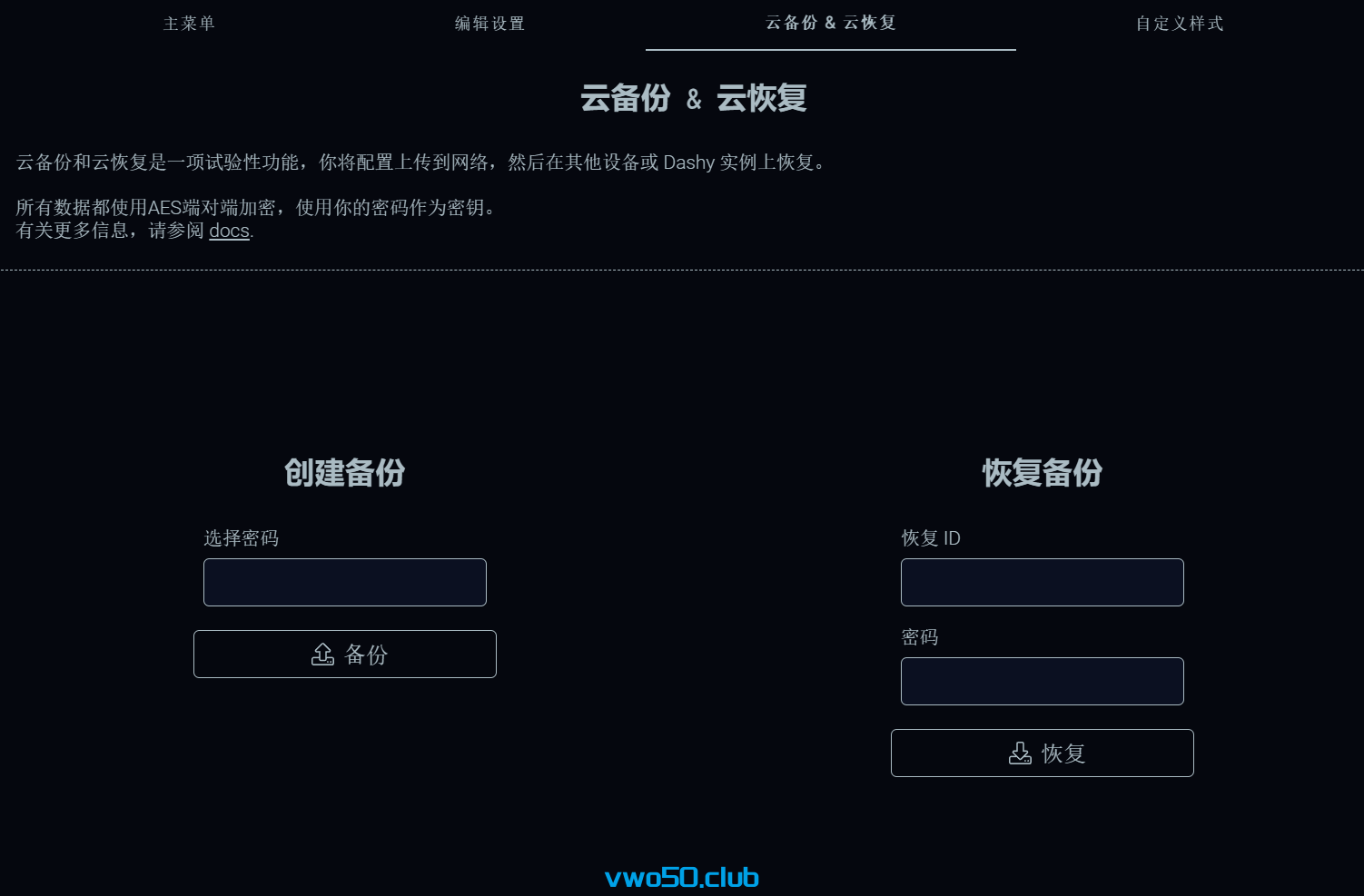
11.支持搜索和自定义样式

总体来看，这个导航站还是不错的，很多东西都支持自定义。感兴趣的可以自己去装一下。然后也是设置反向代理后绑定域名，就
可以拥有自己的导航站了。

部署你自己的导航站-dashy

现在每天要访问的网页都太多了，尽管chrome非常好用，有强大的标签系统。但是总觉的少了点什么。今天我就来分享一个开源的导航网站系统 dashy。这是一个国外的大佬的开源项目 github地址如下：https://github.com/Lissy93/dashy 来简单说一下…...

编程日记 2023/9/1 1:45:53

运用谱分解定理反求实对称矩阵

文章目录谱分解定理定理的运用谱分解定理设三阶实对称矩阵 A A A，若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3，对应的单位化特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α…...

编程日记 2023/9/1 1:44:50

Qt——Qt工作原理：事件驱动、信号与槽机制

Qt工作原理：事件驱动、信号与槽机制 Qt作为一个现代的GUI（图形用户界面）框架，采用了事件驱动的编程范式，并引入了信号与槽机制，以实现高度交互和松耦合的程序设计。下面详细解释了相关概念，以及…...

编程日记 2023/9/1 1:43:49

find ./* -type d -empty -exec touch {}/.gitkeep \；

这是一个 Linux 下的 find 命令，用于在所有空目录中创建 .gitkeep 文件。让我们来分解一下这个命令做了什么：- find ./* ： 在当前目录及其子目录中查找。 -type d ： 只查找目录类型的文件。 -empty ： 只找出那些空的目…...

编程日记 2023/9/1 1:42:46

计算机行业前景展望

计算机行业的前景展望是非常广阔的。随着技术的快速发展和应用领域的不断拓展，计算机行业将继续扮演着重要的角色。以下是一些计算机行业前景的关键方面： 人工智能（AI）和机器学习（ML）：AI和ML技术…...

编程日记 2023/9/1 1:41:44

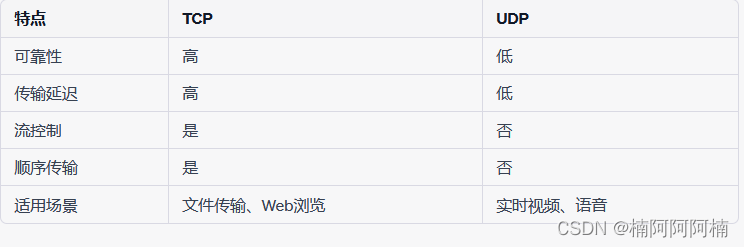
TCP/UDP原理

文章目录一、端口1. 端口的定义和作用2.服务端和客户端的区别3.常见的知名端口号有二、TCP的原理1.TCP头部封装格式2.TCP可靠性机制三次握手确认机制四次挥手RST结束连接窗口机制 3.完整性校验4.TCP特征5.TCP的适用场景三、UDP的原理1.UDP头部封装格式2.UDP特征3.UDP的适用场…...

编程日记 2023/9/1 1:40:42

操作符算数转换题

目录 1.交换两个变量（不创建临时变量） 2.统计二进制中1的个数 3.打印整数二进制的奇数位和偶数位 4.求两个数二进制中不同位的个数 5.【一维数组】有序序列合并 6.获得月份天数 7.变种水仙花数 8.选择题总结tips 这篇博文主要分享操作符&算…...

编程日记 2023/9/1 1:39:41

Centos7 安装 Docker

2年前写过一篇安装Docker的文档记录，当时安装有些麻烦，现在安装docker就非常容易了，而且安装完docker，自动也安装了docker compose，不用再去执行指令单独安装docker compose了，所以现在再记录一下&#xff…...

编程日记 2023/9/1 1:38:39

1、栈区 public class Math {public int compute(){//一个方法对应一块栈帧内存区域int a l;int b 2;int c (a b)*10;return c; } public static void main(String[] args){Math math new, Math() ;math.compute() ;System.out.println("test");}} 栈是先进后出…...

编程日记 2023/9/1 1:37:38

python遍历文件夹下的所有子文件夹，并将指定的文件复制到指定目录

python遍历文件夹下的所有子文件夹，并将指定的文件复制到指定目录需求复制单个文件夹遍历所有子文件夹中的文件，并复制代码封装需求在1文件夹中有1，2两个文件夹将这两个文件夹中的文件复制到 after_copy中复制单个文件夹 # coding: ut…...

编程日记 2023/9/1 1:36:37

[golang 流媒体在线直播系统] 1.直播的简单介绍以及借助腾讯云直播实现在线直播

一.直播的简单介绍 1.介绍直播，应该不陌生，有电视直播、网络主播、游戏直播、体育直播、在线教育直播等等,那么要实现在线直播的话就必须要有 “ 流媒体在线直播服务器 ”. “流媒体在线直播服务器 ”不仅可以实现游戏、赛事、电商、媒体、教育等行业的直播, 还可以实现 …...

编程日记 2023/9/1 1:35:36

C# 中操作集合的方法

Add：向集合中添加元素。 List<int> numbers new List<int>(){ 1, 2, 3 }; numbers.Add(4); // numbers 现在为 { 1, 2, 3, 4 }Remove：从集合中移除指定的元素。 List<int> numbers new List<int>(){ 1, 2, 3, 4 }; numbers.Re…...

编程日记 2023/9/1 1:34:35

pytorch学习（8）——现有网络模型的使用以及修改

1 vgg16模型 1.1 vgg16模型的下载采用torchvision中的vgg16模型，能够实现1000个类型的图像分类，VGG模型在AlexNet的基础上使用3*3小卷积核，增加网络深度，具有很好的泛化能力。首先下载vgg16模型，python代码如下&…...

编程日记 2023/9/1 1:33:34

get和post请求的区别

GET和POST是HTTP请求的两种方法，其区别如下 ① GET请求表示从指定的服务器中获取数据(请求数据)，比如查询用户信息；POST请求表示将数据提交到指定的服务器进行处理(发送数据)， ② GET请求是一个幂等的请求，一般用于对服务器资源不会产生影响的场景，比如说请求一个网友的…...

编程日记 2023/9/1 1:32:32

extern “C”关键字的作用

目录概述C和C在函数调用和变量命名等方面的差异示例总结概述 extern "C"是用于在C中声明使用C语言编写的函数和变量的关键字。C和C在函数调用和变量命名等方面存在一些差异，为了在C代码中正确地使用C语言的函数和变量，需要使用extern "…...

编程日记 2023/9/1 1:31:30

使用ffmpeg截取视频片段

本文将介绍2中使用ffmpeg截取视频的方法指定截取视频的开始时间和结束时间，进行视频截取指定截取视频的开始时间和截取的秒数，进行视频截取两种截取方式的命令行如下截取某一时间段视频优先使用 ffmpeg -i ./input.mp4 -c:v libx264 -crf…...

编程日记 2023/9/1 1:30:29

Python教程(11)——Python中的字典dict的用法介绍

dict的用法介绍创建字典访问字典修改字典删除字典字典的相关函数列表虽然好，但是如果需要快速的数据查找，就必须进行需要遍历，也就是最坏情况需要遍历完一遍才能找到需要的那个数据，时间复杂度是O(n)，显然这个速度是…...

编程日记 2023/9/1 1:29:28

三道dfs题

一：1114. 棋盘问题 - AcWing题库分别枚举行和列，能填的地方就填，dfs就行 #include <iostream> using namespace std;const int N 10; char g[N][N]; int n, k; int res; bool st[N];void dfs(int u, int cnt) // u枚举行 {if(cnt …...

编程日记 2023/9/1 1:28:27

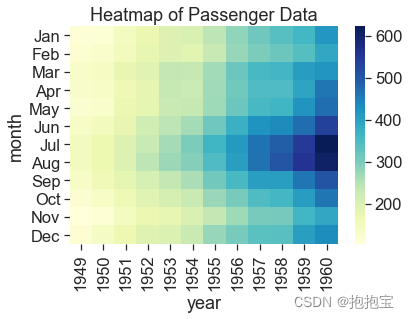
Seaborn数据可视化（四）

目录 1.绘制箱线图 2.绘制小提琴图 3.绘制多面板图 4.绘制等高线图 5.绘制热力图 1.绘制箱线图 import seaborn as sns import matplotlib.pyplot as plt # 加载示例数据（例如，使用seaborn自带的数据集） tips sns.load_dataset("t…...

编程日记 2023/9/1 1:27:26

kubernetes deploy standalone mysql demo

kubernetes 集群内部署单节点 mysql ansible all -m shell -a "mkdir -p /mnt/mysql/data"cat mysql-pv-pvc.yaml apiVersion: v1 kind: PersistentVolume metadata:name: mysql-pv-volumelabels:type: local spec:storageClassName: manualcapacity:storage: 5Gi…...

编程日记 2023/9/1 1:26:25