【月度刷题计划同款】常规状压 DP 启发式搜索
题目描述
这是 LeetCode 上的 「1879. 两个数组最小的异或值之和」 ,难度为 「困难」。
Tag : 「状压 DP」、「动态规划」、「启发式搜索」
给你两个整数数组 nums1 和 nums2,它们长度都为 n。
两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) (下标从 0 开始)。
比方说,[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4。
请你将 nums2 中的元素重新排列,使得异或值之和最小 。
请你返回重新排列之后的 异或值之和 。
示例 1:
输入:nums1 = [1,2], nums2 = [2,3]
输出:2
解释:将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2 。
示例 2:
输入:nums1 = [1,0,3], nums2 = [5,3,4]
输出:8
解释:将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8 。
提示:
状压 DP
这是一道「状压 DP」模板题。
为了方便,我们令下标从 开始。
「定义 为考虑前 个元素,且对 nums2 的使用情况为 时的最小异或值」。其中 是一个长度为 的二进制数:若 中的第 位为 ,说明 nums2[k] 已被使用;若 中的第 位为 ,说明 nums2[k] 未被使用。
起始时,只有 ,其余均为无穷大 INF。 含义为在不考虑任何数,对 nums2 没有任何占用情况时,最小异或值为 。最终 即为答案。
不失一般性考虑 该如何转移,可以以 nums1[i] 是与哪个 nums2[j] 进行配对作为切入点:
-
由于总共考虑了前 个成员,因此 中 的数量必然为 ,否则 就不是一个合法状态,跳过转移
-
枚举
nums1[i]是与哪一个nums2[j]进行配对的,且枚举的 需满足在 中的第 位值为 ,若满足则有
其中 prev 为将 中的第 位进行置零后的二进制数,即 prev = s ^ (1 << j),符号 ⊕ 代表异或操作。
Java 代码:
class Solution {
public int minimumXORSum(int[] nums1, int[] nums2) {
int n = nums1.length, mask = 1 << n, INF = 0x3f3f3f3f;
int[][] f = new int[n + 10][mask];
for (int i = 0; i <= n; i++) Arrays.fill(f[i], INF);
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int s = 0; s < mask; s++) {
if (getCnt(s, n) != i) continue;
for (int j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) == 0) continue;
f[i][s] = Math.min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
}
int getCnt(int s, int n) {
int ans = 0;
for (int i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
}
}
C++ 代码:
class Solution {
public:
int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), mask = 1 << n, INF = 0x3f3f3f3f;
vector<vector<int>> f(n + 10, vector<int>(mask, INF));
f[0][0] = 0;
auto getCnt = [&](int s, int n) {
int ans = 0;
for (int i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
};
for (int i = 1; i <= n; i++) {
for (int s = 0; s < mask; s++) {
if (getCnt(s, n) != i) continue;
for (int j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) == 0) continue;
f[i][s] = min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
}
};
Python 代码:
class Solution:
def minimumXORSum(self, nums1: List[int], nums2: List[int]) -> int:
n, mask, INF = len(nums1), 1 << len(nums1), 0x3f3f3f3f
f = [[INF] * mask for _ in range(n + 10)]
f[0][0] = 0
for i in range(1, n + 1):
for s in range(mask):
if sum([1 for i in range(n) if (s >> i) & 1]) != i:
continue
for j in range(1, n + 1):
if ((s >> (j - 1)) & 1) == 0:
continue
f[i][s] = min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]))
return f[n][mask - 1]
TypeScript 代码:
function minimumXORSum(nums1: number[], nums2: number[]): number {
const n = nums1.length, mask = 1 << n, INF = 0x3f3f3f3f;
const f: number[][] = new Array(n + 10).fill([]).map(() => new Array(mask).fill(INF));
f[0][0] = 0;
const getCnt = (s: number, n: number): number => {
let ans = 0;
for (let i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
};
for (let i = 1; i <= n; i++) {
for (let s = 0; s < mask; s++) {
if (getCnt(s, n) !== i) continue;
for (let j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) === 0) continue;
f[i][s] = Math.min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
};
-
时间复杂度: -
空间复杂度:
模拟退火
事实上,这道题还能使用「模拟退火」进行求解。
由于我们可以无限次对 nums2 进行打乱互换,先来思考如何衡量一个 nums2 排列的“好坏”。
一个简单的方式:固定计算 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) 作为衡量当前 nums2 的得分,得分越小,当前的 nums2 排列越好。
迭代开始前先对 nums2 进行一次随机打乱,随后每个回合随机选择 nums2 的两个成员进行互换,并比较互换前后的得分情况,若互换后变好,那么保留该互换操作;若变差,则以一定概率进行重置(重新换回来)。
重复迭代多次,使用一个全局变量 ans 保存下最小异或值之和。
即「模拟退火」的单次迭代基本流程:
-
随机选择两个下标,计算「交换下标元素前对应序列的得分」&「交换下标元素后对应序列的得分」 -
如果温度下降(交换后的序列更优),进入下一次迭代 -
如果温度上升(交换前的序列更优),以「一定的概率」恢复现场(再交换回来)
❝对于一个能够运用模拟退火求解的问题,最核心的是如何实现
❞calc方法(即如何定义一个具体方案的得分),其余均为模板内容。
Java 代码(2023/08/23 可过):
class Solution {
int N = 400;
double hi = 1e5, lo = 1e-5, fa = 0.90;
Random random = new Random(20230823);
void swap(int[] n, int a, int b) {
int c = n[a];
n[a] = n[b];
n[b] = c;
}
int calc() {
int res = 0;
for (int i = 0; i < n; i++) res += n1[i] ^ n2[i];
ans = Math.min(ans, res);
return res;
}
void shuffle(int[] nums) {
for (int i = n; i > 0; i--) swap(nums, random.nextInt(i), i - 1);
}
void sa() {
shuffle(n2);
for (double t = hi; t > lo; t *= fa) {
int a = random.nextInt(n), b = random.nextInt(n);
int prev = calc();
swap(n2, a, b);
int cur = calc();
int diff = cur - prev;
if (Math.log(diff / t) >= random.nextDouble()) swap(n2, a, b);
}
}
int[] n1, n2;
int n;
int ans = Integer.MAX_VALUE;
public int minimumXORSum(int[] nums1, int[] nums2) {
n1 = nums1; n2 = nums2;
n = n1.length;
while (N-- > 0) sa();
return ans;
}
}
-
时间复杂度:启发式搜索不讨论时空复杂度 -
空间复杂度:启发式搜索不讨论时空复杂度
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1879 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:

【月度刷题计划同款】常规状压 DP 启发式搜索
题目描述 这是 LeetCode 上的 「1879. 两个数组最小的异或值之和」 ,难度为 「困难」。 Tag : 「状压 DP」、「动态规划」、「启发式搜索」 给你两个整数数组 nums1 和 nums2,它们长度都为 n。 两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) (nums…...
C#: Json序列化和反序列化,集合为什么多出来一些元素?
如下面的例子,很容易看出问题: 如果类本身的无参构造函数, 就添加了一些元素,序列化,再反序列化,会导致元素增加。 如果要避免,必须添加: new JsonSerializerSettings() { Object…...

Docker教程-centos快速安装和配置Docker
# step 1: 安装必要的一些系统工具 sudo yum install -y yum-utils device-mapper-persistent-data lvm2# Step 2: 添加软件源信息 sudo yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo# Step 3: 更新并安装 Docker-CE sudo …...

three.js(四):react + three.js
绘制多个立方体 1.搭建reactts 项目 npx create-react-app basics-demo --template typescriptreactts 的用法可参考此链接: https://react-typescript-cheatsheet.netlify.app/docs/basic/setup 2.安装three依赖 npm install three types/three --save3.安装路…...
IDEA全局统一设置Maven
原来每次打开新建的项目都需要经过 File-> Settings 重新配置maven,这样很不爽 然而经过 File-> New Projects Setup -> Settings for New Projects 后,再如上图配置后就全局设置好了...
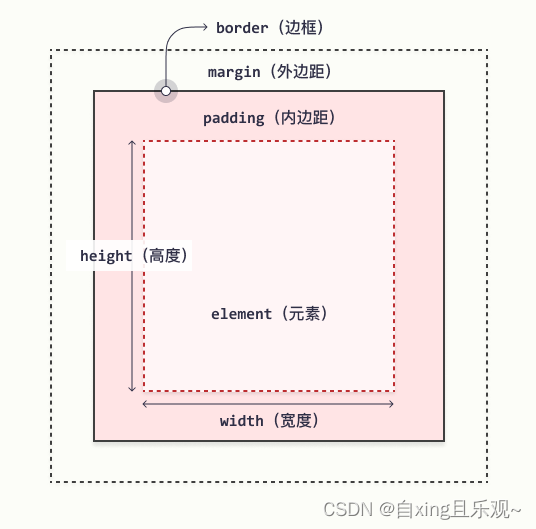
CSS中的margin与padding
目录 一、margin 1.概念及作用 2.基本语法 3.margin的用法 二、padding 1.介绍 2.基本语法及要求 3. 用法 4.内边距和元素宽度 讲这些之前,先看一张图,便于理解 一、margin 1.概念及作用 CSS margin 属性用于在任何定义的边框之外,…...

匿名内部类、Lambda、方法引用 的总结
在今天的项目中看到这样一行代码 Integer syncCount consumer.consumerInfo( Collections.singletonList(KafkaTopicConst.Event_BMS_SYSLOG_ROLE),consumer::handle); 直接傻眼,无法理解consumer::handle这种用法,因此总结如下 consumer::handle这种写…...

本地docker registry 搭建
#!/bin/bash DOCKER_REGISTRY_ROOT/data0/docker/registry DOMAINexample.host.com #生成证书:https://goharbor.io/docs/2.6.0/install-config/configure-https/ mkdir $DOCKER_REGISTRY_ROOT/certs cd $DOCKER_REGISTRY_ROOT/certs openssl genrsa -out ca.key 40…...

阿里云将关停代销业务
我是卢松松,点点上面的头像,欢迎关注我哦! 阿里云自从逐渐分拆独立之后,做了很多调整。最近它又做了一个大动作:据DoNews消息,阿里云将会在今年9月30日之前,全面关停代销业务。 这件事实际上…...
【ES6】JavaScript的Proxy:理解并实现高级代理功能
在JavaScript中,Proxy是一种能够拦截对对象的读取、设置等操作的机制。它们提供了一种方式,可以在执行基本操作之前或之后,对这些操作进行自定义处理。这种功能在许多高级编程场景中非常有用,比如实现数据验证、日志记录、权限控制…...
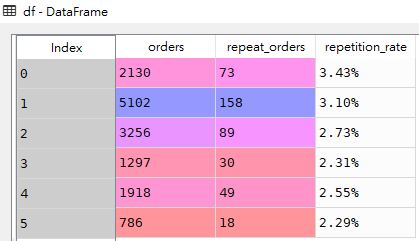
[Pandas] 求百分比并添加百分(%)号
导入数据 import pandas as pddf pd.DataFrame(data{orders: [2130,5102,3256,1297,1918,786],repeat_orders: [73,158,89,30,49,18]}) df df[repetition_rate] df[repeat_orders] / df[orders] df df[repetition_rate] df[repetition_rate].apply(lambda x: format(x, .2…...

《算法竞赛·快冲300题》每日一题:“凑二十四”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 凑…...

git reset --hard HEAD
git reset --hard HEAD 是用于将你的工作目录重置回最后一次提交状态的命令。- git reset 是 git 的一个命令,用于重置你当前的 HEAD 到指定的状态。 --hard 标志告诉 git 要完全重置工作目录和暂存区,去匹配最后一次提交。在这个过程中,所有…...
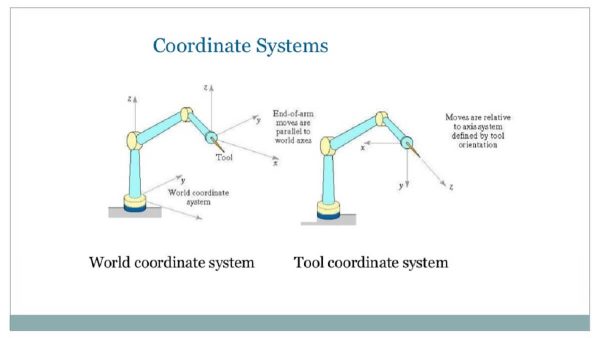
机器人编程怎么入门?
机器人已经在我们中间存在了二三十年。如今,机器人在我们的文化中比以往任何时候都更加根深蒂固。大多数机器人机器用于各种装配线,或在世界各地的矿山或工业设施中执行密集的物理操作。 还有一些家用机器人,工程师正在对机器人进行编程&…...

广州华锐互动:VR垃圾分类虚拟科普系统让学习过程更加丰富有趣
在我们的日常生活中,垃圾分类已成为一项重要的公民责任。然而,由于缺乏对垃圾分类的深入理解和相关知识,许多人在实践中往往感到困惑和挫败。为了解决这个问题,一种创新的解决方案应运而生:垃圾分类VR虚拟仿真教学系统…...

手机盖板IR油墨透光率检测仪T03
手机盖板作为手机最外层玻璃面板,其加工一般有落料、倒边、抛光、镀膜、丝印等多道加工工序组成,其中任何一个工序出现差错,都有可能导致手机盖板产生缺陷,例如漏油、透光、IR孔不良、视窗划伤、油墨区划伤、內污、边花等…...
:ChatGPT 提问设计)
ChatGPT⼊门到精通(6):ChatGPT 提问设计
前⾔ 学会提问就是为了让AI给出⾼质量的答案。 你所学到的技能⼀切为了⽣成⾼质量的答案。 本教程适合:普通ChatGPT的⽤户、专业prompt⼯程师 你将收获:prompt 技巧的全⾯指导 、prompt⼯程师必备技能、prompt技术⼯程⾼质量答 案完全指南 提⽰词 Prom…...

如何使用 Tailwind CSS 设计高级自定义动画
使用Tailwind CSS掌握动画技术,为用户带来难忘的体验 开篇 动画已经成为网页设计的重要组成部分,使开发人员能够创建引人入胜和互动的用户体验。 Tailwind CSS,一款流行的实用型CSS框架,提供了一套强大的工具,可以轻松…...
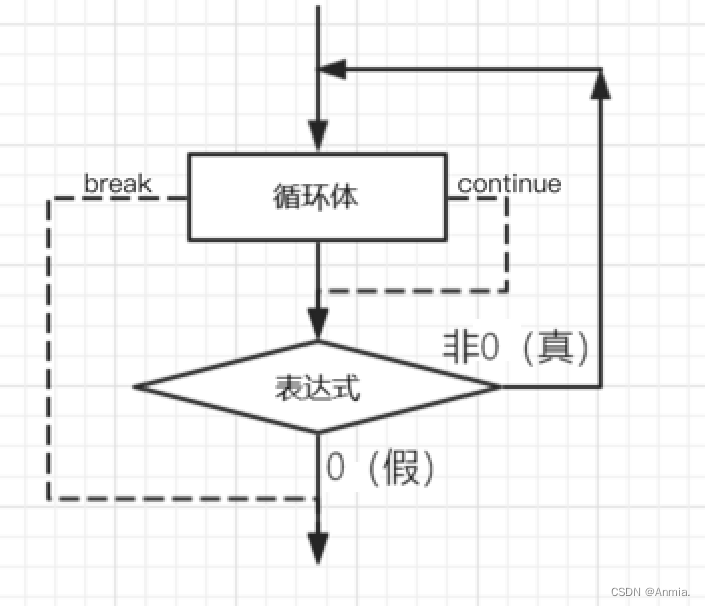
【C语言】循环语句详解
✨个人主页: Anmia.🎉所属专栏: C Language 🎃操作环境: Visual Studio 2019 版本 目录 1.什么是循环结构? 2.while循环 while流程图 while语句中的break和continue break continue 3.for循环 for流…...

SpringBoot项目配置文件数据库用户名密码加密
1、需求 在使用SpringBoot开发过程中,会将一些敏感信息配置到SpringBoot项目的配置文件中(不考虑使用配置中心的情况 ),例如数据库的用户名和密码、Redis的密码等。为了保证敏感信息的安全,我们需要将此类数据进行加密配置。 2、操作步骤 …...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
