选择O型圈时要考虑哪些因素?
为您的应用选择正确的O型圈对于确保适当的密封和较佳性能至关重要。O型圈可用的材料和尺寸多种多样,做出正确的选择可能需要知道一些重要的知识点。在本文中,我们将讨论选择O型圈时需要考虑的一些关键因素。
1、材料兼容性:先要考虑的因素是O型圈材料与应用环境的兼容性。不同的材料对化学品、极端温度和其他因素的耐受程度不同。评估O型圈材料与其所接触的流体、气体和环境条件的兼容性至关重要。这将有助于防止O型圈过早失效或退化。
2、温度范围:另一个需要考虑的关键因素是O型圈的工作温度范围。不同的材料有不同的温度限制。有些材料可以承受极热,而另一些材料在低温下可能会变脆或失去弹性。选择能够承受应用的预期温度范围的O型圈材料非常重要。
3、压力等级:O形圈的压力等级也是一个重要的考虑因素。O型圈需要承受施加在其上的压力而不变形或失效。选择具有适当压力等级的O型圈至关重要,以确保在预期工作条件下实现可靠的密封。
4、尺寸:O形圈的尺寸应与其安装所在的凹槽或外壳相匹配。准确测量凹槽尺寸对于选择正确的O型圈尺寸至关重要。O型圈应紧贴在凹槽中,而不会过度拉伸或压缩。正确的尺寸对于确保有效密封至关重要。
5、应用要求:选择O型圈时请考虑应用的具体要求。应考虑诸如装配和拆卸的频率、润滑的需要以及磨料颗粒的存在等因素。例如,在动态应用中,具有低摩擦和耐磨性的O型圈可能是比较好的选择。
6、质量和认证:确保您选择的O型圈具有高质量并符合行业标准。寻找来自信誉良好的制造商的O型圈,这些制造商遵循严格的质量控制流程。此外,检查O型圈是否有相关认证,例如ISO9001,以确保其可靠性和性能。
7、成本:虽然成本不应是决定因素,但在选择O型圈时考虑您的预算非常重要。不同的材料和尺寸有不同的价格点。然而,平衡成本与质量和性能至关重要,以避免影响密封的有效性。
为您的应用选择O型圈时需要考虑几个因素。材料兼容性、温度范围、压力等级、尺寸、应用要求、质量和成本都是重要的考虑因素。通过仔细评估这些因素,您可以选择合适的O型圈,以提供有效的密封并确保在您的特定应用中实现较佳性能。

相关文章:

选择O型圈时要考虑哪些因素?
为您的应用选择正确的O型圈对于确保适当的密封和较佳性能至关重要。O型圈可用的材料和尺寸多种多样,做出正确的选择可能需要知道一些重要的知识点。在本文中,我们将讨论选择O型圈时需要考虑的一些关键因素。 1、材料兼容性:先要考虑的因素是…...

安全管理中心技术测评要求项
1.系统管理-通过系统管理员进行系统管理操作 1-0/2-2/3-2/4-2 a)对系统管理员进行身份鉴别,只允许其通过特定的命令或操作界面进行系统管理操作,并对这些操作进行审计 b)通过系统管理员对系统的资源和运行进行配置、控制和管理&am…...
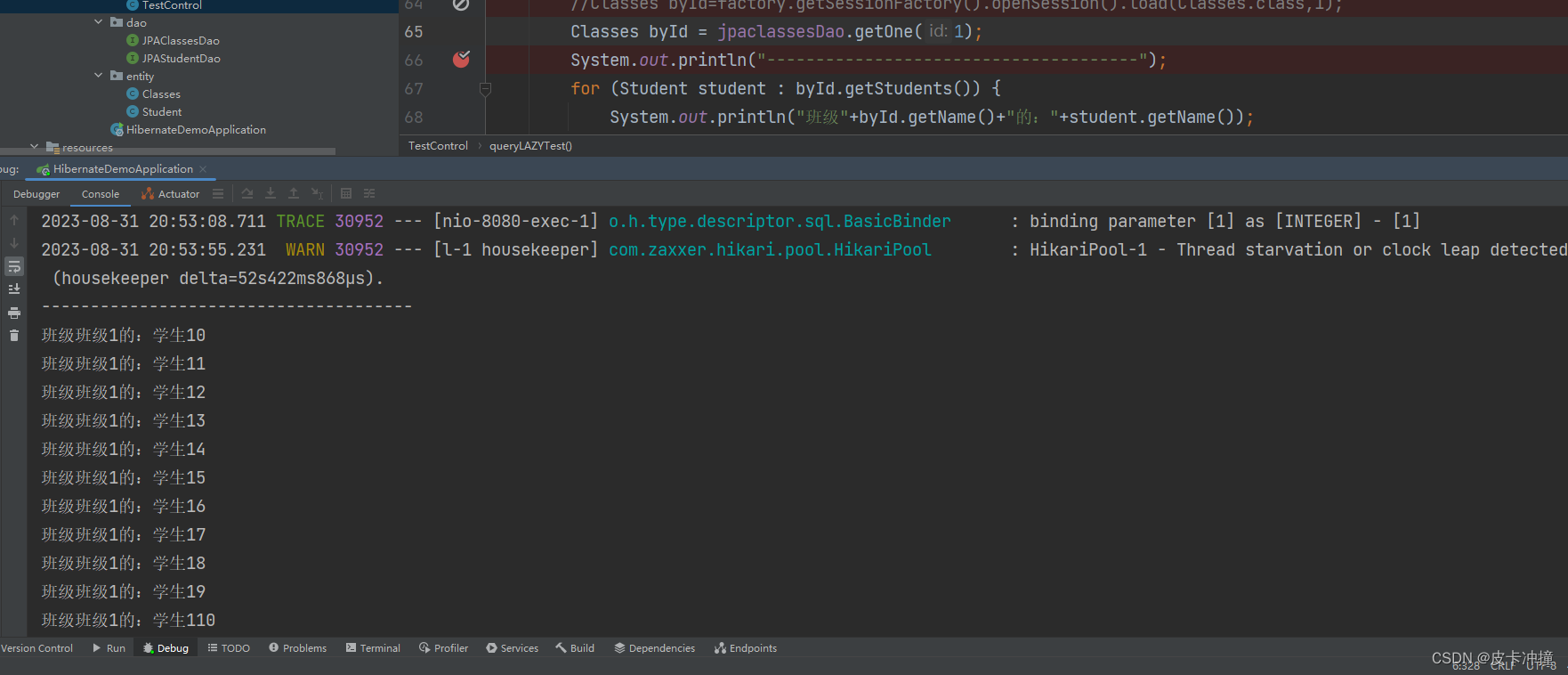
Hibernate(Spring Data)抓取策略
文章目录 示例代码放到最后,使用的是Springboot 项目1. 简介2. Hibernate抓取策略分类2.1 即时加载(Eager Loading)2.2 延迟加载(Lazy Loading)2.3 子查询加载(Subselect Loading)2.4 基于批处理…...
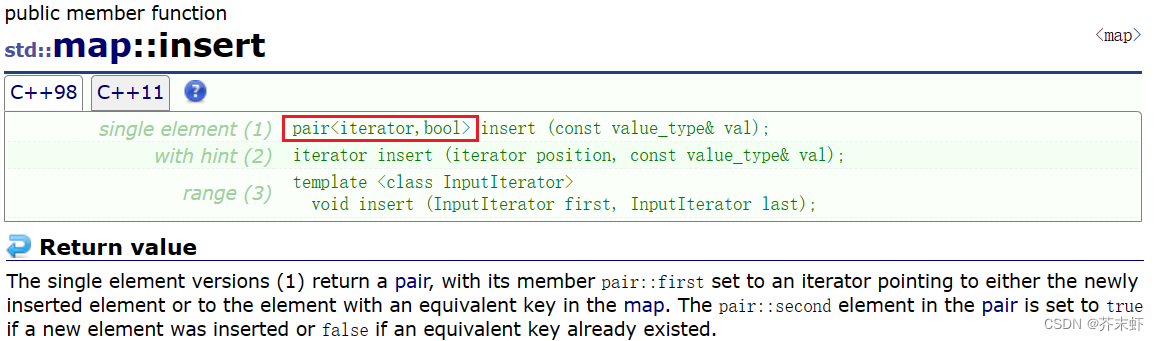
【高阶数据结构】map和set的介绍和使用 {关联式容器;键值对;map和set;multimap和multiset;OJ练习}
map和set的介绍和使用 一、关联式容器 关联式容器和序列式容器是C STL中的两种不同类型的容器。 关联式容器是基于键值对的容器,其中每个元素都有一个唯一的键值,可以通过键值来访问元素。关联式容器包括set、multiset、map和multimap。 序列式容器是…...

系统架构技能之设计模式-单件模式
一、开篇 其实我本来不是打算把系统架构中的一些设计模式单独抽出来讲解的,因为很多的好朋友也比较关注这方面的内容,所以我想通过我理解及平时项目中应用到的一 些常见的设计模式,拿出来给大家做个简单讲解,我这里只是抛砖引玉,…...
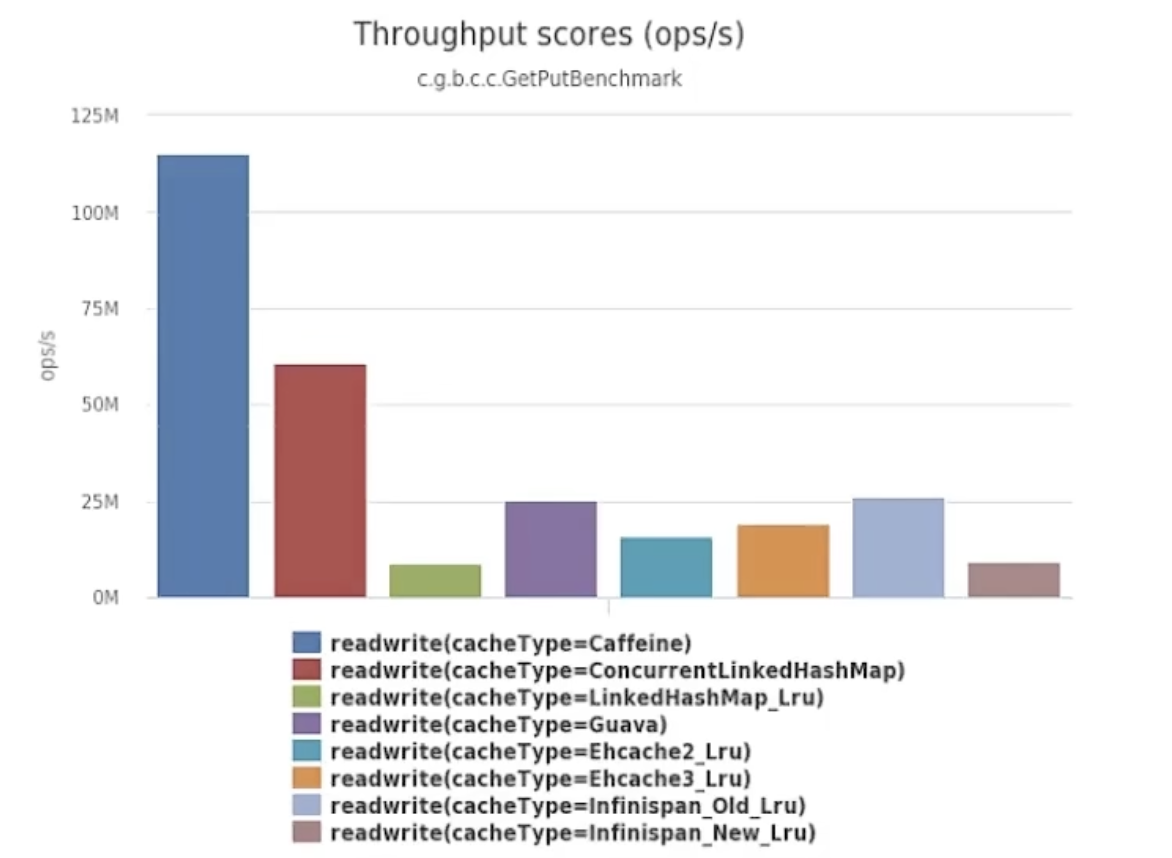
Redis进阶 - JVM进程缓存
原文首更地址,阅读效果更佳! Redis进阶 - JVM进程缓存 | CoderMast编程桅杆https://www.codermast.com/database/redis/redis-advance-jvm-process-cache.html 传统缓存的问题 传统的缓存策略一般是请求到达 Tomcat 后,先查询 Redis &…...

SD-WAN带您告别高成本、单一功能和安全性差
现今,随着企业规模不断扩大和分散办公越来越普遍,企业对于网络的需求也变得越来越高。然而,传统的组网方式面临着很多的问题,比如:成本高、功能单一、安全性差等问题。 传统组网方式有哪些? 传统的组网方式…...

面试必备:揭秘ArrayList和LinkedList,区别、优缺点与使用场景
大家好,我是你们的小米!今天我要跟大家聊一个在面试中经常被问到的热门话题——ArrayList和LinkedList的区别、优缺点以及它们的使用场景。作为程序员,掌握这些知识点不仅可以在面试中脱颖而出,还能帮助我们更好地在项目中选择合适…...
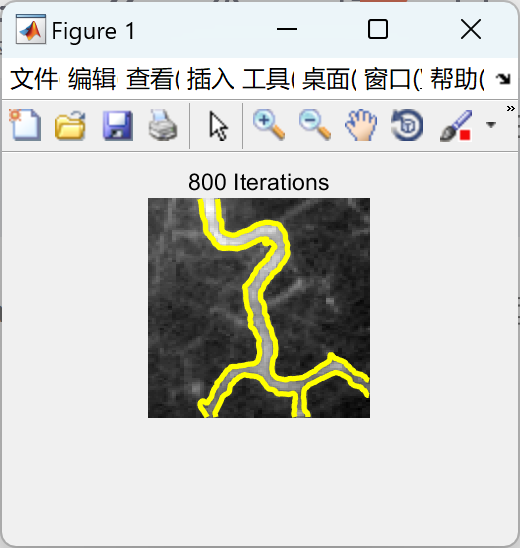
【局部活动轮廓】使用水平集方法实现局部活动轮廓方法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Git 同步远程新的同名分支
背景 因为远程分支的提交记录过多,导致本地的commit内容过大,会产生一些问题: 第一次拉取时间较长占用本地和远程的存储 原因 因为项目已有一些年头,若是每次文件提交比较大,那么占用空间就更大 解决方案 该方案…...

PingCode DevOps 团队:企业CICD流水线可能会遇到的问题及解法
CICD 流水线是指一系列自动化的构建、测试和部署步骤,用于将应用程序从开发到生产环境的过程。在 CICD 流水线中,每个步骤都是自动化的,并且在完成后会触发下一个步骤的执行。 CICD 的价值 CICD 流水线可以帮助团队更快地交付产品ÿ…...
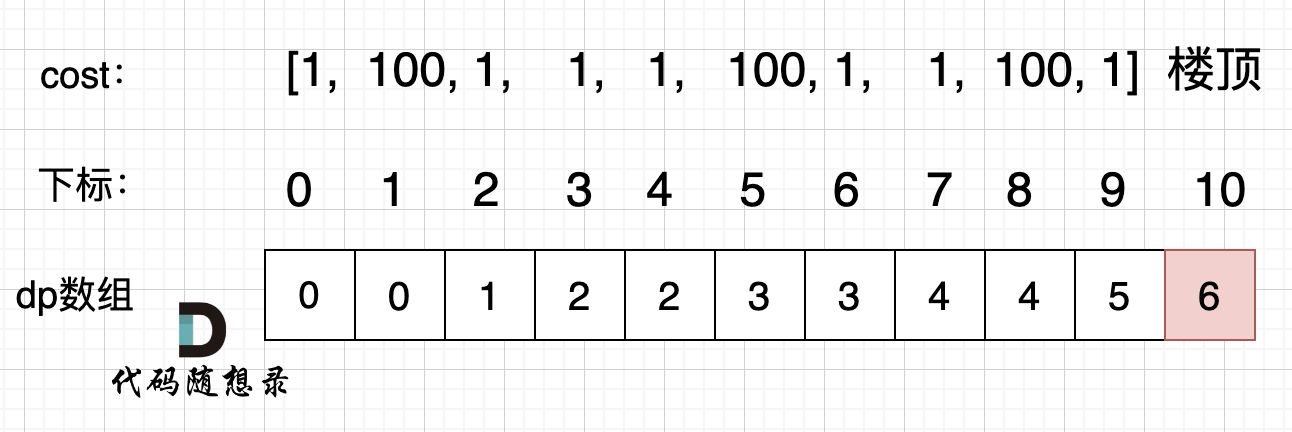
【LeetCode题目详解】第九章 动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯 (day38补)
本文章代码以c为例! 一、力扣第509题:斐波那契数 题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:…...
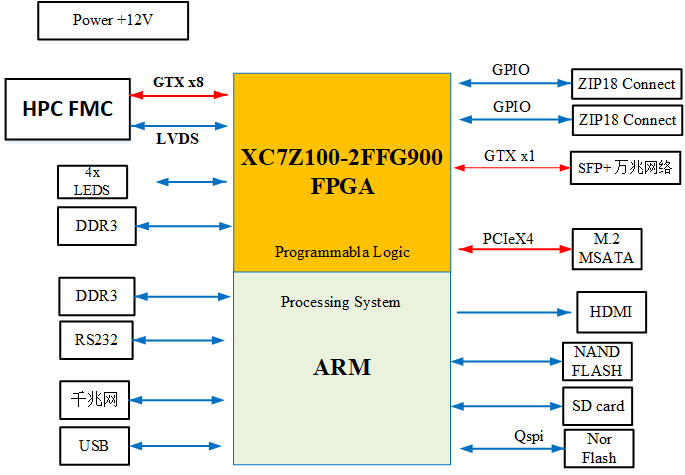
图像处理 信号处理板 设计原理图:367-基于zynq XC7Z100 FMC接口通用计算平台
基于zynq XC7Z100 FMC接口通用计算平台 一、板卡概述 板卡由SoC XC7Z100-2FFG900I芯片来完成卡主控及数字信号处理,XC7Z100内部集成了两个ARM Cortex-A9核和一个kintex 7的FPGA,通过PL端FPGA扩展FMC、光纤、IO等接口,PS端ARM扩展网络、USB、R…...
的七种用法)
PHP中header()的七种用法
我们在实际开发中经常使用header()实现一些功能,这篇文章介绍关于header()的7中用法,需要的伙伴的开参考一下。 PHP header()的7中用法: 1、跳转页面 可以使用header()实现跳转页面功能。 header(Location:.$url); // $url 跳转页面的地址…...

臻图信息以数字孪生技术推动智慧小区数字化建设
伴随着智慧城市建设进程的加速发展,加速传统小区的管理与服务向智能化升级转型。运用智慧化的管理和服务,利用信息技术和物联网等技术手段,将传统的居住区域与智能设备相结合,实现楼宇、社区设施、服务管理的数字化、网络化、智能…...

15.CSS发光按钮的悬停特效
效果 源码 <!DOCTYPE html> <html> <head><title>CSS Modern Button</title><link rel="stylesheet" type="text/css" href="style.css"> </head> <body><a href="#" style=&quo…...

MyBatis —— 动态SQL和缓存
前言 在上一篇文章中荔枝梳理了一些特殊的SQL查询和一对多、多对一的映射关系,而在这篇文章中荔枝将会梳理有关MyBatis动态SQL和MyBatis缓存的相关知识,同时也稍微了解了有关MyBatis中借助MAVEN中的插件管理来实现逆向工程。希望对需要的小伙伴有帮助哈哈…...
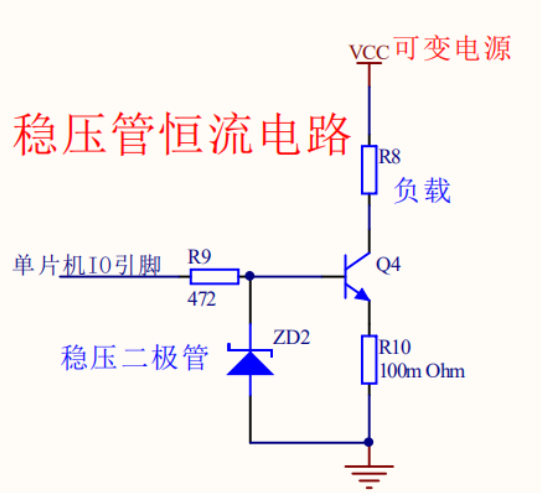
恒流电路的三种设计方案
作为硬件研发工程师相信对恒流电路不会陌生,本文介绍下三种恒流电路的原理图。 三极管恒流电路 三极管恒流电路 三极管的恒流电路,主要是利用Q2三极管的基级导通电压为0.6~0.7V这个特性;当Q2三极管导通,Q1三极管基级电压被拉低而…...

QT基础 关于QT延迟
目录 QT提供延时 1.自定义延时 2.使用QElapsedTimer 3.使用事件循环 4.跨平台延时 QT提供延时 这里提供四种方法: 1、多线程程序使用QThread::sleep()或者QThread::msleep()或QThread::usleep()或QThread::wait()进行延时处理。 Sleep不会释放对象锁&#x…...

LLM - LLaMA-2 获取文本向量并计算 Cos 相似度
目录 一.引言 二.获取文本向量 1.hidden_states 与 last_hidden_states ◆ hidden_states ◆ last_hidden_states 2.LLaMA-2 获取 hidden_states ◆ model config ◆ get Embedding 三.获取向量 Cos 相似度 1.向量选择 2.Cos 相似度 3.BERT-whitening 特征白化 …...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
